УДК 621.396.67

МНОГОМОДОВЫЕ АНТЕННЫ ДЛЯ СИСТЕМ ПОМЕХОПОДАВЛЕНИЯ

С. Е. Банков ¹, А. Г. Давыдов ², А. А. Курушин ³, К. Б. Папилов ², С. В. Самков ²

¹ИРЭ им. В.А. Котельникова РАН
²ОАО МКБ «Компас»
³НИУ МЭИ

Статья поступила в редакцию 30 ноября 2015 г.

Аннотация. Представлены результаты исследования многовходовых антенн с тремя собственными колебаниями, настроенными на одну частоту. Показана возможность подавления при помощи такой антенны помехи произвольной поляризации, приходящей с любого направления. Также показана возможность фазовой пеленгации. Получено условие оптимальной настройки многовходовой антенны. Рассмотрены собственные колебания круглой печатной антенны, предназначенной для применения в приемных системах с функциями помехоподавления и пеленгации. Исследование спектра собственных колебаний проводится при помощи приближенной резонаторной модели, позволяющей определять резонансные частоты, добротности и диаграммы направленности колебаний. Показано существование в исследуемой антенне осесимметричного колебания, обеспечивающего выполнение указанных функций в достаточно широкой полосе частот.

Ключевые слова: печатная антенна, многомодовая антенна, помехоподавление, фазовая пеленгация.

Abstract. Investigation and design of two multimode printed antennas – single and dual layered are considered. These antennas are intended for use in anti-jamming and direction finding systems. Proposed antennas are analyzed with help of an approximate resonator model. It is demonstrated numerically that these antennas may form radiation pattern with null in the required arbitrary direction for waves of both orthogonal polarizations. It is demonstrated with help of a numerical simulation that in the proposed antenna three dominant eigenmodes may be tuned to have identical resonance frequencies and Q-factors close to Q-factor of a conventional patch antenna. Application of three ports provides well matching and independent excitation of eigenmodes. Results of experimental investigation of dual layered printed antenna are presented.

Keywords: printed antenna, multimode antenna, anti-jamming, phase direction-finding.

Введение

Задачи помехоподавления и фазовой пеленгации в последнее время приобретают особую актуальность [1]. Обычно они решаются при помощи решеток, содержащих не менее трех, чаще всего печатных, антенн (ПА). Поскольку расстояние между ними выгодно выбирать близким к половине длины волны в свободном пространстве, то подобные системы имеют габаритные размеры, во многих случаях неприемлемые. Их уменьшение может быть достигнуто за счет применения ПА специального типа – многомодовых ПА (МПА) [2], [3], в которых одинаковые резонансные частоты имеют не менее трех собственных колебаний с ортогональными диаграммами направленности (ДН).

В квадратной и круглой ПА два основных колебания имеют одинаковые резонансные частоты. Их ДН можно назвать суммарными. Они имеют максимум вдоль оси антенны и отличаются поляризацией излучения. Для решения отмеченных выше задач необходимо на той же частоте возбудить в МПА третье колебание, имеющее симметричное относительно оси антенны поле и ДН разностного типа, с нулем вдоль оси МПА.

В данной работе рассматривается МПА круглой формы, изображенная на рис. 1. Целью нашего исследования было решение следующих задач: оценка возможности подавления помех и фазовой пеленгации при помощи МПА, оценка возможности одновременной настройки симметричного и несимметричных колебания на одну частоту, оценка добротности симметричного колебания и методов ее уменьшения.

Перечисленные задачи решались при помощи приближенной резонаторной модели [4], позволяющей дать качественную оценку исследуемой МПА при приемлемых временных затратах.

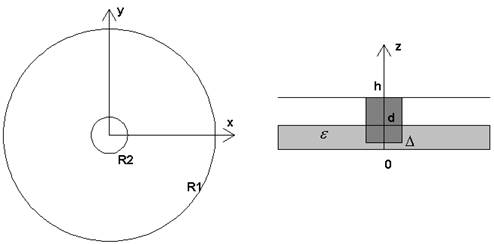
Рис. 1. Многомодовая антенна

1. Помехоподавление и фазовая пеленгация в системах с МПА

В рамках резонаторной модели поле излучения МПА приближенно заменялось полем кольцевых магнитных токов, текущих по металлическому экрану, на котором она расположена. Такая модель позволяет найти парциальные ДН собственных колебаний МПА. Токи I_φ, соответствующие симметричным колебаниям имеют зависимость от азимутального угла, описываемую функциями sinφ, cosφ. Токи симметричного колебания не зависят от азимутальной координаты.

Задача помехоподавления состоит в создании линейной комбинации парциальных ДН, имеющей нуль в заданном направлении, которое определяется углами φ₀,θ₀. Численно было показано, что МПА обеспечивает формирование нулей для двух направлений распространения волн в полупространстве над экраном. При этом для каждого из этих направлений нуль создается для волны одной поляризации. Возможно также подавление волн двух ортогональных поляризаций, но уже для одного сочетания углов φ₀,θ₀.

На рис. 2 показаны типичные нормированные ДН по двум компонентам поля, которые являются линейной комбинацией ДН МПА. Коэффициенты подбирались из условия формирования одного нуля для волн двух линейных поляризаций. Видно, что ДН для разных компонент поля имеют нули при заданном угле места θ₀=30⁰.

Рис. 2. Формирование нулей ДН МПА

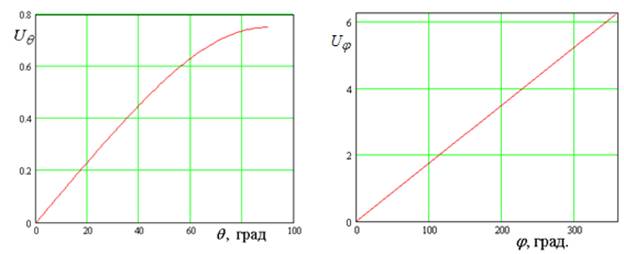
Фазовая пеленгация основана на измерении фаз с различных выходов антенной системы и формировании из них так называемой пеленгационной характеристики [5], которая представляет собой функцию углов падения волны, возбуждающей МПА.

а б

Рис. 3. Пеленгационные характеристики МПА

Типичная пеленгационная характеристика в угломестной плоскости U_θ показана на рис. 3 а. Она близка к линейной при сравнительно малых углах θ. При приеме волн, распространяющихся вдоль горизонта, линейность нарушается. Также показано, что данная характеристика зависит, хотя и незначительно, от угла φ. Пеленгационная характеристика в азимутальной плоскости U_φ весьма близка к идеальной (линейной), что видно из рис. 3 б.

Таким образом, мы можем сделать вывод, что МПА, в которой существуют три ортогональных собственных колебания решает задачу фазовой пеленгации. Также она может быть использована для подавления двух помех.

2. Исследование собственных колебаний МПА при помощи резонаторной модели

На первом этапе исследования собственных колебаний рассматривалась МПА со сплошным цилиндром без зазора (Δ=0). Расчеты показали, что в структуре существуют два симметричных колебания 1 и 2, отличающиеся структурой полей (кривые 1 и 2 на рис. 4 а). Предпочтительным является колебание 1, не имеющее вариаций поля по радиусу, так как его добротность излучения Q_r много меньше (см. рис. 4 б) добротности второго колебания. Причем при некоторых параметрах она может быть даже меньше добротности несимметричного колебания.

Интересно также, что симметричное колебание 1 может существовать в МПА без диэлектрического заполнения. При этом ее размеры существенно меньше размеров традиционной ПА без диэлектрика, настроенной на ту же частоту.

Недостатком МПА без зазора оказалась сложность одновременной настройки симметричных и несимметричных колебаний на одну частоту. На рис. 5 а,б показана зависимость толщины диэлектрика d от радиуса цилиндра R₂, обеспечивающая настройку МПА на частоту f=1.6 ГГц. Кривые 1 и 2 соответствуют симметричному и несимметричному колебаниям. Видно, что при Δ=0 (рис. 5 а) кривые 1 и 2 не имеют точек пересечения, а при Δ=0.6 они пересекаются в двух точках, что говорит о возможности настройки всех колебаний на одну частоту.

Рис. 4. Характеристики симметричных колебаний

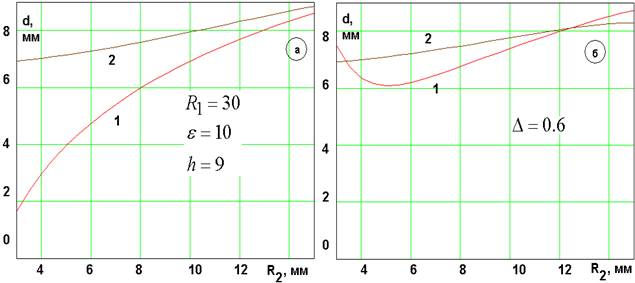
Рис. 5. Настройка колебаний МПА

Следует отметить, что наличие зазора ухудшает параметры симметричного колебания, в частности увеличивает его добротность. На рис. 6 показана зависимость радиационной добротности симметричного (кривая 1) и несимметричного колебаний (кривая 2) от радиуса R₂. Видно, что добротность симметричного колебания больше, чем у несимметричного, хотя и остается на приемлемом для многих приложений уровне.

Рис. 6. Добротность колебаний МПА

Наличие неоднородного диэлектрического заполнения не всегда удобно с конструктивной точки зрения. Поэтому в работе рассматривалась возможность создания МПА, заполненной средой с постоянной диэлектрической проницаемостью.

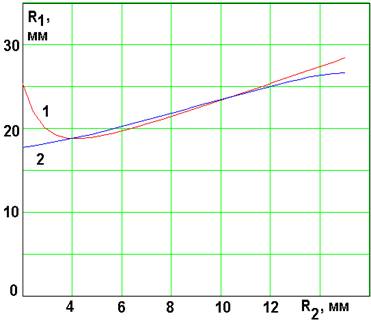
Рис. 7. Настройка МПА с однородной средой

Численные исследования показали, что настройка МПА со сплошным диэлектриком возможна за счет вариации ее размеров R₁, R₂, Δ. На рис. 7 показана зависимость радиуса R₁ от R₂ при настройке всех колебаний антенны на частоту f=1.6 ГГц, ε=10. Кривые 1 и 2, соответствующие симметричному и несимметричным колебаниям, имеют необходимые точки пересечения. Однако следует отметить, что при этом добротность симметричного колебания дополнительно возрастает по сравнению с другими рассмотренными случаями.

Таким образом, из исследования собственных колебаний можно сделать два важных вывода, определивших направления дальнейших исследований МПА. Первый вывод состоит в том, что в МПА без зазора и с воздушным заполнением существует низкодобротное осесимметричное колебание. В тоже время настроить его частоту на частоту несимметричного колебания невозможно. Для этого необходимо ввести диэлектрическое заполнение и зазор в между металлическим цилиндром и экраном. В этом случае добротность осесимметричного колебания существенно возрастает. Указанное противоречие не может быть разрешено при помощи одной конструкции. Поэтому для более детального исследования были выбраны два варианта МПА. Первый вариант - однослойная МПА, имеющая диэлектрическое заполнение и указанный зазор. Второй вариант - двухслойная МПА, в которой на одном слое расположена антенна с воздушным заполнением и зазором, в которой возбуждается только симметричное колебание. На другом слое располагается традиционная печатная антенна круглой формы, в которой возбуждаются два несимметричных колебания. Антенна по первому варианту имеет худшие электрические характеристики, по крайней мере, для симметричного колебания, но превосходит второй вариант МПА по габаритным показателям. Интерес к МПА по второму варианту обусловлен возможностью существенного расширения рабочего диапазона по каналу симметричного колебания.

3. Условия оптимальной настройки МПА

МПА имеет несколько входов и может рассматриваться как СВЧ многополюсник, который описывается матрицей рассеяния S. Важной практической задачей является настройка антенны, обеспечивающая максимальную энергетическую эффективность. Для антенны с одним входом условие такой настройки очевидно. Оно сводится к равенству нулю коэффициента отражения от единственного входа. При этом автоматически обеспечивается максимальная передача мощности с этого входа в свободное пространство и наоборот. При наличии нескольких входов, условие максимальной энергетической эффективности не столь очевидно.

МПА является неунитарным многополюсником, так как имеется излучение в свободное пространство. Поэтому физически реализуемой антенне может соответствовать нулевая матрица рассеяния

. (1)

Равенство нулю всех ее элементов означает, что входы антенны не только согласованы, но и развязаны. В общей теории антенных решеток [6] показано, что равенство (1) может быть выполнено только при условии ортогональности ДН, создаваемых решеткой. В нашем случае замена решетки на МПА не имеет существенного значения. Поэтому мы можем утверждать, что соотношение (1) выполняется, если ДН МПА ортогональны. Отметим, что равенство нулю матрицы рассеяния автоматически обеспечивает полную передачу мощности с любого входа антенны в свободное пространство, то есть является условием максимальной энергетической эффективности.

Ортогональность ДН МПА следует из ортогональности полей собственных колебаний. Поскольку антенна имеет осевую симметрию, то поле любого из колебаний можно представить в виде одной или нескольких азимутальных гармоник. Каждой такой гармонике соответствует зависимость от угла вида , где - номер азимутальной гармоники. Нетрудно убедиться, что осесимметричное колебание описывается полем нулевой гармоники с , а поля двух несимметричных колебаний соответствуют гармоникам с . Ортогональность полей собственных колебаний следует из ортогональности функций на интервале от нуля до . Поскольку зависимость поля излучения от угла повторяет аналогичную зависимость поля собственного колебания, то из их ортогональности следует ортогональность ДН.

В работе также показано, что соотношение (1), являющееся условием максимальной энергетической эффективности МПА, эквивалентно ее согласованию во всех режимах возбуждения собственных колебаний. Под таким режимом понимается возбуждение антенны при работе на передачу комбинацией падающих на ее входы волн U_in, n=1,2,3, которая возбуждает в МПА одно собственное колебание.

Если МПА возбуждается традиционным образом при помощи штыря, введенного внутрь антенны, то в круглой МПА с возбудителями расположенными через 120⁰, имеются три такие комбинации:

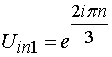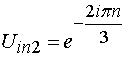, , . (2)

Нетрудно показать, что согласование в режимах (2) достигается при выполнении следующих двух равенств:

, (3)

Нетрудно увидеть, что условия (3) могут быть выполнены только при равенстве нулю элементов матрицы рассеяния S_11,12. Учитывая симметрию МПА нетрудно показать, что это эквивалентно обращению в нуль всей матрицы рассеяния МПА. Таким образом, мы видим, что согласование в режимах собственных колебаний эквивалентно условию (1). Однако в некоторых случаях применение равенств (3) оказывается более удобным, чем (1). Условия (3) использовались нами при электродинамическом моделировании МПА в качестве целевых функций оптимизации антенны.

3. Электродинамическое моделирование МПА

Для численного исследования были выбраны два варианта МПА: однослойная и двухслойная антенны. Конструкция однослойной МПА соответствует структуре на рис. 1 со сплошным диэлектрическим заполнением и конечным зазором Δ. Она показана на рис. 8. Двухслойная МПА на одном слое содержит традиционную круглую печатную антенну, а на другом слое антенну без зазора с воздушным заполнением.

Рис. 8. Однослойная МПА

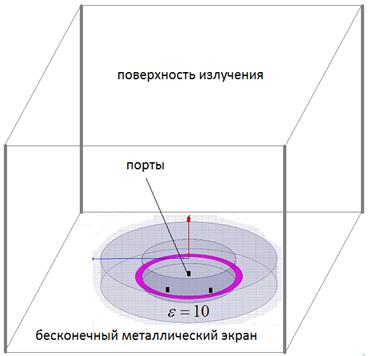
Рис. 9. Модель однослойной МПА для численного исследования

Электродинамическая модель МПА (см. рис. 9) имела ряд особенностей. Использовались источники возбуждения МПА в виде сосредоточенных портов с сопротивлением 50 Ом. Оказалось, что достижение согласования по двум критериям, сформулированным выше, затруднительно без использования дополнительных элементов. В качестве такого элемента использовалось металлическое кольцо и металлический цилиндр в центре МПА.

Целью численных экспериментов была настройка резонансных частот собственных колебаний на рабочую частоту МПА, равную 1.5 ГГц, а также согласование МПА по критериям (2).

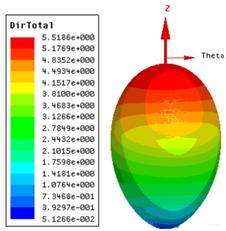
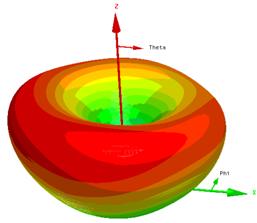
Рис. 10. ДН собственных колебаний МПА

На рис. 10,11 показаны результаты оптимизации МПА, выполненной из диэлектрика с диэлектрической проницаемостью 10. На рис. 10 показаны ДН собственных колебаний, а на рис. 11 частотные зависимости КСВ осесимметричного колебания (кривая 1) и колебания с круговой поляризацией (кривая 2).

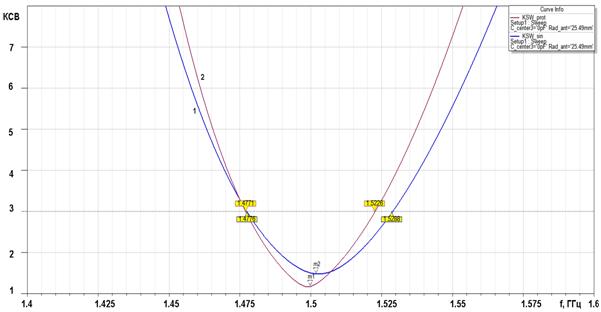
Рис. 11. КСВ МПА в разных режимах

Видно, что МПА хорошо согласована и имеет ДН требуемого вида.

В работе рассматривался ряд модификаций базового варианта МПА, изображенного на рис. 8, которые имеют улучшенные конструктивно-технологические характеристики. В частности, исследовалась возможность устранения зазора между углублением и нижним экраном с переносом портов в периферийную часть антенны. Исследование показало, что при этом затрудняется одновременная настройка резонансных частот всех трех собственных колебаний, а также повышается сложность обеспечения необходимых входных импедансов.

Исследовалась антенна с элементом возбуждения, расположенным в ее центре. Такое размещение порта весьма удобно, так как он селективно возбуждает осесимметричное собственное колебание и при этом не взаимодействует с несимметричными колебаниями, имеющим нули электрического поля в центре МПА. Недостатком центрального возбуждения МПА является сложность согласования, которое невозможно без применения внешних согласующих элементов: сосредоточенных или распределенных емкостей и индуктивностей, которые сужают полосу рабочих частот устройства и являются источником дополнительных тепловых потерь.

Рис. 12. Слой двухслойной МПА

Также в работе исследовалась антенна, показанная на рис. 12, которая является одним из двух слоев двухслойной МПА. В ней возбуждается осесимметричное колебание. Численные исследования полностью подтвердили полученный при помощи приближенной модели вывод о низкой добротности осесимметричного колебания. На рис. 13 показана полученная численно частотная зависимость КСВ антенны подтверждающая подтверждающая широкополосность антенны.

На рис. 14 показаны ДН в плосколсти вектора электрического поля двухслойной МПА, расположенной на бесконечном металлическом экране. Кривая 1 соответствует ДН осесимметричного колебания, а кривая 2 ДН несимметричного колебания.

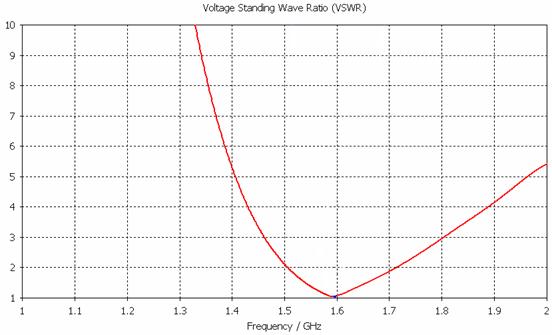
Рис. 13. КСВ двухслойной МПА

На рис. 15 показаны ДН двухслойной МПА в плоскости вектора магнитного поля. Кривые 1 и 2 соответствуют симметричному и несимметричному колебаниям. Видно, что ДН симметричного колебания практически не зависит от азимутального угла в отличие от ДН несимметричного колебания.

Рис. 14. ДН двухслойной МПА в Е – плоскости

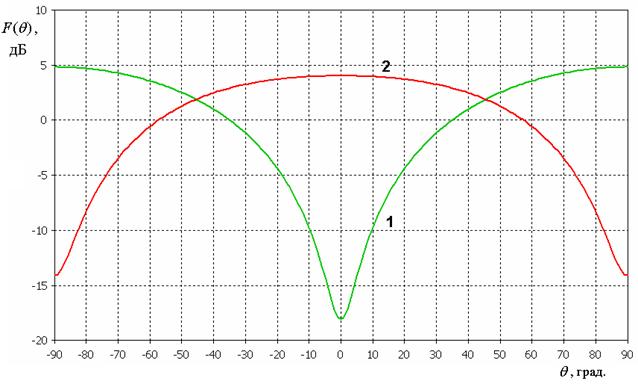
Рис. 15. ДН двухслойной МПА в Н – плоскости

4. Экспериментальное исследование двухслойной МПА

Экспериментально исследовалась двухслойная МПА, показанная на рис. 14. На нижнем слое располагается антенна с симметричным колебанием, а на верхнем слое антенна с двумя несимметричными колебаниями. Возбуждение симметричного колебания осуществляется в двух точках при помощи синфазного делителя мощности. Линии питания несимметричных колебаний проходят через металлический цилиндр нижнего слоя. Верхний слой возбуждается в двух точках. Антенна имеет три входа/выхода и располагается на экране размером 50х50 см.

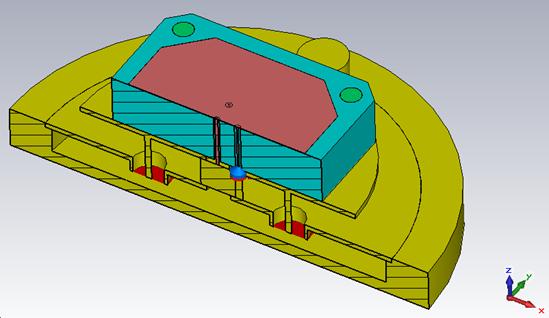
Рис. 16. Конструкция двухслойной МПА

На рис. 17,18 представлены некоторые экспериментальные результаты. На рис. 17 показана частотная зависимость КСВ. Кривая 1 соответствует симметричному, а кривая 2 несимметричному колебаниям.

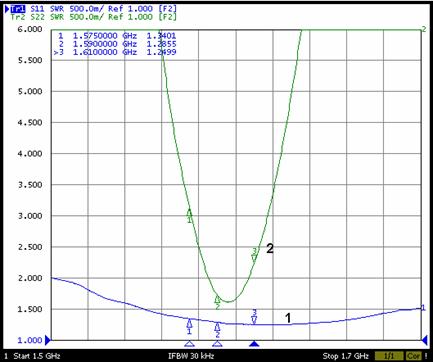
Рис. 17. Измеренный КСВ МПА

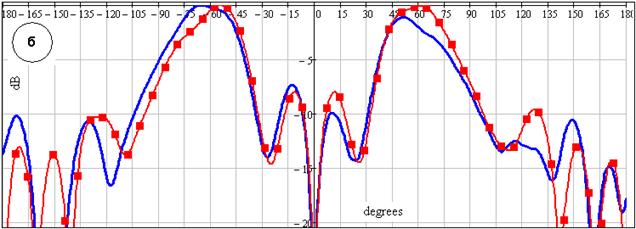
Рис. 18. Суммарная (а) и разностная (б) ДН

На рис. 18 а,б показаны ДН симметричного (а) и несимметричного (б) колебаний. Сплошной кривой даны измеренные, а точками рассчитанные ДН. Изрезанность ДН обусловлена влиянием экрана.

Литература

1. P. Misra and P. Enge. Global Positioning System: Signals, Measurements, and Performance. Ganga-Jamuna Press, Lincoln, MA, 2004.

2. Заявка на патент РФ «Малогабаритная антенна» № 2015136886 от 31.08.2015.

3. Заявка на патент РФ «Многомодовая печатная антенна» № 2015115055 от 22.04.2015.

4. Панченко Б.А., Нефедов Е.И. Микрополосковые антенны. М.: Радио и связь. 1986.

5. Денисов В.П., Дубинин Д.В. Фазовые пеленгаторы. Томск: Изд-во ТУСУР. 2002.

6. Сазонов Д.М. Многоэлементные антенные системы. М.: Радиотехника. 2015.