|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 1998 | |
А. В.
Корженевский, В. А. Черепенин
Институт радиотехники и
электроники РАН
Получена 25 ноября 1998 г.
Рассматриваются основы работы магнитоиндукционного томографа - устройства, позволяющего реконструировать распределение проводимости или диэлектрической проницаемости внутри объектов по результатам их зондирования переменным магнитным полем. Обсуждается физическая модель, требования к измерительной системе, методика решения обратной задачи и реконструирования изображений, возможные области применения индукционной томографии.
ВВЕДЕНИЕ
Компьютерная томография, основанная на использовании рентгеновского излучения, а также явления ядерного магнитного резонанса (ЯМР томография) широко используется в медицине и в промышленности. В основе компьютерной томографии (в широком смысле) лежит возможность математического реконструирования пространственного распределения той или иной характеристики вещества внутри объекта по влиянию этого вещества на физическое поле или излучение, пронизывающее объект и регистрируемое внешними датчиками [1].
В последнее время предлагаются новые методы томографии, основанные на использовании переменного электрического тока или электромагнитного поля в качестве зондирующего средства. Наибольшее развитие получила электроимпедансная томография или томография приложенных потенциалов [2, 10], заключающаяся в том, что через исследуемый объект, обладающий электрической проводимостью (в медицине это тело пациента), с помощью находящихся на его поверхности электродов пропускают слабый переменный электрический ток. С помощью других (иногда и тех же самых) электродов измеряются потенциалы на поверхности, возникающие при протекании тока через объект. Имея набор линейно независимых измерений, получаемых при различных комбинациях инжектирующих и измерительных электродов, можно реконструировать распределение электрического импеданса внутри объекта. Хотя предложено большое количество методов решения обратной задачи для этого случая, наиболее успешно в реально функционирующих устройствах работает метод обратного проецирования вдоль эквипотенциальных линий электрического поля, аналогичный применяемому в традиционной томографии. Применимость этого метода вытекает из возможности в линейном приближении связать относительные изменения разности потенциалов между смежными электродами с линейными интегралами относительного изменения импеданса вдоль эквипотенциалей, проходящих через эти электроды. Метод позволяет визуализировать только небольшие изменения проводимости внутри объекта и требует наличия опорного набора данных, соответствующих начальным значениям проводимости. Такая визуализация получила название динамической. В работах [3, 4] предложен модифицированный метод обратных проекций для электроимпедансной томографии, позволяющий получать изображения статических объектов в человеческом теле используя искусственный набор опорных данных, соответствующий телу с однородной проводимостью, и начать использование такого электроимпедансного томографа в медицинской практике [5]. Большие перспективы открывает использование в томографии высокочастотного магнитного поля и, в частности, его взаимодействия с проводящей средой, вызывающего появление вихревых токов. В работах [6, 7] предприняты попытки использования такого взаимодействия для визуализации проводимости, однако авторам, использовавшим по существу эмпирический подход, не удалось получить удовлетворительных результатов при восстановлении распределения электропроводности. Целью настоящей публикации является прояснение физических принципов, которые лежат в основе индукционной томографии, и формулирование на их основе подходов к реализации работоспособных устройств и алгоритмов реконструкции изображений.
1. ФИЗИЧЕСКАЯ МОДЕЛЬ И РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ
Пусть имеется источник и
приемник (измеритель) переменного магнитного
поля, разнесенные в пространстве. Например, это
могут быть два одинаковых индуктивно связанных
витка (см. рис. 1): один - индуктор, к
которому подключен источник переменного
напряжения 
с частотой w : 
, второй - детектор, к
которому подключен измеритель индуцируемой в
нем ЭДС. Электромагнитное поле в пространстве,
заполненном неоднородной средой, описывается
уравнениями Максвелла, которые в
рассматриваемом случае удобно записать в
следующем виде:
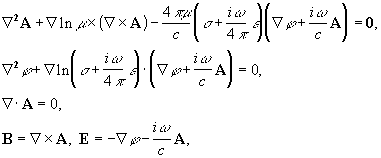(1)
где A и j - векторный и
скалярный потенциалы (используется Кулоновская
калибровка 
), E и B - напряженность электрического и
индукция магнитного полей, m и e - магнитная и диэлектрическая 
проницаемости,
s -
проводимость среды, c -
скорость света. Первое уравнение этой системы
соответствует уравнению Максвелла для 
,
второе - следствие уравнения непрерывности и
уравнения для 
. Граничные условия для
уравнений (1) вытекают из равенства нулю
нормальной компоненты тока проводимости на
границе объекта: 
, где n - единичный вектор, нормальный к
поверхности объекта. Если предположить, что
влияние среды приводит к малому изменению поля
индуктора, задаваемого векторным потенциалом 
,
и m =1, то
систему (1) можно приближенно заменить
уравнением:
, (2)
которое описывает магнитное
поле, создаваемое индуцированными токами и
токами смещения в среде, возникающими под
действием переменного магнитного поля
индуктора. Из уравнения (2) видно, что
индуцированный ток, обусловленный проводимостью
среды, вносит вклад в квадратуру магнитного поля
сдвинутую на 
относительно поля
индуктора (в мнимую часть поля), а ток смещения,
пропорциональный диэлектрической
проницаемости, - в синфазную квадратуру
(действительную часть). Таким образом, измеряя
обе квадратуры сигнала детектора, можно
независимо определять интегральную
проводимость и диэлектрическую проницаемость
среды, причем задача определения проводимости
оказывается облегченной тем, что в отсутствии
среды измеряемая квадратура равна нулю и
точность измерения определяется абсолютной
точностью регистратора, в то время как для
определения диэлектрической проницаемости
требуется измерять малые изменения синфазной
квадратуры на фоне мощного сигнала индуктора и
точность таких измерений значительно ниже.
Становятся ясными и трудности, с которыми
столкнулись авторы [6, 7] при
попытках визуализировать распределение
электропроводности по результатам измерений
полной амплитуды магнитного поля, поскольку в
линейном приближении проводящая среда влияет
только на фазу регистрируемого поля. Уравнение (2)
может быть использовано для приближенного
решения обратной задачи реконструкции
изображений, однако с практической точки зрения
более эффективным представляется способ,
основанный на рассмотрении системы в
квазистатическом приближении с использованием
эквивалентных схем.
В квазистатическом приближении
(
, l - расстояние между витками) в
свободном пространстве систему можно
рассматривать как бесжелезный трансформатор. В
индукторе течет ток 
, отстающий на 
от напряжения 
, в детекторе ток
отсутствует (предполагается, что измеритель
имеет бесконечное входное сопротивление). При
отсутствии проводящих объектов в окружающем
пространстве и пренебрежении активным
сопротивлением индуктора и током смещения
измеритель регистрирует напряжение 
,
синфазное с амплитудой 
, где 
- индуктивность витка, 
- коэффициент
взаимной индукции витков. Индуктивная связь
означает, что часть магнитного потока,
создаваемого индуктором, пронизывает виток
детектора, создавая в нем ЭДС индукции. Таким
образом, индуктор и детектор связаны между собой
только линиями магнитного поля B, проходящими через оба витка. Эти
линии в пространстве между витками локализованы
в пучок, диаметр которого не превышает диаметра
витка (рис. 1). Если внести теперь в
пространство между витками небольшой
слабопроводящий или магнитный объект, то
магнитное поле изменится благодаря
возникновению индуцированных токов и токов
смещения в объекте или его намагничиванию. Если
бы геометрия магнитного поля при этом
сохранялась, то сигнал детектора изменялся бы
только при пересечении предметом этого узкого
пучка линий магнитного поля (общего магнитного
потока двух витков). Изменение будет тем большим,
чем больше протяженность объекта вдоль этого
пучка. Возникает аналогия с рентгеновской
томографией с заменой прямолинейного пучка
рентгеновского излучения на криволинейный пучок
силовых линий. К сожалению, ситуация в случае
квазистатического электромагнитного поля
существенно отличается от ситуации с
коротковолновым излучением. Из уравнения 
следует, что невозможно изменить магнитное поле
в локальном пучке силовых линий не изменяя
геометрию и величину поля в окружающем этот
пучок пространстве. Таким образом, предмет будет
изменять поле как внутри, так и вне пучка, который
он пересекает, предмет находящийся вне пучка,
связывающего детектор с индуктором, будет влиять
на сигнал детектора. Тем не менее, аналогия с
рентгеновской томографией все же не лишена
смысла, так как можно показать, что область
наибольшей чувствительности для каждой
регистрирующей катушки совпадает с пучком
силовых линий, связывающих эту катушку с
индуктором, а нелокальность взаимодействия
объекта и поля лишь ограничивает разрешающую
способность системы. Для того чтобы
иметь возможность обратного проецирования вдоль
невозмущенных силовых линий магнитного поля,
необходимо, чтобы возмущения, вносимые
исследуемой средой, были малыми. То есть
измерения должны проводиться в условиях слабого
скин-эффекта: 
, 
- толщина скин слоя для магнитного
поля в исследуемой среде. С другой стороны среда
все же должна оказывать на магнитное поле
влияние, достаточное для регистрации детектором.
Эти условия, являются критерием для выбора
рабочей частоты томографа 
. В отличие
от электроимпедансного томографа, здесь можно
выбором частоты обеспечить справедливость
линейного приближения не только при
реконструкции малых изменений проводимости
объекта, но и абсолютных значений этой
проводимости. Кроме того, отсутствие
необходимости размещения контактов на
поверхности тела, форма которого заранее
неизвестна, позволяет с высокой точностью
провести начальные (опорные) измерения при
отсутствии объекта. Важным отличием
индукционного томографа является также то, что
зоны наибольшей чувствительности для него
представляют собой трехмерные области -
"трубки", связывающие индуктор и детектор,
тогда как в электроимпедансном томографе эти
области представляют собой пространство между
двумя бесконечными поверхностями -
эквипотенциалями электрического поля. Поэтому
для индукционного томографа влияние объектов,
располагающихся вне плоскости исследования,
должно быть слабее чем для электроимпедансного.
Рассмотрим эквивалентную схему
системы, включающей индуктор 
,
подключенный к источнику напряжения, детектор 
и слабопроводящий объект, расположенный между
ними, см. рис. 2. Моделью объекта здесь
является обмотка трансформатора 
,
нагруженная на параллельно включенные активное
сопротивление 
(условие слабого
скин-эффекта) и емкость 
(предполагается, что ток смещения в объекте не
превышает тока проводимости). Воспользовавшись
правилами Кирхгоффа для гармонических токов,
запишем уравнения для комплексных амплитуд
напряжений и токов в схеме:
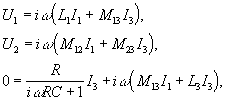(3)
где 
-напряжения и токи в
обмотках, 
- коэффициенты само и
взаимоиндукции, см. рис. 2. Из системы
уравнений (3), пренебрегая членами выше первого
порядка относительно малого параметра 
и 
, получим соотношение между током в
индукторе и напряжением на детекторе:
(4)
и между напряжениями на индукторе и детекторе:
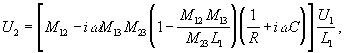(5)
Из (4) и (5) можно сделать два
важных вывода. Первый - в линейном приближении,
как и следовало из уравнения (2), амплитуда
сигнала детектора не зависит от проводимости, но
зависит от диэлектрической проницаемости
объекта. Влияние проводящего объекта
проявляется в изменении фазы регистрируемого
сигнала (появлении малой квадратурной
компоненты сигнала детектора синфазной току в
индукторе или сдвинутой на 
относительно напряжения на индукторе). Измерение
фазового сдвига, которое сводится к измерению
интервалов времени и может быть легко выполнено
с высокой точностью, предпочтительнее измерения
квадратурных амплитуд сигнала, требующего
трудоемких и неточных преобразований напряжение
- код. Второй вывод - целесообразно
регистрировать изменение фазы сигнала детектора
относительно фазы тока в индукторе, а не
относительно напряжения на индукторе. В
последнем случае изменение фазы меньше и
результат измерения сильно зависит от объектов,
находящихся вблизи индуктора и не обязательно
расположенных в зоне чувствительности
детектора. Использование таких фазовых
измерений позволяет, кроме того, уменьшить
влияние паразитных емкостных связей а также
высокой диэлектрической проницаемости объекта,
поскольку эти факторы влияют в существенно
большей степени на амплитуду сигнала детектора
чем на его фазу.
Итак, пусть сдвиг фаз между
током в индукторе и напряжением на детекторе
равен 
. Считая 
, что всегда можно
обеспечить соответствующим выбором частоты , из (4) в
линейном приближении получаем:
. (6)
Определим теперь связь между
входящими в это выражение параметрами и
характеристиками пробного объекта. Пусть объект
имеет протяженность dl,
вдоль магнитного поля, а в поперечном
направлении целиком пересекает общий магнитный
поток индуктора и детектора. Величина
сопротивления R для
вихревого тока, индуцируемого магнитным полем,
обратно пропорциональна сечению через которое
протекает ток и удельной проводимости объекта 
.
Таким образом, выражение (6) можем записать в
следующем виде:
, (7)
где W -
геометрический весовой фактор, зависящий от
взаимного расположения индуктора, объекта и
детектора. Емкость C для
пробного объекта можно оценить исходя из тех же
геометрических соображений как 
, что можно
использовать при реконструкции диэлектрической
проницаемости по результатам измерений
синфазной с индуктором квадратуры сигнала
детектора. Для протяженной среды после
интегрирования (7) вдоль линии магнитного поля,
связывающей индуктор и детектор, получим, что
измеряемый фазовый сдвиг 
равен
линейному интегралу взвешенной проводимости.
Имея набор таких интегралов для всех индукторов
и детекторов, расположенных вдоль замкнутого
контура вокруг исследуемого объекта, можно
реконструировать распределение взвешенной
проводимости в сечении среды (произвести
обращение). В процессе реконструирования можно
производить взвешивание с коэффициентом 
и получить в результате распределение
проводимости 
. Конечно, использованные
при выводе (7) соображения имеют приближенный
характер. Достаточно сказать что весовой фактор W,
вообще говоря, зависит и от
поперечных размеров тестового объекта, даже если
они превосходят поперечное сечение общего
магнитного потока индуктора и детектора. Однако
полученные соотношения и выводы вполне
достаточны для практической реализации
индукционного томографа и создания
работоспособного алгоритма реконструкции
проводимости.
2. ИЗМЕРИТЕЛЬНАЯ СИСТЕМА ИНДУКЦИОННОГО ТОМОГРАФА
Для получения данных, требуемых для реконструкции изображения, томограф должен содержать набор индукторов и детекторов, расположенных в плоскости исследования. Простейшей конфигурацией является расположение передающих и приемных катушек по окружности вокруг объекта, рис. 3а. Хотя в качестве индукторов и детекторов можно использовать по очереди одни и те же катушки, использование специализированных катушек существенно облегчает проблемы коммутации, обеспечивает необходимое электрическое согласование, поскольку количество витков в приемных и передающих катушках в этом случае может быть разным. В процессе измерений активизируется один из индукторов и снимаются показания всех детекторов. Эта процедура повторяется для всех индукторов. Начальные значения набегов фаз, обусловленные задержками при обработке сигнала, влиянием элементов конструкции, находящихся в поле индукторов, и т.п., измеряются при отсутствии объекта в рабочей области томографа и запоминаются. Начальные значения фазовых сдвигов могут быть также измерены или вычислены для случая заполнения исследуемого пространства однородной или неоднородной проводящей средой с целью повышения качества визуализации за счет компенсации влияния фоновой проводимости или получения динамических томограмм (визуализации изменений проводимости). Поскольку линии магнитного поля продолжаются по обе стороны от плоскости индуктора, для исключения влияния окружающих предметов система индукторов и детекторов должна быть окружена экраном. На низких частотах (до нескольких мегагерц) наиболее подходящим представляется ферромагнитный экран, через который замыкаются линии магнитного поля индуктора. На более высоких частотах более простым и эффективным является проводящий электромагнитный экран. Для хороших проводников на частотах порядка 10 МГц толщина скин слоя составляет около десяти микрон, т.е. поле практически не проникает в экран и его линии, изгибаясь, проходят вдоль поверхности экрана. Исходя из выводов раздела 1 и данных об электропроводности тканей человеческого тела [2], рабочую частоту медицинского индукционного томографа следует выбрать в диапазоне 10 - 20 МГц. Для других вероятных областей применения индукционной томографии (геологоразведка, неразрушающий контроль) рабочая частота будет ниже.
Используя несколько контуров с катушками, расположенных один над другим, можно, одновременно проведя измерения для нескольких сечений, получить трехмерное распределение проводимости. Для многих задач окажется полезной система с линейным расположением индукторов и детекторов, рис. 3б. Здесь также измеряются линейные интегралы взвешенной проводимости вдоль линий магнитного поля, связывающих индуктор с детекторами. В отличие от электроимпедансного томографа с такой геометрией, который рассматривался, например, в [8], при магнитоиндукционном методе снимается вырождение по плоскостям, проходящим через линию индукторов-детекторов, и томограф обеспечивает визуализацию проводимости в срезе среды, перпендикулярном плоскости катушек. Глубина визуализации при этом составляет примерно половину длины измерительной линейки. Используя несколько линеек (матрицу из катушек) можно реконструировать трехмерное распределение проводимости под поверхностью.
РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЙ
Фазовые сдвиги, измеренные аппаратной частью томографа, представляют собой в линейном приближении интегралы от взвешенной проводимости вдоль линий магнитного поля, связывающих индуктор с детекторами. При наличии набора таких данных, полученных для всех индукторов, расположенных по замкнутому контуру вокруг объекта, для реконструкции проводимости в сечении объекта может быть использован метод свертки и обратной проекции [1]. Этот метод широко используется в электроимпедансной томографии [9], однако поскольку для индукционной томографии, как видно из (1) и (2), регистрируемые данные соответствуют распределению проводимости, а не ее градиента, как в электроимпедансной томографии, при реконструировании не может быть пропущен этап свертки (фильтрации данных фильтром с линейно нарастающей пространственно-частотной характеристикой).
Процедура обратного проецирования с взвешиванием для томографа с полярной геометрией может быть формально описана с помощью следующего соотношения:
, (8)
где - проводимость среды
в точке с полярными координатами 
; 
- полярный
угол индуктора (индукторы и детекторы
располагаются на окружности с радиусом равным 1); 
- параметрические уравнения линии магнитного
поля для индуктора с 
, проходящей через
заданную точку 
, s - расстояние вдоль
линии от этой точки до текущей точки на линии,
увеличение s соответствует
движению от индуктора; N -
калибровочный коэффициент, 
-
результат свертки измеренных
фазовых сдвигов 
с фильтрующей функцией,
соответствующей, например, фильтру Рамачандрана
– Ликшинарайана. Поскольку реально детекторы
расположены в фиксированных точках с дискретным
шагом, эта величина вычисляется путем линейной
интерполяции показаний двух ближайших к
требуемой точке детекторов. Весовой коэффициент W
определим из условия, что
величина
для одного и того же малого
пробного объекта не должна зависеть от его
координат. Для упрощения выкладок при
определении весового фактора можно
аппроксимировать индуктор и детектор точечными
диполями, а тестовый объект - совокупностью
диполей, распределенных вдоль линии
перпендикулярной плоскости визуализации, причем
дипольный момент каждого из этих диполей
пропорционален величине магнитного поля
индуктора в точке расположения диполя и
направлен вдоль этого поля. В выражении (8)
использовано свойство центральной симметрии
системы при расположении индукторов и
детекторов вдоль окружности, охватывающей
объект. При этом значения W и линии магнитного поля вычисляются
только для одного из индукторов, а переход к
любому другому индуктору осуществляется путем
поворота системы координат на соответствующий
угол.
Выбором рабочей частоты томографа можно обеспечить справедливость линейных приближений, используемых при реконструкции изображений, однако в некоторых случаях для повышения точности может потребоваться учет нелинейности, связанной с изменением геометрии линий магнитного поля в присутствии объекта. Реконструкция изображения при этом может проводиться путем последовательных итераций с коррекцией магнитного поля на очередной итерации по результатам реконструкции проводимости на предыдущей итерации. Альтернативным подходом к реконструкции изображения в индукционной томографии может быть использование метода обращения, основанного на разложении искомого распределения проводимости по ортогональной системе базисных распределений с той или иной процедурой вычисления коэффициентов этого разложения, обеспечивающей минимизацию отличий результатов решения прямой задачи (уравнений (1) или (2) для индукционной томографии) от данных реальных измерений.
Для иллюстрации возможность
получения томографических изображений методом
индукционной томографии, проведено
моделирование результатов измерений томографа с
32 индукторами и детекторами, расположенными по
окружности, для объекта, распределение
проводимости в сечении которого показано на рис. 4а. Это распределение условно
моделирует сечение грудной клетки человека.
Прямой задаче для индукционной томографии в
линейном приближении соответствует уравнение (2),
которое в случае свободного пространства можно
решать используя функцию Грина - формулу
Био-Савара-Лапласа, в которой плотность тока
определяется правой частью уравнения (2).
Используя в качестве 
векторный потенциал
магнитного диполя, которым аппроксимируется
индуктор, и считая 
, для амплитуды
возмущения магнитного поля 
,
создаваемого проводящим объектом, получим:
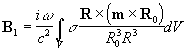
где m -
амплитуда магнитного момента индуктора, 
- радиус-вектор от индуктора в dV , R - радиус-вектор из dV в точку наблюдения. Вычисленные
возмущения определяют сдвиги фаз сигналов,
регистрируемых детекторами, которые
использовались как исходные данные для
реконструкции проводимости методом свертки и
обратного проецирования. Для качественного
реконструирования внутренней структуры
протяженных проводящих объектов с относительно
небольшой внутренней вариацией проводимости,
таких как человеческое тело, необходимо в
качестве начальных использовать сдвиги фаз,
соответствующие телу с однородной
проводимостью, не слишком отличающейся от
средней проводимости исследуемого тела. Иначе
общие большие фазовые набеги, создаваемые телом,
маскируют малые вариации, обусловленные его
внутренней структурой. Результат
реконструирования представлен на рис. 4б.
ЗАКЛЮЧЕНИЕ
Индукционная томография позволяет независимо визуализировать распределение проводимости и диэлектрической проницаемости в неоднородной среде. При этом томограф с регистрацией фазового сдвига между током в индукторе и напряжением на детекторе позволяет с высокой точностью визуализировать распределение абсолютной электропроводности внутри различных объектов при относительно несложной регистрирующей аппаратуре. Как и прочие низкочастотные электромагнитные системы, индукционный томограф не может иметь высокую разрешающую способность, однако он обладает рядом важных достоинств. Важным преимуществом по сравнению с электроимпедансной томографией является возможность визуализации статического распределения электропроводности с высокой точностью благодаря фиксированному расположению индукторов и детекторов в пространстве, а также возможности регулирования степени нелинейности связи между электропроводностью среды и электромагнитным полем на периферии объекта путем выбора частоты магнитного поля. Существенным является тот факт, что слабопроводящие оболочки прозрачны для магнитного поля, что позволяет, например, исследовать распределение и изменения импеданса в головном мозге взрослых людей. Бесконтактность и безвредность исследования, возможность выбором частоты регулировать "проницающую способность" магнитного поля открывает широкие перспективы для применения индукционной томографии не только в медицине, но и в системах безопасности, таможенном контроле, геофизике, промышленности.
Рис. 1. Элементы измерительной системы индукционного томографа.
Рис. 2. Эквивалентная схема входных цепей индукционного томографа.
(а)
(б)
Рис. 3. Измерительная система индукционного томографа с цилиндрической (а) и линейной (б) геометрией (1 - катушки индукторов и детекторов, 2 - экран).
Рис. 4. Исходное распределение электропроводности, моделирующее сечение грудной клетки человека, (а) и его визуализация индукционным томографом (б). Изображение реконструировано методом обратного проецирования на основе расчетных значений фазовых сдвигов. Области, обозначенные на рисунке (а), соответствуют: 1 - скелетные мышцы (0,1 См/м), 2 - позвоночник (0,007 См/м), 3 - легкие (0,05 См/м), 4 - сердце (0,5 См/м).
СПИСОК ЛИТЕРАТУРЫ
1. Наттерер Ф. Математические аспекты компьютерной томографии. М.: Мир, 1990.
2. Barber D. C., Brown B. H.//J. Phys. E: Sci. Instrum. 1984. V. 17. № 9. P. 723.
3. Korjenevsky A. V.//Proc. IX Int. Conf. Electrical Bio-Impedance. Heidelberg, Germany, 1995. P. 532.
4. Cherepenin V. A., Korjenevsky A. V., Kornienko V. N. et al.//Proc. IX Int. Conf. Electrical Bio-Impedance. Heidelberg, Germany, 1995. P. 430.
5. Shinkarenko V., Kostromina E.//Proc. IX Int. Conf. Electrical Bio-Impedance. Heidelberg, Germany, 1995. P. 476.
6. Yu Z.Z., Peyton A.J., Conway W.F. et al.//Electronic Letters. 1993. V.29. № 7. P.625.
7. Al-Zeibak S., Goss D., Lyon G. et al.//Proc. IX Int. Conf. Electrical Bio-Impedance. Heidelberg, Germany, 1995. P. 426.
8. Powell H.M., Barber D.C., Freeston I.L.//Clin. Phys. Physiol. Meas. 1987. V. 8, Suppl. A. P. 109
9. Barber D.C. and Seagar A.D.//Clin. Phys. Physiol. Meas. 1987. V. 8, Suppl. A. P. 47
10. Electromagnetic Tomography - домашняя страница на сервере ИРЭ РАН
Авторы:
Корженевский Александр Владимирович, e-mail: sasha@cplire.ru
Черепенин Владимир Алексеевич, e-mail: cher@cplire.ru
 |
 |