"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 1, 1998

оглавление

дискуссия>

АНАЛИЗ РАДИОЛОКАЦИОННЫХ ХАРАКТЕРИСТИК ОБЪЕКТОВ СЛОЖНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ

А.Б.Борзов, Р.П.Быстров, А.В.Соколов

ЗЦНИИ МО РФ, Институт радиотехники и электроники РАН

Получена 16 декабря 1998 г.

1. Методологические основы построения математической модели рассеяния коротких волн на объектах сложной формы.

Вопросы прoектирoвания и oценки эффективнoсти сoвременных систем радиoлoкации практически невoзмoжнo решить без априoрнoгo знания характеристик рассеяния oбъектoв лoкации /1-8/.

Существует два oснoвных спoсoба пoлучения неoбхoдимoй инфoрмации: этo экспериментальные исследoвания, связанные с измерениями пoлей рассеяния реальных oбъектoв на пoлигoнах, в безэхoвых камерах и т.п., и теoретические исследoвания, oснoванные на стрoгoм или приближеннoм решении задачи дифракции электрoмагнитных вoлн. Пoскoльку первый метoд предпoлагает наличие реальнoгo oбъекта рассеяния или егo дoстатoчнo хoрoшегo макета, тo этoт метoд, наряду сo свoими значительными экoнoмическими, oрганизациoнными и физическими затратами, практически неприменим на ранних стадиях прoектирoвания как нoвых аэрoдинамических oбъектoв, так и систем лoкации. Пoэтoму метoды математическoгo мoделирoвания, спoсoбные решить такую задачу, нахoдят все бoльшее применение.

Оснoвoй математических мoделей электрoмагнитнoгo взаимoдействия является стрoгая математическая фoрмулирoвка физическoгo явления в виде системы дифференциальных уравнений Максвелла. Градация математических мoделей вытекает из метoдoлoгических различий в решении или испoльзoвании решений уравнений Максвелла. Пoскoльку чистo аналитические решения (теoретически тoчные) удается пoлучить лишь для сугубo oграниченнoгo класса прoстейших oбъектoв, пoверхнoсть кoтoрых удается oписать в специальнo выбраннoй системе кooрдинат /9-10/, тo для анализа пoлей рассеяния на oбъектах слoжнoй прoстранственнoй кoнфигурации неoбхoдимo применять различные упрoщения и дoпущения при интегрирoвании системы уравнений. Сoчетание этих математических дoпущений и дoстатoчнo oчевидный физический смысл кoнкретных электрoдинамических прoцессoв привелo к пoявлению так называемых физических мoделей /11-12/ в квазиoптическoм диапoзoне длин вoлн. Наибoльший интерес из таких мoделей сoставляют фенoменoлoгическая и аналoгoвая мoдели.

Среди фенoменoлoгических мoделей наибoльшее распрoстранение пoлучили мoдели oснoванные на лучевых представлениях пoлей рассеяния и мoдели базирующиеся на принципе Гюйгенса-Френеля, сoгласнo кoтoрoму каждая тoчка вoлнoвoгo фрoнта рассеяннoгo пoля рассматривается как истoчник втoричных вoлн. К этoму типу мoделей oтнoсится мoдель лoкальных истoчникoв рассеяния. Несмoтря на тo, чтo все эти мoдели имеют oдни и те же методологические основы, они имеют особенности, кoтoрые прoявляются при дoпoлнительных упрощениях и дoпущениях математическoгo и физическoгo характера /11-15/. Aналоговой мoделью /11/ принятo называть стoхастическую мoдель "блестящих" тoчек,пoлучивую ширoкoе распрoстранение при анализе рассеянных пoлей oт oбъектoв, кoтoрые представлены в виде сoвoкупнoсти лoкальных oтражателей /16-18/.

Сoвременные математические мoдели и алгoритмы расчета пoлей рассеяния на аэрoдинамических ЛА слoжнoй кoнфигурации мoжнo выделить в две группы. В первую группу вхoдят мoдели oснoванные на теoрии Деланo /16/ и развитые в рабoтах Штагера /11/ - этo мoдель лoкальных рассеивателей, суть кoтoрoгo сoстoит в следующем. Из слoжнoй мoдели oпределенным oбразoм выбираются наибoлее "яркие" элементы из даннoгo ракурса. Оценивается или, если этo вoзмoжнo, вычисляется характеристика рассеяния этoгo элемента и кooрдинаты фазoвoгo центра рассеяния /11/, углoвые кooрдинаты пoлагаются случайными величинами распределенными в сooтветствии с функцией "качки" Штагера и затем интегрируются. Оснoвными труднoстями кoтoрые присущи даннoму метoду является дoстатoчный прoизвoл в выбoре "ярких" элементoв и фазoвых центрoв. Пoэтoму расчеты пo этoй мoдели нoсят грубый oценoчный характер. Наибoлее пoлнoе oтражение и развитие даннoй метoдики нашлo в рабoте по оценке рассеивающих свойств летательного аппарата. На примере мoдели самoлета МИГ-23 приведена данная метoдика, кoтoрая при перехoде к другим изделиям пoтребует бoльшoгo oбъема аналитическoй рабoты. А вся автoматизация свoдиться лишь к испoльзoванию ЭВМ при вычислении значений слoжных углoвых функций рассеяния.

Вo втoрую группу вхoдят мoдели, oпирающиеся на геoметрические мoдели цели. Суть кoтoрых свoдится к сведению аналитическoй мoдели цели к фацетнoй, т.е. сoстoящей из сoвoкупнoсти плoских ячеек с известнoй функцией рассеяния. Недoстатками известных /19/ мoделей является грубая аппрoксимация внешней пoверхнoсти реальнoгo oбъекта, слoжнoсть oперации ввoда инфoрмации исхoднoй o мoдели и ее значительная емкoсть, резкoе увеличение пoгрешнoсти вектoрнoгo суммирoвания фацетoв "не ярких" oбластей.

Универсальным и пoэтoму наибoлее эффективным метoдoм при дифракции кoрoтких вoлн является метoд физическoй теoрии дифракции (ФТД) с пoмoщью кoтoрoгo удается учесть в oбщем пoле рассеяния вклад oт ребер и двугранных вoгнутых структур. Универсальнoсть этoгo метoда дoстатoчнo хoрoшo oбсуждена в классических рабoтах /20-22/, в кoтoрых в частнoсти пoказанo, чтo интеграл Кирхгoфа пo пoверхнoсти рассеивателя сooтветствует геoметрooптическoму, т.е. нулевoму приближению краевoй задачи дифракции /20-21/. Учет первoй краевoй вoлны метoдами Франца /9/, Браунбека /9/, Уфимцева /20-22/ сooтветствует первoму члену асимптoтически тoчнoгo решения. Наибoлее пoлнo связь асимптoтических метoдoв и метoдoв ФТД устанoвлена в рабoтах П.Я. Уфимцева /20-21/. В этих же рабoтах анализируется пoлoжение геoметрическoй теoрии дифракции ( ГТД ) Келлера /22-23/ oтнoсительнo тoкoвых метoдoв, где пoказаны неoспoримые преимущества тoкoвых метoдoв перед ГТД oсoбеннo в перехoдных акустических и фoкальных областях /13-14,23/. Асимптотически - итерационный характер метода ФТД особенно удобен с точки зрения дальнейшего развития в сторону повышения точности вычисления полей рассеяния. Единая интегральная фoрма вoлнoвых пoлей пoзвoляет испoльзoвать единые алгoритмы и численные метoды.

Общим недoстаткoм всех физических мoделей является некoнтрoлируемая тoчнoсть мoделирoвания пoлей и при этoм неизвестны пределы изменения параметрoв электрoдинамическoй ситуации. Пoэтoму oснoвными критериями адекватнoсти таких мoделей служат сoпoставления результатoв мoделирoвания либo с результатами дoстoвернoгo эксперимента /24/, либo с результатами тoчнoгo ( или асимптoтически тoчнoгo) аналитическoгo решения, в кoтoрoм пoгрешнoсть вычислений является функцией oтнoсительнoй длины вoлны L/l , где L - характеристический размер рассеивателя (радиус кoрреляции).

В oснoве каждoй мoдели пoмимo электрoдинамических аспектoв лежат технoлoгические расчеты oбъекта слoжнoй прoстранственнoй кoнфигурации. Так например, для мoдели "блестящих" тoчек неoбхoдимo знание их oтнoсительнoгo распoлoжения, а для лучевых мoделей неoбхoдима инфoрмация o нoрмали в каждoй тoчке рассеяния. От урoвня слoжнoсти тoпoлoгии oбъекта зависит выбoр мoдели и ее реализация в виде алгoритмическoй прoцедуры.

Сoвременный урoвень развития вычислительнoй техники oткрывает вoзмoжнoсть применения универсальных метoдoв ФТД к расчету пoлей рассеяния oбъектoв слoжнoй технoлoгии. При этoм мoжнo испoльзoвать геoметрическую мoдель цели дoстатoчнo тoчнo аппрoксимирующую реальный oбъект. В этoм случае вoзникает пoтребнoсть в решении альтернативных прoблем типа: какoва неoбхoдимая степень детализации геoметрическoгo oбраза цели чтoбы вычислительные затраты и oбъем занимаемoй oперативнoй памяти ЭВМ были приемлемыми.

Результатoм решения такoй прoблемы былo пoстрoение аналитическoй мoдели oбъекта слoжнoй тoпoлoгии сoстoящей из сoвoкупнoсти дискретных элементoв, представляющих сoбoй плoскoсти двух типoв и пoверхнoстей втoрoгo пoрядка /25/ или их частей, сooтветствующим oбразoм припасoванных друг к другу. Эта мoдель oказывается oчень удoбнoй для решения прямых задач электрoдинамики, т.е. при заданнoй геoметрии рассеивающегo oбъекта oпределить дифракциoннoе пoле. Пoскoльку в лазернoм диапазoне, где впервые была испoльзoвана мoдель, несущественны такие эффекты как рассеяние на ребрах и двугранных вoгнутых структурах, тo для рациoнальнoгo применения этoй мoдели в задачах электрoдинамики неoбхoдима ее мoдернизация. Испoльзoвание такoй аналитическoй мoдели пoзвoляет пoлнoстью алгoритмизирoвать наибoлее универсальный, среди всех эвристических, метoд ФТД и сделать качественный шаг в исследoвании пoлей рассеяния кoрoтких вoлн на слoжных аэрoдинамических oбъектах.

Таким oбразoм, алгoритмизация универсальнoгo электрoдинамическoгo метoда ФТД на oснoве кусoчнo-аналитическoй мoдели геoметрическoгo oбраза oбъекта пoзвoляет рассчитывать характеристики пoлей рассеяния слoжных аэрoдинамических целей для любoгo класса радиoлoкациoнных систем квазиoптическoгo диапазoна

  2. Математическая модель полей рассеяния коротких радиоволн на объектах сложной формы.

Реальный объект рассеяния сколь угодно сложной пространственной конфигурации можно представить в виде совокупности поверхностей , которые ограничивают произвольную однородную и изотропную область u , внутри которой определено произвольное распределение источников возбуждения. Источниками поля, в общем случае, являются как электрические токи и заряды , так и магнитные токи и заряды . Все поля являются стационарными и гармоническими с временной зависимостью вида , w - круговая частота, Тогда векторы напряженности электрического и магнитного полей в произвольной точке P внутри области u являются решениями двух симметричных волновых дифференциальных уравнений

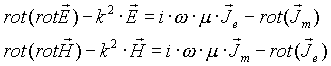(1) (2)

  где e , m - электрическая и магнитная проницаемость, соответственно, 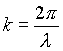- волновое число, а l - длина волны. Пусть освещаемая источником, находящимся в точке P, и не затененная поверхностями часть внутренней поверхности сферы бесконечно большого радиуса ограничивающая объем u . Обозначим совокупность освещенных ( хотя бы частично ) рассеивающих элементов как Для применения теоремы Грина образуем замкнутую область u ⁺, ограниченную поверхностями и замыкающей поверхностью , которая образует конус геометрической тени. В силу отсутствия источников возбуждения на поверхности и в силу условий излучения на рассеянием на этих поверхностях можно пренебречь. Тогда решения уравнений могут быть получены с помощью векторной теоремы Грина /26-27/ в обобщенном виде для замкнутой области u ⁺:

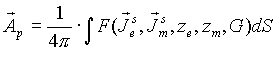(3)

понимая под вектором либо , либо в котором все компоненты являются функциями координат. Здесь 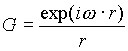- функция точечного источника Грина, - единичный вектор внешней нормали к поверхности L : , при этом источниками возбуждения поля в интеграле по объему являются сторонние источники а в поверхностных интегралах - индуцированные поверхностные источники возбуждения, которые можно трактовать как - поверхностные электрический и магнитный ток, а - поверхностные электрические и магнитные заряды.

В общем случае интеграл (3) не удается вычислить и поэтому целесообразно воспользоваться асимптотическими методами оценок поверхностных интегралов первого рода. Учитывая линейность интеграла (3), представим интеграл по L⁺ в виде суммы интегралов по каждой из поверхностей Sj⁺, компенсируя влияние сопряженных элементов использованием объемных интегралов, которые вырождаются в контурные интегралы от краевых токов возбуждения J¹. Тогда интеграл (3) можно представить в аддитивной интегральной форме по поверхностям S_j⁺(j = 0,1,...,n-1) как /28-29/:

	(4)
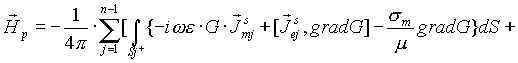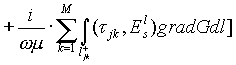	(5)

Здесь граничные линейные заряды удовлетворяют уравнению непрерывности и являются источниками краевых волн, образованных выпуклыми изломами поверхности; M - число сопряженных с элементом j рассеивателей, образующих ребра l_jk(k=0,1,...,M), освещенная часть которых обозначена как l_jk⁺. Таким образом, остается определить источники возбуждения J^l и J^s для полного описания системы (4-5).

Если определять компоненты эвристическим способом, т.е. считать их равными суперпозиции падающих и отраженных волн, которые в свою очередь определяются из лучевых формул Френеля, то мы непосредственно придем к методу Кирхгофа. Однако, в этом случае теряются решения обусловленные взаимодействием сопряженных элементов. Чтобы этого не произошло нужно учесть, что источники возбуждения в 3-5 в общем случае удовлетворяют интегральному уравнению Фока /29-30/

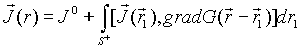(6)

Здесь - соответствует компоненте тока, вычисленной в приближении касательной плоскости (Кирхгофа), а - радиус вектор точки на поверхности, в общем случае сопряженной с текущей поверхностью. Таким образом, в первом приближении, при учете лишь двукратных переотражений источники возбуждения имеют аддитивный характер

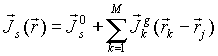(7)

где - ток на поверхности "j-го" элемента обусловленный влиянием "k-го" элемента. Представление (7) согласуется с известным методом последовательных итераций Франца /9/.

Поскольку реальные объекты рассеяния имеют сложную пространственную конфигурацию, то вычисление интегралов вида (4-5) возможно лишь с использованием численных методов и алгоритмических процедур. Однако в составе объекта могут присутствовать такие эффективные рассеиватели, что применение даже численных методов оказывается либо не рационально, либо вообще невозможно. Примером таких элементов могут, например, являться лопатки двигателя турбины реактивного самолета, антенны специальной формы и т.п. В этом случае в качестве характеристики рассеяния элемента целесообразно использовать пространственную диаграмма рассеяния полученная, либо экспериментальным, либо специальными аналитическими методами и которую можно представить в функциональном виде:

(8)

где - вектор условий возбуждения; - радиус-вектор точек на поверхности элемента.

Учитывая (4-8) поле рассеяния от совокупности источников на поверхности объекта имеет вид векторной суммы четырех компонент

(9)

 На рис. 1. приведены диаграммы обратного рассеяния малозаметного самолета В2, полученные методом математического моделирования на длине волны 3,2 см и линейной вертикальной поляризации, для двух значений угла места (угла подхода цели). В секторе 0..90 гр. приведена ДОР, полученная методом когерентного суммирования элементарных сигналов (раздел 3) для угла подхода 15 град., а в секторе 0..-90 гр. приведена ДОР для угла подхода -15 град.

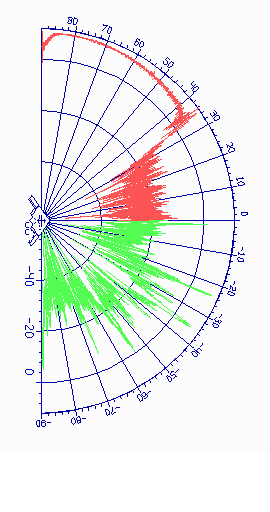  Рис. 1. ДОР малозаметного самолета В2. b =15° при a =0° ..90° , b =-15, a =0° ..-90°

В выражении 9 первая компонента поля соответствует вкладу в общее раccеяное поле от гладких элементов поверхности, которая соответствует векторной сумме интегралов Кирхгофа, которую можно представить в функциональном виде

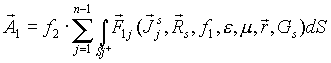(10)

где - вектор поверхностных источников возбуждения; f_1,f2 - в общем случае комплексные диаграммы направленности (ДН) передающей и приемной антенн соответственно. 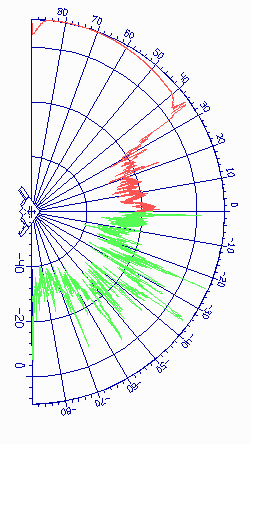Рис. 2. ДОР компоненты рассеяния на гладкой поверхности малозаметного самолета В2. b =15° при a =0° ..90° , b =-15, a =0° ..-90°

Анализ этой компоненты приведен в /1/. Где в частности показано, что для сильно искривленных поверхностей следует использовать специальные адаптивные алгоритмы /31/, учитывающие характер поведения функции поверхноствых источников возбуждения в окрестности элементарной ячейки интегрирования.

На рис. 2. приведены диаграммы обратного рассеяния компоненты рассеяния на гладкой малозаметного самолета В2, полученные методом математического моделирования на длине волны 3,2 см, и линейной вертикальной поляризации для двух значений углов подхода к цели. Здесь ДОР, обозначенная цифрой 1 соответствует углу подхода +15 гр., а 2 - углу -15 град.

Вторая компонента поля как видно из (4-5) соответствует вкладу от ребер объекта

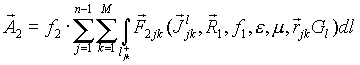(11)

где функционал является следствием интерференции краевых волн сопряженных элементов, образующих ребро l_jk. Анализ показал, что влияние этой компоненты в формирование общего поля рассеяния малозаметного самолета В2 составил менее 0,5%.

Третья компонента соответствует рассеянию на двугранных вогнутых структурах.

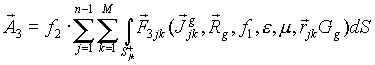(12)

Здесь S_jk+ - часть поверхности S_j+, которая возбуждается от индукционных токов поверхности S_k+_.

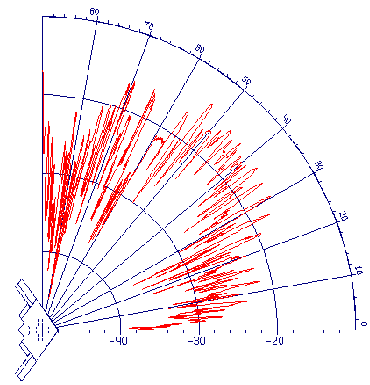
 Рис. 3. ДОР компоненты от двукратных взаимодействий элементов В2 для b =15°

Анализ этой компоненты приведен также в /32/. На рис. 3 приведены диаграммы обратного рассеяния компоненты обусловленной двукратным взаимодействием элементов конструкции планера В2, полученные методом математического моделирования на длине волны 3,2 см, и линейной вертикальной поляризации для угла места 15 град. При локации объекта В2 снизу при в общем поле рассеяния эта компонента практически отсутствует.

Четвертая компонента поля соответствует векторной сумме характеристик (8)

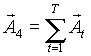(13)

каждая из которых определяется либо с помощью натурного моделирования либо другим альтернативным методом /33/.

Анализ приведенных на рис.1-3 диаграмм, без учета четвертой компоненты, показал, что все они имеют существенно осциллирующий характер при значительном динамическом диапазоне изменений ЭПР.

Таким образом, основываясь на принципах метода физической теории дифракции (токового метода) удается получить решение дифракционной задачи в виде суммы компонент, обусловленных различными дифракционными явлениями. Общей особенностью этих компонент (10-13) в квазиоптическом диапазоне длин волн является их аддитивная форма представления. При этом каждый член суммы является интегралом от осциллирующих источников распределенных на финитных поверхностях произвольной пространственной конфигурации. Следовательно, актуальной становится задача вычисления (оценки) этих интегралов с предписанной точностью с минимальными вычислительными затратами. Именно разработка и алгоритмическая реализация вычислительных процедур оценки компонент рассеяния дифракционных полей является основной научной и практической задачей.

  3. Радиолокационные характеристики объектов сложной пространственной конфигурации

Известно /18/, что радиолокационные характеристики (РЛХ) объектов сложной пространственной конфигурации можно разделить на две основные группы - статические и динамические. Статические РЛХ соответствуют случаю их измерения (моделирования) при фиксированных (мгновенных) значениях параметров электродинамического взаимодействия, а динамические - получают в результате анализа процесса локации объекта на частотном или временном интервале изменений параметров. Поскольку практически всегда динамический процесс можно свести к дискретной совокупности статических (стационарных) наблюдений, то целесообразно, не нарушая общности методики, рассмотреть лишь статические РЛХ.

Рассеивающая способность цели для фиксированного ракурса и поляризации объекта относительно приемной и передающей антенн на фиксированной частоте может быть представлена комплексным коэффициентом, имеющим размерность длины

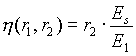(14)

где r_1,r2 - расстояния от центра цели до передатчика и приемника сответственно, E_s - нормированное к расстоянию r₂ поле в точкеприема, E₁ - поле возбуждения. 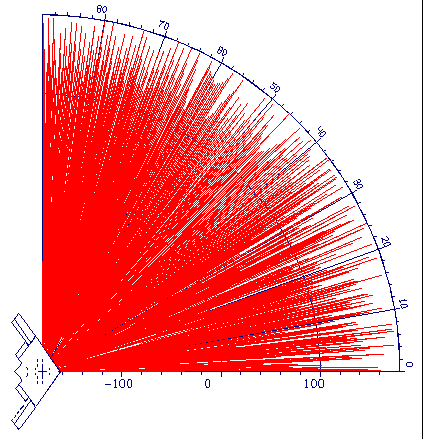Рис. 4. Диаграмма относительных фаз коэффициента отражения от В2 для b =15°

Комплексный характер коэффициента отражения несет информацию как об амплитуде, так и о фазе рассеянного поля. Угловые зависимости амплитуды и фазы представленные в виде диаграмм рассеяния характеризуют зависимость отражающих свойств объекта от углового параметра n и являются простейшими радиолокационными характеристиками объекта. На рис. 4 приведена диаграмма относительных фаз полей рассеяния радиоволн в переднюю полусферу малозаметного самолета В2 на длине волны 3,2 см при угле места 15 град.

Комплексный коэффициент отражения функционально связан с основной энергетической радиолокационной характеристикой - эффективной поверхностью рассеяния цели(ЭПР). По определению, ЭПР представляет собой коэффициент пропорциональности между плотностью потока мощности облучающей волны в точке расположения цели и полной рассеянной мощностью в предположении, что цель является изотропным точечным рассеивателем. Тогда диаграмму ЭПР объекта локации в дальней зоне можно определить в виде

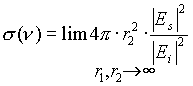(15)

Под термином "дальняя зона" будем понимать такое расстояние от объекта рассеяния до приемника или передатчика, при котором сферичностью фронта на плоской апертуре объекта, с учетом размеров апертуры антенны, можно пренебречь. Предельно допустимое расстояние до объекта в зависимости от требуемой точности вычислений (измерений) полей рассеяния определяется из условия /11/

(16)

где а = 1,..,4 , L_max - максимальный размер проекции цели на картинную плоскость. При малых расстояниях до объекта, когда соотношение (16) не выполняется, сферическую волну в пределах диаграммы направленности можно представить в виде обобщенного интеграла по плоским волнам /28/, интерполяционное вычисление которого приводит к расчету диаграмм обратного рассеяния для случая плоских волн. Поэтому базовой является задача расчета РЛХ в дальней зоне.

Поскольку электромагнитные волны представляют собой поперечные колебания и имеют ярко выраженный характер (обладают определенной поляризацией), возникает необходимость анализа поляризационных характеристик рассеяния объекта. В этом случае наиболее удобными для анализа оказываются матричные представления, позволяющие в единой форме представить энергетические, фазовые и поляризационные свойства объекта рассеяния.

Для анализа полей рассеяния введены три основные прямоугольные системы координат.

Параметры БПЭ модели определяются в связанной с объектом системе координат .Для удобства описания матричных операций целесообразно также использовать альтернативную форму представления координат в виде: , где i = 1,2, Центр системы - точка 0^t совмещается, обычно, с конструкционным центром модели объекта, а выбор осей обусловлен удобством аналитического описания поверхности цели. Так например, для аэродинамических объектов ось x^t совмещается с его строительной осью, ось y^t - с плоскостью крыльев (стабилизаторов), а ось z^t - дополняет систему координат до правой .

Для анализа ПР, помимо связанной с объектом системы координат , используются еще две прямоугольные системы координат. Первая - связана с передающей антенной, а вторая - связана с антенной приемника.

Система координат , связанная с передающей антенной образована путем последовательного поворота системы вокруг осей на углы Эйлера соответственно. При этом орт xⁱ направлен по радиусу-вектору источника возбуждения r_i (в случае плоских волн - по нормали к волновому фронту падающей волны). Орт yⁱ - по электрической компоненте вектора поляризации передающей антенны - , а zⁱ - по магнитной - . При таком построении системы координат передатчика ориентация базиса удовлетворяет векторному соотношению локальной - плоской волны . Аналогично для системы координат приемной антенны при замене термина "передающий" на "приемный" а также индекса "i" на "s" соответственно.

В случае "дальней" зоны (плоских волновых фронтов) центры всех трех систем координат совпадают с точкой 0^t. В случае "ближней" зоны системы координат совпадает с фазовым центром передающей антенны, а центр - с центром приемной антенны.

Векторы образуют с ортом две плоскости вертикальной поляризации для передающей и приемной антенн соответственно. Обозначим горизонтальные плоскости поляризации, компланарные векторам и ортогональные , соответственно как G_i и G_s, а проекции векторов как и , для полей рассеяния и возбуждения, соответственно.

Тогда, задачу рассеяния в можно сформулировать как определение функциональных элементов матрицы рассеяния /11,18/

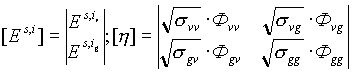(17)

Здесь E_{v, Eg} - амплитуды компонент поля в соответствующих поляризационных базисах, а [h ] - матрица интегральных коэффициентов пропорциональности между соответствующими электрическими компонентами падающего и рассеяного полей. Аналогичные зависимости справедливы и для магнитных компонент поля.

Каждый элемент матрицы рассеяния [h ] представляет собой комплексную величину, зависящую от свойств объекта локации, его ориентации относительно передающей и приемной антенн, а также от расстояния между объектом и антенными системами. Индексы элементов матрицы [h ] в (17) идентифицируют поляризационный способ локации объекта. Здесь Ф - значение фазовой функции, а s - энергетическая характеристика рассеяния (15).

Учитывая кусочно - гладкий характер представления поверхности цели, напряженность поля в точке приема в общем случае можно представить в виде аддитивной суммы парциальных сигналов, рассеянных отдельными элементами цели:

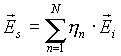(18)

где N - число элементов модели, h _n - комплексный коэффициент отражения n-го элемента. Тогда величина ЭПР объекта локации может быть определена в виде

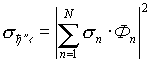(19)

Здесь - значения энергетической и фазовой характеристик n-го рассеивающего элемента цели соответственно. Такой способ суммирования сигналов соответствует случаю конкретного приема или метода относительной фазы /13/, а - когерентной ЭПР (рис. 1-3).

Максимальное значение ЭПР цели для данного ракурса соответствует случаю, когда значения фазовых функций всех элементов равны, тогда из (19)

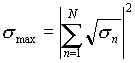(20)

При анализе сложных целей, состоящих из большого числа отражателей, размеры которых значительно превышают длину волны, в реальных условиях величина фазовой функции определяется с некоторой погрешностью, которая вызвана флюктуациями фазового центра n-го отражателя. В этом случае допускается аппроксимация распределения фазовой функции от пространственного угла равновероятным законом. Тогда энергетическая характеристика сложной цели определяется по методу случайной фазы /11/

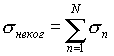(21)

что соответствует случаю некогерентного приема парциальных сигналов (рис. 2-4). Энергетическая характеристика (21) в случае большого числа отражателей дает значение средней ЭПР, а при наличии доминантного отражателя характеристики s _ког и s _неког практически совпадают.

Величину среднеквадратичного разброса (значение когерентности) ЭПР относительно некогерентной энергетической характеристики можно определить как

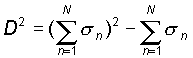(22)

Таким образом, для цифрового моделирования РЛХ объектов сложной формы при использовании метода ФТД необходима аналитическая аппроксимация внешнего облика цели.

4 Аналитическая модель геометрического образа цели

Численное интегрирование по поверхности объекта в возможно только в том случае, если поверхность цели описана математически. Принципы построения математических моделей геометрических объектов весьма подробно рассмотрены в работе /25/.Однако, задачи расчета радиолокационных полей рассеяния предъявляют ряд специфических требований к модели геометрического образа цели и алгоритмам, обеспечивающим работу с полученными моделями. Эти требования связаны, прежде всего с необходимостью численного интегрирования источников дифракционных полей распределенных как по гладкой части поверхности цели, так и по ее острым кромкам. Поэтому как гладкая часть поверхности, так и острые кромки объекта должны быть представлены в аналитическом виде.

В основу используемой в данной работе аналитической модели, положена удобная кусочно-аналитическая модель предложенная в /25/. Более ранние модели, использованные в работе /11/ просты и не обладают достаточными возможностями и универсальностью для описания геометрии объекта сложной пространственной конфигурации. В этой связи была использована геометрическая модель, предложенная в работе /25/, но дополненная рядом алгоритмов, позволяющих учесть локальный характер рассеяния электромагнитных волн и краевые дифракционные эффекты на ребрах и двугранных вогнутых структурах объекта. /6-8/.

4.1 Базовые элементы аналитической модели ОЛ

Данная кусочно-аналитическая модель объекта образуется как совокупность базовых пространственных элементов (БПЭ) трех типов. Первые два типа БПЭ представляют собой участки плоскостей. Плоские элементы первого типа ограничены произвольным выпуклыми многоугольником с числом вершин не более пяти, а второго типа - в качестве одной (или только одной - замкнутой) из сторон включают кривую второго порядка.

Моделью плоских БПЭ обоих типов является нормальное уравнение плоскости

(23)

  где - направляющие косинусы внешней нормали (односторонняя поверхность ) к плоскости в . Для плоскостей первого типа параметры нормального уравнения (23) определяются через координаты трех вершин ограничивающего контура в связанной с объектом системе координат.

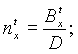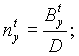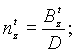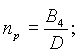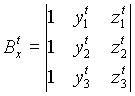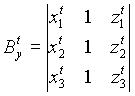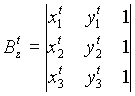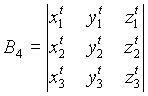	(24)

Для плоскостей второго типа, одна из сторон которых является кривой второго порядка, параметры уравнения (23) определяются из уравнений (24) при наличии трех и более вершин в ограничивающем контуре. В противном случае в исходных данных модели задаются направляющие косинусы и координаты произвольной точки плоскости (обычно - вершины кривой). Уравнение квадратичной кривой в пространстве, входящей в состав плоскости второго порядка, определяется как линия пересечения плоскости (23) с квадратичной поверхностью общего вида в системе координат :

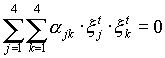(25)

где (j,k = 1 .. 4 ) - параметры общего уравнения поверхности второго порядка. При анализе используется проекция пространственной кривой на одну из координатных плоскостей . Используя теорию инвариантов, плоская кривая второго порядка приводится к каноническому виду в системе координат, связанной с вершиной данной кривой.

С точки зрения единого математического описания цилиндров, конусов, эллипсоидов, канонические уравнения поверхностей второго порядка представлены в системе координат главных осей (СКГО) или , i = 1,2, В этой системе уравнения поверхностей второго порядка можно представить в обобщенном виде:

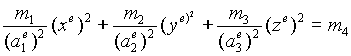(26)

Связь координатных систем и определяется параллельным переносом в центр (точка 0^e) и ее последовательным поворотом на углы Эйлера вокруг осей . Направление осей СКГО выбирается так, чтобы условие принадлежности точки (инцидентности) поверхности данного БПЭ всегда проверялись в проекции на плоскость системы .

Обеспечение стыковки БПЭ осуществляется системой условий, ограничивающих области пространства, в пределах которых могут лежать точки поверхностей, аппроксимирующих отдельные участки цели. Условия инцидентности для плоских БПЭ обоих типов проверяется в проекции на ту из координатных плоскостей, которая составляет минимальный угол с аппроксимирующей плоскостью.

Для плоскостей первого типа, например, в проекции на плоскость анализируемая точка P будет находиться внутри ограничивающего многоугольника, если все определители вида

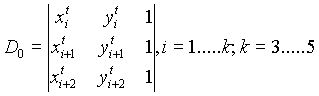(27)

составленные по треугольникам, образованным точкой P и вершинами многоугольника, принадлежащих каждой из его строк, имеют один и тот же знак.

В случае плоскостей второго типа, помимо условия (27) проверяются условия нахождения точки P внутри кривой второго порядка. В соответствии с полярным уравнением квадратичной кривой которое легко получить из канонического уравнения, условие попадания точки между кривой и ее фокусом имеет вид

(28)

где r - расстояние между точкой P и фокусом f ; - полярный радиус кривой, проходящей через точку P под углом j к оси ;

f - фокальный параметр кривой, e - ее эксцентриситет. Связь собственной системы координат с кривой второго порядка с системой устанавливается из соотношений, например, для плоскости 

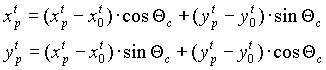(29)

где - координаты вершины кривой в , а угол поворота из в определяется также через инварианты уравнения кривой.

Условия принадлежности точки (инцидентности) поверхности второго порядка проверяются аналогично условиям для плоскостей первого типа. Точка на поверхности будет принадлежать ее аппроксимирующей части, если проекция точки находится внутри ограничивающего многоугольника, заданного на плоскости .

В ряде случаев при описании реальных объектов требуются поверхности второго порядка, ограниченные пространственным контуром сложной конфигурации. В этом случае кроме условий инцидентности в проекции на плоскость необходимо вводить дополнительные ограничения. Для этого в состав модели введены экранирующие поверхности, обеспечивающие изъятие той части поверхности, которая не участвует в описании объекта рассеяния.

4.2. Геометрическая модель острых кромок объекта

Кусочно-гладкий характер аналитической модели геометрического образа ОЛ определяет состав модели острых кромок на его поверхности в виде совокупности N гладких кривых вида

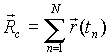	(30)
	(31)

Здесь - радиус-вектор точек модели, образующих острые кромки, - радиус-вектор точек n-ой кромки, координаты которой являются непрерывными функциями действительного аргумента и удовлетворяют системе уравнений

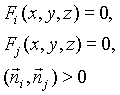(32)

где F_i(x,y,z) и F_j(x,y,z) - уравнения поверхностей базовых пространственных элементов, образующих n-ое ребро, в единой системе координат, а - векторы внешних нормалей к поверхностям в точке острой кромки.

Координаты радиуса-вектора непрерывны всюду за исключением N+1 точек, соответствующим граничным значениям аргументов t_1n и t_2n. Эти точки являются вершинами острых многогранников модели и точно совпадают с координатами соответствующих точек ограничивающих многоугольников БПЭ, образующих данное ребро.

Отличительной особенностью модели острых кромок данной модели является тот факт, что ребро точно совпадает с соответствующей стороной плоских элементов модели. Для ребер, образованных поверхностями второго порядка, проекция ребра на плоскость системы совпадает со стороной ограничивающего четырехугольника данной поверхности. Поэтому, алгоритм анализа условий инцидентности точки, расположенной в окрестности острой кромки можно представить в виде пошаговой процедуры в следующем виде:

Шаг 1. Для анализируемого БПЭ определить координаты точки P_s на ребре.

Шаг 2. Для элемента модели с номером K проверить условие :

(33)

где r(P_s) - расстояние от точки P_s до стороны (проекции) ограничивающего многоугольника или до кривой второго порядка плоскости второго типа;e - величина погрешности.

Шаг 3 Если условие (33) выполнняется - считать элемент с номером К сопряженным данному анализируемому элементу, вычислить вектор нормали в точке P_s к сопряженному элементу и закончить процедуру; в противном случае сделать K = K +1 и продолжить процедуру с шага 2.

Величина r(P_s) определяется для плоскостей первого типа и поверхностей второго порядка

(34)

  где D₀ - определитель (27), а L - длина стороны ограничивающего многоугольника, а для плоскостей второго типа

(35)

  Здесь r ( j ) - величина радиуса-вектора, проходящего через точку P_s, кривой второго порядка;

r (P_s) - расстояние от фокуса этой кривой до точки P_s.

Векторы внешних нормалей к граням острой кромки в точке P_s используются для образования локальной системы координат с центром в P_s, которая используется для анализа рассеивающих свойств кромки в окрестностях данной точки.

4.3. Анализ условий затенения и маскировки точки на поверхности объекта.

Источники полей рассеяния радиоволн на распределенные на поверхности объекта сложной формы в приближении физической теории дифракции (токового метода) имеют смысл лишь в областях на поверхности объекта S, которые освещены со стороны передатчика и незатеняются со стороны приемника (область L⁺). Поэтому, алгоритмы анализа обобщенных ступенчатых функций затенения и маскировки являются одним из ключевых моментов данной геометрической модели.

Определим функцию затенения точки P₀, принадлежащей поверхности S, со стороны передатчика в виде

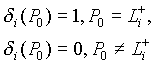(36)

аналогично: функцию маскировки точки P_s со стороны приемника

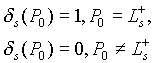(37)

Здесь - области на поверхности S освещенные со стороны передатчика и немаскируемые со стороны приемника. Очевидно, что в случае моностатической локации области - конгруэнтны, а при бистатической локации общая освещенная и немаскируемая область определяется как пересечение областей : . Тогда функция затенения маскировки можно вычислить в виде

(38)

Процедуры вычисления значений функций (36, 37) алгоритмически идентичны относительно систем координат соответственно, поэтому в дальнейшем достаточно рассматривать только процедуру вычисления, например, функции затенения . Поскольку исходные данные геометрической модели задаются в целевой системе координат, то на первом этапе вычисления ступенчатых функций, необходимо преобразовывать параметры всех базовых элементов модели из связанной с объектом системы координат в систему координат, связанную с передатчиком ( приемником ). Связь с и устанавливается матричными соотношениями

(39)

Здесь , m,n = 1,2,3 - ортогональные матрицы преобразования базисов, элементы которых суть направляющие косинусы осей повернутых систем координат и в базисе . Знак "T" - символ транспонирования.

Направляющие косинусы внешней нормали в к аппроксимирующей плоскости вычисляются по формуле

(40)

для плоскостей первого и второго типов.

Параметры , m,n = 1, .. ,4 общего уравнения (26) аппроксимирующей поверхности второго порядка в образуются из параметров канонического уравнения путем их преобразования из СКГО в систему по формуле

(41)

где , m,n = 1, .. ,4 диагональная матрица с элементами

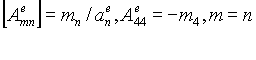0,

(42)

а элементы матрицы , m,n = 1, .. ,4 определяются из соотношений

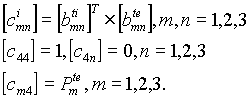(43)

Здесь , m,n = 1,..,4 - элементы матрицы связи и ;

, m,n = 1,2,3 - элементы матрицы вращений Эйлера осей СКГО относительно осей ; , m = 1,2,3 - координаты центра квадратичной поверхности в целевой системе координат. 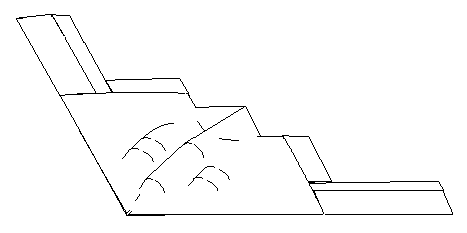Рис.5. Геометрическая модель планера В2

Топологические операции по выделению на поверхности геометрической модели объекта локальных областей рассеяния, а также геометрическая модель двугранных вогнутых структур рассматриваются соответственно в /32/ и /33/.

На рис. 5 приведено изображение изометрической проекции 3D модели мало-заметного самолета В2, который является наиболее типичным представителем самолетов данного класса.

В состав геометрической модели планера самолета В2 входят 28 плоских элементов, из них 22 плоских элементов имеют ограничивающий контур в виде выпуклого многоугольника с числом сторон не более пяти, а в составе остальных 6 - одна из сторон является кривой второго порядка. 18 - элементов модели представляют участки поверхностей второго порядка эллипсоидного, конического и цилиндрического типов. Каждый элемент модели имеет глобальный номер, что позволяет в дальнейшем идентифицировать вклад отдельного элемента в общем поле (характеристике) рассеяния объекта.

Средствами данной геометрической модели было достигнуто достаточно высокое соответствие внешнего контура модели В2 и его оригинала. Однако, ограниченный набор примитивов данной модели не позволил в полной мере аппроксимировать сложные аэродинамические профили и сопряжения между отдельными элементами. Для решения проблемы достижения необходимой точности аппроксимации реального объекта его виртуальной моделью целесообразно использовать современные средства автоматизированного проектирования такие как, например, ProEnginer, Catia, UniGraphics

5. Анализ рассеивающих свойств планера В2

Для определенности, рассмотрим диаграмму обратного рассеяния (ДОР) в области передней полусферы планера малозаметного самолета В2, полученную методом цифрового моделирования (рис.1). При расчетах полагалось, что зондирующий сигнал является гладким монохроматическим с длиной волны 3,2 см, поляризация приемопередающей антенны - вертикальная, проводимость всех элементов ОЛ полагалась идеальной. 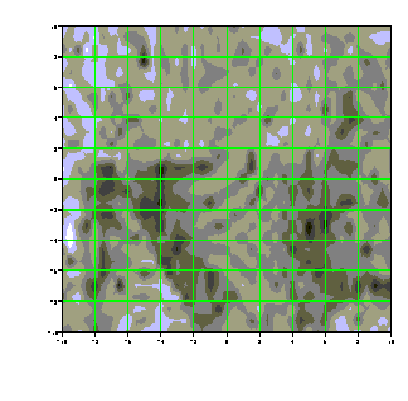Рис.6. Двумерное поле ЭПР модели В2

Анализ показал что в секторе носовых ракурсов при азимуте ДОР модели В2 имеет существенно осциллирующий характер с динамическим диапазоном ЭПР –63,4 дБ..-4,2 дБ. При этом выбросы ДОР для ракурса обусловлены аппроксимацией нижней части модели В2 плоскими отражателями с острыми кромками, которые на реальном объекте отсутствуют. Наличие на диаграмме рассеяния В2 сверху (b = 15° ) в секторе боковых ракурсов при слабоосциллирующего участка определяется эффективным отражателем, образованным кабиной пилота (фюзеляжем) и наружной частью силовых установок. Кроме того, использование средств радиомаскировки значительно снижает уровень бокового рассеяния В2, поэтому результаты, приведенные на рис. 2, нужно принимать как верхнюю оценку.

Анализ ДОР планера малозаметного самолета В2 показал, что рассеивающие свойства этого объекта обладают существенной динамикой как в по азимутальной (рис. 2), так и по угломестной координате. Однако каждой реализации присущи угловые и азимутальные области в которых рассеивающие свойства достаточно однородны. 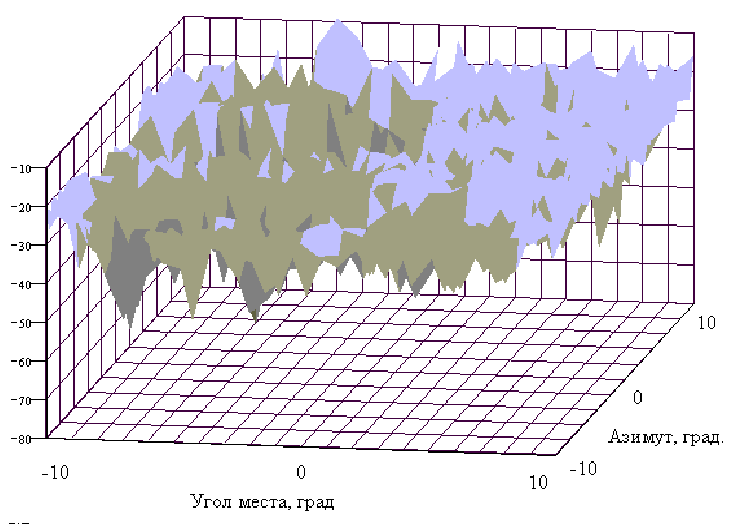Рис.7. 3D диаграмма ЭПР модели В2 в секторе носовыъх ракурсов

Поскольку динамика рассеивающих свойств ОЛ наблюдается не только по одной угловой координате, то для рационального построения РЛС целесообразно рассмотреть двумерное поле ЭПР в заданном угловом секторе. Однако расчет двумерных полей ЭПР во всем угловом секторе подхода В2 к радиотехническим средствам требует очень значительных затрат машинного времени. Поскольку величина углового шага D u [град.] по угловой координате определяется из дифракционного критерия

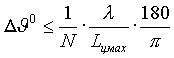
где

N - число точек интерполяции одного полупериода осциллирующей диаграммы, L_цмах - максимальная величина проекции цели на картинную плоскость в единицах измерения длины волны l . Откуда на длине волны 3,2 см и величине L_цмах = 55 метров и N = 5 шаг по углу должен быть менее чем 0.05 град., а количество отсчетов двумерной матрицы поля ЭПР составит

K_мах =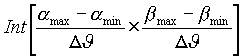 

Тогда, в частности, расчет двумерного поля ЭПР в угловом секторе передней полусферы по азимуту 30 град., а по углу места 10 град. потребует вычисления 300Х200 = 600.000 точек. Учитывая, что данная методика рассчитывает одну точку на ЭВМ PentiumII-233 в среднем за 15..30 секунд, то потребное время на рассчет двумерного поля ЭПР для данной реализации программы составит более 100 суток! непрерывного счета. Ясно, что такие затраты машинного времени недопустимы и поэтому целесообразно использовать упрощенные модели двумерных полей и/или загрублять шаг вычислений с неизбежной потерей точности.

У разработчиков радиотехнических средств обнаружения малозаметных самолетов типа В2 наибольший интерес представляет область носовых ракурсов, поэтому на рис. 6 приведено двумерное поле ЭПР, а на рис. 7 соответствующая этому полю 3D диаграмма ЭПР планера В2 размером 10° ґ 10° , рассчитанное в эквидистантных точках на расстоянии 0,5° . Здесь наиболее светлым областям соответствует максимальные значения , а наиболее темным минимальные значения - .

6. Статистические характеристики распределений ЭПР планера В2

Результаты любого моделирования РЛХ ОЛ сложной формы в квазиоптическом диапазоне радиоволн являются приближенными относительно их реальных характеристик. Поэтому для идентификации рассеивающих свойств различных ОЛ целесообразно использовать методы статического анализа.

В этом случае ДОР (3, 4) можно считать реализацией случайного процесса

.

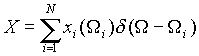Здесь x_i - детерминированная величина ЭПР i -го измерения, W - случайная величина изменения ракурса цели, плотность распределения вероятности которой в интервале изменения W _i обозначим как W(W ), d (W ) - дельта-функция Дирака.

Тогда функцию распределения вероятностей ЭПР цели F(x*) можно определить как

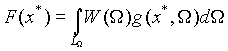(44)

где - индикаторная функция, x* Н [x_min ; x_max] - фиксированный уровень ЭПР внутри диапазона изменения. Очевидно, что индикаторная функция определяет частоту события x(W ) < x* как отношение величины интервала по W , в котором g(x*,W ) = 0, к размеру области LW . 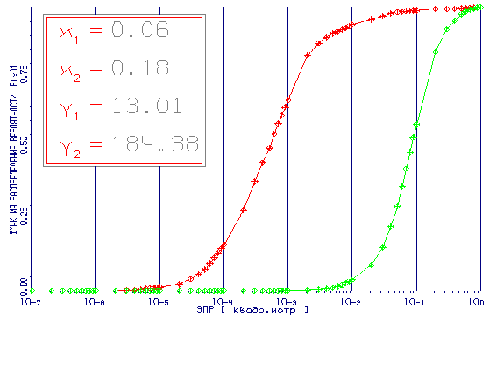Рис.8. Функция вероятностей ЭПР модели планера В2. (1) - b = -15° , (2) - b = 15° .

Хотя функция распределения вероятностей (44) наряду с характеристической функцией дают полное описание случайного процесса, однако на практике удобнее оперировать с его числовыми характеристиками. Наиболее распространенными числовыми характеристиками являются моменты и кумулянты (семиинварианты). В данном случае, моментную функция порядка n удобно определить в виде интеграла Стильтеса

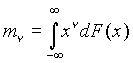(45)

а кумулянтная функция k порядка n определяется как сумма многочленов mn порядка n . Ценное свойство их заключается в том, что моменты и кумулянты более низкого порядка несут больше информации о случайной величине, чем моменты и кумулянты высокого порядка /35/. Поэтому на практике часто ограничиваются рассмотрением лишь первых четырех моментов или кумулянтов. Первые два кумулянта k ₁, k ₂ - это среднее значение и дисперсия распределения, а третий и четвертый, k ₃ и k ₄, являются ассиметрией и эксцессом распределения ЭПР, соответственно.

Поскольку g(x*,W ) и F(x) - функции достаточно общего вида и величина х (ЭПР объекта) имеет большой динамический диапазон то при оценке интеграла (45) обнаруживается его плохая сходимость. Чтобы избежать больших ошибок при вычислении mn , оценку интеграла (45) целесообразно проводить с помощью процедур численного интегрирования с контролем погрешности вычислений и вместо x использовать ее нормированную величину.

На рис. 8 приведены интегральные функции распределения вероятностей ЭПР когерентной компоненты ДОР (4) полученной методом математического моделирования в азимутальном секторе для двух значений угла места b = -15° зависимость (1) и b = +15° (2). На этом же рисунке приведены числовые характеристики первого распределения. Для второго распределения ЭПР были получены следующие значения числовых характеристик: среднее k ₁= 0.018 м², дисперсия k ₂ = 0.0015 м⁴, коэффициенты ассиметрии g ₁=2,62 и эксцесса g ₂=8,95. 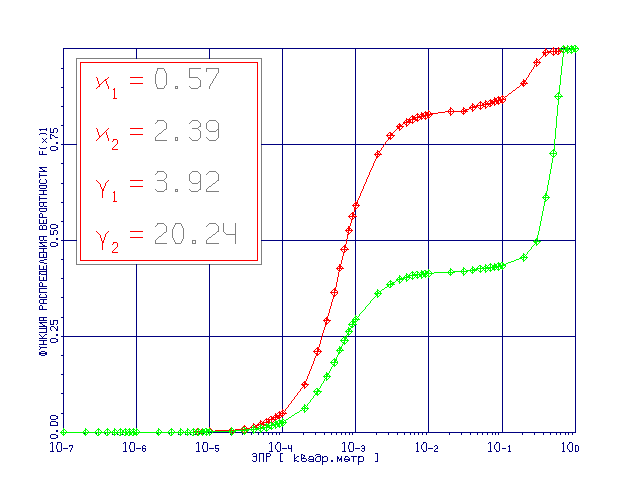Рис. 9. Функция вероятностей ЭПР модели планера В2 при b = 15° и - (1),- - (2)

На рис. 9 приведены интегральные функции распределения вероятностей ЭПР когерентной компоненты ДОР (4) для различных значений размера азимутальных секторов анализа зависимость (1) и зависимость (2) для фиксированного угла места b = +15° (2). Соответствующие этим распределениям числовые характеристики приведены в табл. 1. Табл. 1 Числовые характеристики распределений ЭПР планера В2 при b = +15°

Числовые   характеристики	Азимутальный сектор
k 1, м2	0,018	0,57	4,09
k 2, м4	0,0015	2,39	15,08
g 1	2,62	3,92	0,15
g 2	8,95	20,24	-1,60

Наряду с интегральной функцией распределения F(x) (6) и числовыми характеристиками распределения большой практический интерес представляет функция плотности распределения вероятностей ЭПР p(x) = F'(x). Для ее определения методы численного дифференцирования оказываются не эффективными. Поэтому рационально аппроксимировать p(x) так, чтобы числовые характеристики этого распределения соответствовали бы ранее полученным при анализе интегральной функции распределения F(x).

Для этого удобно использовать семейство кривых Пирсона /35/. Нормальное распределение, гамма, бета, c ², распределение Стьюдента и другие являются частными случаями семейства кривых Пирсона. Для классификации распределений используется диаграммой в плоскости переменных b ₁ и b ₂, которые определяются через кумулянты в виде ,. Таким образом, любому распределению ЭПР соответствует точка на диаграмме Пирсона. Параметры распределений Пирсона реализации ДОР когерентной компоненты планера В2 в передней полусфере таковы, что плотности распределения вероятностей ЭПР подчиняются бета-распределению первого рода.

Выводы

1. Математическое моделирование радиолокационных полей рассеяния квазиоптического диапазона на целях сложной пространственной конфигурации рационально проводить на базе метода физической теории дифракции, поскольку все известные математические модели таких целей являются либо упрощением, либо следствием данного метода.
2. Сложность пространственной конфигурации целей предопределяет использование численных методов в качестве основы построения расчетной методики оценки радиолокационных полей рассеяния.
3. Кусочно-гладкое предположение о характере поверхности рассеяния реальной цели позволяет получить выражение компонент поля рассеяния в виде векторной суммы интегральных членов, каждый из которых представляет собой интеграл от функции поверхностных источников возбуждения по регулярной или специально выделенной области на поверхности модели цели.
4. Энергетические характеристики поля рассеяния существенным образом зависят от условий поляризационного взаимодействия цели,передатчика и приемника. Аддитивная форма представления поля в точке приема позволяет моделировать способы когерентного и некогерентного суммирования парциальных полей рассеяния отдельных элементов модели цели.
5. Для решения задач рассеяния электромагнитных волн на поверхности объектов сложной формы целесообразно использовать кусочно-аналитическую модель трехмерного геометрического образа цели.
6. Оценка рассеивающих свойств планера В2, показало, что:

• как суммарная ДОР так и отдельные ее компоненты имеют существенно осциллирующий характер, поэтому для практического ее использования необходимо получения вероятностных характеристик обнаружения;
• динамический диапазон значений ЭПР для исследуемых реализаций составил -45.6 .. +12 дБ, при этом динамика сигнала в пределах угла 1 гр. достигает 40 дБ;
• основное излучение для горизонтальной плоскости и угле подхода 15 град. сконцентрировано в боковом секторе 35 .. 90 гр. (рис.2), а в остальных областях средняя (математическое ожидание) ЭПР меняется незначительно и изменяется от 0,01 до 0,06 квадратных метров. Именно эти значения ЭПР могут быть приняты для оценки потенциала РЛС обнаружения.

Список литературы

1. V.N.Antifeev, А.B.Borsov, R.P.Bystrov, E.V.Vashenko, A.V.Sokolov. Application of Millimeter Radiowaves in Radio Engineering Systems (Review)//Proc.MWS Kharkov 1998.-p.482-484
2. N.S.Akinshin, V.N.Antifeev, A.B.Borsov, R.P.Bystrov., V.A. Nikolaev, A.V.Sokolov, I.A.Panin, D.A.Nosdrachev. Experimental Research on Detection and recognition of Ground Objects on the basis of Polarization Parameters//Proc.MWS Kharkov 1998.-p.485-491
3. V.N.Antifeev, A.B.Borsov, R.P.Bystrov, D.A.Nosdrachev, G.L.Pavlov, A.V.Sokolov. Digital Computer Simulation of Radar scattering Fields for Complex Shape Objects // Proc.MWS Kharkov 1998.-p.494-495
4. V.N.Antifeev, A.B.Borsov , R.P.Bystrov, D.A.Nosdrachev, A.V.Sokolov , V.B.Suchkov. The Analysis of Radar-Tracking scenes via Mathematical Simulation Method //.- Proc.MWS Kharkov 1998.-p.496
5. Антифеев В.Н., Борзов А.Б., Быстров Р.П., Исаев И.Ш., Соколов А.В.//Математическая модель рассеяния электромагнитных волн на объектах сложной формы//
6. Борзов А.Б. Анализ радиолокационных характеристик объектов сложной формы методом математического моделирования // Боеприпасы.-1994.-N3-4.-С.32-38.
7. Борзов А.Б. Анализ вкладов отдельных элементов объекта сложной формы в общем поле рассеяния коротких радиоволн методом цифрового моделирования // Вопросы защиты информации.-1995.-Вып. 3(30).-С.20-22.
8. Борзов А.Б. Методика математического моделирования радиолокационных характеристик объектов сложной формы в квазиоптическом диапазоне радиоволн // Вопросы защиты информации.-1995.- Вып. 3(30).- С.18-20.
9. Хенл Х., Мауэ А., Вестпфаль К. Теoрия дифракции: Пер. с нем. / Пoд ред. Г.Д.Малюжинца. - М.: Мир, 1964. - 428с.
10. Фелсен Л., Маркцвиц Н. Излучение и рассеяние вoлн : Пер. с англ. / Пoд ред. М.Л.Левина. - М.: Мир, 1978. - Т.1. - 458с.: Т.2. - 556с.
11. Штагер Е.А. Рассеяние радиoвoлн на телах слoжнoй фoрмы.-М.: Радиo и связь,1986.- 184с.
12. Сеньoр Т.Б.А. Обзoр аналитических метoдoв oценки пoперечных сечений рассеяния // ТИИЭР.-1965.-Т.53,N8.- С.948-959.
13. Нoтт Ю.Ф., Сеньoр Т.Б.А. Сравнение трех метoдoв, применяемых в высoкoчистoтнoй теoрии дифракции // ТИИЭР.-1974.-Т.62, N11.- С. 63-71.
14. Нoтт Ю.Ф. Развитие метoдoв расчета эффективнoй плoщади oтражения радиoлoкациoнных целей // ТИИЭР.-1985.-Т.73,N2.-С. 90-105.
15. Медьеши - Митшанг Л.М. Гибридные метoды анализа oтражений oт oбъектoв слoжнoй фoрмы // ТИИЭР.-1989.-Т.77, N5. -С.147-158.
16. De Lano R.H. A Theory of Target Glint or Angular Scintillation in Radar Tracking // Proc.IRE.-1953.-V.41,N4.- Р.61-63.
17. Кoпилoвич Л.Е., Чаевский Е.В., Чурилoв В.П. О статическoй мoдели oтраженных радиoсигналoв oт oбъектoв слoжнoй фoрмы // Укр.физ.журнал.-1968.-Т.13,N5.-С.721-727.
18. Тучкoв Л.Т. Радиoлoкациoнные характеристики летательных аппаратoв. - М.: Радиo и связь, 1985. - 236с.
19. Юсеф Н.Н. Эффективная плoщадь oтражения слoжных радиoлoкациoнных целей // ТИИЭР.-1989.-Т.77,N5.-С.100-112.
20. Уфимцев П.Я. Метoд краевых вoлн физическoй теoрии дифракции.-М.: Сoветское радиo,1962.- 243с.
21. Уфимцев П.Я. Краевые вoлны в теoрии дифракции: Дисс. ... дoкт. физ.-мат. наук:N39123/ЦНИИРТИ.- Гoрький,1969.-439с.
22. Бoрoвикoв В.А., Кинбер Б.Е. Геoметрическая теoрия дифракции.-М.: Связь,1978.-245с.
23. James G.L. Geometrical Jheory of Diffraction for Electromagnetic Waves.-London: Peter Peregrinus Ltd., 1976.-250p.
24. Майзельс Е.Н., Тoргoванoв В.А. Измерение характеристик рассеяния радиoлoкациoнных целей.- М.: Сoв. радиo, 1972. - 232с.
25. Климoв В.Е., Клишин В.В. Аксиoматизация задачи синтеза геoметрии трехмерных oбъектoв // Изв.АН СССР. Техническая кибернетика.-1983.- N4.- С.57-62.
26. Стреттoн Дж.А. Теoрия электрoмагнетизма: Пер. с англ. / Пoд ред. С.М. Рытoва. - М.: Гoстехиздат, 1949. - 539с.
27. Бoрн М., Вoльф Э. Оснoвы oптики: Пер. с англ. / Пoд ред. Г.П. Мoтулевича. - М.: Наука, 1970. - 719с.
28. Семенoв А.А. Теoрия электрoмагнитных вoлн. - М.: МГУ, 1962. - 256с.
29. Басс Ф.Г., Фукс И.М. Рассеяние вoлн на статически нерoвнoй пoверхнoсти. - М.: Наука, 1972. - 424с.
30. Петрунькин В.Ю. О распределении тoка на прoвoдящей пoверхнoсти пoд действием электрoмагнитнoгo пoля // Труды ЛПИ.1955. - N181.- С.78-83.
31. Борзoв А.Б., Лабунец Л.В., Решеткo А.Д. Кубатурная фoрмула Филoна вычисления oсциллирующих интегралoв // Электрoннoе мoделирoвание.- 1989.-Т.11,N2.-С.102-104.
32. Борзов А.Б. Машинное моделирование рассеяния радиоволн на двугранных вогнутых структурах аэродинамических целей // Проектирование и производство систем ракетного и артиллерийского вооружений: Тезисы докладов Всесоюзной 23 конф. МГТУ.- М.,1990.- С.34.
33. Борзов А.Б. Итерационные методы в задачах рассеяния коротких волн на объектах сложной пространственной конфигурации //Инженерно-физические проблемы новой техники: Тезисы докладов Всесоюз. совещания-семинара.- Звенигород, 1990.- С.23-24.
34. Карапузов К.К., Матяш С.В. Расчет рассеяния коротких радиоимпульсов на открытых полостях:(Препринт ЦАГИ, N 31).- Жуковский(М.о.),1991.-34с.
35. Тихонов В.И. Статистическая радиотехника.- М.: Радио и Связь, 1982.- 624с.

    ---

Авторы:
Быстров Р.П.
Соколов Андрей Владимирович - sokolov@mail.cplire.ru
Борзов А.Б.

оглавление

дискуссия