"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 12, 1999

оглавление

дискуссия>

А.Б.Борзов*, Э.А.Засовин**, А.В.Соколов***, В.Б. Сучков*
* - Московский Государственный технический университет им. Н.Э. Баумана,
** - Московский Институт радиотехники, электроники и автоматики
***- Институт радиотехники и электроники РАН

Получена 24 декабря 1998 г.

Для рационального построения бортовых РЛС необходимы анализ и синтез радиолокационных полей рассеяния от объектов сложной пространственной формы с учетом фона подстилающей поверхности. Совокупность участков естественного и антропогенного вида образуют радиолокационную сцену, элементы которой обладают электродинамическими и статистическими свойствами.

В соответствии с концепцией объектно-ориентированного программирования [2] процесс цифрового моделирования характеристик рассеяния ЭО осуществляется по следующим этапам:

1-й этап – инициализация базисов падающей и отраженной волн в системе координат ЭО [1] в соответствии с углами подхода , а также электродинамики каждого слоя покрытия пластины на основе параметров .

2-й этап – выбор метода расчета характеристик рассеяния ЭО в зависимости от наличия или отсутствия на поверхности пластины радиопоглощающего покрытия или хаотических неровностей .

4-й этап – определение ПМР ЭО на основе выбранного метода расчета.

В соответствии с приведенным процессом моделирования на 1-м этапе создаются 2 базовых класса, в одном из которых осуществляется инициализация базисов падающей и отраженной волн, а в другом - .электродинамика покрытия пластины и ее основного материала с учетом длины волны k-й спектральной составляющей зондирующего сигнала. Приватными данными 1-го класса являются соответствующие углы подхода падающей и отраженной волн , а защищенными данными, доступными другим классам - соответствующие вектора базисов и . В другом базовом классе приватными данными являются электродинамические параметры каждого слоя покрытия пластины (включая ее основной материал) и длина волны , а защищенными данными - комплексные электродинамические параметры слоев в зависимости от длины волны , , а также толщины каждого слоя. Защищенные данные 2-х базовых классов являются общими для всех методов расчета ПР ЭО, вне зависимости от характера его геометрической модели.

Наследниками рассмотренных базовых классов являются классы-методы, приватными данными которых являются параметры ЭО в зависимости от его геометрической модели, а общими данными - его характеристики рассеяния. Одним из наследуемых классов является класс, содержащий характеристики рассеяния идеально гладкой треугольной пластины. Приватными данными этого класса являются координаты вершин треугольной пластины в системе координат ЭО [1]. Кроме того, при наличии на поверхности пластины хаотических неровностей в соответствии с рассмотренными математическими моделями рассеяния радиоволн на такого типа ЭО, создаются 2 других класса-метода, содержащие характеристики рассеяния крупно- и мелкомасштабных неровностей на поверхности пластины. Приватными данными 1-го класса-метода являются статистические параметры крупномасштабной поверхности ЭО: , а приватными данными другого - параметры мелкомасштабных неровностей: . При этом механизм наследования может быть реализован и между классами-методами. Так, при наличии на поверхности пластины двух типов случайных неровностей создается еще один класс-метод, где в качестве общих данных используются характеристики рассеяния двухкомпонентной поверхности, а в качестве приватных данных применяется параметр Рэлея , являющийся критерием применимости методов определения характеристик рассеяния 2-х компонент неровностей поверхности пластины. Данный класс-метод является наследником от 2-х рассмотренных классов методов, содержащих параметры и функции рассеяния крупно- и мелкомасштабных компонент поверхности. Рассмотренный механизм наследования классов приведен на рис. 1.

На этапе выполнения программы первым шагом к определению характеристик рассеяния ЭО при выбранном методе расчета является создание объекта выбранного класса-метода. Под объектом класса-метода понимается ситуация облучения ЭО с заданными электродинамическими свойствами его покрытия и геометрическими параметрами в собственной системе координат ЭО [1]. При этом параметрами объекта класса-метода являются углы подхода падающей и отраженной волн, параметры электродинамики ЭО поверхности и длина волны , а также параметры характеризующие геометрическую модель ЭО. За счет механизма наследования при создании объекта класса-метода углы подхода передаются в базовый класс инициализации базисов, а параметры электродинамики - в класс инициализации комплексных электромагнитных параметров покрытия соответственно. Остальные параметры инициализируют выбранный класс-метод. Далее созданный объект класса-метода вызывает функцию рассеяния ЭО в соответствии с выбранным методом расчета. Таким способом осуществляется инициализация ПМР дискретного элемента сложного объекта. Тогда представляется возможным получение интегральных арактеристик рассеяния заданного объекта сложной формы.

С использованием рассмотренного объектно-ориентированного подхода к цифровому моделированию характеристик рассеяния дискретных элементов сложных сцен были получены индикатрисы рассеяния (рис. 2, 3) треугольной пластины при наличии на ней многослойного радиопоглощающего покрытия и случайных неровностей. При этом по оси ординат откладывалась ЭПР пластины приходящаяся на единицу ее площади , а по оси ординат угол места приемника в системе координат ЭО.

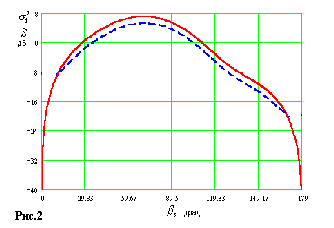
На рис. 2 приведены бистатические индикатрисы рассеяния гладкой идеально проводящей пластины с покрытием и без него на длине волны при согласованной вертикальной поляризации. При этом в качестве геометрической модели пластины принимался равнобедренный прямоугольный треугольник со стороной равной длине волны. В качестве покрытия пластины применялась 4-х слойная модель где первым слоем являлось антистатическое покрытие с , третьим слоем противоэрозийное покрытие с , а вторым и четвертым слоями - воздушная среда с . Толщины 1-го и 3-го слоев принимались равными 15 мм, а 2-го и 4-го слоев 20 мм соответственно.

Угол визирования падающей волны в системе координат ЭО . Из рис. 2 видно, что при наличии радиопоглощающего покрытия (штриховая линия) на поверхности пластины ее удельная ЭПР снижается на 3 дБ по сравнению с идеально проводящей пластиной (сплошная линия).

На рис. 3 приведены моностатические индикатрисы рассеяния для треугольной пластины со случайными неровностями, для которых были приняты статистические и электродинамические параметры поверхности асфальта : , , , , , . В качестве значений длины волны принимались , , . При этом графики были построены для согласованной вертикальной поляризации.

1. Рассмотренный объектно-ориентированный подход к моделированию процесса рассеяния радиоволн на ЭО сложной сцены позволяет определенным образом оптимизировать и структурировать процесс вычисления как элементов ПМР ЭО, так и интегральных характеристик рассеяния сложных объектов.

[1]. А. Б. Борзов. Анализ методов математического моделирования дифракционных полей рассеяния сложных сцен. (в печати).

[2]. Паппас К., Мюррей У. Си/Си++. Руководство программиста. Кн.2. М.:СК Пресс, 1997.

оглавление

дискуссия