ВЛИЯНИЕ ИМПЕДАНСНОЙ ПОВЕРХНОСТИ
ЦИЛИНДРА
НА ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ
Габриэльян Д.Д., Звездина
М.Ю., Костенко П.И.,
Ростовский военный институт ракетных войск
Получена 17 февраля 2000 г.
Анализируются закономерности
влияния импедансной поверхности кругового
цилиндра на характеристики излучения
крестообразного электрического вибратора.
Приводятся соотношения и результаты
исследований диаграммы направленности и
коэффициента эллиптичности
крестообразного излучателя при различных
значениях поверхностного импеданса и
радиуса кругового цилиндра.
Крестообразные электрические
вибраторы находят самое широкое применение
в антенной технике и как одиночные
излучатели, и как излучающие элементы
антенных решеток. Часто такие излучатели
располагаются вблизи цилиндрических
несущих конструкций, которые обладают
импедансными свойствами. Наличие указанных
конструкций приводит к эффектам
деполяризации электромагнитных волн
[1-5],
что может существенным образом исказить
характеристики направленности
крестообразного вибратора. Несмотря на
достаточно большое число работ,
посвященных исследованию влияния
цилиндрических идеально проводящих
поверхностей на характеристики излучения
различным образом ориентированных
вибраторов, например, [6,
7], аналогичные
аспекты для импедансных поверхностей не
нашли своего должного рассмотрения.
Целью данной статьи является
исследование влияния импедансной
поверхности бесконечного кругового
цилиндра на диаграмму направленности (ДН) и
поляризационные характеристики
крестообразного электрического вибратора.
Рассмотрим крестообразный
излучатель, образованный продольным и
поперечным дуговым электрическими
вибраторами, расположенными на удалении
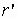 от оси импедансного кругового цилиндра
радиуса
от оси импедансного кругового цилиндра
радиуса 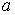 .
Длина плеча каждого из вибраторов равна
.
Длина плеча каждого из вибраторов равна 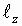 и
и 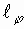 соответственно. Геометрия задачи приведена
на рис.1.
соответственно. Геометрия задачи приведена
на рис.1.
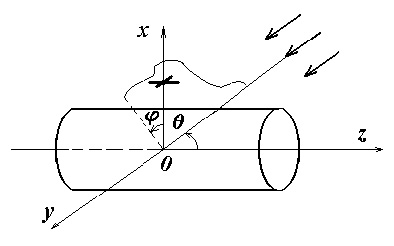
Рис.1.
Геометрия задачи.
С использованием известных
интегральных соотношений ДН
крестообразного излучателя определяется
выражением
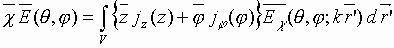 . .
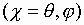
|
(1) |
В соотношении (1)
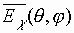 - решение в точке с радиус-вектором
- решение в точке с радиус-вектором 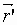 задачи дифракции плоской электромагнитной
волны на импедансном круговом цилиндре
радиуса
задачи дифракции плоской электромагнитной
волны на импедансном круговом цилиндре
радиуса 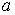 ,
приходящей с направления
,
приходящей с направления 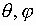 ,
вектор
,
вектор 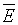 во фронте которой имеет только
во фронте которой имеет только 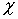 -компоненту;
-компоненту;
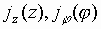 - распределения стороннего тока в плечах
крестообразного вибратора;
- распределения стороннего тока в плечах
крестообразного вибратора; 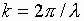 - волновое число;
- волновое число; 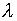 - длина волны в свободном пространстве.
Зависимость всех величин от времени,
определяемая множителем
- длина волны в свободном пространстве.
Зависимость всех величин от времени,
определяемая множителем 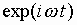 ,
здесь и в дальнейшем опущена.
,
здесь и в дальнейшем опущена.
Поскольку электродинамические и
геометрические параметры цилиндра не
зависят от координаты
z,
решение задачи будем искать в
предположении, что рассеянное поле имеет
такую же зависимость от координаты z,
как и в падающей волне, т.е. в
квазитрехмерном приближении [9,
10].
Падающее поле при таком подходе может быть
описано соотношением
|
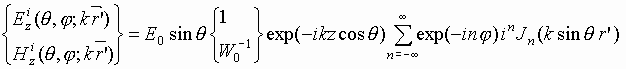 , ,
|
(2) |
в котором верхняя и нижняя строки
соответствуют случаям вычисления
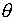 -
и
-
и 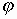 -
компонент ДН;
-
компонент ДН; 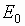 - амплитуда электрического поля во фронте
падающей волны;
- амплитуда электрического поля во фронте
падающей волны; 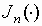 - функция Бесселя
- функция Бесселя 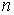 -го
порядка;
-го
порядка; 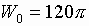 Ом.
Ом.
Поскольку сигнал произвольной
поляризации может быть представлен в виде
суперпозиции двух линейно поляризованных
колебаний, достаточно рассмотреть случай,
когда в падающей волне продольную
компоненту имеет только вектор
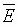 или вектор
или вектор 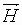 .
Однако в рассеянном поле для импедансной
поверхности, как показано в [9-11],
продольную компоненту имеют уже оба поля.
.
Однако в рассеянном поле для импедансной
поверхности, как показано в [9-11],
продольную компоненту имеют уже оба поля.
Продольные компоненты
рассеянного поля будем искать в виде
|
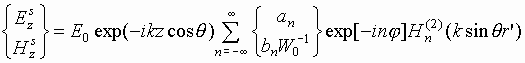 , ,
|
(3) |
где
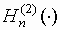 - функция Ганкеля 2-го рода n-го
порядка.
- функция Ганкеля 2-го рода n-го
порядка.
Поперечные компоненты
электромагнитного поля могут быть
определены с использованием соотношений [11]
На
поверхности кругового цилиндра 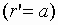 должны выполнять импедансные граничные
условия вида [9]
должны выполнять импедансные граничные
условия вида [9]
|
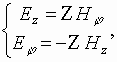
|
(5) |
где
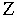 - величина поверхностного импеданса.
- величина поверхностного импеданса.
При дифракции
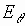 -волны
обозначим через
-волны
обозначим через 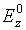 продольную компоненту напряженности
полного электрического поля, а через
продольную компоненту напряженности
полного электрического поля, а через 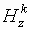 – продольную кросс поляризационную
компоненту напряженности рассеянного
магнитного поля (в падающем поле данная
компонента равна нулю). При дифракции
– продольную кросс поляризационную
компоненту напряженности рассеянного
магнитного поля (в падающем поле данная
компонента равна нулю). При дифракции 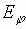 -волны
(
-волны
(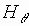 -поляризация)
через
-поляризация)
через 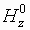 обозначим
продольную компоненту напряженности
полного магнитного поля, а через
обозначим
продольную компоненту напряженности
полного магнитного поля, а через 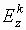 – продольную
компоненту напряженности рассеянного
электрического поля (в падающем поле данная
компонента равна нулю). После введения
данных обозначений полные поля задач
дифракции могут быть
записаны в виде
– продольную
компоненту напряженности рассеянного
электрического поля (в падающем поле данная
компонента равна нулю). После введения
данных обозначений полные поля задач
дифракции могут быть
записаны в виде
|
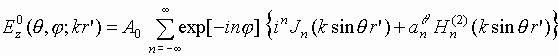
|
(6) |
|
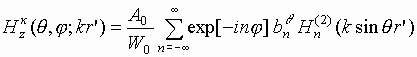
|
(7) |
для
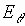 -волны
и
-волны
и
|
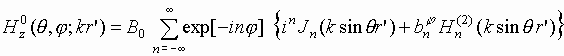
|
(8) |
|
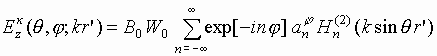
|
(9) |
для
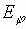 -волны
(
-волны
(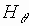 -поляризация).
-поляризация).
В соотношениях (6)-(9)
введены обозначения:
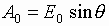 ;
;
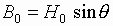 . Используя
результаты работ [12, 13],
запишем выражения для коэффициентов
. Используя
результаты работ [12, 13],
запишем выражения для коэффициентов 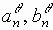 и
и 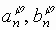 в следующем виде:
в следующем виде:
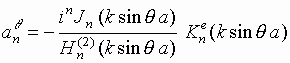
;
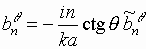 ;
;
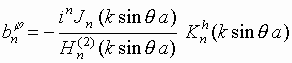 ;
;
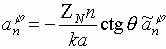 ;
;
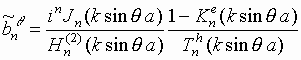 ;
; 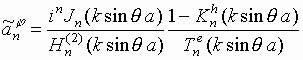 ;
;
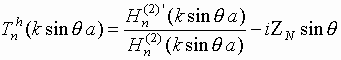 ;
;
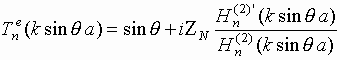 ;
;
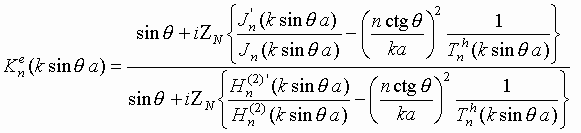
;
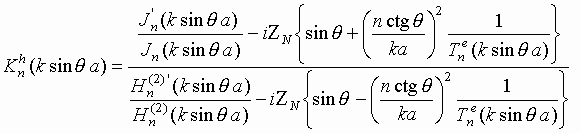
;
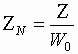 –
–
нормированный
поверхностный импеданс; 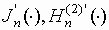 – производные
функции Бесселя n-го
порядка и Ганкеля 2-го рода n-го
порядка соответственно.
– производные
функции Бесселя n-го
порядка и Ганкеля 2-го рода n-го
порядка соответственно.
Подстановка выражений (4),
(6)-(9) в соотношение (1)
позволяет записать
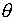 -
и
-
и 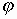 -компоненты
ДН крестообразного излучателя в виде
-компоненты
ДН крестообразного излучателя в виде
|
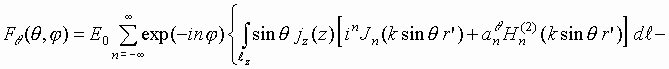
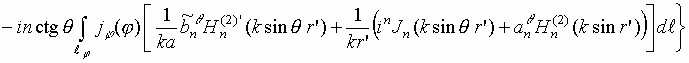 , ,
|
(10) |
|
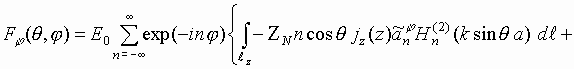
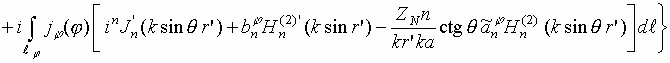 . .
|
(11) |
Формулы (10), (11)
при известном законе распределения тока в
излучателе полностью описывают
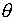 -
и
-
и 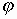 -компоненты
векторной диаграммы направленности
крестообразного вибратора, расположенного
вблизи импедансного кругового цилиндра. На
основе данных выражений несложно
определить и поляризационные
характеристики излучателя.
-компоненты
векторной диаграммы направленности
крестообразного вибратора, расположенного
вблизи импедансного кругового цилиндра. На
основе данных выражений несложно
определить и поляризационные
характеристики излучателя.
Для того, чтобы выявить
закономерности, связанные только с
влиянием импедансных свойств поверхности
цилиндра на характеристики излучения
крестообразного вибратора, в исследованиях
рассматривался случай вибратора с плечом
малой длины (крестообразный диполь). В этом
случае токи в плечах излучателя
описываются законами
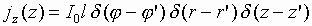 ;
;
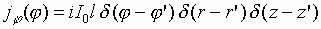 ,
,
в которых
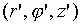 - координаты центра крестообразного
вибратора;
- координаты центра крестообразного
вибратора; 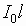 - электрический момент каждой пары плеч
излучателя.
- электрический момент каждой пары плеч
излучателя.
Значения нормированного
поверхностного импеданса
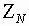 ,
как показано в [4, 12],
определяются соотношением
,
как показано в [4, 12],
определяются соотношением
|
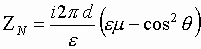 , ,
|
(12) |
где
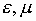 - относительные диэлектрическая и
магнитная проницаемости используемого
диэлектрического материала, наносимого на
металлический круговой цилиндр; d
– толщина покрытия.
- относительные диэлектрическая и
магнитная проницаемости используемого
диэлектрического материала, наносимого на
металлический круговой цилиндр; d
– толщина покрытия.
Результаты исследования
диаграммы направленности по мощности
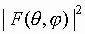 и
коэффициента эллиптичности
и
коэффициента эллиптичности 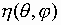 в зависимости от толщины покрытия и радиуса
кругового цилиндра приведены на рис.2-7.
Кривые с номером 1 соответствуют случаю
идеально проводящей поверхности цилиндра;
кривые с номерами 2 и 3 – при нанесении
диэлектрического покрытия с параметрами [14]:
в зависимости от толщины покрытия и радиуса
кругового цилиндра приведены на рис.2-7.
Кривые с номером 1 соответствуют случаю
идеально проводящей поверхности цилиндра;
кривые с номерами 2 и 3 – при нанесении
диэлектрического покрытия с параметрами [14]:
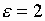 ;
; 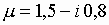 ,
,
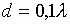 и
и
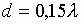 соответственно.
Значения всех
диаграмм направленности нормированы к
случаю идеально проводящей поверхности.
Удаление излучателя от поверхности
цилиндра во всех случаях принимался равным
соответственно.
Значения всех
диаграмм направленности нормированы к
случаю идеально проводящей поверхности.
Удаление излучателя от поверхности
цилиндра во всех случаях принимался равным 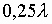 .
Рис. 2, 3 иллюстрируют
поведение характеристик излучения
крестообразного вибратора при радиусе
цилиндра
.
Рис. 2, 3 иллюстрируют
поведение характеристик излучения
крестообразного вибратора при радиусе
цилиндра 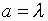 ,
рис.4, 5 – при
,
рис.4, 5 – при 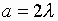 ,
рис. 6, 7 – при
,
рис. 6, 7 – при 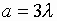 .
.
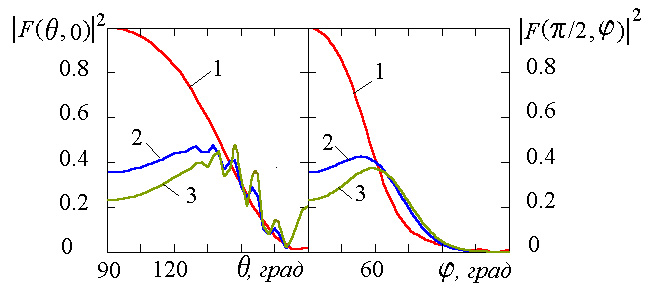
Рис.2. Зависимость диаграммы
направленности от толщины
диэлектрического покрытия
d
при 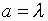
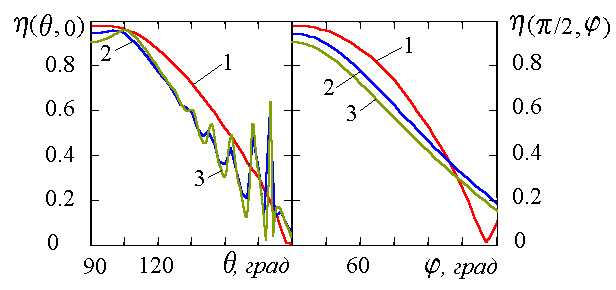
Рис.3. Зависимость коэффициента
эллиптичности от толщины
диэлектрического покрытия
d
при 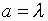
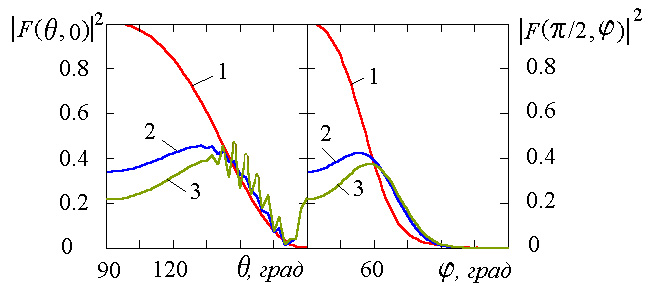
Рис.4. Зависимость диаграммы
направленности от толщины
диэлектрического покрытия
d
при 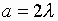
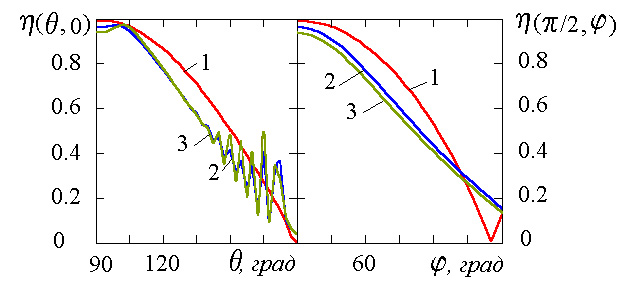
Рис.5. Зависимость коэффициента
эллиптичности от толщины
диэлектрического покрытия
d
при 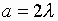
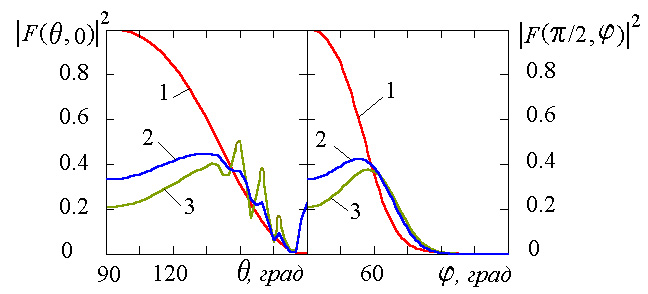
Рис.6. Зависимость диаграммы
направленности от толщины
диэлектрического покрытия
d
при 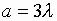
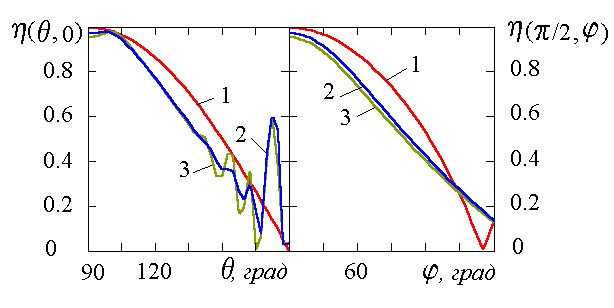
Рис.7. Зависимость коэффициента
эллиптичности от толщины
диэлектрического покрытия
d
при 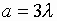
На указанных рисунках левое поле
определяет зависимость диаграммы
направленности и коэффициента
эллиптичности от угла
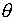 при фиксированном значении угла
при фиксированном значении угла 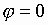 .
Правое поле – зависимость от угла
.
Правое поле – зависимость от угла 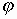 при фиксированном значении угла
при фиксированном значении угла 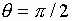 .
.
Как следует из приведенных
результатов, появление импедансных свойств
приводит к значительным изменениям
диаграммы направленности в обоих сечениях.
В меньшей степени наличие импеданса
сказывается на коэффициенте эллиптичности.
Однако при направлениях, близких к осевому,
в угломестных сечениях
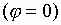 как для диаграммы направленности, так и для
коэффициента эллиптичности, наблюдаются
резкие осцилляции. Причем с увеличением
радиуса цилиндра размах осцилляций
возрастает. В поперечной плоскости
как для диаграммы направленности, так и для
коэффициента эллиптичности, наблюдаются
резкие осцилляции. Причем с увеличением
радиуса цилиндра размах осцилляций
возрастает. В поперечной плоскости 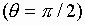 поведение данных характеристик имеет
гладкий монотонный характер. В то же время,
несмотря на сохранение общего характера
поведения коэффициента эллиптичности,
могут наблюдаться значительные
количественные изменения, достигающие
величины порядка 30%. Это проявляется в
сужении области, в которой
поведение данных характеристик имеет
гладкий монотонный характер. В то же время,
несмотря на сохранение общего характера
поведения коэффициента эллиптичности,
могут наблюдаться значительные
количественные изменения, достигающие
величины порядка 30%. Это проявляется в
сужении области, в которой 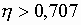 с
с 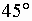 (для идеально проводящей поверхности) до
(для идеально проводящей поверхности) до 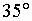 (для импедансной поверхности).
(для импедансной поверхности).
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
- Звягинцев А.А., Батраков Д.О.
Дифракция на эллиптическом импедансном
цилиндре // Изв. вуз. Радиофизика. 1981. Т.32.
№9. С.1125-1131.
- Звягинцев А.А., Батраков Д.О.
Деполяризация сигналов при
взаимодействии цилиндрических
импедансных поверхностей // Отобр. и обраб.
инф. (Киев). 1989. №4. С.65-68.
Smith T.M., Borison S.L. Depolarization of a circularly
polarized wave by an infinite cylinder // IEEE Trans. Antennas and Propag.
V.AP-22. 1974. №6.
P.796-798.
Graglia R.D., Uslenghi P.L.E., Vitiello R., D’Elia U.
Electromagnetic scattering for oblique incidence on impedance bodies of
revolution // IEEE Trans. Antennas and Propag. 1995. V.43. №1.
P.11-26.
Kumar A., Shastry S.V.K. Radiation from dipoles in the
presence of dielectric-coated circular cylinder // “J. Inst. Electron. And
Telecommun. Eng.”. 1985. V.31. №6.
P.184-189.
Кашин А.В., Соловьев В.М.
Исследование малогабаритной
слабонаправленной антенны, расположенной
на круговой цилиндрической поверхности //
Изв. вуз. Радиоэлектроника. 1982. Т.25. №2. С.78-80.
Васильев Е.Н. Возбуждение тел
вращения. – М.: Радио и связь, 1987. – 272с.
Айзенберг Г.З., Ямпольский В.Г.,
Терешин О.Н. Антенны УКВ /Под ред. Г.З.
Айзенберга в 2-х частях. Ч.1. – М.: Связь, 1977.
– 384с.
Ваганов Р.Б., Каценеленбаум Б.З.
Основы теории дифракции. – М.: Наука, 1982. - с.
Баранчугов Е.А., Зацепин П.М.,
Комаров С.А. Квазитрехмерная задача
дифракции плоской электромагнитной волны
на импедансной ленте // Радиотехника и
электроника. Т.43. 1998. №11. С.1291-1295.
Уэйт Д.Р. Электромагнитное
излучение из цилиндрических систем. – М.:
Сов. радио, 1963. – 239с.
Zvezdina M.Yu., Stepanov A.S., Kharchenko V.V., Chernov S.V.
Scattering plane electromagnetic wave by impedance circular cylinder // Proc.
of 3rd Int. Conf. Antenna Theory and Techniq., Sevastopil, Ukraine,
8-11 Sept. 1999, P.173-175.
Gabriel’yan D.D., Zvezdina M.Yu. The influence of
impedance surface of a circular cylinder on the dipole pattern // Proc. of 3rd
Int. Conf. Antenna Theory and Techniq., Sevastopil, Ukraine, 8-11 Sept. 1999,
P.113-115.
Халлиулин Д.Я., Третьяков С.А.
Обобщенные граничные условия
импедансного типа для тонких плоских
слоев различных сред (обзор) //
Радиотехника и электроника. 1998. Т.43. №1. С.16-29.
Авторы:
Габриэльян Дмитрий Давидович – д.т.н. с.н.с.,
РВИ РВ,
Звездина Марина Юрьевна – к.т.н., РВИ РВ,
zvezd@jeo.ru
Костенко Петр Иванович – РВИ РВ.
![]() - функция Ганкеля 2-го рода n-го
порядка.
- функция Ганкеля 2-го рода n-го
порядка.![]() -волны
и
-волны
и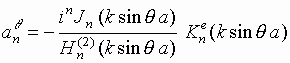
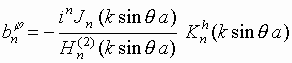 ;
; 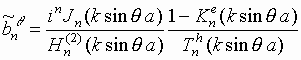 ;
; 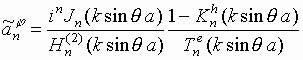 ;
;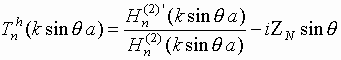 ;
;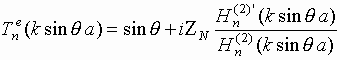 ;
;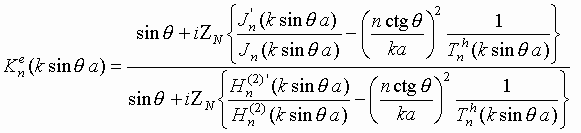
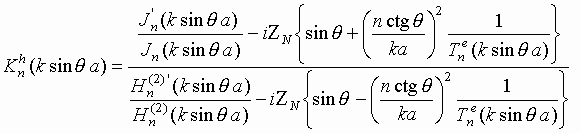
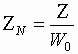 –
– ![]() ;
;
![]() ,
,