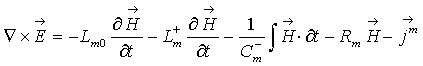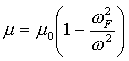| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 2, 2001 |
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДЛЯ РЕШЕНИЯ ЗАДАЧ РАССЕЯНИЯ ЭЛЕКТРОМАГНИТНЫХ
ВОЛН ВО ВРЕМЕННОЙ ОБЛАСТИ
К. Н. Климов*, Б. В. Сестрорецкий**
*Московский государственный институт электроники и
математики
**ПНО им. Лавочкина
Получена
3 февраля 2001 г.
Предложена модификация дифференциальных уравнений Максвелла, позволяющая формировать алгоритмы для анализа во временной области систем с произвольным распределением и заданной частотной дисперсией диэлектрической и магнитной проницаемостей. Построенные на основе полученных уравнений алгоритмы обладают численной устойчивостью при положительных, отрицательных и равных нулю значениях диэлектрической и магнитной проницаемостей.
Как известно, уравнения Максвелла в дифференциальной форме записываются следующим образом:
Для изотропного диэлектрика материальные уравнения среды:
Удобно уравнения (1) и (2) записать в следующем виде:
В символическом виде :
где  - символическая форма
записи оператора дифференцирования по времени,
- символическая форма
записи оператора дифференцирования по времени, ![]() - удельная
эквивалентная электрическая емкость,
- удельная
эквивалентная электрическая емкость, ![]() - удельная
эквивалентная магнитная индуктивность.
- удельная
эквивалентная магнитная индуктивность.
Система уравнений (4) представляет из себя систему эквивалентную трехмерному телеграфному уравнению, записанному в инвариантной относительно системы координат форме. В случае, если диэлектрическая и магнитная проницаемости являются тензорами и зависят от частоты, то (4) можно записать в виде:
где ![]() тензор удельной
электрической проводимости, характеризующий свойства вакуума и среды по
электрическому полю,
тензор удельной
электрической проводимости, характеризующий свойства вакуума и среды по
электрическому полю, ![]() тензор удельного
магнитного сопротивления, характеризующий свойства вакуума и среды для
магнитного поля.
тензор удельного
магнитного сопротивления, характеризующий свойства вакуума и среды для
магнитного поля.
Элементами тензора удельной электрической проводимости ![]() являются
интегро-дифференциальные операторы, которые удобно записать в символическом
виде как функции относительно
являются
интегро-дифференциальные операторы, которые удобно записать в символическом
виде как функции относительно ![]() :
: ![]() . Элементами тензора удельного магнитного сопротивления
. Элементами тензора удельного магнитного сопротивления ![]() также являются
интегро-дифференциальные операторы, которые запишем в символическом виде как
функции относительно
также являются
интегро-дифференциальные операторы, которые запишем в символическом виде как
функции относительно ![]() следующим образом:
следующим образом: ![]() . При такой записи введены обозначения:
. При такой записи введены обозначения: 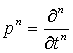 - символическая форма
записи оператора дифференцирования порядка
- символическая форма
записи оператора дифференцирования порядка ![]() по времени, а
по времени, а 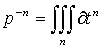 - символическая форма
записи оператора интегрирования порядка
- символическая форма
записи оператора интегрирования порядка ![]() по времени.
по времени.
Для описания свойств веществ при ![]() (
(![]() ) удобнее было бы пользоваться не
) удобнее было бы пользоваться не ![]() (
(![]() ), а величинами
), а величинами ![]() (
(![]() ) [1]. В частном случае для описания свойств плазмы в случае
без столкновений или ферритов, можно записать уравнения
(5) в виде:
) [1]. В частном случае для описания свойств плазмы в случае
без столкновений или ферритов, можно записать уравнения
(5) в виде:
где ![]() - удельная
электрическая емкость вакуума;
- удельная
электрическая емкость вакуума; ![]() - удельная магнитная
индуктивность вакуума;
- удельная магнитная
индуктивность вакуума; ![]() - удельная
электрическая емкость вещества, увеличивающая емкость вакуума;
- удельная
электрическая емкость вещества, увеличивающая емкость вакуума; ![]() - удельная магнитная
индуктивность вещества, увеличивающая индуктивность вакуума;
- удельная магнитная
индуктивность вещества, увеличивающая индуктивность вакуума; ![]() - удельная магнитная
емкость вещества , уменьшающая индуктивность вакуума;
- удельная магнитная
емкость вещества , уменьшающая индуктивность вакуума; ![]() - удельная
электрическая индуктивность вещества, уменьшающая емкость вакуума;
- удельная
электрическая индуктивность вещества, уменьшающая емкость вакуума; ![]() - удельные
электрические;
- удельные
электрические; ![]() - удельные магнитные
потери.
- удельные магнитные
потери.
Уравнение
(6) , записанное для монохроматических колебаний с заданной
круговой частотой ![]() , дает известное выражение для плазмы
[2] , из которого
определяется частотная зависимость диэлектрической проницаемости:
, дает известное выражение для плазмы
[2] , из которого
определяется частотная зависимость диэлектрической проницаемости:
где 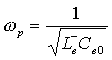 .
.
Аналогично известная частотная зависимость [3] получается и для магнитной проницаемости ферритов из уравнения (7) :
где 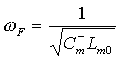 .
.
Полученные уравнения (6) и (7) позволили построить вычислительно устойчивые процедуры анализа на основе аппарата импедансных сеток [4,5] для интерпретации результатов экспериментов по рассеянию электромагнитных волн от горячей замагниченной плазмы в установках ТОКАМАК [6].
ПРОГРАММНАЯ РЕАЛИЗАЦИЯ
Алгоритм анализа рассеяния электромагнитных волн во временной области на основе уравнений (6) и (7) двумерных задач реализован в программе PlanarRt-Hanalyzer для волн H поляризации [5] и в программе PlanarRt-Eanalyzer для волн E поляризации [7]. Программы PlanarRt-Hanalyzer и PlanarRt-Eanalyzer оптимизированы под систему команд процессора Pentium-II и выше.
В программе PlanarRt-Hanalyzer расход памяти составляет четыре вещественных числа на узел. Количество арифметических операций в один временной такт для одного узла сетки составляет: четыре сложения, два умножения и одно вычитание вещественных чисел. Теоретически данный алгоритм требует 25 процессорных тактов для одного узла сетки, однако, реально получается почти в два раза больше, что обусловлено более низкой рабочей частотой шины данных и кэш памяти. Например, если тактовая частота процессора составляет 433 МГц, то частота шины данных (по которой идёт обмен данных между оперативной памятью и процессором ) составляет 100 МГц, а частота работы кэш памяти второго уровня (основной объём кэш памяти) – 217 МГц.
Программа PlanarRt-Hanalyzer реализована в двух
моделях:1) одинарная точность – вещественные числа занимают 4 байта (мантисса
имеет 7 цифр, порядок от –38 до +38); 2) двойная точность – вещественные числа
занимают 8 байт (мантисса имеет 15 цифр, порядок от –308 до +308). Основные
параметры: 16 байт памяти на узел сетки, 48 тактов процессора на узел при
одинарной точности; 32 байт на узел и 78 тактов процессора на узел при двойной
точности анализа. Например, при одинарной точности расчета объекты с размером
![]() анализируются на
компьютере Pentium-II 433МГц с оперативной памятью 512 Мб ( программа
использует 164.8Мб ) за время 15 часов (при шаге сетки, равном
анализируются на
компьютере Pentium-II 433МГц с оперативной памятью 512 Мб ( программа
использует 164.8Мб ) за время 15 часов (при шаге сетки, равном ![]() устройство
разбивается на 10 800 000 узлов). При этом осуществляется просмотр 5 проходов
волны вдоль размера, составляющего
устройство
разбивается на 10 800 000 узлов). При этом осуществляется просмотр 5 проходов
волны вдоль размера, составляющего ![]() , за 45000 временных тактов.
, за 45000 временных тактов.
В программе PlanarRt-Eanalyzer расход памяти
составляет шесть вещественных чисел на один узел импедансной сетки. Число
арифметических операций в один временной такт для одного узла составляет:
восемь сложений - вычитаний и восемь умножений вещественных чисел. Программа PlanarRt-Eanalyzer также реализована в двух
моделях: одинарная и двойная точность. Основные параметры: 28 байтов памяти на
узел сетки, 72 тактов процессора на узел при одинарной точности; 56 байтов
памяти и 117 тактов процессора на узел при двойной точности анализа. Например,
при одинарной точности расчета объекты с размером ![]() анализируются на
компьютере Pentium-II 433 МГц с оперативной памятью 512 Мб (программа
использует 288.4 Мб) за время 22.5 часов (при шаге сетки, равном
анализируются на
компьютере Pentium-II 433 МГц с оперативной памятью 512 Мб (программа
использует 288.4 Мб) за время 22.5 часов (при шаге сетки, равном ![]() устройство
разбивается на 10 800 000 узлов). При этом осуществляется просмотр пяти
проходов волны вдоль размера, составляющего
устройство
разбивается на 10 800 000 узлов). При этом осуществляется просмотр пяти
проходов волны вдоль размера, составляющего ![]() , за 45000 временных тактов.
, за 45000 временных тактов.
Программы PlanarRt-Hanalyzer и PlanarRt-Eanalyzer позволяют наблюдать результаты расчёта картин распределения электромагнитного поля в анимационном режиме и сигналы на входах устройства. Имеющаяся реализация программ позволяет работать с ними на компьютерах, объединённых в локальную сеть, распределяя процессы между ресурсами компьютеров.
РАССЕЯНИЕ РАДИОИМПУЛЬСА НА ЦИЛИНДРЕ С НЕОДНОРОДНЫМ ДИЭЛЕКТРИЧЕСКИМ ЗАПОЛНЕНИЕМ
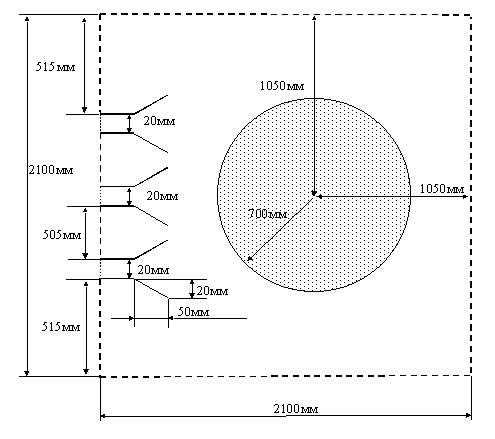
В качестве примера приведем результаты анализа геометрии изображенной на рис. 1 с помощью программы PlanarRt-Hanalyzer. Исследуемая система состоит из трех рупоров и неоднородного диэлектрического цилиндра радиуса 700 мм, диэлектрическая проницаемость которого линейно зависит от радиуса рупоров подключены на границе цилиндра равна 1, а в центре - минус 1 на частоте 10 ГГц, а на других частотах определяется в соответствии с выражением (8) . К входам прямоугольные волноводы шириной 20мм. Область анализа – прямоугольник, ограниченный поглотителем.
Пусть нижний рупор будет излучающим, а центральный и верхний рупора -
приемными. Анализ проведем для радиоимпульса длительностью ![]() секунд, с частотой
заполнения 10 ГГц.
секунд, с частотой
заполнения 10 ГГц.
Рис. 1. Геометрия задачи рассеяния на цилиндре неоднородным диэлектрическим заполнением.
Шаг дискретизации сетки возьмем 2мм. Это соответствует 1/15 длины волны в свободном пространстве. При этом ошибка фазы на одну длину волны будет составлять 1.341° или 0.372% [4]. Вся область анализа составит 70 на 70 длин волн. Импедансная сетка будет состоять из 1104601 узлов. На компьютере Pentium-II 433 МГц для программы с одинарной точностью потребуется менее 17 Мб оперативной памяти и менее 8.5 минут для анализа на временном интервале 20 нс.
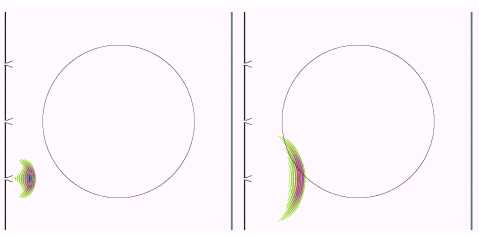
На рис. 2 показано распределение интенсивности поля ![]() для следующих
моментов времени: 1, 2, 3, 4, 5 и 6 нс.
для следующих
моментов времени: 1, 2, 3, 4, 5 и 6 нс.
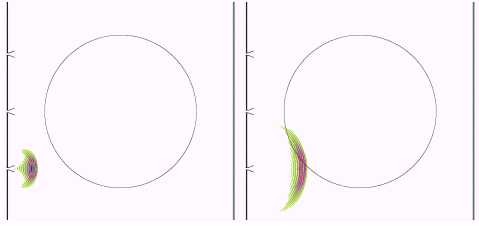
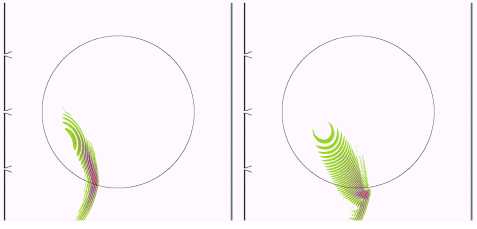
Рис. 2. Распределение амплитуды ![]() в моменты времени 1,
2, 3, 4, 5 и 6 нс.
в моменты времени 1,
2, 3, 4, 5 и 6 нс.
ЗАКЛЮЧЕНИЕ
Построенные на основе уравнений (6) и (7) алгоритмы анализа во временной области, как показано в [5,7], обладают численной устойчивостью при положительных, отрицательных и равных нулю значениях диэлектрической и магнитной проницаемостей. Причем при анализе рассеяния сигналов с широким спектром учитывается частотная зависимость диэлектрических и магнитных свойств среды вида (8) и (9).
СПИСОК ЛИТЕРАТУРЫ
1. Климов К.Н., Сестрорецкий Б.В. // РЭ. Т. 46. 2001. N1. С. 30.
2. Клеммоу С., Тоуэрти Дж. Электродинамика частиц и плазмы. М.: Мир, 1996. С. 526.
3. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. - М.: Наука, 1994. С. 464.
4. K.N. Klimov, B.V. Sestroretzkiy, S.V. Soldatov. The analysis of planar structures with any distribution of permittivity in time domain mode // Proceeding of 2000 International Conference on Mathematical Methods in Electromagnetic Theory. Vol. 1, Kharkov, Ukraine, September, 12-15, 2000, P 128.
5. Сестрорецкий Б.В., Петров
А.С., Иванов С.А. и др. Анализ электромагнитных процессов на основе ![]() - и
- и ![]() - сеток. - М.: МГИЭМ, 2000. С. 149.
- сеток. - М.: МГИЭМ, 2000. С. 149.
6. V.A. Vershkov, V.V. Dreval, S.V. Soldatov. // Rev. Sci. Instr. V. 70. 1999. N3. P 1700.
7. Климов К.Н., Сестрорецкий Б.В. // Сборник трудов научно-технической конференции "ЭМС и интеллектуальные здания". Москва, Россия, 13-14 Декабря, 2000, С. 69.
Авторы:
1. Климов Константин
Николаевич, 1969 г.р. Ассистент кафедры РТУиС
Радиотехнического факультета
Московского государственного института электроники и математики. Область
научных интересов: создание алгоритмов и программ электродинамического анализа
для проектирования СВЧ трактов и антенн, проектирование СВЧ устройств.
E-mail: const0@online.ru
2. Сестрорецкий Борис
Васильевич, 1923 г.р. Доктор технических наук,
Главный специалист ПНО им.
Лавочкина. Область научных интересов: вычислительная электродинамика, создание
алгоритмов и промышленных программ электродинамического анализа для проектирования
СВЧ трактов и антенн, проектирование СВЧ устройств и антенн.
E-mail: const0@online.ru
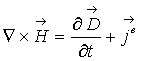
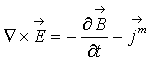 (1)
(1)
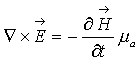 (3)
(3)