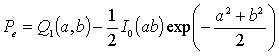|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 2, 2002 |
|
ПОМЕХОУСТОЙЧИВОСТЬ МОДЕМОВ СО МНОГИМИ НЕСУЩИМИ ПРИ ГЛАДКИХ НЕЛИНЕЙНЫХ ИСКАЖЕНИЯХ В ВЫСОКОЧАСТОТНЫХ КАСКАДАХ АППАРАТУРЫ СВЯЗИ
Жидков С.В.
Ижевский государственный технический университет
Получена 27 января 2002 г.
В работе рассмотрена методика аналитического расчета помехоустойчивости модемов со многими несущими (ММН) при нелинейных искажениях в высокочастотных каскадах аппаратуры связи. Получены аналитические выражения, позволяющие рассчитать эквивалентное отношение сигнал/помеха для каждой поднесущей группового сигнала ММН. Рассмотрены вопросы оценки помехоустойчивости систем с малым числом поднесущих. Приведены результаты моделирования и расчетов помехоустойчивости ММН-модемов с относительной фазовой манипуляцией.
1. Введение
3. Расчет эквивалентного отношения сигнал/помеха
4. Распределение квадратурных составляющих помехи
6. Заключение
7. Литература
В последние годы широкое распространение в цифровой радиосвязи получила техника модуляции со многими несущими (ММН) [1]. Популярность ММН обусловлена устойчивостью этого вида модуляции к многолучевому распространению радиоволн и эффективностью программно-аппаратной реализации ММН-модемов [2]. Наряду с указанными достоинствами ММН обладает недостатками, основным из которых является высокая чувствительность к нелинейным искажениям, возникающим в радиотрактах аппаратуры связи. При прохождении группового сигнала ММН через нелинейные каскады нарушается ортогональность поднесущих, что приводит к их взаимному влиянию и, в конечном итоге, к снижению помехоустойчивости цифровой передачи.
Большинство работ, посвященных изучению помехоустойчивости ММН-модемов в условиях нелинейных искажений, базируются на методах имитационного моделирования [3, 4]. Однако, результаты этих исследований носят частный характер и не позволяют сделать важные обобщающие выводы. Более глубокий взгляд на проблему дан в работах [5, 6], где проведена попытка аналитической оценки влияния нелинейных искажений произвольного характера на помехоустойчивость ММН. Исследования [5, 6] базируются на том факте, что при достаточно большом числе поднесущих комплексная огибающая группового сигнала ММН носит гауссовский характер. Такое допущение позволяет применить для анализа помехоустойчивости ММН хорошо развитую теорию нелинейных преобразований гауссовских процессов [7].
В то же время существует ряд приложений, в которых по техническим или иным соображениям количество поднесущих при ММН ограничено. Одним из примеров таких приложений являются модемы для декаметровой радиосвязи [8, 9]. Обычно число поднесущих в подобных системах составляет от 8 до 64, поэтому предположение о гауссовском характере огибающей сигнала ММН является, строго говоря, некорректным. Помимо сказанного следует отметить, что методики расчетов изложенные в [5, 6], отличаются громоздкостью вычислений и плохо подходят для инженерного анализа.
Настоящая работа посвящена исследованию влияния нелинейных искажений на работу ММН-модемов при произвольном числе поднесущих. В отличие от работ [5, 6], в данном исследовании мы исходим из того, что при ММН поднесущие расположены на одинаковом расстоянии друг от друга, поэтому все комбинационные составляющие либо точно совпадают с частотой одной из поднесущих, либо находятся вне полосы сигнала ММН. Как будет показано далее, этот факт позволяет точно рассчитать отношение энергии полезной составляющей к суммарной энергии продуктов нелинейных искажений для каждой поднесущей сигнала ММН. На основе полученных соотношений в работе предложена методика практического анализа помехоустойчивости систем с ММН и проведено сравнение теоретических результатов с результатами имитационного моделирования.
При ММН групповой сигнал модема на интервале передачи одного символа может быть представлен в виде
где
![]() –
центральная частота группового сигнала,
–
центральная частота группового сигнала,
N
– количество поднесущих,
![]() – разнос частот между поднесущими,
– разнос частот между поднесущими,
Uk
– амплитуда k-й
поднесущей,
![]() –
текущая фаза k-й
поднесущей,
–
текущая фаза k-й
поднесущей,
T
– длительность символьного интервала.
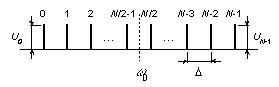
Схематичное представление сигнала ММН в
частотной области иллюстрируется рис. 1. Амплитуды (Uk)
и фазы (![]() ) группового сигнала (1) определяются характером
модуляции и информацией, передаваемой по каналу связи. Например, при передаче
сигналов с фазовой модуляцией амплитуды являются константами, а фазы –
случайными величинами. Статистические свойства ансамбля величин
) группового сигнала (1) определяются характером
модуляции и информацией, передаваемой по каналу связи. Например, при передаче
сигналов с фазовой модуляцией амплитуды являются константами, а фазы –
случайными величинами. Статистические свойства ансамбля величин
![]() определяются характером
передаваемой информации. Если источник информации имеет высокую
энтропию, и в системе не используется помехоустойчивое кодирование, то
случайные величины
определяются характером
передаваемой информации. Если источник информации имеет высокую
энтропию, и в системе не используется помехоустойчивое кодирование, то
случайные величины
![]() можно считать независимыми и
равномерно распределенными на интервале
можно считать независимыми и
равномерно распределенными на интервале
![]() .
.
Рис. 1. Спектр сигнала ММН (при четном N)
Нелинейные искажения сигнала ММН в аппаратуре
связи возникают в основном из-за нелинейности статических и динамических
характеристик высокочастотных усилительных приборов [10, 11].
Далее мы рассмотрим модель нелинейного тракта в виде безынерционного
четырехполюсника с нелинейной проходной характеристикой
![]() и
выходного полосового фильтра.
и
выходного полосового фильтра.
Количественную оценку нелинейности радиотракта обычно получают, оценивая
степень искажения специального тестового сигнала. В качестве такого сигнала
чаще всего применяется двухчастотный равноамплитудный сигнал
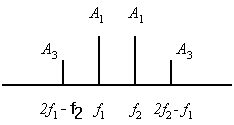
[11, 12]. При прохождении двухчастотного сигнала через нелинейный каскад в
спектре, кроме двух составляющих появляются дополнительные компоненты
A3 (см. рис.2).
Измерение уровня этих компонент и вычисление коэффициента нелинейных искажений
(КНИ) третьего порядка
![]() лежит
в основе большинства практических методик оценки нелинейности радиотрактов. По
аналогии можно определить КНИ более высоких порядков (пятого, седьмого и
т.д.), однако, на практике эти показатели применяются сравнительно редко, так
как в большинстве случаев искажения третьего порядка являются доминирующими
[11].
лежит
в основе большинства практических методик оценки нелинейности радиотрактов. По
аналогии можно определить КНИ более высоких порядков (пятого, седьмого и
т.д.), однако, на практике эти показатели применяются сравнительно редко, так
как в большинстве случаев искажения третьего порядка являются доминирующими
[11].
Рис. 2. Спектр двухчастотного сигнала при нелинейных искажениях третьего порядка
В случае гладких искажений проходная характеристика безынерционной части схемы может быть представлена в виде степенного ряда с ограниченным числом членов [10]:
Если нелинейные искажения третьего порядка являются доминирующими, то проходная характеристика (2) может быть адекватно представлена всего четырьмя членами (M=3). При таком математическом представлении модели нелинейного тракта КНИ третьего порядка можно выразить через параметры модели [11]:
где U2t – амплитуда составляющих тестового двухчастотного сигнала.
Влияние нелинейных искажений указанного типа на каждую поднесущую группового сигнала ММН может быть выражено эквивалентным отношением сигнал/помеха (ОСП), под которым в дальнейшем будем подразумевать отношение энергии полезной составляющей сигнала ММН к суммарной энергии продуктов нелинейных искажений для определенной поднесущей.
3. Расчет эквивалентного отношения сигнал/помеха
Для
анализа воздействий N
гармонических сигналов на безынерционный
нелинейный элемент может быть применено несколько методов. В общем случае
такой анализ проводят с помощью разложения передаточной характеристики
![]() в
N-кратный
ряд Фурье [10]. Однако равномерное расположение поднесущих
сигнала ММН позволяет провести анализ непосредственно во временной области.
Учитывая, что сигнал на входе нелинейного усилительного прибора с
характеристикой (2) определяется выражением (1),
выходное колебание можно представить в виде
в
N-кратный
ряд Фурье [10]. Однако равномерное расположение поднесущих
сигнала ММН позволяет провести анализ непосредственно во временной области.
Учитывая, что сигнал на входе нелинейного усилительного прибора с
характеристикой (2) определяется выражением (1),
выходное колебание можно представить в виде
Раскрывая степени в (4) и применяя простейшие тригонометрические преобразования получим:
где
![]() (m=2,3)
обозначает перебор всех возможных знаков при суммировании
(m=2,3)
обозначает перебор всех возможных знаков при суммировании
![]() ,
то же самое сочетание знаков должно быть при слагаемых
,
то же самое сочетание знаков должно быть при слагаемых
![]() и
и
![]() .
В дальнейшем нас будут интересовать только те составляющие спектра, которые
находятся вблизи частоты
w0,
так как низкочастотные составляющие и гармоники частоты
w0
отфильтровываются в выходном полосовом фильтре. Несложно заметить, что
слагаемые с такими частотами будут появляться только при коэффициентах ряда (2)
с нечетными номерами m,
когда
.
В дальнейшем нас будут интересовать только те составляющие спектра, которые
находятся вблизи частоты
w0,
так как низкочастотные составляющие и гармоники частоты
w0
отфильтровываются в выходном полосовом фильтре. Несложно заметить, что
слагаемые с такими частотами будут появляться только при коэффициентах ряда (2)
с нечетными номерами m,
когда
![]() слагаемых
суммы
слагаемых
суммы
![]() имеют
положительный знак, а остальные
имеют
положительный знак, а остальные
![]() –
отрицательный. Число указанных комбинаций
–
отрицательный. Число указанных комбинаций
![]() составляет
составляет
![]() ,
поэтому колебание на выходе полосового фильтра при
,
поэтому колебание на выходе полосового фильтра при
![]() будет
определяться выражением
будет
определяться выражением
Рассмотрим наиболее важный для практики случай,
когда амплитуды поднесущих равны
![]() .
При таком условии все слагаемые в выражении (6),
соответствующие кубическому члену в переходной характеристике (2),
будут иметь одинаковое амплитудное значение, что существенно упрощает анализ.
.
При таком условии все слагаемые в выражении (6),
соответствующие кубическому члену в переходной характеристике (2),
будут иметь одинаковое амплитудное значение, что существенно упрощает анализ.
Чтобы вычислить эквивалентное ОСП на
k-й
поднесущей, прежде всего, необходимо определить количество слагаемых в
выражении (6), совпадающих с частотой
k-й
поднесущей. Число таких слагаемых будет определяться количеством комбинаций
индексов
![]() ,
для которых выполняется условие
,
для которых выполняется условие
В радиотехнике аналогичная задача возникает при анализе непараметрических обнаружителей, работающих по методу суммирования рангов наблюдений. Результаты такого анализа для общего случая приведены, например, в работе [13]. В частном случае, когда требуется определить число комбинаций Sk, удовлетворяющих условию (7), выражения, полученные в [13], могут быть приведены к виду
Далее необходимо учесть тот факт, что часть комбинационных составляющих
суммируется в фазе с полезным сигналом. Этим составляющим соответствуют
слагаемые в выражении (6), для которых выполняется условие (7)
и при этом либо
![]() ,
либо
,
либо
![]() .
Несложно заметить, что число составляющих, для которых
.
Несложно заметить, что число составляющих, для которых
![]() и
выполняется условие (7), равняется N
для любого значения k. Аналогично, количество
составляющих, для которых
и
выполняется условие (7), равняется N
для любого значения k. Аналогично, количество
составляющих, для которых
![]() и
выполняется условие (7), также будет равно
N. И только при одной комбинации индексов
выполняются оба условия одновременно (если
и
выполняется условие (7), также будет равно
N. И только при одной комбинации индексов
выполняются оба условия одновременно (если
![]() ).
Таким образом, число комбинационных составляющих Ss,
суммирующихся в фазе с сигнальным колебанием, будет определяться выражением
).
Таким образом, число комбинационных составляющих Ss,
суммирующихся в фазе с сигнальным колебанием, будет определяться выражением
независимо от номера поднесущей (k).
Из оставшихся
![]() слагаемых
формируется колебание помехи. Следует только отметить, что часть из этих
компонент суммируется некогерентно, а другая часть складывается в фазе.
Большая часть составляющих образует пары, суммирующиеся в фазе, так как каждой
комбинации вида
слагаемых
формируется колебание помехи. Следует только отметить, что часть из этих
компонент суммируется некогерентно, а другая часть складывается в фазе.
Большая часть составляющих образует пары, суммирующиеся в фазе, так как каждой
комбинации вида
![]() (
(![]() )
можно поставить в соответствие комбинацию, в которой индексы
n1 и n2
переставлены местами. Составляющие, не образующие пар, соответствуют
комбинациям вида
)
можно поставить в соответствие комбинацию, в которой индексы
n1 и n2
переставлены местами. Составляющие, не образующие пар, соответствуют
комбинациям вида
![]() ,
где
,
где
![]() .
Проще всего подсчитать число составляющих, не образующих пары (
.
Проще всего подсчитать число составляющих, не образующих пары (![]() ).
Результат легко получить, если привести условие
).
Результат легко получить, если привести условие
![]() (
(![]() )
к виду
)
к виду
При фиксированном k правая часть условия (10)
может принимать N различных значений
![]() ,
однако равенство (10) будет выполняться только в том
случае, если сумма в правой части выражения будет четной. Таким образом, при
четных N число комбинаций, удовлетворяющих условию (10),
всегда будет равно
,
однако равенство (10) будет выполняться только в том
случае, если сумма в правой части выражения будет четной. Таким образом, при
четных N число комбинаций, удовлетворяющих условию (10),
всегда будет равно
![]() независимо
от значения k. При нечетных N
– это число будет зависеть от индекса k. Если
k – четное, то число комбинаций, удовлетворяющих
условию (10), будет равно
независимо
от значения k. При нечетных N
– это число будет зависеть от индекса k. Если
k – четное, то число комбинаций, удовлетворяющих
условию (10), будет равно
![]() ,
если k – нечетное, то это число будет составлять
,
если k – нечетное, то это число будет составлять
![]() .
Из общего количества непарных слагаемых, формирующих колебание помехи, следует
исключить одну комбинацию, которая, удовлетворяя условию (10),
совпадает по фазе с полезным сигналом (
.
Из общего количества непарных слагаемых, формирующих колебание помехи, следует
исключить одну комбинацию, которая, удовлетворяя условию (10),
совпадает по фазе с полезным сигналом (![]() ).
Окончательно искомое значение
).
Окончательно искомое значение
![]() можно
представить в виде
можно
представить в виде
где mod(k,2) – обозначает
остаток от деления k на два. Тогда число когерентных
пар, формирующих колебание помехи, будет равно
![]() .
.
Используя полученные выражения несложно рассчитать эквивалентное отношение сигнал/помеха для каждой поднесущей группового сигнала ММН. Здесь удобнее всего оперировать с отношением сигнал/помеха на символ, которое в соответствии с общепринятыми методиками [1] можно определить как
где Us – амплитудное значение полезного
колебания, а
![]() –
дисперсия квадратурных составляющих суммарного колебания помехи на
k-й поднесущей. Амплитуда колебания полезного
сигнала не зависит от номера поднесущей и равняется
–
дисперсия квадратурных составляющих суммарного колебания помехи на
k-й поднесущей. Амплитуда колебания полезного
сигнала не зависит от номера поднесущей и равняется
где Ss – число слагаемых, соответствующих кубическому члену проходной характеристики (2) и суммирующихся в фазе с полезным сигналом (9).
Для определения дисперсии квадратурных составляющих помехи
![]() следует
учесть тот факт, что помеховое колебание представляет собой сумму
следует
учесть тот факт, что помеховое колебание представляет собой сумму
![]() синусоидальных
колебаний с амплитудами
синусоидальных
колебаний с амплитудами
![]() ,
и
,
и
![]() синусоидальных
колебаний с удвоенными амплитудами
синусоидальных
колебаний с удвоенными амплитудами
![]() .
Все указанные колебания имеют случайную начальную фазу и складываются
некогерентно. Так как дисперсия квадратурных составляющих синусоидальных
колебаний со случайной фазой и амплитудой
.
Все указанные колебания имеют случайную начальную фазу и складываются
некогерентно. Так как дисперсия квадратурных составляющих синусоидальных
колебаний со случайной фазой и амплитудой
![]() составляет
составляет
![]() [7],
можно записать после несложных преобразований
[7],
можно записать после несложных преобразований
где
![]() –
определяются равенствами (8), (9) и (11).
Итоговое выражение для отношения сигнал/помеха можно представить в виде:
–
определяются равенствами (8), (9) и (11).
Итоговое выражение для отношения сигнал/помеха можно представить в виде:
Для практических расчетов гораздо удобнее представить ОСП как функцию от КНИ
третьего порядка (K3), предполагая, что
дисперсии тестового двухчастотного сигнала (![]() )
и сигнала ММН (
)
и сигнала ММН (![]() )
одинаковы. Проводя в (16) замену получим:
)
одинаковы. Проводя в (16) замену получим:
где функция sign(х) возвращает знак аргумента. Из равенства (3) можно выразить отношение
где K3 – КНИ третьего порядка, выраженный
в децибелах. Подставляя этот результат в (17) и раскрывая
выражения для
![]() окончательно
получим
окончательно
получим
при четных значениях N, и
при нечетных значениях N.
Таким образом, ОСП представляет собой функцию четырех аргументов: КНИ третьего
порядка (K3),
числа поднесущих (N),
номера поднесущей (k)
и знака коэффициента a3.
Интересно заметить, что при одинаковом КНИ предпочтительнее тракт, у которого
![]() ,
так как при этом часть комбинационных составляющих (Ss)
суммируется в фазе c
сигнальным колебанием, а не вычитается из
полезного сигнала как при
,
так как при этом часть комбинационных составляющих (Ss)
суммируется в фазе c
сигнальным колебанием, а не вычитается из
полезного сигнала как при
![]() .
.
В
компактном виде можно получить выражение, для нижней границы ОСП предположив,
что число поднесущих
![]() ,
а
,
а
![]() (наихудший случай). В пределе
получим
(наихудший случай). В пределе
получим
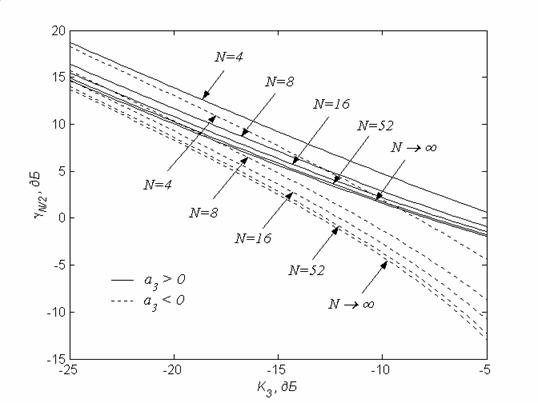
На рис.3 приведены результаты
расчетов ОСП для центральной поднесущей сигнала ММН при различных значениях
N,
sign(a3)
и K3. На этом же рисунке
показаны нижние границы, рассчитанные в соответствии с выражением (21).
Как показывают расчеты, уже при
![]() разница
между точным значением ОСП и нижней границей составляет не более 0,5 дБ.
Однако при меньших значениях
N
целесообразнее воспользоваться точными
выражениями (19) или (20). Влияние знака
a3 на ОСП особенно заметно
при сильных нелинейных искажениях. Так при
разница
между точным значением ОСП и нижней границей составляет не более 0,5 дБ.
Однако при меньших значениях
N
целесообразнее воспользоваться точными
выражениями (19) или (20). Влияние знака
a3 на ОСП особенно заметно
при сильных нелинейных искажениях. Так при
![]() дБ
разница между значениями ОСП для случаев
дБ
разница между значениями ОСП для случаев
![]() и
и
![]() составляет
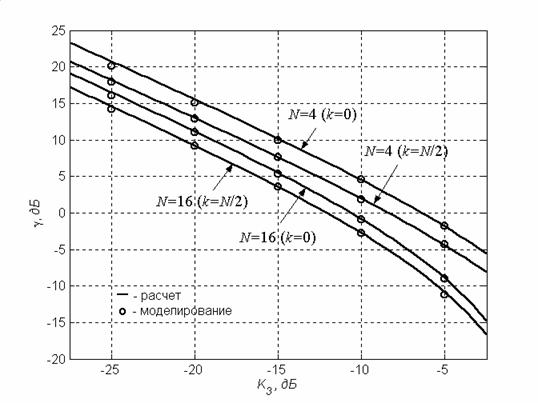
3…5 дБ. На рис. 4 сопоставлены результаты, полученные моделированием и
рассчитанные по точным формулам (19)-(20)
для случая
составляет
3…5 дБ. На рис. 4 сопоставлены результаты, полученные моделированием и
рассчитанные по точным формулам (19)-(20)
для случая
![]() .
Отметим тот факт, что разница в отношении сигнал/помеха для поднесущих,
находящихся в середине и на границах полосы ММН-сигнала, слабо зависит от
K3
и составляет приблизительно
.
Отметим тот факт, что разница в отношении сигнал/помеха для поднесущих,
находящихся в середине и на границах полосы ММН-сигнала, слабо зависит от
K3
и составляет приблизительно
![]() дБ.
дБ.
Рис. 3. Зависимость отношения сигнал/помеха от КНИ третьего порядка
Рис. 4.
Зависимость отношения сигнал/помеха от КНИ третьего порядка
(теоретический расчет и результаты моделирования)
Выражения (19)-(21) могут служить базой для оценки помехоустойчивости ММН-модемов при гладких нелинейных искажениях в высокочастотных каскадах аппаратуры связи. Однако для расчета вероятности ошибки необходимо знать также распределение квадратурных составляющих колебания помехи.
4. Распределение квадратурных составляющих помехи
Результаты анализа, проведенного в предыдущем
разделе, могут быть использованы для нахождения плотностей распределения
квадратурных составляющих помехи. Как было показано, помеховое колебание
представляет собой сумму
![]() синусоидальных
колебаний с амплитудами
синусоидальных
колебаний с амплитудами
![]() ,
и
,
и
![]() синусоидальных
колебаний с удвоенными амплитудами
синусоидальных
колебаний с удвоенными амплитудами
![]() .
Квадратурным составляющим синусоидального колебания с фиксированной амплитудой
.
Квадратурным составляющим синусоидального колебания с фиксированной амплитудой
![]() и
случайной фазой, равномерно распределенной в интервале
и
случайной фазой, равномерно распределенной в интервале
![]() ,
соответствует характеристическая функция вида [7]
,
соответствует характеристическая функция вида [7]
где
![]() –
функция Бесселя первого рода нулевого порядка. Тогда характеристическая
функция суммарного колебания помехи на
k-й поднесущей будет иметь вид
–
функция Бесселя первого рода нулевого порядка. Тогда характеристическая
функция суммарного колебания помехи на
k-й поднесущей будет иметь вид
Подставляя в (23) выражения
для
![]() получим
получим
Плотность распределения квадратурных составляющих помехового колебания находится по характеристической функции (24) с помощью обратного преобразования Фурье [7]. К сожалению, результат обратного преобразования Фурье от (24) не выражается через элементарные функции. Ряд полезных аппроксимаций можно получить, воспользовавшись разложением функции Бесселя в степенной ряд с ограниченным числом членов. Например, оставляя в разложении функции Бесселя один член, получим нормальную аппроксимацию плотности распределения. Однако очевидно, что такая аппроксимация справедлива только при больших N.
Другой подход, приводящий к полезным аналитическим результатам, заключается в вычислении моментов (или связанных с ними величин) по известной характеристической функции (24). В частности, универсальной характеристикой случайной величины являются кумулянты, которые можно найти дифференцированием логарифма характеристической функции [7]
Так как распределение (24)
симметрично, все кумулянты, соответствующие нечетными индексам
t,
будут равны нулю. Кумулянты с четными индексами могут быть вычислены
аналитически. Полагая, что
![]() ,
получим для первых трех четных индексов (
,
получим для первых трех четных индексов (![]() ):
):
где
![]() ,
,
![]() .
Кумулянты, вычисленные согласно (26), можно использовать
для оценки сходимости распределения (24) к нормальному
закону. В частности, характеристикой сходимости распределения (24)
к нормальному закону может служить коэффициент эксцесса
.
Кумулянты, вычисленные согласно (26), можно использовать
для оценки сходимости распределения (24) к нормальному
закону. В частности, характеристикой сходимости распределения (24)
к нормальному закону может служить коэффициент эксцесса
![]() ,
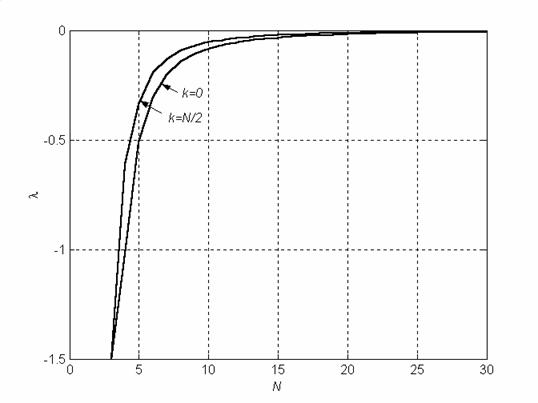
зависимость которого от количества поднесущих сигнала ММН показана на
рис.5.
,
зависимость которого от количества поднесущих сигнала ММН показана на
рис.5.
Рис. 5. Зависимость коэффициента
эксцесса распределения (24)
от количества поднесущих сигнала ММН
Из графиков на рис. 5 видно,
что коэффициент эксцесса
![]() довольно
быстро увеличивается с ростом N, асимптотически приближаясь к нулю. В то же
время, при
довольно
быстро увеличивается с ростом N, асимптотически приближаясь к нулю. В то же
время, при
![]() значение
значение
![]() увеличивается
относительно медленно. Например, при
увеличивается
относительно медленно. Например, при
![]() значения
коэффициента эксцесса составляют
значения
коэффициента эксцесса составляют
![]() (для
центральной поднесущей) и
(для
центральной поднесущей) и
![]() (для
крайних поднесущих ММН-сигнала), а при
(для
крайних поднесущих ММН-сигнала), а при
![]() эти
значения равны
эти
значения равны
![]() и
и
![]() соответственно.
соответственно.
Очевидно, что при большом числе поднесущих сигнала ММН (![]() )
использование нормальной аппроксимации распределения квадратурных составляющих
помехи является допустимым. С другой стороны, нормальная аппроксимация
распределения (24) не может быть оправдана при
)
использование нормальной аппроксимации распределения квадратурных составляющих
помехи является допустимым. С другой стороны, нормальная аппроксимация
распределения (24) не может быть оправдана при
![]() .
Значения
.
Значения
![]() соответствуют
в определенном смысле переходной области, в которой нормальная аппроксимация
приемлема при больших и умеренных вероятностях ошибки, но, в то же время,
может привести к некорректным результатам при слабых нелинейных искажениях,
когда вероятность ошибки мала.
соответствуют
в определенном смысле переходной области, в которой нормальная аппроксимация
приемлема при больших и умеренных вероятностях ошибки, но, в то же время,
может привести к некорректным результатам при слабых нелинейных искажениях,
когда вероятность ошибки мала.
5. Результаты моделирования
Для оценки адекватности гауссовской модели помех было проведено имитационное
моделирование. Исследование проводилось для двух модемов с 4-позиционной
относительно-фазовой манипуляцией (ОФМ) с числом поднесущих
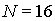 и
и
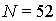 соответственно.
Вероятность ошибки на бит для 4-позиционной ОФМ при нормальной аппроксимации
квадратурных составляющих помехи может быть найдена по точным формулам
[1]:
соответственно.
Вероятность ошибки на бит для 4-позиционной ОФМ при нормальной аппроксимации
квадратурных составляющих помехи может быть найдена по точным формулам
[1]:
где
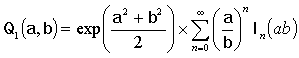 ,
,
![]() –
модифицированная функция Бесселя
n-го
порядка первого рода, а параметры
a
и
b
определяются через отношение сигнал/помеха:
–
модифицированная функция Бесселя
n-го
порядка первого рода, а параметры
a
и
b
определяются через отношение сигнал/помеха:
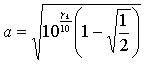 ,
,
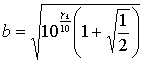 .
.
Результаты теоретических расчетов и имитационного моделирования приведены на
рис.6 и рис.7. При расчетах и
моделировании средняя вероятность ошибки (![]() )
находилась путем усреднения по всем поднесущим сигнала ММН. На рисунках также
показаны вероятности ошибки для поднесущих, расположенных в середине и на
границах диапазона, полученные расчетным путем. Все графики соответствуют
случаю
)
находилась путем усреднения по всем поднесущим сигнала ММН. На рисунках также
показаны вероятности ошибки для поднесущих, расположенных в середине и на
границах диапазона, полученные расчетным путем. Все графики соответствуют
случаю
![]() .
.
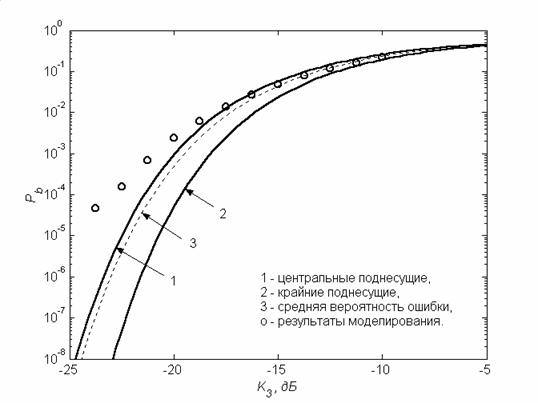
Рис. 6. Зависимость вероятности ошибки на бит от КНИ третьего порядка при N=16.
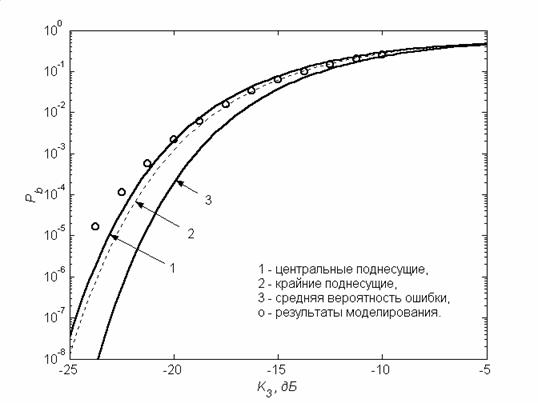
Рис. 7. Зависимость вероятности ошибки на бит от КНИ третьего порядка при N=52.
Как показал анализ, при
![]() нормальная
аппроксимация распределения квадратурных составляющих помехи приводит к
существенно заниженным результатам уже при вероятностях ошибки
нормальная
аппроксимация распределения квадратурных составляющих помехи приводит к
существенно заниженным результатам уже при вероятностях ошибки
![]() .
Для сигнала с
.
Для сигнала с
![]() такое
расхождение наблюдается при
такое
расхождение наблюдается при
![]() .
При этом пороговый эффект, обусловленный усеченностью распределения помех,
проявляется при гораздо меньших вероятностях ошибки. Указанное обстоятельство
ограничивает область применения гауссовской модели помех теми случаями, когда
количество поднесущих сигнала ММН исчисляется сотнями или тысячами. При малом
числе поднесущих (
.
При этом пороговый эффект, обусловленный усеченностью распределения помех,
проявляется при гораздо меньших вероятностях ошибки. Указанное обстоятельство
ограничивает область применения гауссовской модели помех теми случаями, когда
количество поднесущих сигнала ММН исчисляется сотнями или тысячами. При малом
числе поднесущих (![]() )
гауссовская аппроксимация приводит к существенным расхождениям между
теоретическими и экспериментальными результатами.
)
гауссовская аппроксимация приводит к существенным расхождениям между
теоретическими и экспериментальными результатами.
В
работе проведен анализ помехоустойчивости модемов со многими несущими при
нелинейных искажениях в высокочастотных каскадах аппаратуры связи. Получены
точные аналитические выражения, позволяющие рассчитать эквивалентное отношение
сигнал/помеха для каждой поднесущей сигнала ММН при произвольном числе
поднесущих. Показано, что при малом числе поднесущих (![]() )
распределение квадратурных составляющих помехи носит существенно негауссов
характер.
)
распределение квадратурных составляющих помехи носит существенно негауссов
характер.
Полученные результаты позволяют сформулировать наиболее актуальные задачи для дальнейших исследований. На наш взгляд, к таким задачам следует отнести, во-первых, обобщение результатов работы на случай, когда нелинейные искажения третьего порядка не являются доминирующими, и, во-вторых, поиск простых аппроксимаций распределений квадратурных составляющих помех при малом числе поднесущих.
7. Литература
1. Прокис Дж. Цифровая связь. Пер. с англ. /под ред. Д.Д. Кловского. – М.: Радио и связь, 2000
2. Hirosaki B. An orthogonally multiplexed QAM system using the discrete Fourier transform //IEEE Transactions on Comm, vol. 29 (Jul.), 1981, pp. 982-989
3. Merchan S., Armada A. G., and Garcia J. OFDM Performance in Amplifier Nonlinearity //IEEE Transactions on Broadcasting, vol. 44, March, 1998, pp. 106-114
4. Costa E., Midrio M., Pupolin S. Impact of amplifier non-linearities on OFDM transmission system performance //IEEE Communications Letters, Vol. 3, no. 2 (Feb.), 1999
5. Bannelli P., Cacopardi S. Theoretical analysis and performance of OFDM signals in nonlinear AWGN channels //IEEE Transactions on Communications, Vol. 48, No. 3., 2000, pp. 430–441
6. Dardari D., Tralli V., Vaccari A. A theoretical characterization of nonlinear distortion effects in OFDM systems // IEEE Transactions on Communications, Vol. 48, No. 10., 2000, pp. 1755–1764
7. Левин Б.Р. Теоретические основы статистической радиотехники. т.2, М.: «Сов. Радио», 1975
8. Gill M.C., Cook S.C., Giles T.C. and Ball J.T. A 300 to 3600 bps Multi-Rate HF Parallel Tone Modem //Proceedings IEEE Conference on Military Communications (MILCOM ’95), San Diego USA, Vol 3, 1995, pp.1066-1070
9. Жидков С.В. Архитектура аппаратных средств и программного обеспечения устройства цифровой передачи речи для радиостанций КВ диапазона //Всероссийская научно-техническая дистанционная конференция «Электроника», – Москва, 2001, http://econf.allvuz.ru
10. Грибов Э.Б. Нелинейные явления в приемо-передающем тракте аппаратуры связи на транзисторах. М., «Связь», 1971
11. Радиопередающие устройства /В.В. Шахгильдян, В.Б. Козырев, А.А. Ляховкин и др.; под ред. В.В. Шахгильдяна. – М.: Радио и связь, 1996
12. ГОСТ 22579-86. Радиостанции с однополосной модуляцией сухопутной подвижной службы. Типы, основные параметры и методы измерений.
13. Акимов П.С., Ефремов В.С. Характеристики обнаружения рангового радиолокационного обнаружителя //Радиотехника и электроника, №7, т.19, 1974, стр. 1527-1537
|
|
|
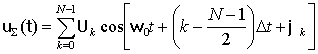 ,
,
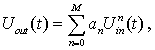 где
где
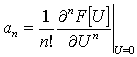 .
.
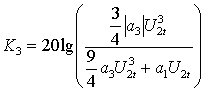
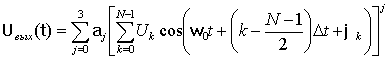 ,
,
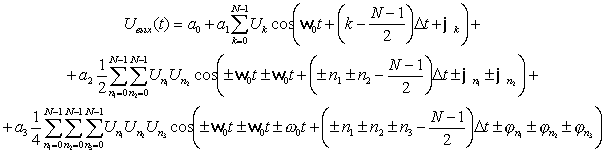 ,
(5)
,
(5)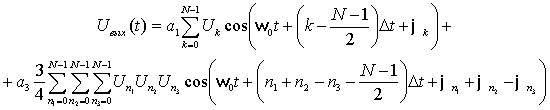 .
. (11)
(11)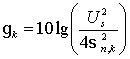
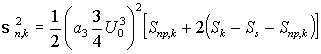 (15)
(15)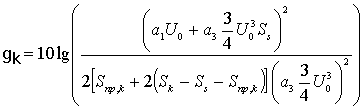
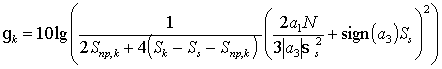
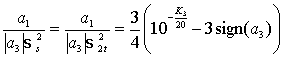 ,
(18)
,
(18)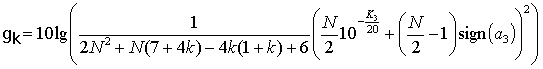
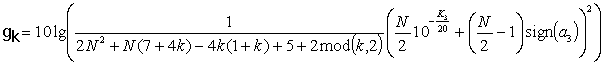
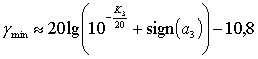
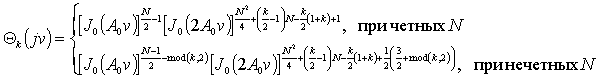 (24)
(24)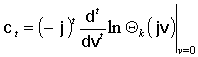 .
(25)
.
(25)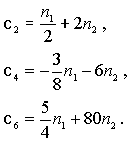 (26)
(26)