|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 2, 2004 |
|
ДВУМЕРНО - ЭКВИДИСТАНТНАЯ РЕШЕТКА ЩЕЛЕВЫХ ИЗЛУЧАТЕЛЕЙ, КОНЕЧНЫХ РАЗМЕРОВ ПО ОДНОЙ КООРДИНАТЕ И БЕСКОНЕЧНАЯ ПО ДРУГОЙ, СОДЕРЖАЩАЯ ДВЕ ЩЕЛИ НА ПЕРИОДЕ.
М.Д. Дупленкова
Московкий энергетический институт
Получена 16.02.2004 г.
Рассмотрена двумерно-эквидистантная решетка щелевых излучателей на основе плоского волновода, конечная вдоль оси 0x и бесконечная вдоль оси 0y, содержащая две щели на периоде. Анализ этой структуры, проводимый в рамках строгого подхода, связан с непосредственным решением электродинамической задачи для конечной решетки. На основе полученного решения построен эффективный численный алгоритм, позволяющий определять основные внешние характеристики рассматриваемой решетки: распределение токов на щелях, матрицу рассеяния, диаграмму направленности и коэффициент усиления. Представлены результаты численных расчетов. Показано, что антенная решетка, содержащая две щели на периоде, позволяет преодолеть один из основных недостатков антенн бегущей волны – невозможность излучения по нормали.
1. Введение
Работа посвящена методам анализа антенных решеток щелевых излучателей на основе плоского металлического волновода и является продолжением серии работ [1,2,3], посвященных антеннам данного типа. В работах [1,2] исследована бесконечная двумерно-периодическая решетка щелей. В работе [3] получено электродинамическое решение задачи о возбуждении решетки конечной длины, возбуждаемой собственной волной плоского волновода, падающей под произвольным углом. В данной работе мы продолжаем исследование антенных решеток такого типа, причем нас интересуют решетки, содержащие две щели на периоде, для которых предложено строгое электродинамическое решение задачи о возбуждении решетки собственной волной плоского волновода, падающей под произвольным углом. Поле в щелях описывается одной тригонометрической функцией, как и в работе [1].
2. Постановка задачи.
В данном разделе приводится электродинамическое решение задачи о возбуждении решетки, содержащей две разные щели на периоде, конечной по оси 0x. Щели повернуты относительно оси 0y на углы соответственно q1 и q2, и смещены относительно начала координат таким образом, что центры щелей имеют координаты соответственно x10, y10 и x20, y20. Исследуемая структура изображена на рис. 1. Будем полагать, что решетка бесконечна по оси 0y и возбуждается основной Т-волной плоского волновода высотой h между бесконечно тонкими идеально проводящими поверхностями. Волна распространяется под углом j к оси 0x.
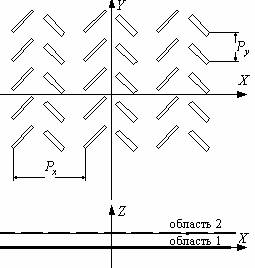
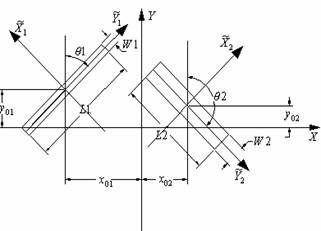
Рис.1
Считаем, что распределение поверхностного магнитного тока в эквивалентной
щели с электрическим полем Е0, определяемый формулой ![]() имеет только одну продольную
составляющую
имеет только одну продольную
составляющую ![]() или
или ![]() , что справедливо для достаточно
узких щелей.
, что справедливо для достаточно
узких щелей.
Полагаем также, что указанные компоненты магнитных токов в щелях, расположенных на нулевом периоде решетки, описываются следующими функциями:
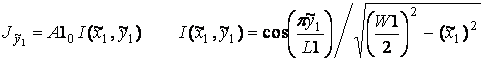 , (1)
, (1)
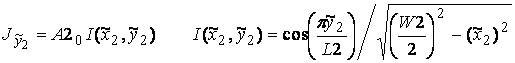 , (2)
, (2)
где А10, А20 – напряжения между кромками первой и второй щелей соответственно, имеет размерность Вольт, L1 - длина первой щели, W1 - ширина первой щели, L2 - длина второй щели, W2 - ширина второй щели. Токи в щелях описываются одной базисной функцией, так как гармоники высших порядков слабо влияют на форму диаграммы направленности и на коэффициент отражения, что было показано в работе [2].
В других щелях магнитный ток отличается от магнитного тока в начале координат только амплитудными множителями. Присвоим всем периодам решетки, содержащим две щели, номера, характеризующие их положение относительно начала координат. Номер n соответствует координате у и меняется от -¥ до ¥. Нулевой номер имеет период расположенный в начале координат. Номер m меняется от 0 до M-1, где M- число периодов в решетке по координате x. На периодах с номерами m¹0 магнитные токи отличаются от токов на периоде с m=n=0 (1,2) только амплитудными множителями Аm, которые необходимо определить. Пусть поле падающей волны зависит от х, у следующим образом:
![]() , (3)
, (3)
где - b0 и kt – проекции волнового вектора волны на оси 0y и 0x. Параметр b0 в силу бесконечности решетки вдоль оси 0y задает зависимость комплексных амплитуд полей в щелях. С учетом этой зависимости можно записать выражение для магнитных токов на n,m – ом периоде:
![]() , (4)
, (4)
![]() .
.
Множители А1m, А2m определяются из системы линейных алгебраических уравнений (СЛАУ), которая возникает из системы интегральных уравнений для магнитных токов. Из выражения (4) в частности следует, что магнитные токи на щелях будут полностью определены, если будут найдены коэффициенты А1m, А2m.
3. Вывод системы интегральных уравнений
Система интегральных уравнений (СИУ) и далее СЛАУ выводятся из решения граничной задачи. Процедура вывода СИУ для решетки, конечной по оси 0х аналогична случаю бесконечной решетки и достаточно подробно была изложена в работах [1,2]. Поэтому приведем здесь лишь схему решения граничной задачи. Нам необходимо найти решение уравнений Максвелла в областях 1 и 2, удовлетворяющее следующим граничным условиям (ГУ) [4]:
Еt1,2=0 при z=-h -¥<x,y<¥ (5)
Еt1,2=0 при z=0 -¥<x,y<¥, кроме x,yÎSщ (6)
Еt1 =Еt2 в области щелей (7)
Нt1= Нt2 в области щелей (8)
Решение граничной задачи предусматривает следующие шаги:
1) Щель в экране заменяем двумя листками поверхностного магнитного тока [5], расположенными по обе стороны полностью металлизированного экрана. Таким образом, одна щель эквивалентна двум противоположно направленным листкам магнитного тока, расположенным в областях 1 и 2 на полностью металлизированном экране. Благодаря этому обстоятельству сразу выполняется ГУ (7).
2) Находим поле, создаваемое поверхностными магнитными токами в областях 1,2. Это поле удовлетворяет всем ГУ, кроме (8).
3) Выражаем Нt1 и Нt2 через (1,2) и приравниваем их в соответствии с (8). В силу периодичности поля по координате у достаточно обеспечить непрерывность магнитного поля в одной линейке щелей, например с номером n=0. Для линеек щелей с разными номерами m необходимо обеспечить выполнение граничных условий индивидуально. В результате удовлетворения граничных условий для магнитного поля получается следующую систему равенств:
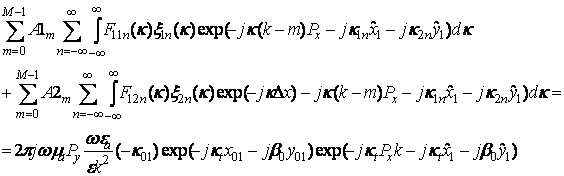 (9)
(9)
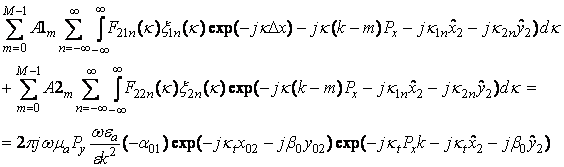 (10)
(10)
где ![]()
k1 и k0 волновые
числа среды, заполняющей плоский волновод и свободного пространства, ![]()
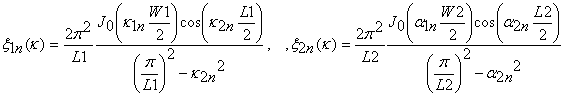
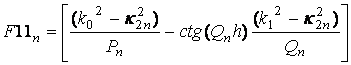 (11)
(11)
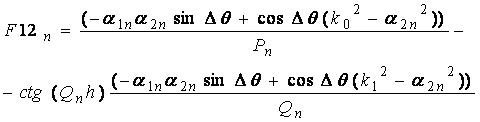
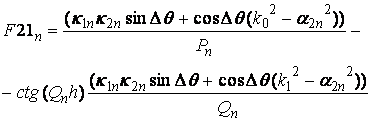
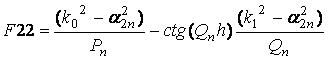
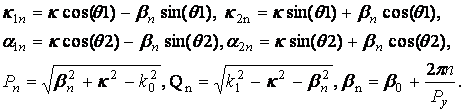
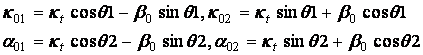
В (15), (16) индекс k
пробегает те же значения, что и индекс m, а
переменные ![]() меняются
в пределах областей, совпадающих с областями, занятыми щелями на периоде с
индексами n=m=0.
Выражения (15), (16) можно привести к системе линейных алгебраических уравнений
относительно неизвестных Аm с
помощью процедуры Галеркина [5]. Для этого каждое равенство из системы (9)
умножаем на функцию (1) и интегрируем равенство по всей области определения
(9), а каждое равенство из системы (10) умножаем на функцию (2) и интегрируем
равенство по всей области определения (10). В результате интегрирования
получаем следующую систему линейных алгебраических уравнений:
меняются
в пределах областей, совпадающих с областями, занятыми щелями на периоде с
индексами n=m=0.
Выражения (15), (16) можно привести к системе линейных алгебраических уравнений
относительно неизвестных Аm с
помощью процедуры Галеркина [5]. Для этого каждое равенство из системы (9)
умножаем на функцию (1) и интегрируем равенство по всей области определения
(9), а каждое равенство из системы (10) умножаем на функцию (2) и интегрируем
равенство по всей области определения (10). В результате интегрирования
получаем следующую систему линейных алгебраических уравнений:
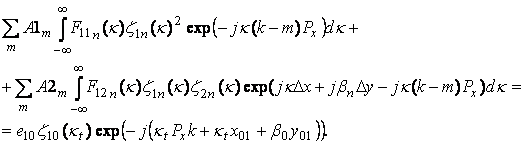 (12)
(12)
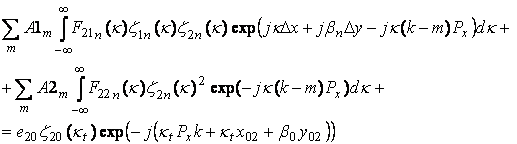 (13)
(13)
где
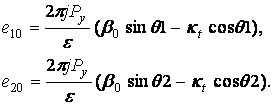
Введем следующие обозначения:
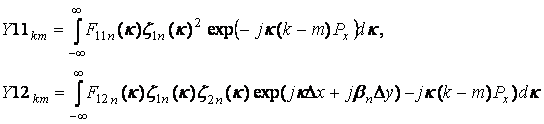
![]() (14)
(14)
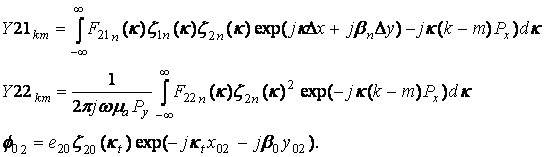 (15)
(15)
С учетом (14), (15) система (12)-(13) приобретает новый вид:
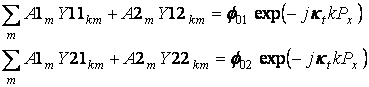 (16)
(16)
Таким образом, нам удалось привести исходную электродинамическую задачу к системе линейных алгебраических уравнений (СЛАУ), размерность которой меняется в зависимости от количества элементов рассматриваемой решетки.
Величины Y11km, Y12km, Y21km, Y22km имеют простой физический смысл. Можно рассматривать конечную по оси 0x и бесконечную по оси 0y решетку как M бесконечных пар линеек щелей. В этом случае величинам Ykm можно приписать смысл взаимных проводимостей линеек щелей, которые описывают взаимодействие k-ого периода с m-ым. Например, величина Y11km описывает взаимодействие первой щели на k-ом периоде с первой щелью на m-ом периоде; Y12km - описывает взаимодействие первой щели на k-ом периоде со второй щелью на m-ом периоде и т.д.
4. Алгоритм вычисления коэффициентов СЛАУ
Численное решение (16) представляет определенную сложность из-за того, что при расчете Ykm интегрирование в бесконечных пределах нерегулярной функции, а затем двойное суммирование требуют больших ресурсов ЭВМ. Построению эффективных алгоритмов численного решения задач подобного типа посвящены раздел 2 работы [2] и раздел 3 работы [3]. Повторяем рассуждения, изложенные в этих работах, и опуская громоздкие промежуточные выкладки, приводим лишь конечные результаты вычисления коэффициентов СЛАУ для решетки, имеющей две щели на периоде.
Используя преобразование Пуассона [6] представим равенства (14), (15) в следующем виде:
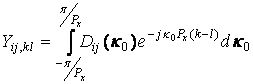 , (17)
, (17)
где индексы i,j=1,2,
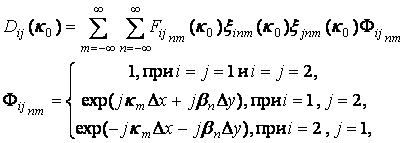
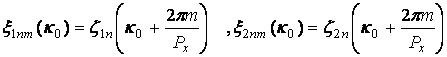 (18)
(18)
где функции ![]() определяются в соответствии с
(11), однако нужно сделать замену:
определяются в соответствии с
(11), однако нужно сделать замену: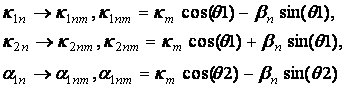
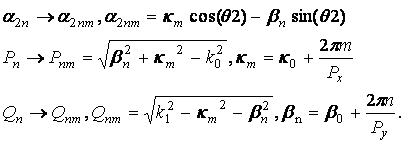 (19)
(19)
Особенностью (17) является то, что интегрирование ведется уже в конечных пределах, а подынтегральные функции, главными частями которых являются функции Dij(k) хорошо изучены ранее в работе [2].
Для построения эффективных алгоритмов вычисления функций Dij(k) представляем их как сумму регулярной и нерегулярной частей:
![]() , (20)
, (20)
где индексы i,j=1,2, SSij(k) – описывают особенности типа простых полюсов функций Dij(k):
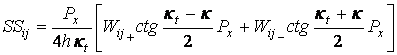 , (21)
, (21)
где
![]() , (22)
, (22)
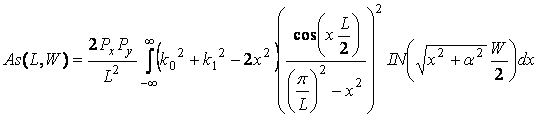
ААij(k) – описывают особенности типа точек ветвления функций Dij(k):
 (23)
(23)
где 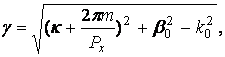 а d=const, выбирается так, чтобы ряд по m был быстро сходящимся,
а d=const, выбирается так, чтобы ряд по m был быстро сходящимся, ![]() определяем из условия
определяем из условия
![]() (24)
(24)
где ![]() .
.
Qij(k) - описывают регулярные части функций Dij(k):
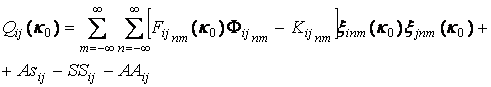
![]() (25)
(25)

 ,
,
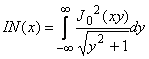 , функции SSij определены выражением (21), а
функции ААij определены выражением (23).
, функции SSij определены выражением (21), а
функции ААij определены выражением (23).
В соответствии с выражением (17) проинтегрируем функции (20) на отрезке от -p/Px до p/Px. В результате получаем следующие выражения для коэффициентов СЛАУ (16):
![]()
![]() , (26)
, (26)
где
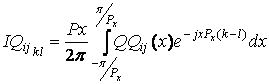 . (27)
. (27)
Функции Qij(k) - гладкие, поэтому численное интегрирование не представляет сложности. Эти функции определяются выражением (25).
Функции SSij(k) определяются выражениями (21) - (22). Интегралы от них вычисляем аналитически:
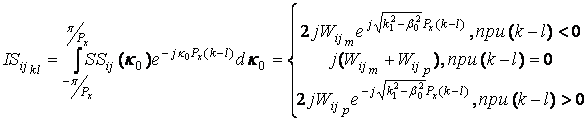
(28)
где ![]() определяются
выражением (22).
определяются
выражением (22).
Функции ААij(k) определяются выражениями (23) - (24). Интегралы от них также вычисляем аналитически:
 (29)
(29)
где ![]() и
и
![]()
![]() определяются
выражением (24),
определяются
выражением (24), ![]() -
функция Ханкеля второго рода нулевого индекса,
-
функция Ханкеля второго рода нулевого индекса, ![]() - функция Ханкеля второго рода первого
индекса.
- функция Ханкеля второго рода первого
индекса.
Таким образом, коэффициенты СЛАУ (16), а значит и токи в щелях определены.
4. Матрица рассеяния
Рассчитаем одну из основных внешних характеристик, необходимых для проектирования антенных решеток с последовательным питанием: матрицу рассеяния. В соответствии с принципом суперпозиции элементы матрицы рассеяния решетки, содержащей две щели на периоде определяются следующим образом:
 при х=0, (30)
при х=0, (30) 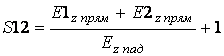 при
х=0, (31)
при
х=0, (31)
где E1,2z обр - Ez-компоненты отраженной волны, создаваемой только щелями соответственно первого и второго типа; E1,2z прям - Ez-компонента прошедшей волны, создаваемая только щелями соответственно первого и второго типа,
![]() . (32)
. (32)
В работе [3] было показано, что
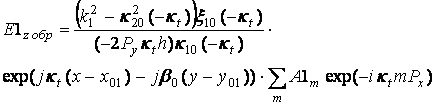 (33)
(33)
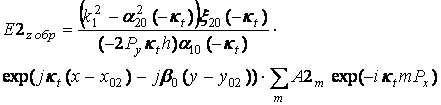 (34)
(34)
где ![]() ,
,![]() определяются выражениями (18), (19), А1,2m –амплитуды токов на щелях
соответственно первого и второго типа, определяемые в результате решения СЛАУ
(16).
определяются выражениями (18), (19), А1,2m –амплитуды токов на щелях
соответственно первого и второго типа, определяемые в результате решения СЛАУ
(16).
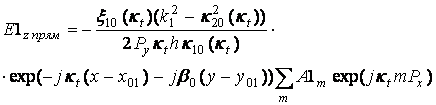 (35)
(35)
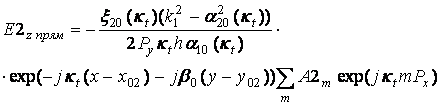 (36)
(36)
Подставляя (32)-(36) в (30), (31) получаем окончательные выражения для коэффициентов отражения и прохождения S11 и S12, которые имеют следующий вид:
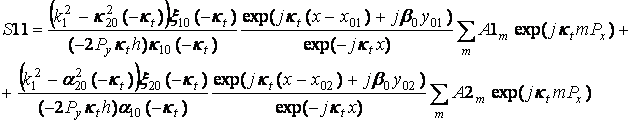 (37)
(37)
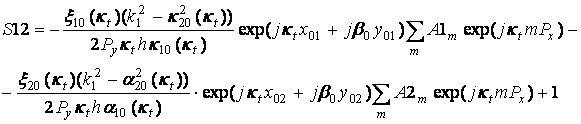 (38)
(38)
5. Диаграмма направленности и коэффициент усиления
Рассчитаем основные
внешние характеристиками антенной решетки: диаграмму направленности (ДН) и коэффициент
усиления (КУ). Для этого из решетки, имеющей M периодов по оси 0х и периодической по оси 0у,
делается вырезка из N
периодов по оси 0у. При этом полагаем, что распределение магнитных токов в
щелях решетки с конечным числом элементов по обоим координатам совпадает с
распределением магнитных токов, полученным для решетки, конечной в одном
направлении. Отметим также, что экран при z=0 полагается бесконечным. Таким образом, излучение
происходит только в верхнее полупространство. В дальнейшем нам будет удобно
пользоваться сферическими координатами ![]() . Введем их в соответствии с [4] (рис.2).
. Введем их в соответствии с [4] (рис.2).
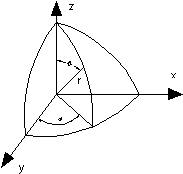
Рис.2
Получим выражение для векторного потенциала в дальней зоне для щели первого типа (параметры q1, W1, L1) и для щели второго типа (параметры q2, W2, L2), расположенных на нулевом периоде, воспользовавшись результатами, полученными в [3]:
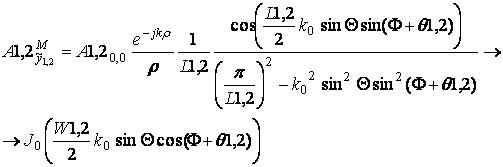 (39)
(39)
Определим теперь магнитный потенциал для полупространства, создаваемый всей совокупностью щелей первого типа и щелей второго типа. Используя (39) и принцип суперпозиции, получаем:
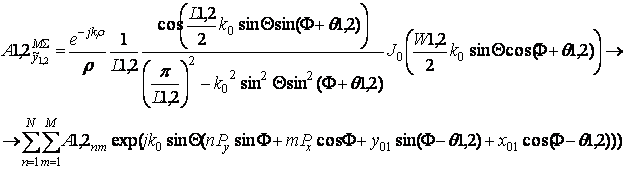 где
где ![]() . (40)
. (40)
Выразим теперь компоненты
напряженности электрического и магнитного полей через магнитные потенциалы.
Приведем, например выражение для ![]() -компоненты
поля, создаваемого магнитными токами в щелях первого типа:
-компоненты
поля, создаваемого магнитными токами в щелях первого типа:
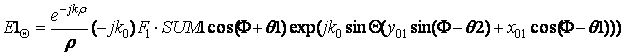 где мы обозначили
где мы обозначили ![]() - ДН одного элемента первого типа,
- ДН одного элемента первого типа,
![]() - множитель направленности решетки, состоящей только из
элементов первого типа.
- множитель направленности решетки, состоящей только из
элементов первого типа.
 ,(41)
,(41)
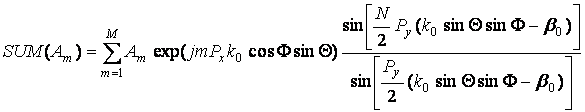 .(42)
.(42)
Аналогичным образом можно записать ![]() и т.д.
и т.д.
Определим компоненты напряженности электрического и магнитного поля, создаваемого всеми магнитными токами, пользуясь принципом суперпозиции:
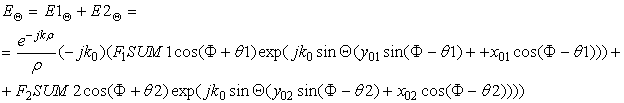 где
где ![]() ,
,![]() .
.
Аналогичным образом находим все остальные компоненты поля.
Запишем выражение для вектора Пойнтинга, который определяется следующим образом [4]:
![]() .
.
После несложных, но громоздких алгебраических преобразований, окончательно получаем:
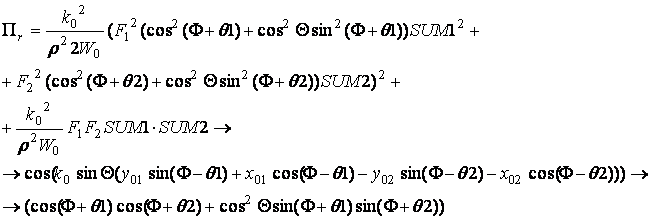 (43)
(43)
Нормированная ДН по мощности
определяется как: ![]() .
.
Получим выражение для коэффициента усиления решетки: повторяя рассуждения для вывода коэффициента усиления, получаем следующее выражение:
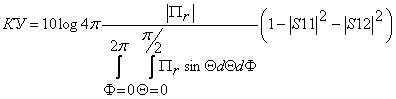 ,
,
где Пr определяется выражением (43), а S11, S12 – выражениями (37), (38).
6. Численные результаты
В этом разделе представлены некоторые результаты, полученные при численном анализе антенной решетки, имеющей две щели на периоде, бесконечной по оси 0y и конечной по оси 0x. Целью первого этапа численного исследования является проверка изложенной выше модели решетки с двумя щелями на периоде. Для этого одна и та же решетка моделируется как решетка с одной щелью и с двумя щелями на периоде. В идеальном случае обе модели должны давать одинаковые результаты. Результаты, представленные ниже получены для антенной решетки со следующими параметрами: h=4 мм, Py=10 мм, W=1 мм, e=2.25, f=0, AP=160 мм. При анализе использовались две математические модели:
математическая модель ММ1 - электродинамическое решение для решетки, содержащей одну щель на периоде, подробно изложенное в [3] (тогда Px=14 мм, число периодов на длине решетки N=12); на рисунках 3 – 7 этой математической модели соответствуют зависимости с номером 1;
математическая модель ММ2 - решение для решетки, содержащей две щели на периоде, изложенное в этой работе (тогда Px=28 мм, расстояние между 1-ой и 2-ой щелью равно 14 мм, число периодов на длине решетки N=6); на рисунках 3 –7 этой математической модели соответствуют зависимости с номером 2.
На рис. 3 приведен модуль амплитудного распределения токов на щелях на длине решетки. На рис.4 приведены частотные зависимости угла излучения решетки. На рис. 5 показаны частотные зависимости модулей коэффициентов отражения S11 и прохождения S21. На рис. 6 приведена нормированная диаграмма направленности в плоскости XOZ.
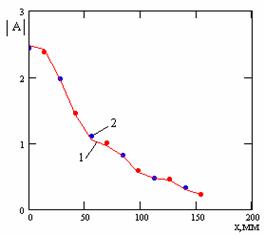
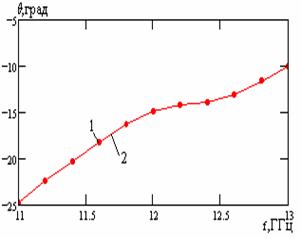
Рис.3 Рис.4
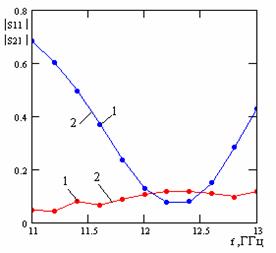
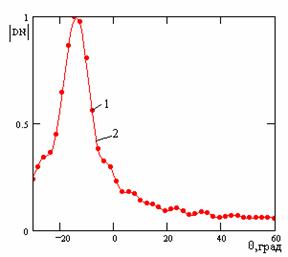
Рис.5 Рис.6
На рис 7 приведена частотная зависимость коэффициента усиления; для сравнения на графике приведена частотная зависимость коэффициента направленного действия антенны, имеющей такую же площадь, как и исследуемая антенна, и равномерное распределение токов на щелях, эта зависимость обозначена номером 3.
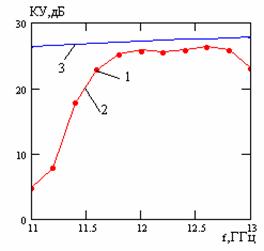
Рис. 7
Покажем, что антенная решетка, содержащая две щели на периоде, позволяет нам преодолеть один из основных недостатков антенн бегущей волны – невозможность излучения по нормали. Этот недостаток связан с так называемым эффектом нормали: отраженные волны от всех элементов складываются в фазе и поэтому коэффициент отражения от такой решетки очень велик. Для того, чтобы преодолеть этот недостаток, будем использовать решетку, содержащую две щели на периоде. Подбираем сначала взаимное расположение и геометрические размеры щелей на одном периоде таким образом, чтобы коэффициент отражения от такой линейки щелей стремился к нулю. Приводим далее полученные параметры: h=4 мм, L1=7.3 мм, W1=1 мм, L2=7 мм, W2=1 мм, e=2.25, x01= -2 мм, y01=2 мм, x02=0.9, y02=0 мм, q1=q2=33°, которые соответствуют зависимостям, приведенным на рис.8. Из рисунка видно, что коэффициент отражения от такой линейки щелей очень мал (S11<0.1),то есть щели согласованы, а коэффициент прохождения достаточно велик (S12>0.85).
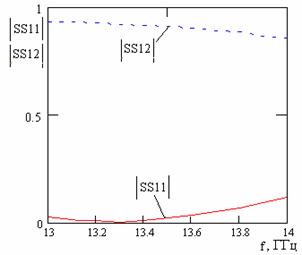
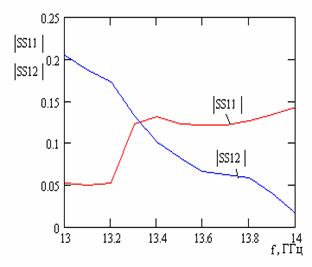
Рис.8 Рис.9
Затем переходим к решетке, состоящей из N=40 исследованных линеек, и добиваемся того, что коэффициент прохождения также становится мал (S12<0,2), что соответствует зависимостям, приведенным на рис.9. На рис. 10 приведена частотная зависимость коэффициента усиления, из которой хорошо видно, что данная решетка излучает по нормали на частоте f=13.28 ГГц. На рисунках 11 и 12 приведены соответственно диаграмма направленности в плоскости XOZ на частоте f=13.3 ГГц и частотная зависимость коэффициента усиления решетки. Для сравнения на рис.12, обозначенная цифрой 2, приведена частотная зависимость коэффициента направленного действия антенны, имеющей такую же площадь, как и исследуемая антенна, и равномерное распределение токов на щелях.
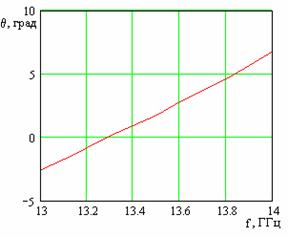
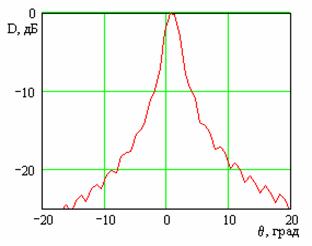
Рис.10 Рис.11
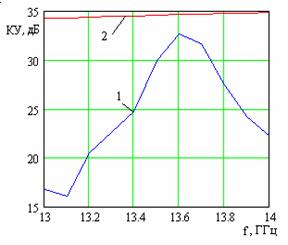
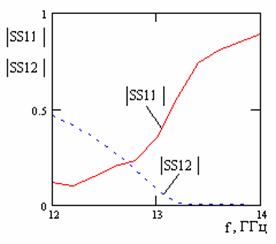
Рис.12 Рис.13
Чтобы продемонстрировать преимущества использования в данном случае решетку, содержащую две щели на периоде перед решеткой, содержащей одну щель на периоде, на рис. 13 приводим частотные зависимости коэффициентов отражения и прохождения для решетки имеющей такие же параметры, но длина второй щели стремится к нулю.
Таким образом, в данном разделе были приведены некоторые результаты численного исследования решетки, содержащей две щели на периоде, и показано, что такая решетка может излучать по нормали к плоскости решетки.
СПИСОК ЛИТЕРАТУРЫ.
1. Банков С.Е.// РЭ. 2001. т. 46. № 4.с.441
2. Банков С.Е, Дупленкова М.Д.// РЭ.2003. №3.
3. Банков С.Е, Бодров В.В, Дупленкова М.Д.//РЭ 2003. №6.
4. Марков Г.Т, Чаплин А.Ф. Возбуждение электромагнитных волн. М.:-Л., Энергия, 1967.
5. Бодров В.В, Сурков В.И. Математическое моделирование устройств СВЧ и антенн. М.: Изд-во МЭИ, 1994.
6. Владимиров В.С. Уравнения математической физики. М., Наука, 1988