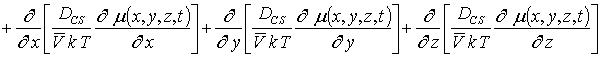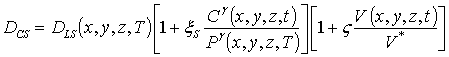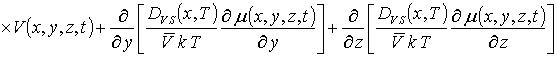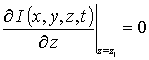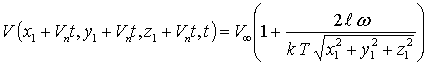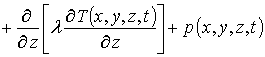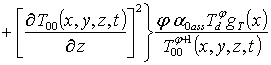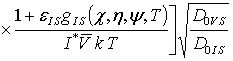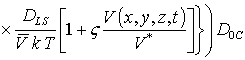Применение пористых слоев и оптимизация отжига примеси для увеличения резкости p-n-переходов в биполярных гетеротранзисторах

Е. Л. Панкратов

Нижегородский архитектурно-строительный университет
 

Получена 14 февраля 2011 г.
 

 

Аннотация. В данной работе рассматривается способ уменьшения глубины залегания биполярного транзистора в полупроводниковой гетероструктуре, а также увеличения равномерности распределения примеси в легированной области. Данный метод базируется на использовании многослойности гетероструктуры и оптимизации отжига. Для усиления обоих эффектов используется дефектность (пористость) одного из слоев гетероструктуры.

Ключевые слова: увеличение резкости p-n-переходов; оптимизация отжига; биполярные гетеротранзисторы; гетероструктуры с пористыми слоями.

Abstract. In this paper we consider an approach to decrease depth of p-n-junctions in a bipolar transistor in a semiconductor heterostructure. At one time with the decreasing of the depth homogeneity of dopant distributions in doped area increases. The approach based on application of inhomogeneity of the heterostructure and optimization of annealing time. To increase the both effects (decreasing of the depth and increasing of homogeneity of dopant distributions) it could be used inhomogenous distribution of defects (for example, porous) of materials of the heterostructure of materials.

Keywords: increasing of sharpness of p-n-junctions; optimization of annealing; bipolar heterotransistors; heterostructures with porous layers.

 

Введение

Одной из наиболее интенсивно решаемых проблем при проектировании интегральных схем (ИС) является уменьшение времени переключения входящих в их состав p-n-переходов (в том числе входящих в состав транзисторов и тиристоров), а также уменьшение глубины их залегания [1-3]. Одними из основных способов формирования p-n-переходов и биполярных транзисторов являются диффузия и ионная имплантация, а также эпитаксиальный рост [1-7]. Для уменьшения глубины залегания p-n-переходов могут быть использованы неоднородность температурного поля, сформированная приповерхностным (лазерным или микроволновым) отжигам [8,9]. Неоднородность распределения дефектов легируемой структуры также влияет на распределение примеси (см., например, [10-12] и соответствующие работы данных авторов). В работах [13-16] рассмотрен альтернативный способ уменьшения глубины залегания диффузионных и имплантационных p-n-переходов путем увеличения их резкости, базирующийся на их формировании в окрестности границы раздела между слоями двухслойной гетероструктуры (Г). Одновременно с уменьшением глубины залегания p-n-переходов происходит увеличение равномерности распределения примеси в легированной области Г по сравнению с аналогичным распределением примеси в однородном материале [13-16]. Первый эффект приводит к уменьшению времени прохождения носителей заряда через p-n-переход. Второй эффект приводит к уменьшению локального разогрева материала в легированной области. Оба эффекта могут быть усилены применением микроволнового или лазерного отжига [15,16]. 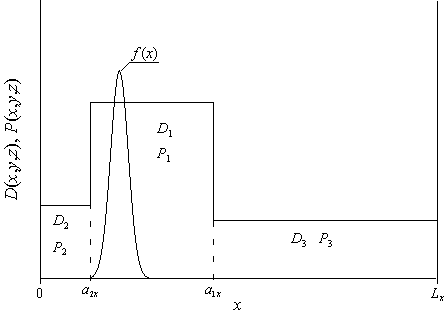В данной работе рассматривается трехслойная Г, состоящая из подложки (П) и двух эпитаксиальных слоев (ЭС) (см. рис. 1). Ближний к П эпитаксиальный слой обозначим как ЭС₁ и будем считать его пористым, что способствует увеличению равномерности распределения примеси [17]. Второй ЭС обозначим как ЭС₂. Будем считать, что тип проводимости П и ЭС₂ одинаковы (p или n). В ЭС₁ имплантируется примесь для формирования в данном слое второго типа проводимости (n или p). Далее проводится микроволновый отжиг радиационных дефектов. В течении отжига распределение примеси уширяется. Энергию ионов и толщину ЭС₁ целесообразно подобрать таким образом, чтобы к окончанию отжига примесь достигла бы границ раздела между слоями рассматриваемой Г. Если примесь не достигла границ раздела, целесообразно провести дополнительный отжиг примеси. Для усиления обоих эффектов (и резкости p-n-переходов, и равномерности распределения примеси) целесообразно использовать микроволновый отжиг из-за неоднородности температурного поля. Основной целью данной работы является оптимизация длительности отжига в требуемой области параметров с учетом трансформации пористости и развитие методики анализа массо- и теплопереноса позволяющего провести требуемую оптимизацию.
 

Рис. 1. Зависимость коэффициента диффузии D(x,y,z) и растворимости P(x,y,z) примеси от координаты x в трехслойной гетероструктуре. В направлениях, перпендикулярных оси Ox, гетероструктура имеет размеры yÎ[0,L_y] и zÎ[0,L_z]. В среднем слое приведено начальное (до отжига) распределение примеси f (x).

 

Методика анализа

Перераспределение примеси в рассматриваемой гетероструктуре определим путем решения следующего уравнения [1-3]

 (1)

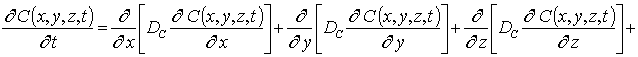
с граничными и начальным условиями

, , , ,

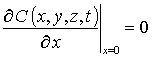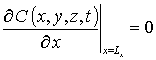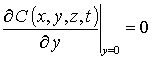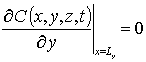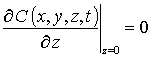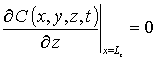, , C (x,y,z,0)=f_C  (x,y,z).                     (2)

В соотношениях (1) и (2) введены следующие обозначения: C(x,y,z,t) – пространственно-временное распределение концентрации примеси, k – постоянная Больцмана, T – температура отжига, m (x,y,z,t) – химический потенциал,  - молярный объем, D_С и D_СS  – коэффициенты объемной и поверхностной диффузии примеси. Величина коэффициента диффузии определяется свойствами материалов в слоях Г, скорости прогрева и охлаждения Г (в соответствии с законов Аррениуса), а также пространственно-временными распределениями концентраций примесей и радиационных дефектов. Последние две зависимости коэффициента диффузии могут быть аппроксимированы следующим соотношением [2,11]

.               (3)

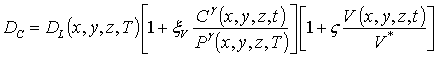
В данном соотношении D_L (x,y,z,T) и D_LS (x,y,z,T) – пространственные (за счет многослойности Г) и температурные (по закону Аррениуса) зависимости коэффициентов диффузии; P (x,y,z,T) – предел растворимости примеси; определяемый свойствами материала параметр g может принимать целые значения в интервале g Î[1,3] [2]; V (x,y,z,t) - пространственно-временное распределение концентрации радиационных вакансий; V^* - равновесное распределение вакансий. Концентрационная зависимость коэффициентов диффузии подробно обсуждается в [2]. Пространственно-временное распределение радиационных дефектов определялось с помощью следующей системы уравнений [18,19]

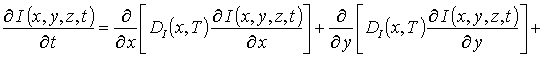
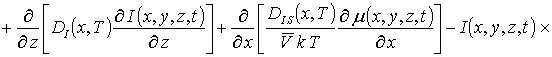     (4)

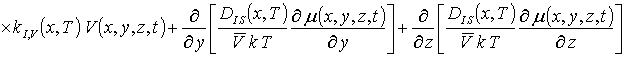
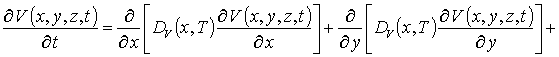
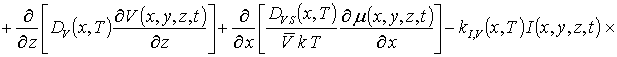
с начальными

r (x,y,z,0)=f_r  (x,y,z)                                                     (5а)

и граничными условиями

, , , ,

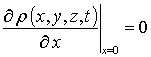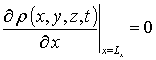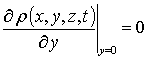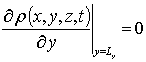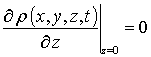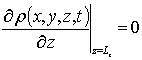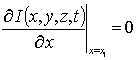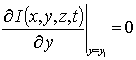, , ,  (5б)

, .

В системе уравнений (4) r =I,V; I (x,y,z,t) – пространственно-временное распределение концентрации междоузельных атомов; D_r(x,y,z,T) – коэффициенты диффузии междоузельных атомов и вакансий; k_I,V(x,y,z,T) – параметр рекомбинации дефектов; k – постоянная Больцмана; V_¥ - равновесная концентрация вакансий; w  = a³, a – межатомное расстояние;  - удельная поверхностная энергия. При учете пористости ЭС₁ считалось, что перед началом отжига поры имеют практически цилиндрическую форму со средними размерами  и z₁ [12]. С течением времени мелкие поры распадаются на вакансии, которые поглощаются более крупными порами [20]. Более крупные поры, увеличиваясь за счет вакансий от более мелких пор, постепенно принимают все более шарообразную форму [20]. Распределение концентрации вакансий в Г, возникающее за счет пористости, может быть определено суммированием по всем порам, т.е.

, .

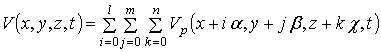В данном соотношении введены обозначения: a, b и c - средние расстояния между центрами пор в направлениях x, y и z; l, m и n – количество пор в соответствующих направлениях.

Пространственно-временное распределение температурного поля при микроволновом отжиге описывалось с помощью второго закона Фурье [21]

                                          (6)

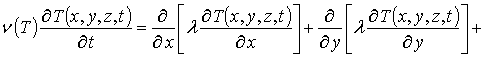
с граничными и начальным условиями

, , , , , ,

T (x,y,z,0)=f_T  (x,y,z),                     (7)

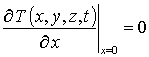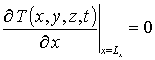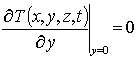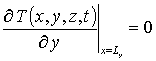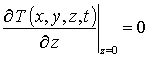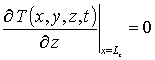где T(x,y,z,t) – пространственно-временное распределение температуры; n (T)= n_ass[1-h exp(-T(x, y,z,t)/T_d)] – теплоемкость материала (в представляющем наибольший интерес случае, когда температура сопоставима по величине с температурой Дебая или превышает ее, можно считать, что n (T)»n_ass); T_d – температура Дебая [21]; l – коэффициент теплопроводности, величина которого определяется свойствами материалов Г и температурой; температурная зависимость коэффициента теплопроводности в представляющей наибольший интерес области температур может быть аппроксимирована следующим образом: l(x,y,z,T)=l_ass(x) [1+m (T_d/T(x,y,z,t) )^j] (см., например, [21]); p(x,y,z,t) – выделяющаяся в Г объемная плотность мощности; a(x,y,z, T)=l(x,y,z,T)/n (T) – коэффициент температуропроводности.

На первом этапе определим пространственно-временное распределение температурного поля. Для этого следуя [13,14] представим независимый от температуры множитель коэффициента температуропроводности в виде суммы постоянной и переменной составляющих: a _ass (x)=a_0ass[1+e_T g_T(x)]. Далее будем искать решение уравнения (6) в виде следующего степенного ряда

.                                  (8)

Подстановка данного ряда в уравнение (6) позволяет получить систему уравнений для исходного приближения температуры T₀₀(x,y,z,t), а также поправочных функций к нему T_ij(x,y,z,t) (i³1, j³1) в следующей форме

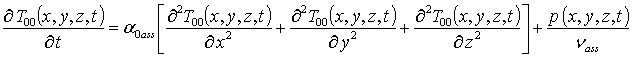
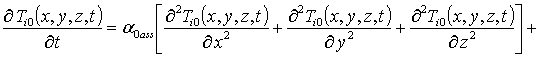
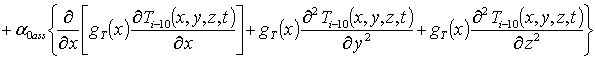, i ³1

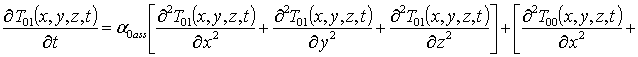
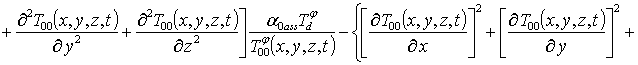
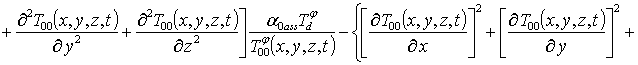
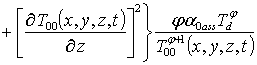                                   (9)

.

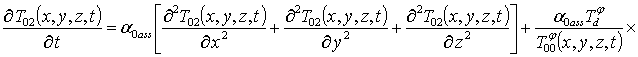
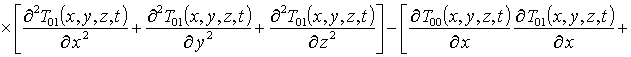
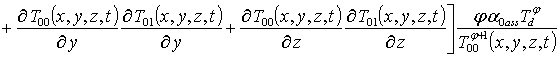
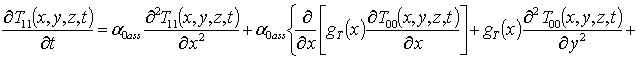
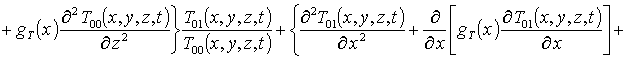
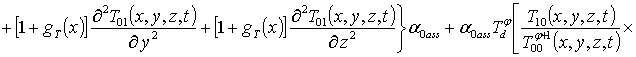
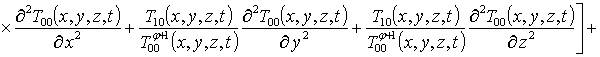
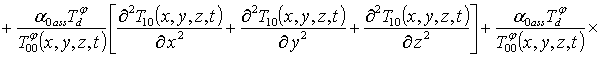
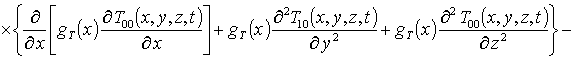
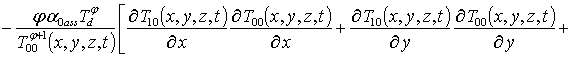
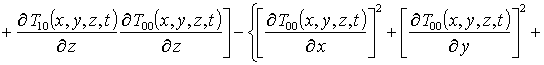
Подстановка ряда (8) в граничные и начальное условия (7) преобразует их к граничным и начальным условиям для функций T_ij(x,y,z,t)

, , , ,

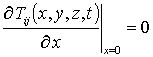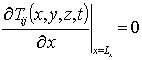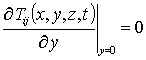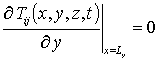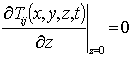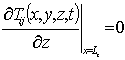, , T₀₀(x,y,z,0)=f_T(x,y,z), T_ij(x,y,z,0)=0, i ³1, j ³1.(10)

Решение уравнений (9) с условиями (10) приводит к следующему результату

,

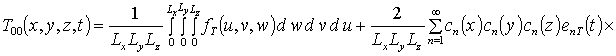
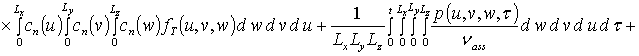
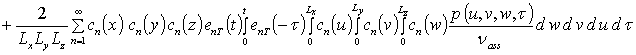где c_n(c) = cos (p nc/L), ;

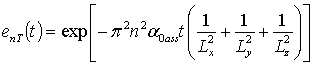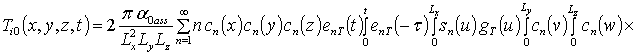
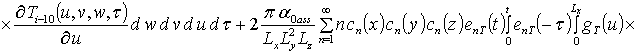
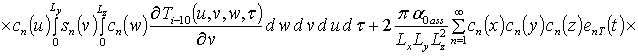
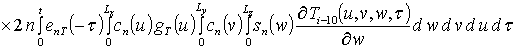, i ³1,

где s_n(c) = sin (p  n c/L);

;

;

.

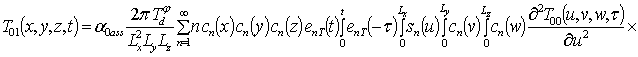
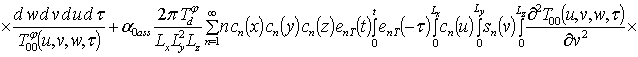
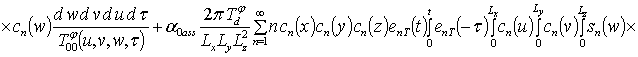
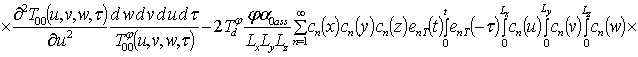
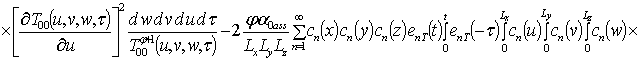
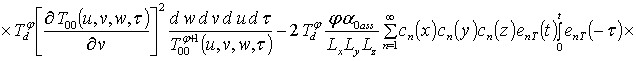
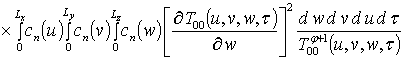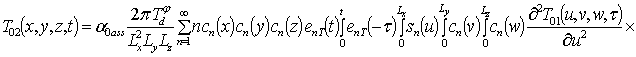
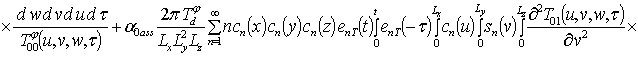
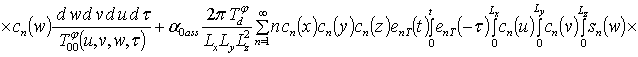
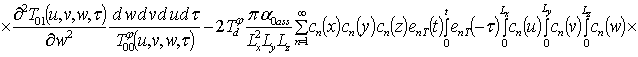
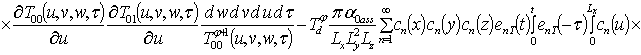
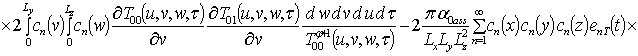
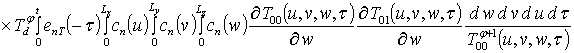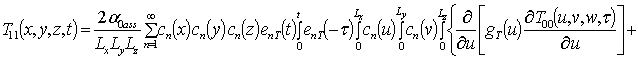
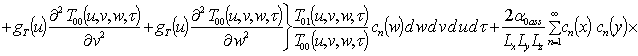
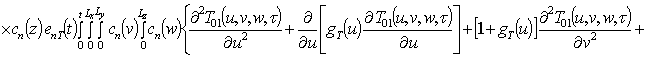
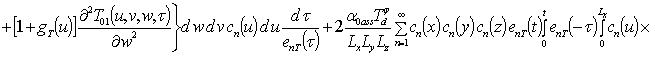
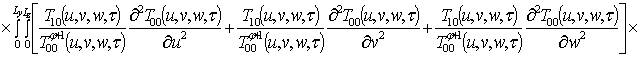
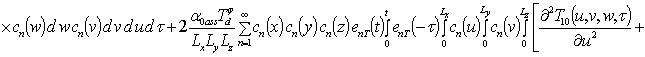
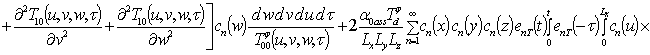
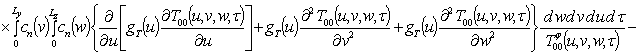
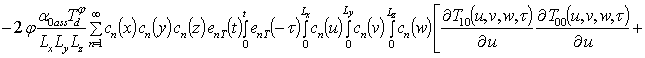
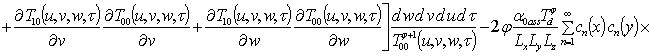
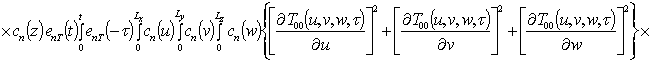
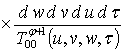Для качественного анализа пространственно-временного распределения температурного поля, а также для некоторых количественных оценок обычно достаточно его второго приближения по параметрам, используемым в разложении (см., например, [13,14]). Аналитические результаты позволили выявить и наглядно проиллюстрировать основные зависимости. Для уточнения полученных результатов использовались численные методы. Для определения пространственно-временного распределения радиационных дефектов, следуя [13,14], преобразуем коэффициенты диффузии (соответственно объемной и поверхностной) и параметр рекомбинации к следующему виду: D_rV(x,y,z,T)=D_0rV[1+e_rV g_rV(x,y,z, T)], D_rS(x,y,z,T)=D_0rS[1+e_rS g_rS(x,y, z,T)] и k_I,V(x,y,z,T)=k_0I,V[1+z h(x,y,z,T)], где D_0rV, D_0rS и k_0I,V – средние значения соответствующих величин, 0£e_rV <1, 0£e_rS <1, 0£z<1, | g_rV(x,y,z,T)|£1, | g_rS(x,y,z,T)|£1, |h(x,y,z,T)|£1. Перейдем к следующим безразмерным переменным: 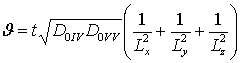, c = x/L_x, h = y/L_y, y = z/L_z, 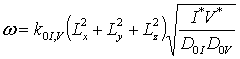, , 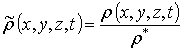,  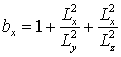, 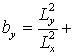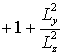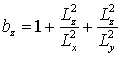. В новых переменных уравнения (4) принимают вид

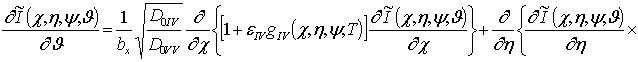
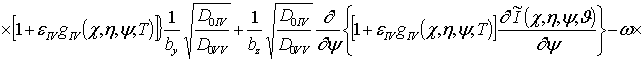
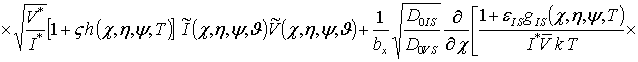
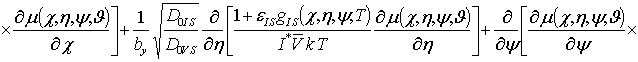
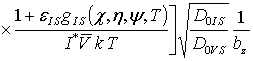                                 (11)

.

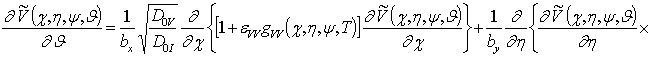
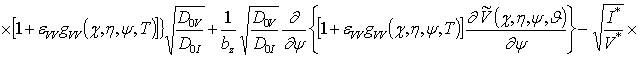
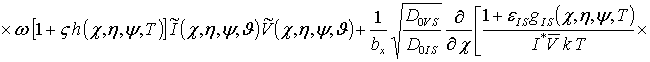
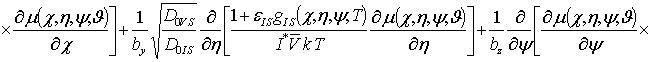
Решение уравнений (11) будем искать в виде степенных рядов

.                        (12)

Подстановка данного ряда в уравнения (11) позволяет получить систему уравнений для исходных приближений концентраций дефектов , а также поправочных функций к ним  (i³1, j³1, k³1) в следующем виде

 

;

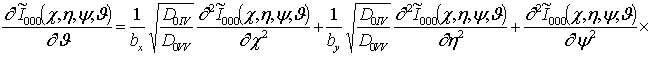
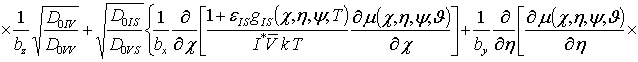
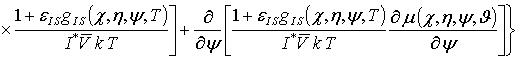
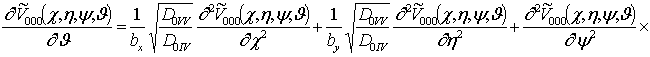
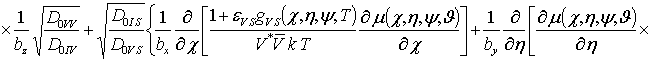
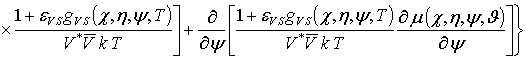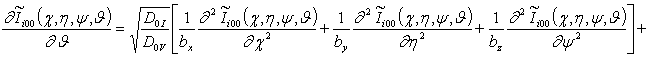
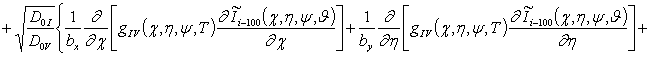
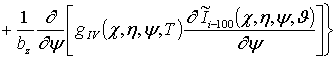
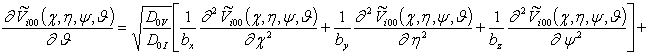
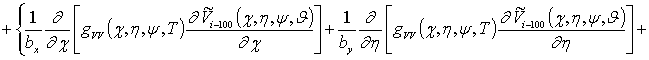
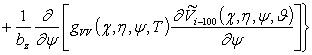, i ³1;

;

;

                                                                               

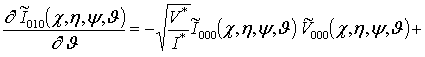
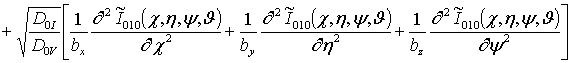
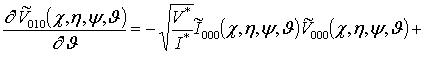
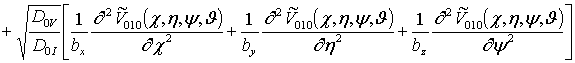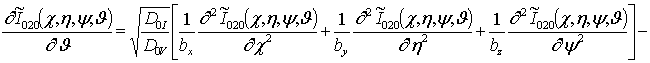
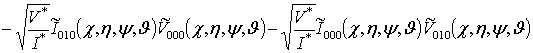
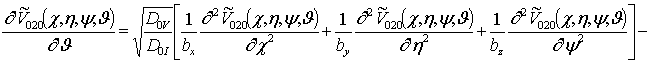
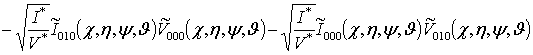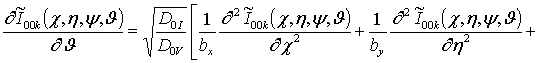
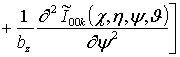
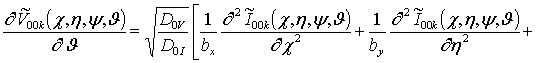
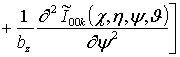                                                                                                                                                   ; (13)

;

;

.

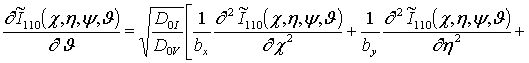
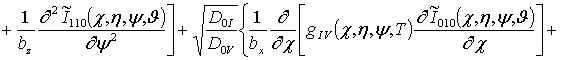
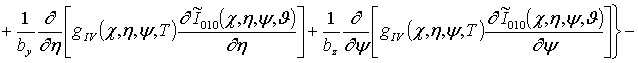
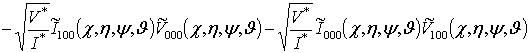
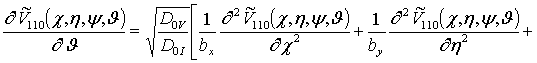
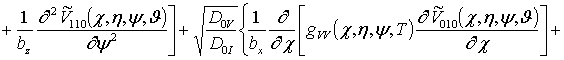
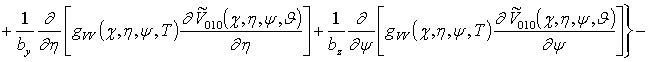
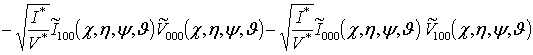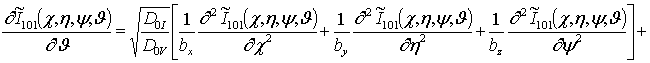
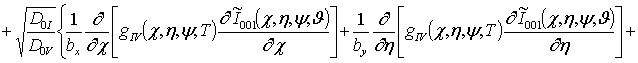
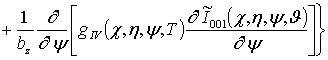
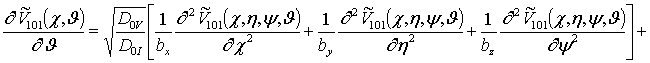
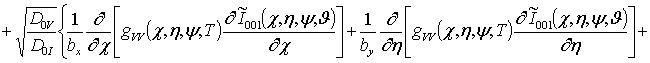
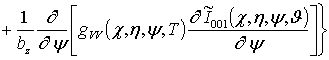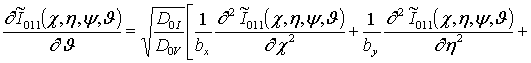
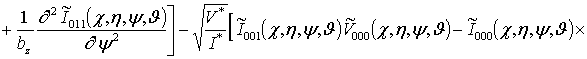
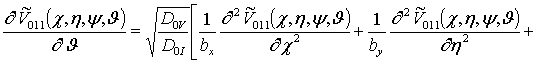
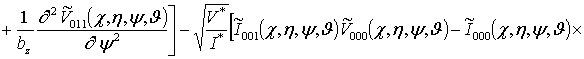
Подстановка рядов (12) в соответствующие граничные и начальные условия позволяет получить граничные и начальные условия для искомых функций

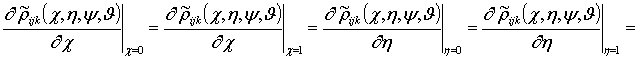
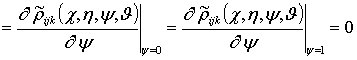, i ³1, j ³1, k ³1;

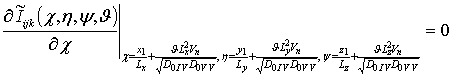, i ³0, j ³0, k ³0;

;

;

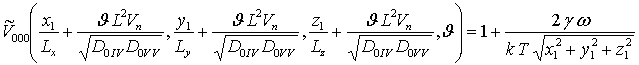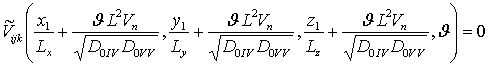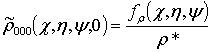; , i ³1, j ³1, k ³1.

Решениями уравнений (13) являются следующие функции

,

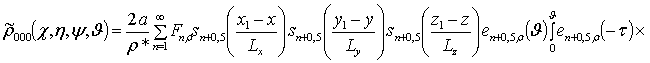
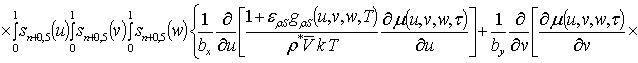
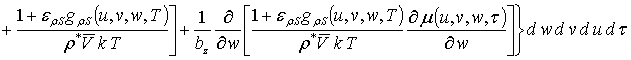где , s_n(d) = sin (p n d),

, ,

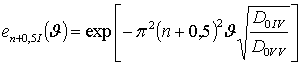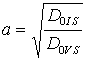 при r =V,  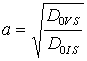при r =I;

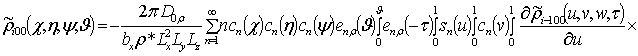
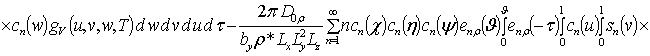
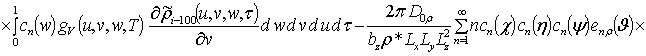
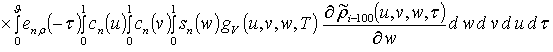, i ³1;

где c_n(d) = cos (p n d);

;

;

;

;

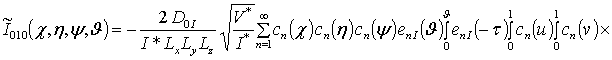
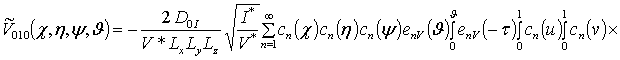
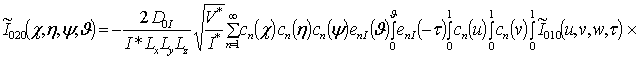
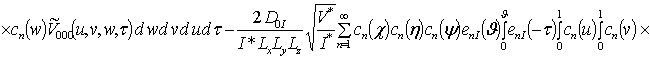
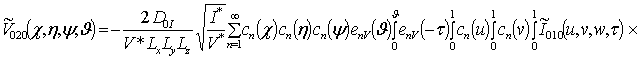
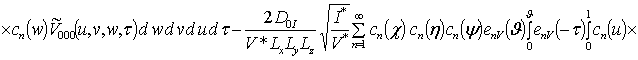
;       (14)

 

;

;

;

;

;

.

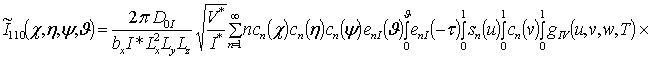
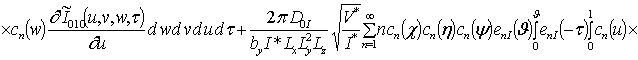
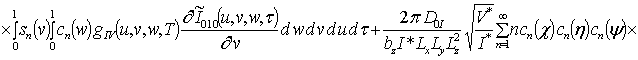
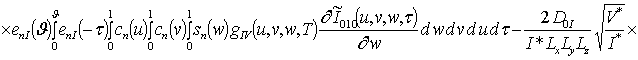
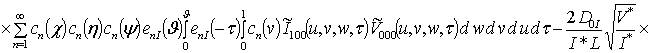
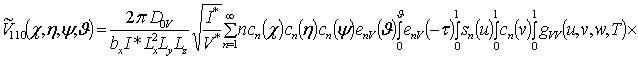
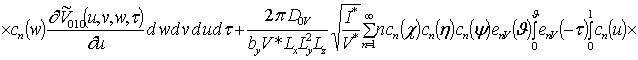
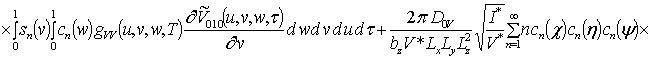
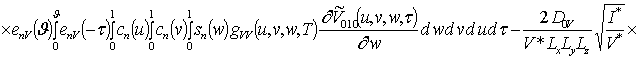
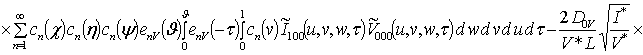
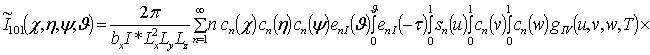
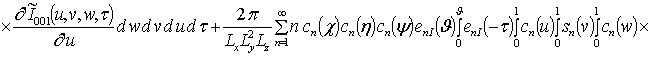
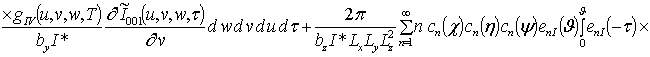
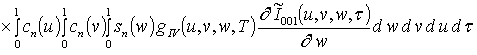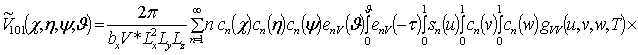
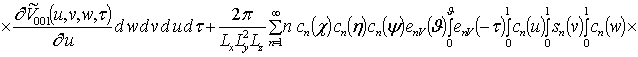
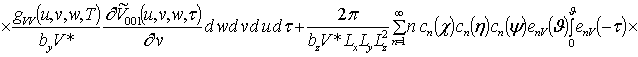
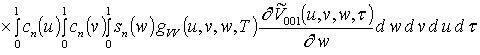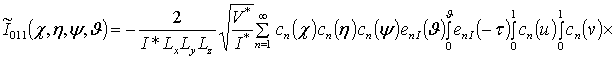
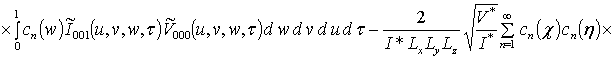
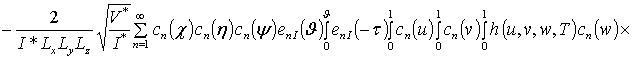
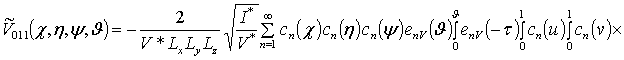
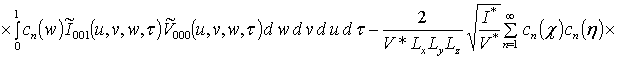
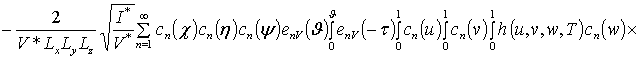
Анализ пространственно-временного распределения концентраций радиационных дефектов проводился аналитически во втором приближении по параметрам, используемым в соответствующем ряде, и уточнялся численно. Далее определим решение уравнения (1). Для этого, следуя [14,15],представим коэффициент диффузии D_L (x,y,z,T) в виде суммы D_L(x,y,z,T) =D_0L[1+e _L g_L(x,y,z,T)]. Решение уравнения (1) определим в виде следующего степенного ряда

.                            (15)

Подстановка данного ряда в уравнение (1) позволяет получить следующую систему уравнений для исходного приближения концентрации примеси C₀₀₀(x,y, z,t), а также поправочных функций к ней C_ijk(x,y,z,t) (i³1, j³1, k³1) в следующем виде

 

;

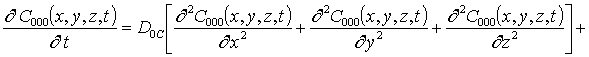
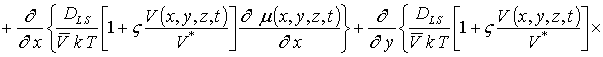
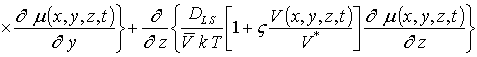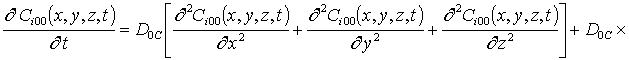
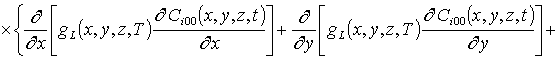
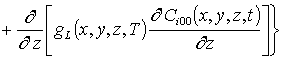, i ³1;

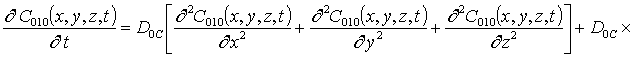
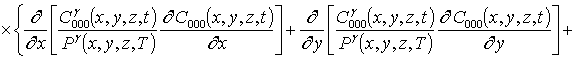
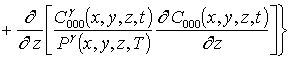;                              (16)

 

;

;

;

;

;

.

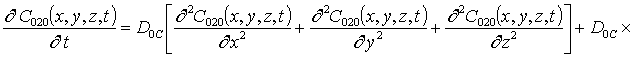
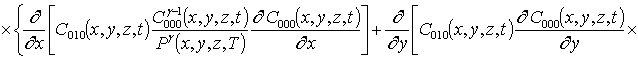
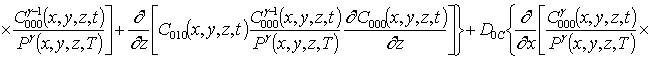
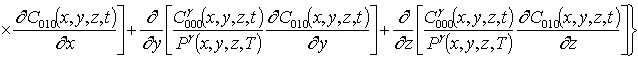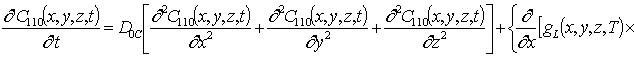
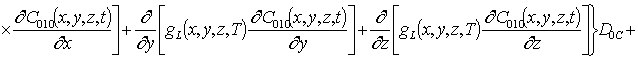
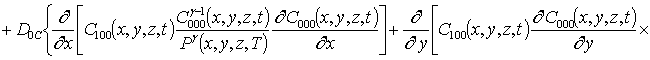
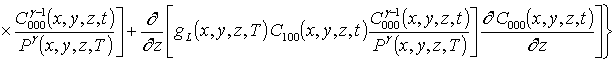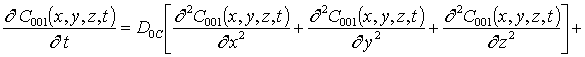
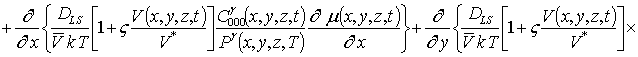
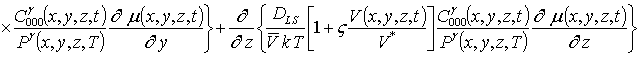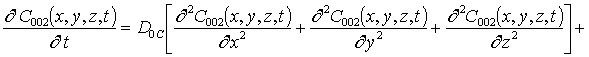
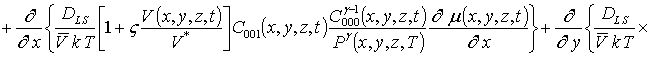
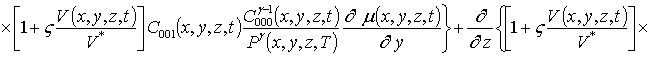
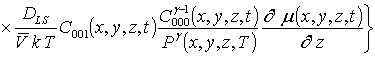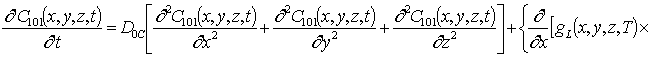
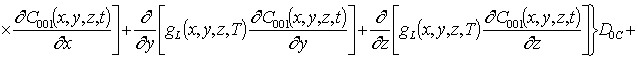
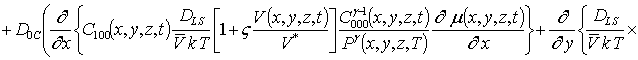
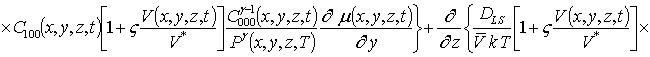
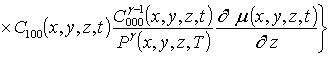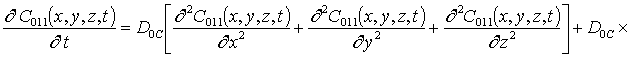
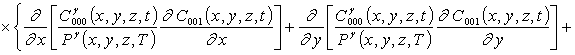
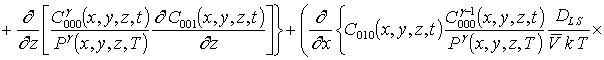
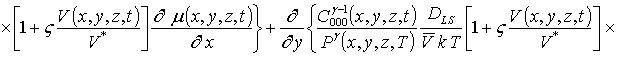
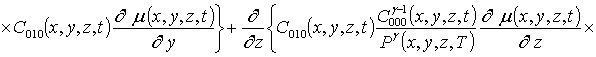
Подстановка ряда (15) в соответствующие граничные и начальные условия позволяет получить для искомых функций C_ijk(x,t)

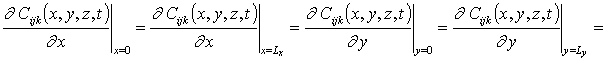
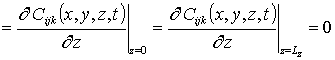; C₀₀₀(x,y,z,0)=f_C  (x,y,z); C_ijk(x,y,z,0)=0.

Решениями уравнений (16) являются следующие функции

,

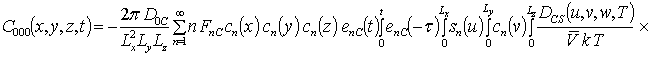
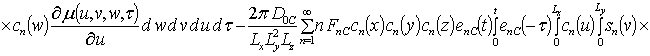
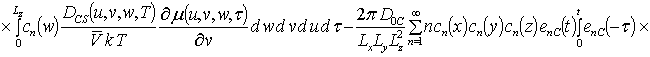
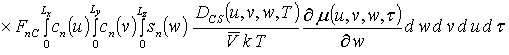где , ;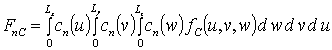

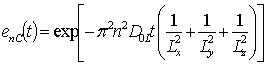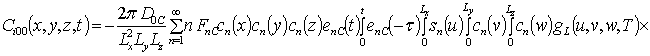
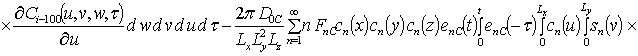
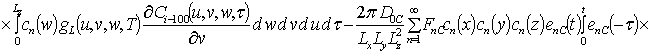
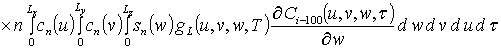, i ³1;

;

;

;

;

;

;

.

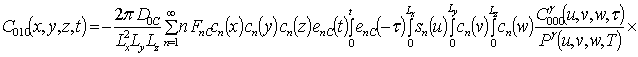
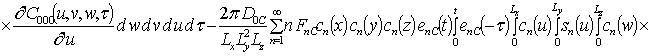
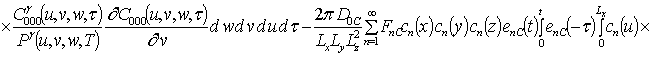
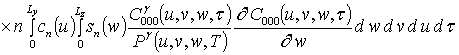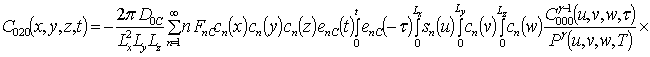
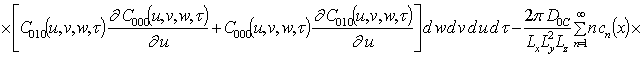
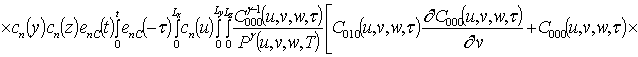
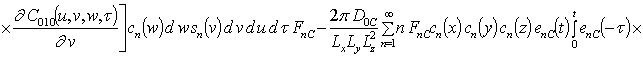
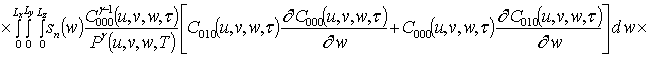
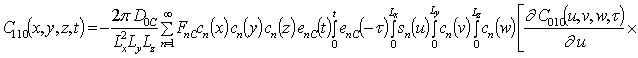
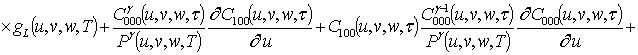
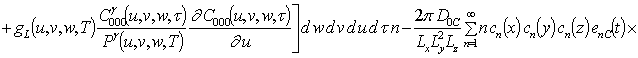
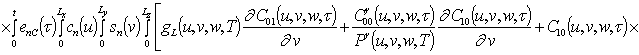
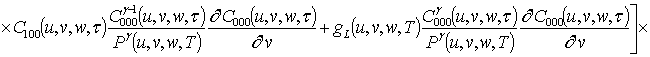
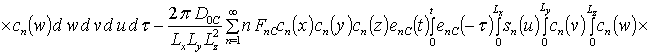
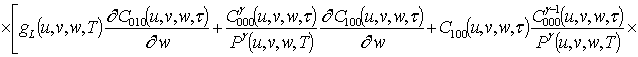
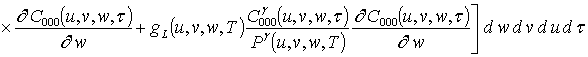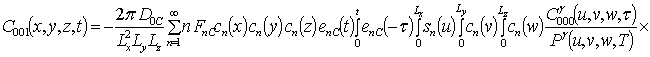
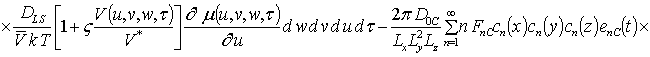
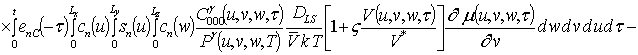
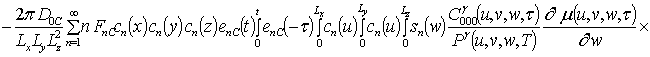
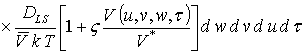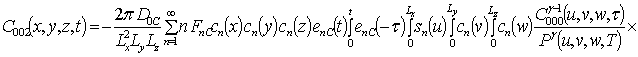
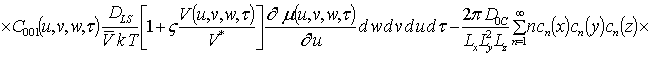
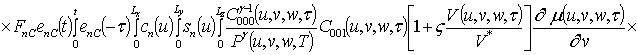
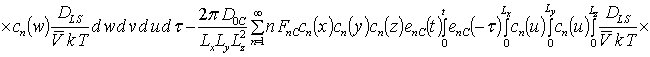
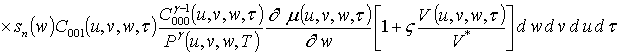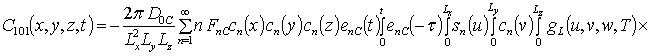
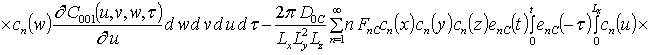
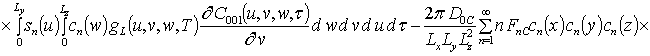
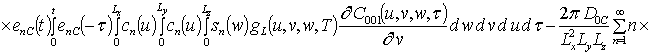
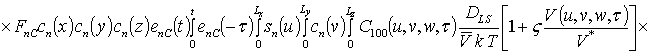
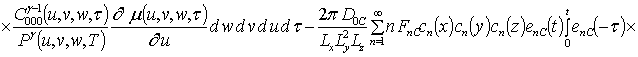
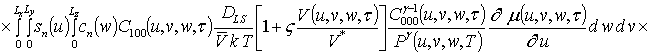
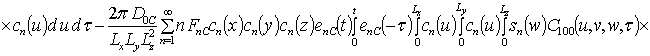
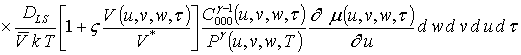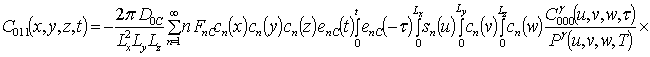
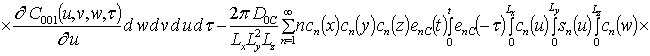
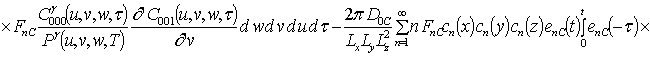
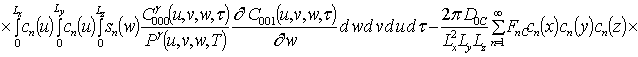
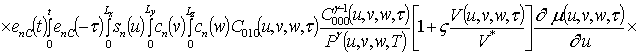
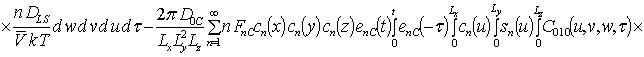
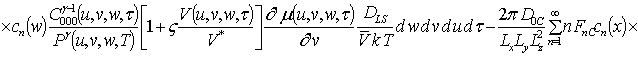
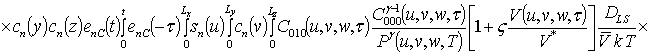
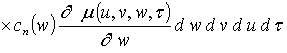Анализ пространственно-временного распределения концентрации примеси проводился аналитически во втором приближении по параметрам, используемым в соответствующем ряде, и уточнялся численно.

Результаты анализа

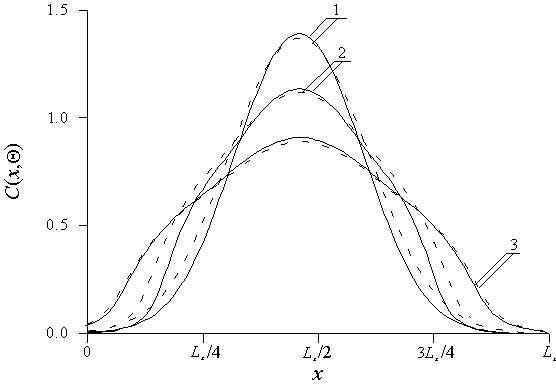
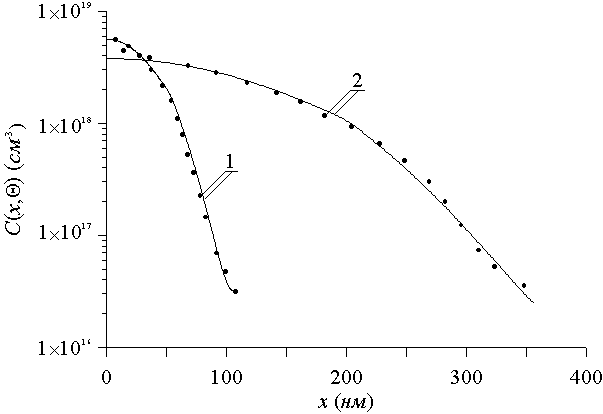
В данном разделе проведем анализ пространственно-временного распределения примеси в рассматриваемой Г (см. рис. 1) в течении микроволнового отжига радиационных дефектов. В течении отжига радиационных дефектов происходит уширение распределения примеси. Соотношение между энергией имплантируемых ионов и толщиной ЭС₁ целесообразно выбрать таким образом, чтобы после окончания отжига дефектов примесь достигла или почти достигла границ раздела между слоями Г. Если примесь в течении отжига дефектов не достигает границ раздела границ раздела между слоями Г, представляет интерес дополнительный отжиг примеси за время которого она достигнет данных границ раздела. Ранее было показано (см., например, [22]), что при оптимальной длительности отжига примесь достигает границ раздела между слоями Г практически не проникая вглубь соседних слоев. При этом в окрестности границ раздела формируются p-n-переходы. Полуотражающее свойство границ раздела позволяет увеличить резкость p-n-переходов и одновременно равномерность распределения примеси в легированной области (см. рис. 2). Сравнение расчетных распределений концентрации эрбия с экспериментальными распределениями (получены в [12]) в пористом и непористом SiC приведено на рис. 3. Ранее также было показано, что миккроволновый отжиг способствует увеличению резкости p-n-пе реходов и равномерности распределения примеси в легированной области [15]. Будем считать, что частота электромагнитного поля соответствует толщине скин -слоя, примерно равной суммарной толщине эпитаксиальных слоев. В этом случае данный отжиг наиболее эффективен для одновременного увеличения резкости p-n-переходов между ЭС₁ и П и равномерности распределения примеси в легированной области по сравнению с объемным отжигом. В результате отжига происходит трансформация пор (увеличиваются крупные поры за счет “рассасывания” мелких пор), что позволяет увеличить равномерность распределения примеси в пористой области [17].

 

Рис. 2. Распределения примеси в трехслойной гетероструктуре. Кривые 1 – распределения примеси в однородном материале. Кривые 2 - распределения примеси в трехслойной структуре с непористым ЭС₁. Кривые 3 - распределения примеси в трехслойной структуре с пористым ЭС₁. Сплошные кривые – аналитический расчет. Пунктирные кривые – численный расчет.

 

Рис. 3. Распределения концентрации примеси в пористом SiC и непористом SiC. Температура отжига 1700° C. Длительность отжига 120 мин. Сплошные линии – аналитическая аппроксимация, точки – экспериментальные данные из [12].

 

 

Далее проведем оптимизацию длительности отжига. Оптимальное значение длительности отжига определим, следуя [13-17, 22], из условия минимума среднеквадратической ошибки

                    (17)

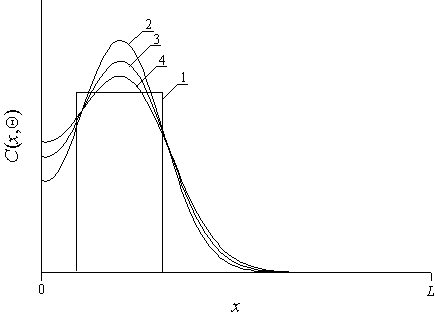
Рис. 4. Кривая 1 – идеализированное распределение примеси; кривые 2-4 – реальные распределения примеси в различные моменты времени, растущие с номером кривых.

 

 

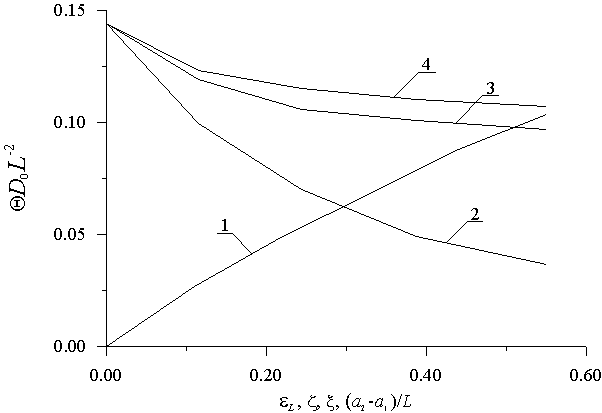
Рис. 5. Зависимость безразмерного компромиссного времени отжига J = QD₀/L², полученного из условия минимума функционала (17), от различных параметров ТС. Кривые 1-3 – зависимости J соответственно от e_L, z и x при нулевых значениях остальных двух параметров и (a₂-a₁)/L=1/2. Кривая 4 – зависимость J  от a/L при e =z=x=0.

 

аппроксимации реального распределения примеси C(x,y,z,t) и ее скачкообразной аппроксимацией y (x) (см. рис. 4). В результате минимизации функционала (17) получены зависимости оптимального значения длительности отжига от ряда параметров. Найденные зависимости приведены на рис. 5. Данный рисунок показывает, что с увеличением толщины ЭС₁ увеличивается оптимальная длительность отжига. Полученное увеличение происходит из-за того, что примеси требуется больше времени на достижение примесью границ раздела между слоями Г. С увеличением значений параметров e_L, z и x оптимальное значение длительности отжига уменьшается. Увеличение значений параметров e_L, z и x приводит к увеличению значений коэффициента диффузии и, как следствие, к ускорению диффузии примеси. Данное ускорение и приводит к уменьшению оптимальной длительности отжига.

Заключение

В данной работе рассмотрен способ увеличения компактности распределения примеси в имплантационном биполярном транзисторе, сформированном в полупроводниковой гетероструктуре, за счет использования полуотражающего свойства границ раздела. Одновременно с увеличением компактности распределения примеси происходит увеличение равномерности в легированной области путем использования полуотражающего свойства границ раздела, а также пористости слоев гетероструктуры и постимплантационного микроволнового отжига радиационных дефектов.

 

Данная работа поддержана грантом президента России (проект № МК-548.2010.2).

Литература

 

[1] A.B. Grebene. Bipolar and MOS analogous integrated circuit design. New York, John Wyley and Sons, 1983, 894p.

[2] З.Ю. Готра. Технология микроэлектронных устройств. - М.: Радио и связь. 1991. 528с.

[3] В.И. Лачин, Н.С. Савелов.Электроника. Ростов-на-Дону:Феникс, 2001.446 с.

[4] С.Т. Шишияну, Т.С. Шишияну, С.К. Райлян. ФТП. 2002. Т.36 (5). С. 611-617.

[5] Ю.М. Покотило, А.Н. Петух, В.В. Литвинов, Письма в ЖТФ Т. 29 (19), С. 26-30 (2003).

[6] T. Ahlgren, J. Likonen, J. Slotte, J. Risnen, M. Rajatore, J. Keinonen. Phys. Rev. B. 1997. V.56, (8). P. 4597-4603.

[7] Н.И. Волокобинская, И.Н. Комаров, Т.В. Матюхина, В.И. Решетников, А.А. Руш, И.В. Фалина, А.С. Ястребов. ФТП. 2001. Т.35 (8). С. 1013-1017.

[8] Ю.В. Быков, А.Г. Еремеев, Н.А. Жарова, И.В. Плотников, К.И. Рыбаков, М.Н. Дроздов, Ю.Н. Дроздов, В.Д. Скупов // Известия вузов. Радиофизика. 2003. Т.43, №3. С. 836-843.

[9] K.K. Ong, K.L. Pey, P.S. Lee, A.T.S. Wee, X.C. Wang, Y.F. Chong // Appl. Phys. Lett. 2006. Т.89, №17. С. 172111-172114.

[10] В.В. Козловский. Модифицирование полупроводников пучками протонов. Санкт-Петербург: “Наука”, 2003. 268 с.

[11] Е.И. Зорин, П.В. Павлов, Д.И. Тетельбаум. Ионное легирование полупроводников. М.: Энергия. 1975. 130 с.

[12] М.Г. Мынбаева, А.А. Лаврентьев, Е.Н. Мохов, К.Д. Мынбаев. Письма в ЖТФ, 34 (17), 13 (2008).

[13] E.L. Pankratov. Phys. Rev. B. 2005. V.72 (7). P. 075201-075208.

[14] E.L. Pankratov, B. Spagnolo. The Eur. Phys. J. B. 2005. V. 46 (1). P. 15-19.

[15] E.L. Pankratov. J. Appl. Phys. 2008. Vol. 103 (6). P. 064320-064330.

[16] E.L. Pankratov. J. Comp. Theor. Nanoscience. 2010. Vol. 7 (1). P. 289-295.

[17] E.L. Pankratov. Mod. Phys. Lett. B. In press.

[18] P.M. Fahey, P.B. Griffin, J.D. Plummer. Rev. Mod. Phys. 1989. V. 61. № 2. P. 289-388.

[19] M. Kitayama, T. Narushima, W.C. Carter, R.M. Cannon, A.M. Glaeser. J. Am. Ceram. Soc. 83, 2561 (2000); M. Kitayama, T. Narushima, A.M. Glaeser. J. Am. Ceram. Soc. 83, 2572 (2000).

[20] П.Г. Черемской, В.В. Слезов, В.И. Бетехтин. / Поры в твердом теле. – М.: Энергратомиздат, 1990. – 376 с.

[21] К.В. Шалимова. Физика полупроводников. М.: Энергоатомиздат, 1985. 391 с.

[22] E.L. Pankratov. Phys. Lett. A. 2008. Vol. 372 (11). P. 1897-1903.