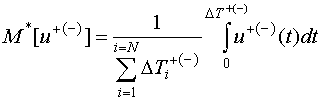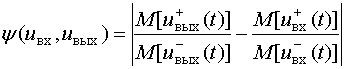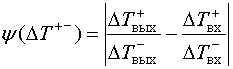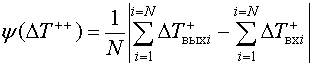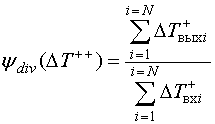УДК 621.317                                                              

ОПРЕДЕЛЕНИЕ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ СИГНАЛОВ ПО ИЗМЕРЕНИЯМ ВО ВРЕМЕННОЙ ОБЛАСТИ

Г. Р. Аванесян
 

Центр космической связи «Медвежьи озера» ОАО «ОКБ МЭИ», Москва

Получена 25 февраля 2011 г.

 

Аннотация. Показано, что задача определения нелинейных искажений сигналов может быть сведена к измерениям только во временной области. Предложены критерии и алгоритмы оценки нелинейных искажений, позволяющие получать результат для сигналов произвольной формы и обеспечивающие возможность определения нелинейных искажений в цепях, находящихся в рабочем режиме, без применения тестовых моногармонических сигналов.

Ключевые слова: временной интервал, нелинейные искажения, оценка, полуволна, случайный сигнал.

Abstarct. It is shown that the problem of determination of non-linear distortions of signals can be shown to measurements only in time area. The criterions and algorithms of an evaluation of the non-linear distortions permitting to receive an outcome for signals of any form and which have supplied a capability of determination of non-linear distortions in circuits, located in a working mode without application of test monoharmonic signals are offered.

Key words: a time interval, non-linear distortions, evaluation, half-wave, random signal.

 

Процесс определения нелинейных искажений, согласно сформировавшейся за многие десятилетия парадигме, заключается в выявлении в выходном сигнале цепи гармонических составляющих и оценки их суммарной мощности, в предположении, что при отсутствии искажений их быть не должно. У такого подхода есть существенный неустранимый недостаток – он не позволяет определять искажения сигналов со спектром, отличным от спектра тестового моногармонического сигнала. То есть он не позволяет определять искажения реальных случайных сигналов, переносящих полезную информацию. Причем широкоприменяемые, на протяжении уже более полувека, показатели нелинейных искажений – коэффициенты гармоник и интермодуляции – не являются показателями искажений рабочих сигналов, а служат всего лишь для получения прогностической информации о возможных искажениях в цепи, по результатам тестирования этой цепи детерминированным сигналом. Применять упомянутые показатели для оценки искажений реальных сигналов с произвольным спектром невозможно в принципе, так как они предполагают наличие строго моно- или  бигармонического воздействия. Проблема известна давно, но, к сожалению, на сегодняшний день не решена, несмотря на то, что один из первых методов (метод динамического спектра) был предложен еще в 50-х годах прошлого века, но не получил широкого распространения из-за необратимых потерь некоторого количества информации, вызванных необходимостью удаления участка спектра входного сигнала [1]. Попытки использовать для этих целей взаимокорреляционный анализ рабочих входного и выходного сигналов цепи, вносящей искажения, также не увенчались ожидаемым успехом, в первую очередь из-за трудности осуществления автоматической компенсации задержки сигнала при прохождении через исследуемую цепь. Кроме того, существует мнение, спорное, что корреляционная функция малочувствительна к нелинейным искажениям. Хотя более корректным было бы считать, что в данном случае проблема состоит в сложности реализации коррелятора с разрешением, которое позволило бы получить эффективный инструмент определения нелинейных искажений.

В настоящей статье описан принципиально новый подход, позволяющий определять нелинейные искажения случайных сигналов по косвенным измерениям только во временной области. Идея метода, впервые описанного в [2], состоит в следующем.

При нелинейном преобразовании различные по величине возмущения вызывают различную реакцию цепи на эти возмущения, изменяя исходные соотношения между мгновенными значениями сигнала. В частности, при монотонной нелинейной характеристике с меняющейся производной, положительная и отрицательная составляющие сигнала будут усиливаться по-разному, в зависимости от крутизны нелинейной характеристики цепи. Следовательно, если разделить знакопеременный процесс на положительную и отрицательную составляющие и определить как меняется отношение математических ожиданий знаковых составляющих после прохождения цепи, по предположению, вносящей искажения, то по изменению этого отношения можно будет судить о вносимых искажениях. Здесь важно уточнить, что речь идет о математическом ожидании только положительных или отрицательных значений сигнала без учета участков с нулевыми значениями. То есть   оценка математического ожидания в нашем случае находится не как результат усреднения сепарированной части процесса за все время его действия, а только за время действия полуволн u^+(-)(t) соответствующего знака ∆T ^+(-). Выражение для искомой оценки математического ожидания имеет вид:

,                                   (1)

где  – длительность i - ой полуволны.

В формуле (1) верхний предел интегрирования, в предположении, что отсчет времени начинается с нуля, может определяться как текущим временем, определяющим длительность реализации, так и упомянутой суммой .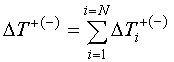 

  Основываясь на выявленных особенностях, числовым показателем нелинейных искажений будем считать величину, принимаемую за исходную:

,                                     (2)

где 

u⁺_вх(t), u^-_вх(t) – положительная и отрицательная составляющие входного сигнала u_вх(t), представляющего собой знакопеременный процесс с нулевым средним;

u⁺_вых(t), u^-_вых(t) – положительная и отрицательная составляющие выходного сигнала u_вых(t), представляющего собой знакопеременный процесс с принудительно удаленной постоянной составляющей после нелинейного преобразования.

При отсутствии нелинейных искажений показатель y(u_вх, u_вых) равен нулю, так как в этом случае выполняется равенство

,

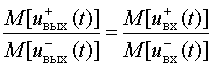и отличен от нуля при наличии нелинейных искажений.

Представим далее критерий (2), заменяя обозначения математических ожиданий выражениями для их оценки (1), в виде: 

,                   (3)

где

,  , , 

, ,

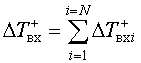N – количество положительных полуволн за время анализа T;

M – количество отрицательных полуволн за время T;

,  – длительность i-ой положительной полуволны соответственно входного и выходного сигналов;

, – длительность i-ой отрицательной полуволны соответственно входного и выходного сигналов.

Поскольку у сигналов с нулевым средним соблюдается равенство площадей, ограниченных отдельно положительными и отрицательными составляющими, выражение (3) можно существенно упростить и записать в виде:

.

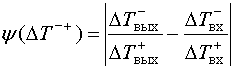Учитывая, что мы находимся на этапе выбора критерия и понимая, что замена в приведенной формуле дробей на обратные не изменит концепцию измерений, окончательно критерий представим в более привычной форме с точки зрения расположения положительных (вверху) и отрицательных (внизу) значений:

                                                 (4)

или

 .                            (5)

Из формул (4), (5) ясно видно, что процесс оценки нелинейных искажений можно свести к измерению временных интервалов и нескольким арифметическим операциям. Следовательно, можно утверждать, что в случае монотонной нелинейной характеристики информация о нелинейных искажениях центрированного знакопеременного процесса заложена в изменениях временных параметров, а именно, в изменении длительностей его полуволн. Подчеркнем, что если бы из выходного сигнала не удалялась, неизбежно появляющаяся при нелинейном усилении, постоянная составляющая, то переход от (3) к (4) был бы невозможен. С физической точки зрения изменение длительностей полуволн при нелинейном усилении сигнала с нулевым математическим ожиданием в цепи с монотонной нелинейной характеристикой объясняется тем, что неравномерное усиление различных участков сигнала, приводящее к перераспределению энергии, приводит еще и к появлению постоянной составляющей, в процессе принудительного удаления которой происходит «выравнивание» площадей положительной и отрицательной составляющих сигнала. При этом «выравнивание» происходит за счет изменения длительностей полуволн.

При необходимости от критерия (5) можно перейти к нормированному показателю 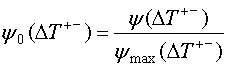, который принимает значения в диапазоне от нуля до единицы. Для этого воспользуемся неравенством Минковского, согласно которому

,

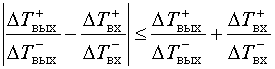следовательно                           

.

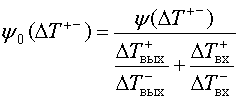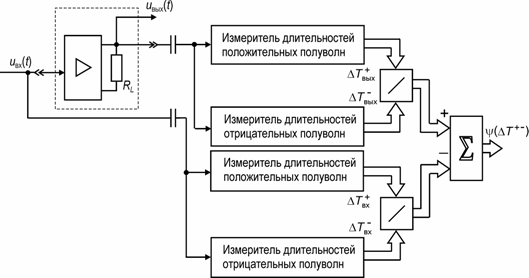
Алгоритм (5) реализуется в устройстве (рис. 1), основу которого составляют измерители временных интервалов. Штриховыми линиями на рис. 1 выделен четырехполюсник, вносящий искажения. Измерение временных интервалов и накопление результатов за время наблюдения для получения значений ,  и , осуществляется традиционным путем суммирования отсчетов, поступающих с периодом Т₀, в двоичных счетчиках. Далее в блоке вычитания находится разность

 .

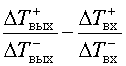Выделение модуля происходит принятыми в цифровой схемотехнике несложными приемами.
 

 

Рис. 1. Измеритель нелинейных искажений, реализующий метод сравнения длительностей разнополярных составляющих.

 

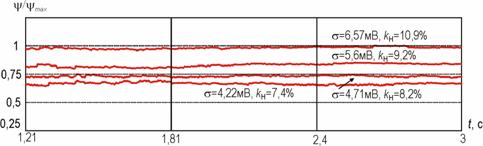
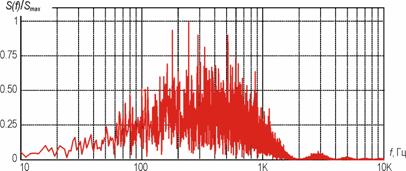
Результаты измерения нелинейных искажений при помощи вышерассмотренного устройства (см. рис. 1) представлены на графике рис. 2, отражающем  зависимость показателя y(∆Т ^+–) как от вносимых искажений, так и от времени. Искажения вносились в сигнал, представляющий собой стационарный гауссовский процесс с нулевым математическим ожиданием и спектром, показанным в нормированном виде S(f )/S_max, на рис. 3. Создавались искажения усилительным каскадом, имеющим характеристику в виде монотонно возрастающей нелинейной функции, при четырех уровнях входного сигнала, со среднеквадратическими значениями    s₁ = 4,22 мВ, s₂ = 4,71 мВ, s₃ = 5,6 мВ, s₄ = 6,57 мВ. Возникающая, при различных уровнях входного сигнала, нелинейность в количественном отношении определяется коэффициентом нелинейности k_Н, который вычислялся традиционным способом по эмпирически полученной передаточной характеристике цепи путем ее сравнения с прямой линией, проведенной как касательная в окрестности нуля. Верхняя граница диапазона изменений  k_Н определялась началом ограничения. Результаты вычисления коэффициентов нелинейностей k_Н показаны рядом с соответствующими графиками на рис. 2. Временные интервалы измерялись с дискретом Т₀ = 1 мкс. Из графиков легко видеть закономерный рост показателя y(∆Т ^+–) с увеличением коэффициента нелинейности k_Н. Кроме того, развертка меры y(∆Т ^+–) во времени свидетельствует о снижении погрешности оценки с увеличением длительности реализации процесса, а также о ее состоятельности. Это ясно видно из сравнения размеров флуктуаций величины y(∆Т ^+–) на начальном и конечном временных отрезках.
 

Рис. 2. Результаты измерений показателя  нелинейных искажений как функции от времени, соответствующие различным искажениям.

 

Рис. 3. Спектр сигнала на входе четырехполюсника, вносящего искажения.

 

Связь критерия (4) с нелинейностью цепи иллюстрируется графиками, представленными на рис. 4.  Показаны два случая (y/y_max1 и  y/y_max2) определения зависимости оценки y(∆Т^+–) от объема нелинейных искажений, отличающихся диапазоном вносимых искажений с сохранением количества экспериментально определенных отсчетов, что позволяет детализировать связь при малых значениях k_Н. Стандартное отклонение от линейной зависимости (штриховые линии на рис. 4) в диапазоне нелинейностей 1,41…10,9% составило 0,021, в диапазоне 1,41…7,01%  – 0,31.

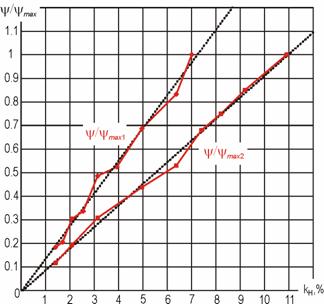
Рис. 4. Зависимость показателя  нелинейных искажений от

коэффициента нелинейности цепи.

 

Для нахождения погрешности оценки показателя нелинейных искажений y(∆Т ^+–)  покажем случайную погрешность, выраженную в виде дисперсии D[y*], как следующую сумму

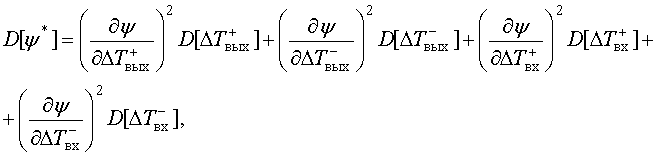
где

 – дисперсии оценок временных интервалов DT.

 

После вычисления модулей частных производных имеем:

 

,  , ,  .

 

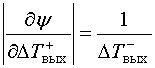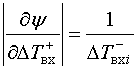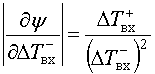Подставляя найденные коэффициенты влияния в вышеприведенную формулу для вычисления погрешности и учитывая, что дисперсии оценок временных интервалов DT при неизменном периоде Т₀ счетных импульсов равны друг другу, а также исходя из того, что упомянутые  дисперсии D[∆Т]  равны Т²₀/12 [3], получим

.

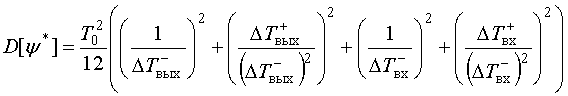Как видим, погрешность оценки нелинейных искажений по предложенному критерию зависит только от дискрета отсчета временных интервалов Т₀ и их размеров. То есть повышение точности достигается как уменьшением величины Т₀, так и увеличением длительности реализации процесса.

Закономерным является возникающий в связи с вышеизложенным вопрос: если информация о нелинейных искажениях заложена в изменениях длительностей полуволн, то, может быть, есть смысл сравнивать только длительности полуволн одного знака входного и выходного сигналов, что безусловно должно упростить как алгоритм измерений, так и аппаратуру. Это действительно возможно. Вместо критерия y(∆T ^+-) (4) можно применить величину, определяемую как среднее значение модуля разности

                                     (5)

или как среднюю абсолютную разность сумм

                                        (6)

Обе формы равноценны, но отличаются количеством операций и порядком их выполнения. В первом случае для получения результата требуется выполнить N (или M) вычитаний и столько же сложений с накоплением результатов. Во втором случае – 2N (или 2М) сложений с накоплением и одно вычитание.

Переход от алгоритма (4) к (5) или (6), конечно, позволяет упростить как аппаратурную часть измерителя, так и программную [4]. Однако упрощение приводит к появлению такого недостатка, как зависимость результатов измерений от характеристик сигналов. Это связано с тем, что разность длительностей полуволн зависит от их абсолютных значений, а значит, от спектральных свойств исследуемых сигналов. Чем больше длительность полуволны, тем на большую величину при неизменных нелинейных искажениях изменяется указанная длительность и наоборот. Несколько уменьшить эту зависимость можно, если вместо разности измеренных интервалов ввести их отношение

.                                          (7)

В этом случае

,

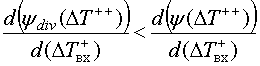т. е. снижение вышеуказанной зависимости определяется более низкой чувствительностью алгоритма (7). Кроме снижения чувствительности усложняется еще и реализация алгоритма – как программная, так и аппаратная. По этим причинам критерий (7) нельзя считать безусловной альтернативой критериям (5), (6), а при применении критерия следует исходить из конкретных задач и возможностей реализации алгоритмов.

При применении критериев (5) – (7) для снижения зависимости результатов измерений от спектров сигналов необходимо строго оговаривать диапазон частот сигналов, участвующих в измерениях и одновременно сужать этот диапазон до уровня, определяемого допустимыми погрешностями. Поэтому предпочтительной областью применения критериев (5) – (7) является тестирование цепей узкополосными сигналами с заданными параметрами. Что же касается критерия (3), то он является универсальным, не зависит от спектров сигналов и рассчитан, главным образом, на выявление и оценку искажений случайных сигналов.

 

Выводы

1. Установлено, что при нелинейном преобразовании центрированного знакопеременного случайного процесса, в случае монотонной нелинейной характеристики цепи, изменяются соотношения между математическими ожиданиями сепарированных положительных и отрицательных составляющих процесса, найденных как результат усреднения за время действия всех полуволн соответствующего знака.  Это позволило обоснованно перейти от отношения математических ожиданий  к отношению суммарных длительностей полуволн различных знаков и впервые применить в качестве критерия нелинейных искажений величину, зависящую только от временных параметров исходного и искаженного сигналов. Следовательно, измерение нелинейных искажений может быть сведено к измерениям только во временной области, без применения многоразрядных АЦП, со значительным упрощением измерителей и без снижения точности измерений.

2. Поскольку предложенный метод позволяет определять нелинейные искажения случайных сигналов, то он применим не только как средство измерений, но и для решения задач непрерывного контроля состояния цепей и/или качества выходных сигналов без вмешательства в работу цепей, что широкоприменяемые методы не могут обеспечить в принципе.
 

Литература

1.     А. с. СССР 90158. Способ измерения нелинейных искажений / В. М. Вольф. – Заявл. 10.01.1950.

2.     Пат. RU 2244314. Способ статистической оценки нелинейных искажений и устройство для его реализации / Г. Р. Аванесян. – Опубл. 10. 01. 2005, Бюл. № 1.

3.     Кончаловский В. Ю. Цифровые измерительные устройства. – М.: Энергоатомиздат, 1985.

4.     Пат. RU 2247997. Измеритель нелинейных искажений случайных сигналов / Г. Р. Аванесян. – Опубл. 10. 03. 2005, Бюл. № 7.