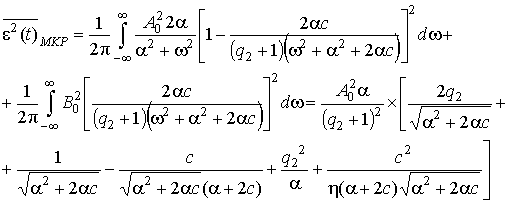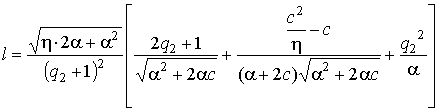УДК 681.513.6
АДАПТИВНЫЙ КОМПЕНСАТОР ПОМЕХ НА
ОСНОВЕ ФОРМИРОВАНИЯ МОДЕЛЕЙ СЛУЧАЙНЫХ ПРОЦЕССОВ
А. Е. Манохин, Ю.
А. Нифонтов
Институт радиоэлектроники и информационных технологий-РТФ УрФУ им. первого Президента РФ Б.Н.Ельцина, кафедра радиоэлектронных и телекоммуникационных систем, Екатеринбург
Получена 28 декабря 2010 г., после доработки – 27 февраля 2011 г.
Аннотация. В работе представлен адаптивный компенсатор помех, основанный на формировании моделей сигналов и помех, являющихся стационарными случайными процессами. Разработанный адаптивный компенсатор работоспособен в условиях слабой взаимной корреляции или абсолютной некоррелированности помех на обоих его входах.
Ключевые слова: модельный компенсатор помех, формирующий белый шум, оптимальный фильтр.
Abstract. Adaptive equalizer of disturbances, based on the models of signals and disturbances, which are stationary random processes, is described in this paper. This equalizer can operate under conditions of weak mutual correlation or the lack of correlation of disturbances on its both inputs.
Keywords: modeling equalizer of disturbances forming white noise, optimal filter.
Введение
Адаптивная компенсация помех представляет собой способ оптимальной фильтрации, который можно применять всегда, когда имеется подходящий эталонный входной сигнал. Принципиальными достоинствами этого способа являются инвариантность схемы по отношению к классу сигналов и их параметрам, низкий уровень помех на выходе и малые вносимые искажения сигнала. Этот способ приводит к устойчивой системе, которая автоматически отключается, если не происходит улучшения отношения сигнал-шум [1]. В автокомпенсаторах помех с применением адаптивного фильтра эффективное подавление помехи происходит только тогда, когда помеховые составляющие на обоих входах автокомпенсатора взаимно коррелированны.
Предлагаемый адаптивный компенсатор помех отличается от своих предшественников тем, что условие взаимной коррелированности помех, действующих на основном и дополнительном входах компенсатора, не соблюдается.
Модельный компенсатор помех
Алгоритм работы предложенного адаптивного автокомпенсатора помех (в дальнейшем, модельный компенсатор помех - МКП) основан на алгоритме формирования адаптивных моделей случайных процессов [2]. В основе синтеза алгоритма формирования адаптивных моделей случайных процессов лежит схема классического винеровского фильтра.
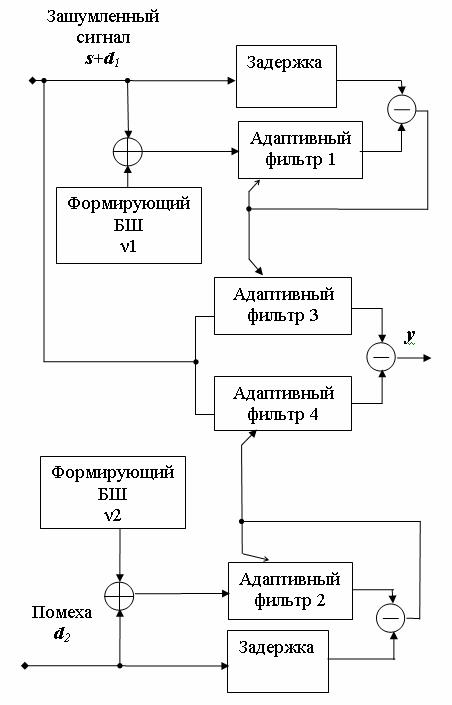
Модельный компенсатор (рис.1) состоит из двух идентичных каналов: сигнального, на входе которого присутствует смесь сигнала и помехи, и компенсационного, на который подается помеха. Каждый из каналов представляет собой формирователь модели сигнала [3].
Сигнальный канал предназначен для формирования модели зашумленного сигнала (смеси сигнала и помехи). Входным сигналом канала является зашумленный сигнал (s+d1). В процессе формирования модели (с помощью соответствующего алгоритма адаптации) перестраивается импульсная характеристика адаптивного фильтра 1 так, чтобы выходной сигнал фильтра имел наилучшее приближение к полезному сигналу (s+d1). В результате процесса адаптации коэффициент передачи АФ1 представляется в виде:
где Ss(ω) – спектральная плотность мощности сигнала;
Sd(ω) – спектральная плотность мощности помехи;
Sν(ω) – спектральная плотность мощности формирующего белого шума.
Рис.1. Структурная схема модельного компенсатора помех.
Другими словами, перестраивая весовые коэффициенты, тем самым формируется модель требуемого сигнала, представленная в виде коэффициентов фильтра АФ1.
Работа компенсационного канала идентична. В процессе работы алгоритма формирования весовых коэффициентов адаптивный фильтр 2 настраивается так, чтобы сигнал на выходе фильтра имел максимальное приближение к требуемой помехе d2. При этом формируется модель помехи d2[3]. В результате процесса адаптации коэффициент передачи АФ2 представляется в виде
Тогда результирующий коэффициент передачи модельного автокомпенсатора определяется из ф.1 и ф.2 как разность оптимальных коэффициентов передачи адаптивных фильтров АФ1 и АФ2:
Для того, чтобы выражение ![]() обратить в ноль, необходимо, чтобы отношение мощности помеха-формирующий
шум в сигнальном канале (q21) и отношение мощности помеха-формирующий
шум в компенсационном канале (q22) были равны. Т.е.
обратить в ноль, необходимо, чтобы отношение мощности помеха-формирующий
шум в сигнальном канале (q21) и отношение мощности помеха-формирующий
шум в компенсационном канале (q22) были равны. Т.е.
В этом случае ф.3 можно переписать как
Таким образом, модельный компенсатор является фильтром, параметры которого подстраиваются таким образом, чтобы эффективно подавить помеху.
Согласно формуле 5, при увеличении мощности формируемого белого шума до бесконечно большой величины, мощность выходного сигнала на выходе компенсатора уменьшается до нуля. В то же время при уменьшении значения мощности формирующего белого шума до нуля передаточные функции (1) и (2) вырождаются, и модельный компенсатор перестает осуществлять фильтрацию полезного сигнала.
В этой связи существует оптимальное отношение мощности помеха-формирующий шум в каналах. Найдем его через оценку проигрыша модельного компенсатора помех оптимальному фильтру по критерию минимальной среднеквадратичной ошибки.
Под оптимальным фильтром будем понимать линейный фильтр с постоянными параметрами, на входе которого действует сигнал s и помеха d1, имеющие гауссово распределение. Тогда дисперсия ошибки фильтрации на выходе оптимального фильтра [4]:
При вещественном характере коэффициента передачи модельного компенсатора помех дисперсию ошибки фильтрации можно оценить по формуле [5,с.53]:
Относительный проигрыш оптимальному фильтру выразим через l:
В качестве полезного сигнала рассмотрим гауссово-марковский процесс со спектральной плотностью
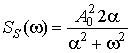
и помеху – белый гауссов шум с мощностью B02. Выбор гауссово-марковского процесса в качестве полезного сигнала обусловлен тем, что он во многих случаях является удобной математической моделью сообщений [6] и, в частности, хорошо аппроксимирует речевой сигнал [7].
Для упрощения вывода примем допущение, что мощности помех в каналах равны, тогда согласно формуле (4) мощности формирующего белого шума в каналах тоже должны быть равны.
Подставив спектральные плотности сигнала и помехи в (6), получим выражение для дисперсии ошибки оптимального фильтра:
где η – отношение мощности сигнал-помеха.
Аналогично находим дисперсию ошибки модельного компенсатора:
где
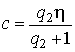 .
.
Подставляя выражения (9) и (10) в (8), находим проигрыш оптимальному фильтру:
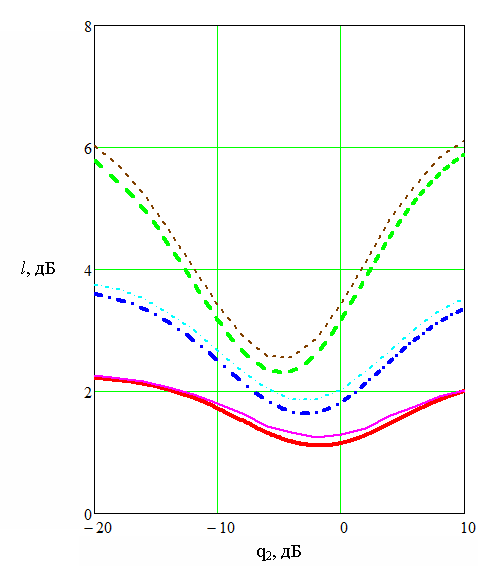
Анализируя изображенные на рисунке 2 расчетные зависимости проигрыша l от отношения помеха-формирующий шум при различных отношениях мощности сигнал-помеха (согласно ф.11), можно зафиксировать оптимальное значение q2, при котором проигрыш минимален.
Компьютерное моделирование
С помощью разработанного программного обеспечения «Модельный компенсатор помех» было проведено моделирование работы разработанного алгоритма подавления помех. Получены следующие результаты.
В экспериментах исследовалась зависимость проигрыша оптимальному фильтру l от отношения помеха-формирующий шум q2 и от отношения сигнал-помеха η. Параметры моделирования отображены в таблице 1, результаты моделирования показаны на рисунках 2 и 3. В качестве полезного сигнала был выбран марковский процесс. Помеха – белый гауссов шум, помехи в каналах некоррелированы.
Таблица 1. Параметры моделирования
|
Параметр |
Значение |
|
Ширина полосы сигнала (при α=0.105) |
3354 Гц |
|
Объем выборки для оценки l |
65536 |
|
Количество выборок для усреднения l |
10 |
|
Число весовых коэффициентов |
256 |
|
Коэффициент адаптации |
0,001 |
|
Алгоритм адаптации фильтров |
метод наименьших квадратов [1] |
Таблица 2. Расчетные и экспериментальные значения q2
|
Отношение сигнал-помеха η, дБ |
Расчетное значение q2, дБ |
Экспериментальное значение q2, дБ |
|
-10 |
-1.7 |
-2 |
|
-6 |
-2.9 |
-3 |
|
0 |
-4.8 |
-4 |
Рис.2. Зависимость проигрыша l от отношения помеха-формирующий шум q2 (расчетная – толстая линия, моделируемая – тонкая линия) при η=-10дБ (сплошная), η=-6дБ (штрихпунктирная), η=0дБ (пунктирная).
На рисунке 2 изображены зависимости проигрыша l от отношения помеха-формирующий шум (q2) при различных отношениях мощности сигнала и помехи, которые были получены из формулы 11 и в результате моделирования.
Анализируя график на рисунке 2, можно отметить, что для достижения максимально эффективного выделения полезного сигнала необходимо контролировать отношение мощности помеха-формирующий шум в обоих каналах (q2), добиваясь установки его оптимального значения, при котором проигрыш оптимальному фильтру минимален.
В таблице 2 отображены расчетные и экспериментальные значения q2, которые практически совпадают, что говорит о правильно применяемом математическом аппарате.

|
Рис.3. Зависимость проигрыша l от отношения сигнал-помеха η: расчетная (сплошная линия), моделируемая (штрихпунктирная линия) при q2 =-10дБ.
Выводы
Авторами разработан адаптивный компенсатор помех, который работоспособен в условиях взаимной некоррелированности помех на обоих его входах, что подтверждается результатами математических расчетов и моделирования. Эти результаты показывают, что при малых отношениях мощности помехи к мощности формирующего белого шума (менее минус 10дБ) модельный компенсатор помех можно считать квазиоптимальным фильтром. При этом в диапазоне изменения отношения мощности сигнал-помеха не более 0дБ проигрыш оптимальному винеровскому фильтру составляет не более 3.5дБ при изменении значения отношения мощности помехи к мощности формирующего белого шума от минус 10дБ до 0дБ.
Несмотря на имеющийся проигрыш, модельный компенсатор в отличие от оптимального фильтра почти не требует знания априорной статистической информации о сигнале и помехе, за исключением значений мощности зашумленного сигнала и мощности помехи в опорном канале. Кроме того, отклонение параметров сигнала и помехи от значений, принятых при синтезе оптимального фильтра, приводит к существенному ухудшению характеристик фильтрации, тогда как модельный компенсатор устойчив к подобным расстройкам.
Авторами при моделировании изложенного алгоритма компенсации применялись и другие виды полезных сигналов (узкополосный нормальный процесс, различные типы дискретных сигналов). При использовании этих полезных сигналов модельный компенсатор также показал хорошую работоспособность.
Литература
1. Уидроу Б., Стирнз С. Адаптивная обработка сигналов. Пер. с англ. – М.:Радио и связь, 1989. – 440с.
2. Манохин А.Е. Идентификация случайных процессов на основе формирования их адаптивных моделей.// Журнал научных публикаций аспирантов и докторантов, №9 – Курск: изд. ООО «Редакция Журнала научных публикаций аспирантов и докторантов», 2008. – с.238-241.
3. Манохин А.Е., Нифонтов Ю.А. О некоторых приложениях моделирования сигналов с использованием адаптивных фильтров // Радиолокация. Навигация. Связь. Труды десятой международной научно-технической конференции. Воронеж: изд. НПФ «Саквоее» ООО, 2004. С.54.
4. Гоноровский И.С., Демин М.П. Радиотехнические цепи и сигналы: Учеб.пособие для вузов. -5-е изд., перераб. и доп.-М.:Радио и связь, 1994.-480с.; ил.
5. Шахтарин Б.И. Фильтры Винера и Калмана. –М: Гелиос АРВ, 2008. 408с.: ил.
6. Шахтарин Б.И. Случайные процессы в радиотехнике. 4-е изд., перераб. и дополн. Т1. Линейные преобразования. –М: Горячая линия – Телеком, 2010. 520с.: ил.
7. Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем: Учеб. Пособие для вузов. – М.:Радио и связь, 2004. – 608с.:ил.

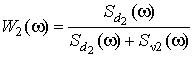

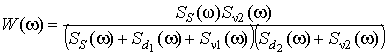
 (6)
(6)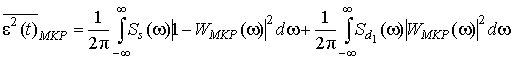

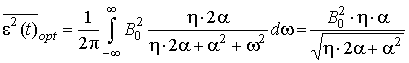 (9)
(9)