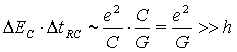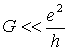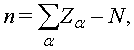УДК 621.382

ИССЛЕДОВАНИЕ СВЯЗИ ЭНЕРГЕТИЧЕСКИХ СПЕКТРОВ МОЛЕКУЛ С ТРАНСПОРТНЫМИ ХАРАКТЕРИСТИКАМИ ОДНОЭЛЕКТРОННЫХ ТРАНЗИСТОРОВ НА ИХ ОСНОВЕ

 

Я. С. Герасимов, В. В. Шорохов, А. Г. Маресов, Е. С. Солдатов, О. В. Снигирев

Физический факультет МГУ им. М.В. Ломоносова

 

Получена 12 февраля  2013 г.

 

Аннотация. Исследована взаимосвязь между энергетическим спектром молекулы и транспортными характеристиками мономолекулярного одноэлектронного транзистора на основе такой молекулы. Квантовыми методами рассчитаны одноэлектронные энергетические спектры малых молекул карборана C₂B₁₀H₁₂  и фуллерена C₆₀ для их основных и возбужденных зарядовых энергетических состояний, а также платинового молекулярного кластера. Установлены эффективные емкостные параметры, предложен параметрический подход для расчета положения электронных уровней в энергетическом спектре молекул. При помощи метода имитационного моделирования Монте-Карло рассчитаны транспортные характеристики мономолекулярного одноэлектронного транзистора.

Ключевые слова: молекулярная электроника, одноэлектронный транзистор, электронные наноустройства, дискретный энергетический спектр, диаграмма стабильности.

Abstract. The relationship of energy spectra of a molecule and transport charecteristics of single-electron transistor based on this molecule is studied. Electron energy spectra of small molecules of carboran C₂B₁₀H₁₂, fullerene C₆₀ and platinum molecular cluster are calculated by means of quantum methods for their ground and exited charge energy states. Effective capacitance parameters are established and parametric approach for calculating electron levels in the molecule energy spectra is proposed. Finally transport characteristics of the molecular single-electron transistor are calculated by Monte-Carlo simulation.

Key words: molecular electronics, single-electron transistor, electronic nanodevices, discrete energy spectra, stability diagram.

 

Введение

Электронные устройства на основе наномасштабных молекулярных объектов представляют интерес по многим причинам. Кроме очевидного увеличения пространственной плотности элементов, надо иметь в виду потенциальную возможность использования квантовых эффектов, отсутствующих в классических электронных устройствах и позволяющих надеяться на создание новых способов обработки и передачи информации [1].

Во избежание путаницы в терминологии уточним понятие «молекулы», являющейся составным функциональным элементом таких устройств и используемое нами в данной статье. Дело в том, что внешние электромагнитные поля и транспорт электронов приводят как к изменению полного электрического заряда молекулы, так и к изменению пространственного расположения атомов, входящих в её состав. Молекула в процессе переноса может переходить от одного изомера к другому, что соответствует переходу между локальными минимумами полной энергии, связанными с определенной пространственной конфигурацией атомов. Поэтому в данной работе «молекулой» будем называть устойчивую совокупность атомов с зарядами ядер , локализованых в некоторой области пространства и образующих единый односвязный объект.

Для теоретического изучения электронного переноса будем рассматривать электрические контакты типа «молекула-электрод», наиболее важные с точки зрения практического применения. При этом можно выделить два предельных случая, существенно влияющих на способ теоретического описания молекулярного электронного устройства.

Во-первых, это контакт, в котором между атомами молекулы и другого элемента устройства (электрод, подложка), образуются сильные химические связи (ковалентная или ионная), требующие учета обменного взаимодействия электронов и квантовых флуктуаций полного заряда молекулы. Если величина квантовых флуктуаций электронного заряда молекулы порядка или больше заряда электрона , то в этом случае можно говорить лишь о среднем значении полного заряда молекулы. Таким образом, полноценное теоретическое описание молекулярного устройства, в котором молекулы взаимодействуют с другими элементами через переходы с сильной связью, возможно только при рассмотрении устройства в целом как единой квантовой системы. В данной работе такие системы не рассматриваются.

Во-вторых, это контакты между молекулой и другими элементами устройства с очень малой проводимостью (так называемый одноэлектронный предел). В этом случае:

между атомами молекулы и другого элемента устройства сильных связей не образуется и возникает энергетический барьер;

ток переносится только при туннелировании электронов;

обменное взаимодействие между молекулой и другими элементами устройства пренебрежимо мало;

электроны в процессе туннельного транспорта могут рассматриваться как локализованые “на молекуле”, а величина квантовых флуктуаций электронного заряда молекулы много меньше заряда электрона .

В этом случае из соотношения неопределенностей

                    или  ,                       (1)

 

 где  - характерное значение кулоновской энергии контакта, C - его характерная емкость,  - характерное время между актами туннелирования электронов на молекулу и с молекулы,  - туннельная проводимость контакта,  - постоянная Планка,  - квантовая единица проводимости.

Для молекулы, электрический контакт которой с другими элементами удовлетворяет условию (1), можно определить зарядовое состояние как

                                                                                      (2)

 

где  - полное число электронов в молекуле,  - заряды ядер. При этом влияние туннельного переноса электронов между электродами и молекулой можно рассматривать как малую поправку, что позволяет использовать для расчетов собственные волновые функции изолированной молекулы.

Одноэлектронный туннельный транзистор с уединенной молекулой  в качестве центрального острова [2] относится как раз к обсуждаемым наномасштабным электронным устройствам. Его работа основывается на явлении коррелированного туннелирования электронов в системах с малой емкостью [3,4], наблюдаемом при выполнении соотношения (1) и при условии малости энергии температурных флуктуаций по сравнению с характерной кулоновской энергией контакта E_С:

                                      ,                                          (3)

 

где k_B – постоянная Больцмана. При этом отличительной чертой устройств молекулярной одноэлектроники в силу их малости является дискретность энергетического электронного спектра центрального острова - молекулы (расстояние между уровнями ~ 0.1 – 1 эВ) [5]. Плотность и структура электронного энергетического спектра используемой молекулы влияют на процесс протекания тока, определяя тем самым особенности транспортных характеристик (ВАХ и сигнальных характеристик) молекулярного одноэлектронного транзистора. Подробное изучение электронных спектров (электронных и спектров полной энергии) конкретных молекул для различных зарядовых состояний и механизмов транспорта через отдельно взятые электронные энергетические уровни поможет объяснить особенности транспортных характеристик одноэлектронных транзисторов, созданных на их основе, и связать эти особенности с параметрами молекул.

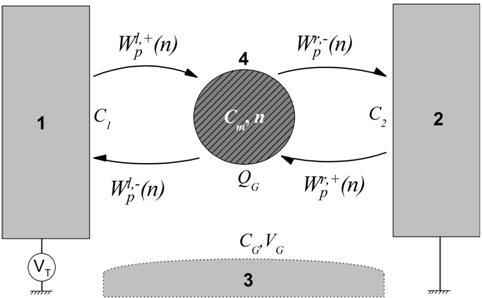
Модель молекулярного одноэлектронного транзистора, рассматриваемая в работе, схематично показана на Рисунке 1. Молекулярный одноэлектронный транзистор состоит из двух массивных электродов и молекулярного острова, образующих в цепи протекания тока два последовательных туннельных перехода [3]. Изменяя электрический потенциал затвора транзистора V_G, можно управлять его туннельным током I_T.

 

Рис.1.  Схема возможных туннельных событий между электродами и молекулой в молекулярном одноэлектронном транзисторе. 1 – левый электрод, 2 – правый электрод, 3 – управляющий электрод, 4 – молекула. Здесь ,   – темпы туннелирования электронов с левого (правого) электрода на молекулу и в обратном направлении, V_T – приложенное туннельное напряжение транзистора, Q_G – наводимый на молекуле заряд, характеризующий воздействие управляющего потенциала V_G через нетуннельную емкость C_G.

 

Практическое применение молекулярных одноэлектронных устройств основывается на использовании зарядовых эффектов - кулоновской блокады и модуляции туннельного тока [1], которые могут возникать в них при условии малости тепловых флуктуаций (3). Из этого условия  получаем, что для работы при комнатной температуре характерная емкость C [6] молекулярного острова должна быть менее  Ф, что соответствует характерным размерам устройства в несколько единиц нанометров. Экспериментальное изготовление структуры столь малого размера является сложной и ресурсоемкой технической задачей [7], поэтому поиск оптимальной молекулы для центрального острова молекулярного одноэлектронного транзистора весьма актуален.

Изучение влияния структуры электронных спектров молекул на транспортные характеристики молекулярного одноэлектронного транзистора на их основе позволит в дальнейшем осуществлять целенаправленный подбор молекул для создания транзисторов с требуемыми характеристиками.  Для этого желательно сформулировать ряд устойчивых критериев, позволяющих связать электронные спектры молекул с особенностями на ВАХ и сигнальных характеристиках, и тем самым классифицировать используемые молекулы в плане пригодности для получения желаемых транспортных характеристик.

В представленной работе для решения такой задачи на первом этапе производился  квантовый расчет энергетических спектров выбранных молекул. Данные расчетов позволяют определить главные параметры, необходимые для последующего моделирования электронного транспорта через одноэлектронный транзистор на основе одной из молекул. К таким параметрам относятся одночастичные электронные уровни в молекуле, через которые идет транспорт, а также емкостные характеристики молекулы. На основе рассчитанных данных для выбранных молекул производилось имитационное моделирование транспортных характеристик молекулярного одноэлектронного транзистора на базе этих молекул.

 

1.     Электронные энергетические спектры молекул

1.1  Расчет энергетических спектров молекул

Поскольку основной целью данной работы является изучение влияния дискретного энергетического спектра в реальных молекулах на транспортные характеристики молекулярного одноэлектронного транзистора, необходимо уточнить, о каком энергетическом спектре идет речь в рамках нашей модели (см. (1)). Представим полный гамильтониан молекулярного одноэлектронного транзистора в виде:

                    ,                           

где  – гамильтониан молекулы, , – части, соответствующие левому, правому электродам и подложке,  – слагаемое, описывающее туннелирование через левый и правый контакты молекулы и электродов,  – слагаемое, описывающее энергетическую релаксацию за счет взаимодействия с подложкой.

Подложка является диэлектрической и оценка времени жизни молекулы в возбужденном состоянии (приведена ниже в разделе 2) позволяет пренебречь влиянием подложки на молекулу и воспользоваться приближением предельно медленной энергетической релаксации. При выполнении условия малости туннельной связи также будем считать влияние электродов на молекулу перенебрежимо малым (волновая функция молекулы не перекрывается с волновой функцией “берегов”).

В указанных приближениях вычисления необходимых параметров молекул [6, 8] производятся в два этапа. На первом определяется энергетически устойчивое взаимное положение атомов, что соответствует стационарному (“основному”) состоянию выбранной для моделирования молекулы. В одноэлектронном транзисторе в результате элементарного акта туннелирования молекула принимает или отдает один электрон и переходит в “возбужденные” зарядовые состояния, характеризуемые в нашей модели зарядом Q (в атомной системе единиц совпадающим с зарядовым состоянием n, определенным соотношением (2)) и мультиплетностью M[1].

Для изолированной молекулы решение уравнения Шредингера с гамильтонианом =  позволяет определить набор разрешенных энергетических состояний. Стационарные состояния молекулы являются решениями уравнения Шредингера:

                                                                   

где  - полная энергия молекулярного объекта,  - полная волновая функция молекулы (зависящая от пространственных и спиновых координат ядер и электронов), и  - совокупность всех координат ядер и электронов, соответственно. В адиабатическом приближении ядра можно считать пространственно неподвижными, и возможно разделение ядерных и электронных координат. Это позволяет разделить и волновую функцию молекулы на ядерную и электронные части и рассматривать полную энергию молекулы  как функцию ядерных координат и зарядового числа n (числа дополнительных электронов на молекуле). Локальные минимумы функции  при этом соответствуют различным изомерам молекулы (в данной работе мы пока оставляем за скобками вопрос о времени, необходимом для структурной перестройки молекулы, и времени нахождения на ней туннельного электрона).

Квантовый расчет энергетических спектров молекулы, соответствующих данным состояниям (для всего интересующего нас набора энергетических состояний), проводился стандартными методами при помощи программного пакета Firefly QC [9]. Устойчивая геометрия молекулы ищется последовательными итерациями, начальными данными для которых являются ее электрический полный заряд Q (или зарядовое состояние n), спиновая мультиплетность M (остающиеся неизменными) и координаты атомов, варьируемые от итерации к итерации. При этом необходимость прямого задания не только координат атомов и заряда молекулы, но и параметра M является внутренним требованием программы [9], поэтому здесь и далее мы также будем использовать этот параметр в описании состояний молекул.  

Расчет для различных значений параметра M позволил нам исследовать помимо основных также и часть возбужденных состояний молекул. В данной работе под термином “основные” понимаются состояния, обладающие минимальной полной энергией при фиксированном заряде Q, расширив таким образом понятие основного незаряженного (Q=0) состояния и на другие Q. Под “возбужденными” же понимаются состояния с мультиплетностью M отличной от минимально возможной при заданном заряде Q.

Среди методов квантового расчета энергетических спектров молекулы наиболее подходящим для нашей модели является метод Хартри-Фока [10] самосогласованного поля. Методом Хартри-Фока были рассчитаны “основные” состояния молекул  карборана и фуллерена в зависимости от их зарядовых состояний n.

На втором этапе для расчета “возбужденных” зарядовых состояний потребовался более точный метод Меллера-Плессета 2-го порядка, учитывающий коррелированность движения электронов [10]. В ходе квантово-механических вычислений использовался базис гауссовских волновых функций G 6-311 (с включением диффузных функций для сильно заряженных состояний).

 

1.2 Результаты расчета электронных энергетических спектров

           В данной работе изучались спектры популярных в экспериментальных и теоретических исследованиях  молекулы  карборана C₂B₁₀H₁₂ и фуллерена C₆₀ [11-14], состоящих из достаточно малого количества атомов, обладающих симметрией близкой к сферической и структурно устойчивых к изменению заряда. Для того, чтобы детально изучить процесс туннелирования электронов через молекулу, рассмотрим структуру энергетических одночастичных электронных уровней молекулы карборана C₂B₁₀H₁₂ в области щели HOMO-LUMO^[2].

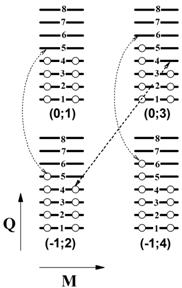
На Рис.2а  достаточно сложная картина рассчитанного электронного энергетического спектра молекулы модельно проиллюстрирована упрощенной схемой. На ней представлено четыре из возможных состояний молекулы, как восьми-уровневой системы, и указаны уровни в спектре, которые электрон занимает или покидает при изменении заряда. На каждом уровне может находиться по 2 электрона с противоположными спинами. Состояния с не минимальным M при равных зарядах Q являются “возбужденными”. Так состояние (Q;M) = (0;1) соответствует электрически нейтральному “основному” зарядовому состоянию молекулы.

 

                  

   (а)                                                                                  (б)

                                                                                                                                    

Рис.2. (а) Схема переходов восьми-уровневой системы одноэлектронного энергетического спектра.  Белая точка обозначает электрон, занимающий электронный уровень. Стрелки показывают разрешенные пути эволюции системы и указывают на энергетический уровень, участвующий в этом. Состояние системы определяется парой чисел (Q;M). Здесь Q – полный электрический заряд молекулы, M – спиновая мультиплетность молекулы.

(б) Диаграмма возможных путей перехода молекулы из одного энергетического состояния в другое для одноэлектронного энергетического спектра карборана молекулы карборана C₂B₁₀H₁₂. Черным и серым отмечены занятые и вакантные энергетические уровни, соответственно, две колонки уровней означают электронные уровни со спинами «вверх» и «вниз». E_i – энергия i-го электронного уровня,   – величина энергетической щели молекулярного электронного спектра. Стрелки соответствуют стрелкам на Рис.2а.

 

Пунктирными стрелками указаны варианты перехода молекулы из одного разрешенного состояния в другое. Учет вероятностей всех таких возможных переходов позволил нам далее смоделировать процесс электронного туннельного транспорта в одноэлектронном транзисторе с прямым заданием энергетических уровней электронов, участвующих в транспорте.

Анализ показывает, что основной вклад в электронный транспорт при , дают уровни вблизи энергетической щели HOMO-LUMO. Точный расчет дает более сложную картину одночастичного (электронного) энергетического спектра молекулы (в отличие от представленной упрощенной диаграммы): при изменении зарядового состояния n и мультиплетности M меняется также и положение энергетических уровней друг относительно друга.

На Рис.2б показан участок квантовым образом рассчитанного энергетического спектра в области щели HOMO-LUMO для тех же четырех состояний, что и на Рис.2а, и так же указаны возможные направления изменения состояния системы. Каждая ячейка – это отдельная пара значений (Q;M). Пунктирными стрелками соединены электронные уровни энергетического спектра с одинаковыми номерами, но в различных зарядовых состояниях молекулы. Именно эти уровни отвечают за соответствующее изменение зарядового состояния, и именно через них осуществляется транспорт электронов в молекуле.

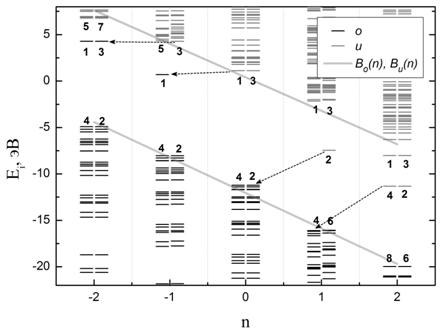
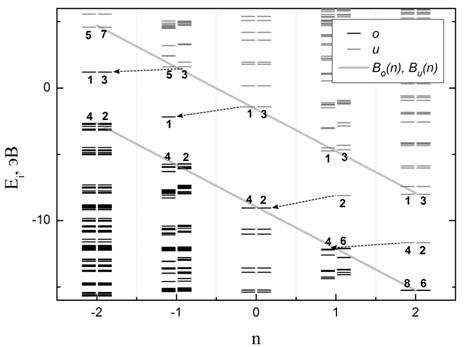
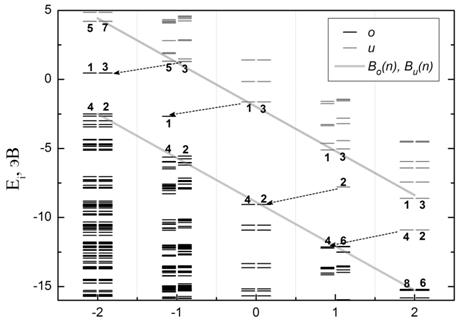
На Рис.3а представлена диаграмма энергетического спектра одночастичных уровней невозбужденных состояний в зависимости от зарядового состояния n для молекулы карборана. Расчет зарядовых состояний молекулы произведен без учета изменения ее геометрии  (межатомных расстояний в молекуле).

 

1.3  Особенности энергетического спектра молекул

Как было отмечено, при изменении заряда и (или) мультиплетности молекулы меняется положение одночастичных энергетических уровней. Однако, на Рис.2б можно видеть, что величина энергетической щели ΔE_HL при этом остается приближенно неизменной (см. также Таблицу 1). Выделенная нами энергетическая щель в общем случае отлична от HOMO-LUMO. Для карборана C₂B₁₀H₁₂ щель ΔE_HL совпадает с его щелью HOMO-LUMO только при n = 0, при остальных же значениях n величина HOMO-LUMO по определению оказывается меньше (то есть при n = 0 HOMO-LUMO максимально). Рассмотрим как меняется структура спектра с изменением заряда молекулы подробнее.

На Рис.3а, где участки энергетического спектра при различных n отложены по общей оси энергии, можно видеть, что с увеличением  или уменьшением зарядового состояния n в первоначальной энергетической щели ΔE_HL возникают энергетические уровни. Такие уровни отмечены на Рис.3а цифрами, а стрелками показано изменение положения тех вакантных уровней, которые занимает электрон при изменении n. Будем называть такие электронные уровни «дополнительными».

На сколько нам известно, появление таких уровней внутри энергетической щели молекулы ранее не описывалось и не использовалось при моделировании электронного транспорта в молекулярных одноэлектронных устройствах. Появление «дополнительных» уровней также очень похоже на появление примесных энергетических уровней в запрещенной зоне полупроводников.

Отметим, что зависимость положения электронных уровней на верхней и на нижней границах энергетической щели ΔE_HL от зарядового состояния n (Рис.3а) близка к линейной. При этом коэффициенты наклона  этих кривых (на Рис.3а B_o(n) и B_u(n)) приблизительно одинаковы, что можно рассматривать как неизменность величины энергетической щели ΔE_HL при n=-2...2 не меняется (что подтверждает наблюдение, отмеченное на Рис. 2б). По нашим оценкам положение «дополнительных» уровней в энергетической щели также описывается линейной зависимостью по n. Сдвиг энергетической щели ΔE_HL при изменении n на 1 должен быть равен зарядовой энергии молекулы , где  – емкость молекулы (см. Таблицу 1). То есть, из нашего представления о емкости наклон энергетической щели спектра определяется собственной емкостью C_m молекулы.

           

           

(a)                                                                                               (б)

Рис.3. Зависимость положения электронных уровней энергетического спектра (а) невозбужденных и (б) однократно состояний возбужденных от зарядового состояния n для молекулы карборана. Буквами обозначены: o – занятные электронные уровни, u – вакантные электронные уровни, B_o(n) и B_u(n) – «нижняя» и «верхняя» границы энергетической щели спектра (сплошная серая линия).  Цифрами отмечены «дополнительные» зарядовые уровни щели, а стрелками соединены те из них, на которые приходят и с которых уходят электроны при изменении n. Расчет зарядовых состояний молекулы произведен без учета изменения ее геометрии.

 

Таблица  1. Рассчитанные значения собственной [7] С_m и взаимной [8] C₁₍₂₎  эффективной емкости молекул. Здесь E_C – Кулоновская энергия (e²/2С_m), ΔE_HL – средняя величина энергетической щели спектра («HOMO-LUMO основного незаряженного состояния»). Взаимная емкость C₁₂ приведена для расстояния между молекулой и электродом  D = 2.5 нм, D =  R₁₂ / 2.  

 

Молекула	Сm, 10-20 Ф	C1(2) , 10-21 Ф	EC, эВ	ΔEHL, эВ
C2B10H12	3.2	2.8	4.0	12.0
C60	5.2	4.9	2.5	8.9

 

 

На Рис.3б показана аналогичная зависимость положения одночастичных уровней энергетического спектра от n для однократно возбужденных (M отличается на 2 от минимальной при данном Q, что соответствует двум распаренным по спину электронам) состояний карборана без учета изменения геометрии молекулы при расчете спектров. Параметры численного анализа данных линейных зависимостей представлены в Таблице 2. Обнаружено, что величина щели  остается также неизменной и при изменении спиновой мультиплетности молекулы M, то есть для “возбужденных” состояний.

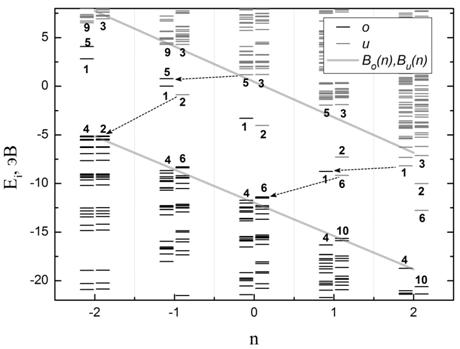
Для молекулы фуллерена C₆₀ аналогичные зависимости положения одночастичных уровней основного (невозбужденного) состояния от зарядового состояния n приведены на  Рис.4а и Рис.4б. Рис.4а – результат расчета без учета изменения структуры молекулы с изменением заряда, Рис.4б – с нахождением оптимальных межатомных расстояний. Параметры зависимостей приведены в Таблице 3.

 

Таблица  2. Параметры линейной регрессии вида  для зависимости энергии  одночастичных уровней энергетического спектра  от зарядового состояния n для молекулы карборана C₂B₁₀H₁₂ без учета изменения ее геометрии.  - ширина энергетической щели (); S_α, S_β, SΔE_HL – погрешности коэффициентов α, β и ; r –коэффициент корреляции метода наименьших квадратов.

 

Степень возбуждения	Граница щели	α, эВ	Sα, эВ	β, эВ	Sβ, эВ	r	ΔEHL, эВ	SΔEHL, эВ
0	Bo(n)	-3.8	0.2	-12.1	0,3	0.99	12.5	0.8
	Bu(n)	-3.6	0.4	0.4	0,5	0.96
1	Bo(n)	-3.4	0.1	-12.0	0,1	1.00	12.4	0.7
	Bu(n)	-3.6	0.4	0.5	0,6	0.96
2	Bo(n)	-4.0	0.2	-12.6	0,3	0.99	13.9	1.0
	Bu(n)	-3.7	0.5	1.3	0,8	0.92

 

 

(a)	(б)

                                                                                            
Рис. 4. Зависимость положения одночастичных уровней рассчитанного спектра основного (невозбужденного) состояния от зарядового состояния n для молекулы фуллерена C₆₀: (а) – без учета изменения структуры молекулы с изменением заряда, (б) – с нахождением оптимальных межатомных расстояний. Обозначения аналогичны принятым на Рис.3.

 

Таблица  3. Параметры линейной регрессии вида  для зависимости энергии  одночастичных уровней энергетического спектра  от зарядового состояния n для молекулы фуллерена C₆₀.

 

БЕЗ УЧЕТА ИЗМЕНЕНИЯ ГЕОМЕТРИИ МОЛЕКУЛЫ
Степень возбуждения	Граница щели	α, эВ	Sα, эВ	β, эВ	Sβ, эВ	r	ΔEHL, эВ	SΔEHL, эВ
0	Bo(n)	-3.15	0.03	-8.95	0.04	1.00	7.4	0.1
	Bu(n)	-3.16	0.05	-1.60	0.07	1.00
1	Bo(n)	-3.09	0.15	-8.58	0.19	0.99	7.1	0.2
	Bu(n)	-3.05	0.02	-1.49	0.02	1.00
С ОПТИМИЗАЦИЕЙ ГЕОМЕТРИИ МОЛЕКУЛЫ
0	Bo(n)	-3.20	0.04	-8.88	0.06	1.00	6.9	0.2
	Bu(n)	-3.20	0.09	-1.98	0.12	1.00

 

Учет изменения геометрии фуллерена при варьировании значения n приводит к сдвигу «дополнительных» уровней относительно их положения без оптимизации геометрии на 0.6 - 0.7 эВ, что составляет 10% от величины ширины энергетической щели . Структура спектра и появление «дополнительных» уровней в спектре фуллерена С₆₀ на Рис.4а полностью аналогичны рассмотренным для молекулы карборана на Рис.3а. Таким образом, найденные закономерности образования энергетического спектра являются общими для данных молекул.

 

1.4  Параметризация электронного спектра

Таким образом, величина щели спектра ΔE_HL, зарядовая энергия , положение нижней границы (B_o(n)) и «дополнительных» уровней в энергетической щели могут быть теми основными параметрами, которые определяют главные особенности электронного спектра молекул для наиболее важного в одноэлектронике небольшого набора зарядовых состояний n. При этом в процессе электронного транспорта интерес представляют лишь высшие заполненные уровни (HOMO) в спектре, с которых уходит электрон, низшие уровни LUMO, на которые он может протуннелировать. Значит, при моделировании транспорта достаточно знать положение таких «транспортных» уровней, а не всех уровней спектра.

Указанные соображения позволяют параметризовать положение «транспортных» уровней спектра и представить из энергию в виде линейной функции . Этот простой подход для приближенного определения наиболее значимой части энергетического спектра молекул может быть использован в качестве альтернативы непосредственному квантовому расчету большого числа энергетических спектров зарядовых состояний для громоздких молекулярных систем. Для больших молекул прямой расчет даже одного состояния (при заданных Q и M) требует порой весьма значительных вычислительных ресурсов. Таким образом, приведенная схема расчета энергии уровней энергетической щели способна помочь значительно упростить задачу моделирования транспорта через сложные молекулярные системы. Например, она была использована нами при расчете золотых наночастиц различных размеров, стабилизированных оболочкой из додекантиолов в работе [15].

Для рассматриваемых молекул точный расчет вполне доступен, поэтому в данной статье мы такой параметризацией не пользуемся, чтобы иметь на будущее “твердую базу” в виде точного положения уровней электронного спектра.

 

1.5  Определение электрической эффективной емкости молекул

Для численного расчета радиотехнических характеристик электронного транспорта в молекулярном одноэлектронном транзисторе необходимо также определить собственные и взаимные емкости молекулярного острова и туннельных переходов. Методика определения и расчета емкости наноразмерных квантовых и квазиквантовых объектов предложена нами в работах [6, 8]. Эта методика основана на использовании зависимости полной энергии молекулы от ее полного электрического заряда. Полная энергия молекулы может быть вычислена  на основе спектра одночастичных энергий молекулы как это и предполагается в приближении Хартри-Фока^[3] [10].

Использование  спектра полной энергии удобно для расчета туннельного тока через молекулу. Использование же одночастичного электронного спектра позволяет облегчить задачу изучения влияния дискретного энергетического спектра на транспортные характеристики молекулы и выявления связи положения особенностей на транспортных характеристиках с одиночными энергетическими уровнями.

Для расчета емкостей достаточно значений полной энергии для «основных» зарядовых состояний. Но в нашем случае полная энергия являлась одним из выходных значений расчетов в пакете Firefly QC. Поэтому отметим также ряд закономерностей, которые нам удалось наблюдать в спектре для всей совокупности рассмотренных состояний (в т.ч. и с не минимальными M).

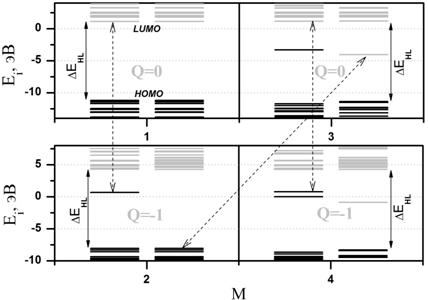
На Рис.5 представлена диаграмма значений полной энергии молекулы E_полн карборана при различных комбинациях зарядового состояния n = -2… +2 и мультиплетности M молекулы, и возможные переходы между этими состояниями, реализованные далее при моделировании электронного транспорта. Сдвиг между уровнями полной энергии соседних «возбужденных» состояний при одинаковых n составляет примерно одинаковое значение 7.5 эВ (при этом следует учитывать, что точность расчета сильно возбужденных состояний всегда ниже, чем основных зарядовых состояний). Для ряда возбужденных состояний, как отмечалось и в работах [6,8,16,17] для основных состояний, наблюдаемая зависимость от заряда близка к квадратичной, что отмечено на рисунке 5. Таким образом, возникает картина эквидистантных по энергии парабол. Данная особенность также может быть одним из возможных путей параметризации, при определении «возбужденных» энергетических состояний молекул.

 

Рис.5. Диаграмма рассчитанных значений полной энергии молекулы E_full карборана при различных зарядовых состояниях n и мультиплетности M молекулы (то есть, основных и возбужденных состояниях). Стрелками отмечены пути эволюции молекулярной системы между разрешенными состояниями (n;M) молекулы в процессе электронного транспорта. Основные состояния на диаграмме закрашены черным цветом. Серыми линиями нанесены квадратичные аппроксимации для ряда основных и возбужденных сосотяний молекулы.

 

Собственная емкость молекул C_m карборана и фуллерена, а также взаимная емкость системы «молекула-электрод» C₁₂, в случае транзистора взяты из работы [8] и приведены в Таблице 1. Данные емкостные параметры необходимы для последующего моделирования работы одноэлектронного транзистора.

 

2  Расчет транспортных характеристик транзистора

2.1  Метод имитационного моделирования и теоретическая модель

 Как было указано ранее, в настоящей работе рассматривается одноэлектронный транзистор со слабой связью  молекулы и туннельных электродов. При таком условии молекула и туннельные электроды не являются единой квантовой системой, а проводимость туннельных переходов много меньше квантовой единицы проводимости e²/h.

При описании процессов туннелирования в молекулярном одноэлектронном транзисторе мы работали в приближении одночастичных процессов. Данное приближение в нашем случае может быть использовано, поскольку в слабосвязанных системах вероятность многочастичных процессов много меньше вероятности одночастичных. В наших расчетах перенос электронов между молекулой и электродами можно рассматривать как последовательность независимых актов туннелирования.

При расчете и моделировании процессов транспорта решалась система кинетических уравнений, которая с учетом описанных выше условий в одночастичном приближении имеет вид:

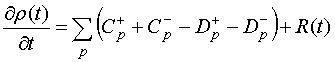                                              (4)

 

где – функция распределения вероятности электронных конфигураций,  и  – вероятности туннелирования электрона на молекулу на уровень p,  и  – вероятности туннелирования электрона с уровня p молекулы на электрод, R(t)– слагаемое, описывающее релаксацию электронов в молекуле.

Использовался общепринятый метод имитационного моделирования Монте-Карло [18] для расчета транспортных характеристик одноэлектронного транзистора с дискретным спектром центрального острова в режиме предельно медленной энергетической релаксации электронов [19]. Метод представляет собой вероятностный способ решения системы кинетических уравнений, позволяющий исследовать электронный туннельный транспорт непосредственно в динамике, описываемой уравнениями (4). В частности, одним из его преимуществ является возможность наглядного представления уровней, задействованных в туннельном транспорте в одноэлектронном транзисторе. На Рисунке 1 схематично показаны возможные типы туннельных событий в мономолекулярном одноэлектронном транзисторе: 

а) электрон покидает молекулу через левый или правый переход. Скорость такого процесса ;

б) электрон приходит на молекулу через левый или правый переход. Скорость такого процесса .

Каждый из этих процессов является результатом произведения 3-х независимых (т.к. система слабо связана) вероятностей:

 

                                                   

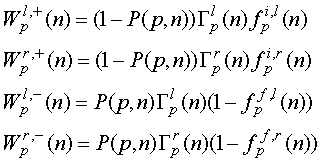
где P(p,n) – вероятность того, что уровень p занят при зарядовом состоянии молекулы n,  – вероятность туннелирования через левый (правый) переход,  – функция электронного распределения Ферми-Дирака в электродах 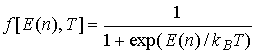, которая при подстановке энергии туннелирующих электронов (определяемой из энергетического баланса) имеет вид:

 

                                            

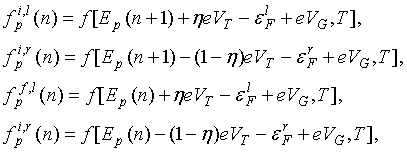
где h - коэффициент деления приложенного туннельного напряжения на молекуле, - энергия Ферми на левом (правом) электроде, E_p(n) – энергия электрона ни уровне p в спектре молекулы при зарядовом состоянии n, рассчитанная ранее в разделе 1.2. Влияние управляющего электрода здесь задано потенциалом затвора V_G (при этом Q_G = C_G V_G) и выражено сдвигом спектра на eV_G. Индекс i используется для электронов в электроде до туннелирования, а индекс f – для пустого состояния в электроде после туннелирования.

Также должен быть учтен процесс энергетической релаксации электронов в молекуле. Скорость такого процесса устанавливается релаксационным членом R(t). Оценка времени жизни молекулы в возбужденном состоянии дает τ ~ 10^-10 c [5], что позволяет в рамках нашей модели воспользоваться приближением предельно медленной энергетической релаксации τ_rel >> τ_tun ~ 10^-11 с (эти ограничения дают верхний частотный предел нашего приближения для радиофизических применений). В используемом нами приближении R(t) равно нулю.

Таким образом, процесс туннельного транспорта складывается из двух указанных выше типов событий. Молекула при этом помещена в центр зазора. После задания всех необходимых параметров при помощи моделирования методом Монте-Карло были рассчитаны транспортные характеристики мономолекулярного одноэлектронного транзистора.

 Примененный нами метод Монте-Карло имитационного моделирования основывается на марковском приближении, в соответствии с которым вероятность перехода рассматриваемой системы из текущего состояния в любое другое не зависит от истории предыдущих переходов, совершенных системой. Вычисление туннельного тока в этом случае сводится к последовательному рассмотрению различных электронных состояний, подсчету времени нахождения системы в них и расчету суммарного перенесенного заряда.  Таким образом, полный туннельный ток I_T в системе рассчитывается по формуле:

                                                                                       

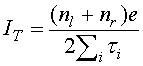
n_l – суммарное число электронов, прошедших через левый переход на молекулу, n_r – суммарное число электронов прошедших через правый переход с молекулы,  – время жизни текущего состояния молекулы (~10^-10 c).

 

2.2  Результаты моделирования транспортных характеристик

Расчет транспортных характеристик по описанной выше методике проводился для молекул карборана и фуллерена. Для карборана была использована схема переходов между квантовым образом рассчитанными состояниями молекулы, изображенная на Рисунке 5. Аналогичная схема переходов использовалась и для фуллерена, но только до однократно возбужденных состояний включительно, что объясняется уже большей вычислительной сложностью для больших значений M. Электроды в расчетах считались сделанными из золота и одинаковыми, температура принята близкой к абсолютному нулю.

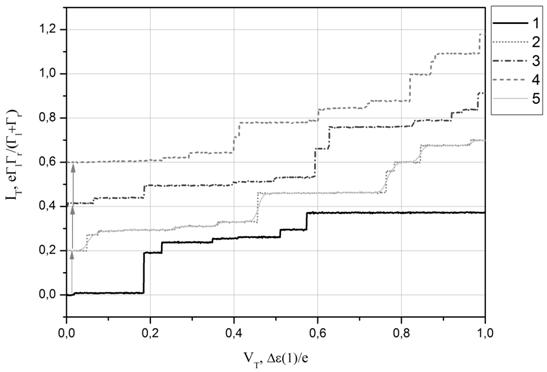
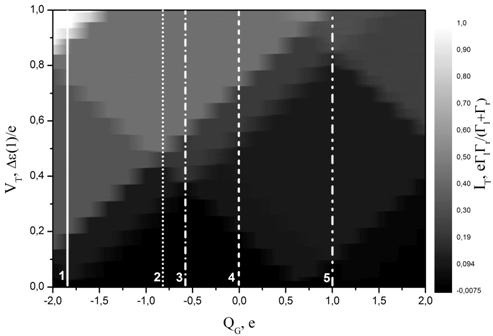
На Рис. 6а и 7а представлены контурные диаграммы одноэлектронных транзисторов на основе карборана и фуллерена^[4], полученные с использованием рассчитанных спектров этих молекул. Белыми линиями на диаграммах отмечены профили ВАХ, изображенных соответственно на Рис.6б и 7б. Для определения уровней, отвечающих за транспорт использовался следующий подход: из общего набора энергетических состояний выключалось одно состояние, после чего становилось видно, на какие ступеньки на ВАХ это влияет.  Так на Рисунке 6а для карборана для каждого выбранного управляющего напряжения указаны состояния, которые в данной конфигурации не участвуют в электронном туннельном транспорте.

 

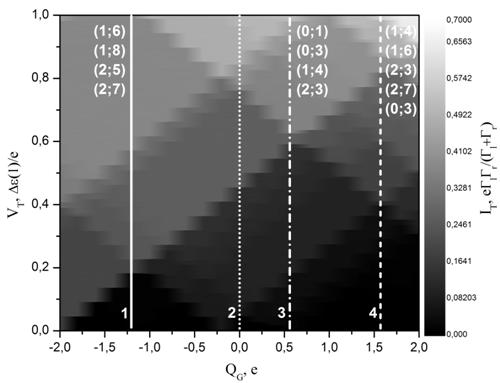
(а)                                                                                                              (б)

Рис.6. (а) Контурная диграмма, рассчитанная на основе энергетических спектров карборана C₂B₁₀H₁₂. (б) Соответствующие профили ВАХ, отмеченные на контурных диаграммах цифрами. Профили ВАХ для удобства смещены по оси туннельного тока I_T. Туннельный ток и туннельное напряжение приведены в относительных единицах ( – характерная Кулоновская энергия). ВАХ №5 – при комнатной температуре.

 

  

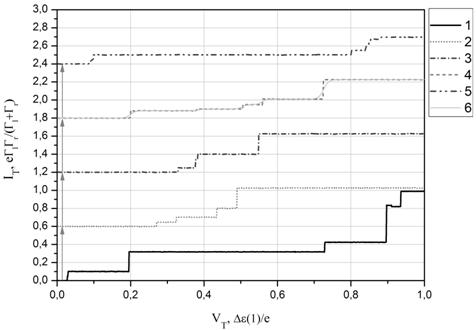
(а)                                                                                                            (б)

Рис.7. (а) Контурная диграмма, рассчитанная на основе энергетических спектров фуллерена C₆₀. (б) Соответствующие профили ВАХ, отмеченные на контурных диаграммах цифрами. Профили ВАХ для удобства смещены по оси туннельного тока I_T. Туннельный ток и туннельное напряжение приведены в относительных единицах. ВАХ №6 – при комнатной температуре.

 

2.3  Обсуждение результатов

Включение в электронный транспорт возбужденных энергетических состояний молекулы выражается появлением малых ступенек на ВАХ. При этом на примере кривой 5 на Рис.6б и кривой 6 на Рис.7б можно видеть, что при более высокой температуре данные особенности дискретного спектра изучаемых молекул на ВАХ размываются и практически не будут различимы на фоне больших ступенек.

Энергетически невыгодные возбужденные состояния выпадают из процесса электронного транспорта по мере увеличения заряда Q_G. Однако, что касается других зарядовых состояний, добавляющихся с увеличением Q_G из-за электростатического смещения спектра острова, то здесь всё не так очевидно. В зависимости от величины заряда Q_G формируются как большие, так и маленькие ступеньки на ВАХ. Включение в транспорт нового зарядового состояния n отражается на контурной диаграмме появлением нового большого Кулоновского ромба.

По результатам расчетов зарядовые состояния, связанные с приходом электронов на нейтральную молекулу, практически не участвуют в туннельном транспорте. Они являются маловероятными, поскольку добавление электрона на нейтральную молекулу сильно меняет ее структуру. Зарядовые же состояния рассматриваемых молекул n ниже -2 вообще являются энергетически нестабильными.

Наиболее полно исследована в нашей работе молекула карборана.  В работе [20] в туннельной системе «СТМ-молекулярный кластер-подложка» была получена «Кулоновская лесница» для карборановым молекулярным кластером 1,7-(H₃)₂-1,2-C₂B₁₀H₉Tl(OCOCF₃)₂. Использованная в приведенной работе молекула хоть и основана так же на карборане, но значительно отличается от промоделированной нами как по составу, так и по размеру (в 3 раза). Оценка размера экспериментально полученной Кулоновсой блокады при комнатной температуре дает примерно 50 мВ. В нашей расчетной модели для простого карборана C₂B₁₀H₁₂ мы получили Кулоновскую блокаду 90 мВ. Можно видеть, что несмотря на столь значительные структурные различия объектов, величины Кулоновской блокады оказываются сопоставимы по порядку величины и по форме полученных ВАХ.

 

Таким образом, в результате анализа рассчитанных в данной работе электронных спектров молекул удалось выделить те уровни («транспортные») в области энергетической щели, которые определяют особенности электронного транспорта через молекулу в составе одноэлектронного молекулярного устройства. В частности, выявлено возникновение «дополнительных» уровней внутри энергетической щели спектра молекул при изменении полного электрического заряда,  прежде неизвестных при моделировании молекулярных одноэлектронных устройств.

Обоснована параметризация положения «транспортных» уровней энергетического спектра молекул простой линейной функцией E_i(n). При этом характерными параметрами молекулы, определяющими ее транспортные свойства,  являются ее зарядовая энергия E_C, величина энергетической щели ΔE_HL (совпадающей с HOMO-LUMO только при отсутствии «дополнительных» уровней), положение нижнего энергетического уровня B_o(n) и «дополнительных» уровней в щели ΔE_HL. Эти параметры определяют существенные особенности молекулярных энергетических спектров для наиболее важного диапазона зарядовых состояний n.

Предложенный подход к определению энергетических спектров при различных зарядовых состояниях может быть использован для минимизации количества необходимых квантовых расчетов и при моделировании одноэлектронных устройств на основе более крупных молекулярных объектов. В частности, нами был проведен расчет для более сложного, чем рассмотренные молекулы, молекулярного кластера платины Pt₅(CO)₆(PPh₃)₄, состоящего из 153 атомов [13]. Для расчета основных состояний Pt₅(CO)₆(PPh₃)₄ был выбран базис SBKJC ECP [21], и он показал качественно те же характерные особенности электронных спектров.

Моделирование транспортных характеристик одноэлектронного транзистора на основе молекул карборана и фуллерена c использованием рассчитанных спектров этих молекул показало, что формирование туннельного тока через молекулу и особенности ВАХ одноэлектронного транзистора определяются весьма ограниченным количеством состояний молекулы, задающихся совокупностью величин зарядового состояния и спиновой мультиплетности.

Таким образом, использованные методы позволили выявить не только электронные уровни в молекулах, но и состояния самих молекул, ответственные за электронный транспорт. Остальные (такие как возбужденные) состояния вносят существенно меньший вклад в формирование туннельного тока и вид диаграмм стабильности практически не меняется.

 

3. Заключение

Выявленные в данной работе закономерности энергетических спектров молекул позволяют рассчитывать на то, что в дальнейшем при проектировании молекулярных наноустройств эти закономерности могут быть учтены не только прямым расчетом энергетических спектров реальных нанообъектов, но и с помощью предложенного нами параметрического подхода для определения этих спектров.

Такой подход может помочь значительно сократить количество квантовых расчетов, облегчить моделирование электронного транспорта в молекулярных системах, что тем самым упростит задачу целенаправленного подбора молекул для создания одноэлектронных транзисторов с требуемыми характеристиками. 

 

Благодарности

Работа выполнена при поддержке РФФИ (проекты № 12-07-00816-a, 10-07-00712-а), Федеральной Целевой Программы «Научные  и научно-педагогические кадры инновационной России» на 2009-2013 годы (проекты №14.740.11.0389, 16.740.11.0020, 14.740.11.0370) и Федеральной Целевой Программы «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы» (проект № 16.513.11.3063).

Литература

1.  Likharev, K.K. Single-electron devices and their applications. // Proceedings of the    IEEE. 1999. Vol.87. P.606.

2.  Kislov V.V., Gulyaev Yu.V. et al. //  International Journal of Nanoscience. 2004. Vol.3. P.137.

3.  Likharev, K.K. // IBM J. Res. Develop. 1988.  Vol.32. P.144.

4.  Kulik, I. O., Shekhter, R. I. //.  Sov. Phys. JETP., 4(2):308, 1975.

5.  Shorokhov V.V.,  Johansson P., Soldatov E.S. //  Journal of Applied Physics, 2002. V. 91. №5. P.3049.

6.  Шорохов В.В., Солдатов Е.С., Губин С.П., "Собственая емкость наноразмерных объектов". // РЭ. 2011.  Т.56. №3. С. 326-341.

7.  Saiful I Khondaker, Kang Luo and Zhen Yao. // Nanotechnology. 2011. V.21.  P.095204.

8.  Герасимов Я.С., Шорохов В.В., Маресов А.Г., Солдатов Е.С., Снигирев О.В., "Расчет взаимной емкости нанобъектов". // РЭ. 2011. Т.56. №12. С. 1483-1489.

9. Granovsky A. A., Firefly version 7.1.G. // [Электронный ресурс]. URL: www.http://classic.chem.msu.su/gran/firefly/index.html

10.  Минкин В. И., Симкин Б. Я., Миняев Р. М.  Теория строения молекул. М.: Высшая школа, 1979.

11.  Danilov, A. and Hedeg, V. // Nano Lett. 2008. Vol.8. №8. P.2393-2398.

12.  Park H., Park J. et al. // Nature. 2000. Vol.407. № 57.

13.  Gubin, S.P., Gulayev Yu.V. et al. //  Nanotechnology. 2002. Vol. 13. P.185-194.

14.  Soldatov  E.S. and Gubin, S. P. and Johansson, P.//  Phys. Low-Dim. Struct., 1-2:113-134, 2002.

15. Gerasimov Y.S., Shorokhov V.V., Soldatov E.S. and Snigirev O.V., “Gold nanoparticle single-electron transistor simulation”,  Micro- and Nanoelectronics – 2012, Zvenigorod, 2012.

16.  Shorokhov V.V., Soldatov E.S. and Elenskiy V.G.  //  Proc. SPIE, 7025(1):70250N, 2008.

17.  Gerasimov Y.S. // Lomonosov 2008 - Moscow State University Proceedings. 2008.

18.  Honerkamp J., “Stohastic dynamical systems: Concepts, numerical methods, data analysis.” New York: Wiley-VCH, 1994.

19.  Аверин Д.В. // ЖЭТФ. 1990. Т.97. №5. С.1661.

20.  Солдатов Е.С., Ханин В.В.  и др. // Письма в ЖЭТФ. 1996. Т.64. № 7. С.510.

21.  Walter J. Stevens, Harold Basch, and Morris Krauss // J. Chem. Phys. 1984. Vol.81, 6026. 

 

---

[1] Мультиплетность M характеризует число квантовых состояний молекулы, различающихся только ориентацией суммарного электронного спина. Состоянию с суммарным спином S=Σs_i отвечает M=2S+1, где s_i=+-1/2.

[2] HOMO-LUMO (Hightest occupied molecular orbital – Lowest unoccupied molecular orbital) – энергетическая щель между верхним заполненным и нижним вакантным энергетическими одночастичными уровнями (молекулярными орбиталями).

 

[3] Полная энергия молекулы включает в себя как сумму орбитальных энергий электронов (электронные спектры обсуждались выше), так и кулоновскую энергию электростатического отталкивания электронов, обменную энергию электронов молекулы (обусловленную учетом требования антисимметричности волновой функции)  и электростатическую энергию отталкивания положительно заряженных ядер [10].

[4]Мелкая ступенчатость изображения контурных диаграмм обусловлена не физическими эффектами, а тем, что шаг по заряду управляющего электрода Q_G составлял 0.2 e. Однако это не мешает в достаточной степени четко видеть Кулоновские ромбы.