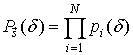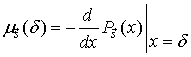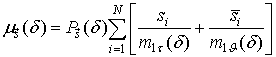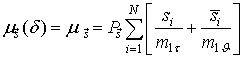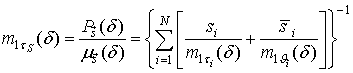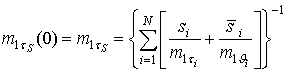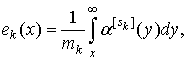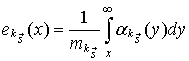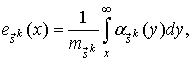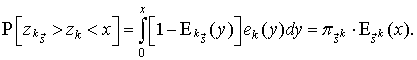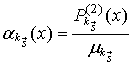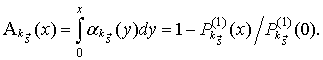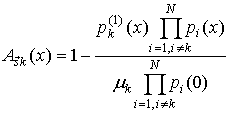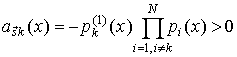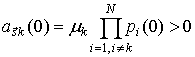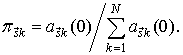УДК 621.391.14:621.396
ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ ПОЛУМАРКОВСКОЙ МОДЕЛИ СУПЕРПОЗИЦИИ
СЛУЧАЙНЫХ ПОТОКОВ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ
Ф. В. Голик
Новгородский государственный университет им. Ярослава Мудрого
Получена 29 декабря 2012 г.
Аннотация. В работе показано, что суперпозиция случайных потоков прямоугольных импульсов может быть представлена эргодической полумарковской моделью. Найдены вероятностные характеристики модели: одношаговые переходные вероятности и условная переходная функция распределения. Полученные результаты могут быть использованы при исследовании асинхронных систем передачи и обработки информации, радиолокационных систем и систем управления, а так же при анализе надежности сложных систем.
Ключевые слова. Случайный поток, полумарковский процесс, эргодическая цепь Маркова, суперпозиция потоков, переходная вероятность, условная функция распределения, радиолокация, информация, надежность.
Abstract. It is shown that the square pulse random streams superposition can be represented by an ergodic semi-Markov model.Model probabilistic characteristics are found: one-step transition probability and conditional transition distribution function. Obtained results could be applied to analysis of asynchronous communication systems, radar systems, control systems, complex systems reliability.
Keywords. Random stream, semi-Markov process, Markov ergodic chain, streams superposition, transition probability, conditional transition distribution function, radar systems, information, reliability.
Постановка задачи. Условия и ограничения
Рассмотрим систему,
состоящую из ![]() элементов, каждый из которых
может находиться в одном из двух состояний {0; 1}. Пусть состояния
элементов, каждый из которых
может находиться в одном из двух состояний {0; 1}. Пусть состояния ![]() -го элемента описывается случайным потоком
прямоугольных импульсов
-го элемента описывается случайным потоком
прямоугольных импульсов ![]() .
.
Представим
суперпозицию потоков ![]() вектором, компонентами которого являются парциальные
потоки
вектором, компонентами которого являются парциальные
потоки ![]() :
:
![]() ,
, ![]()
Процесс
![]() находится в момент
находится в момент ![]() в
в ![]() -состоянии,
если
-состоянии,
если ![]() ,
, ![]() . Во времени эти состояния описываются потоком
. Во времени эти состояния описываются потоком ![]() -состояний
-состояний
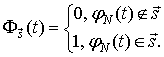
Поток
![]() может быть представлен произведением
соответствующих комбинаций парциальных потоков
может быть представлен произведением
соответствующих комбинаций парциальных потоков ![]() и их инверсий
и их инверсий ![]() [1]:
[1]:
где ![]() .
.
Соотношение (1)
справедливо для любых типов парциальных потоков, в том числе и зависимых. Однако
в настоящей работе введены ограничения на свойства потоков ![]() , а именно полагаем что:
, а именно полагаем что:
1) потоки
стационарны, т.е. законы распределения длительностей импульсов ![]() и пауз
и пауз ![]() не зависят от
не зависят от ![]() ;
;
2) существуют и
заданы плотности распределения вероятностей длительностей импульсов ![]() и длительностей пауз
и длительностей пауз ![]()
![]() ;
;
3) импульсы,
принадлежащие одному и тому же потоку, не перекрываются сами с собой, т.е.
функция распределения длительности пауз ![]() не имеет скачка при
не имеет скачка при ![]() :
:
4) аналогичному
условию удовлетворяет функция распределения ![]() длительности импульсов:
длительности импульсов:
5) существуют
математические ожидания длительностей импульсов ![]() и пауз
и пауз ![]() ;
;
6) потоки ![]() взаимно независимы в совокупности.
взаимно независимы в совокупности.
Каждому состоянию ![]() можно приписать некоторое значение
можно приписать некоторое значение ![]() . Тогда многомерному потоку
. Тогда многомерному потоку ![]() соответствует процесс
соответствует процесс ![]() ,
имеющий, например, смысл эффективности функционирования системы.
,
имеющий, например, смысл эффективности функционирования системы.
Процессы ![]() и
и ![]() относятся к классу полумарковских. Действительно, переходы
из фазовых состояний описываются эргодической цепью Маркова,
поскольку интуитивно ясно[1], что цепь возвратна и средние
времена возвращений конечны [2], а распределения времени пребывания
системы в фиксированном состоянии в общем случае отличается от
экспоненциального.
относятся к классу полумарковских. Действительно, переходы
из фазовых состояний описываются эргодической цепью Маркова,
поскольку интуитивно ясно[1], что цепь возвратна и средние
времена возвращений конечны [2], а распределения времени пребывания
системы в фиксированном состоянии в общем случае отличается от
экспоненциального.
Полумарковский процесс задан, если известны вероятности переходов и условные распределения длительности пребывания процесса в фиксированном состоянии.
Настоящая работа
посвящена определению этих характеристик для процессов, описываемых
суперпозицией ![]() случайных потоков прямоугольных
импульсов.
случайных потоков прямоугольных
импульсов.
Характеристики потока 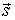 -состояний
-состояний
Прежде чем перейти к
определению вероятностных характеристик полумарковского процесса, найдем
характеристики потока ![]() ,
заданного соотношением (1).
,
заданного соотношением (1).
Отметим, что
характеристики парциальных потоков получены Н. М. Седякиным [3]. В этом параграфе мы лишь обобщим известные результаты применительно
к потокам ![]() -состояний.
-состояний.
Учитывая
независимость потоков ![]() и свойства потоков
и свойства потоков ![]() , вероятность
, вероятность ![]() того, что произвольный момент времени
того, что произвольный момент времени ![]() окажется в пределах основания укороченного на величину
окажется в пределах основания укороченного на величину ![]() импульса потока
импульса потока ![]() равна:
равна:
где 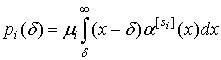 ,
вероятность попадания произвольного момента времени
,
вероятность попадания произвольного момента времени ![]() на
основание укороченного на величину
на
основание укороченного на величину ![]() импульса (
импульса (![]() ) или паузы (
) или паузы (![]() ) парциального потока
) парциального потока ![]() ;
;
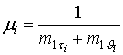 - средняя частота следования
импульсов потока
- средняя частота следования
импульсов потока ![]() ;
;
![]() -
плотность распределения импульсов (
-
плотность распределения импульсов (![]() ) и пауз (
) и пауз (![]() ) потока
) потока ![]() ;
;
Средняя частота
следования импульсов потока ![]() , укороченных
на
, укороченных
на ![]() равна :
равна :
или после преобразований
При ![]()
где
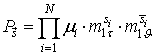 ; (8)
; (8)
Средняя длительность
![]() импульсов потока
импульсов потока ![]() , укороченных на величину
, укороченных на величину ![]() :
:
при ![]()
Плотность
распределения длительности импульса потока ![]() ;
;
![]() .
(11)
.
(11)
Таким образом все
основные характеристики потока ![]() -состояний
определяются через соответствующие характеристики парциальных потоков
-состояний
определяются через соответствующие характеристики парциальных потоков ![]() .
.
Условная переходная функция распределения
Определим функцию
распределения ![]() времени пребывания процесса
времени пребывания процесса ![]() в
в ![]() -состоянии при условии, что выход
из
-состоянии при условии, что выход
из ![]() -состояния обусловлен переходом,
возникающим в
-состояния обусловлен переходом,
возникающим в ![]() -ом парциальном потоке
-ом парциальном потоке ![]() .
.
Пусть вектор ![]() фиксирует некоторое состояние процесса
фиксирует некоторое состояние процесса ![]() . Вектор
. Вектор ![]() задает состояние, смежное с
задает состояние, смежное с ![]() -состоянием по
-состоянием по ![]() -ой компоненте. Тогда индексы
-ой компоненте. Тогда индексы ![]() означают переход из
означают переход из ![]() -состояния в состояние
-состояния в состояние ![]() .
.
Обозначим ![]() вектор, не содержащий
вектор, не содержащий ![]() -ой компоненты, т.е.
-ой компоненты, т.е. ![]() .
.
Пусть ![]() - случайный момент времени, равномерно распределенный на полуинтервале
- случайный момент времени, равномерно распределенный на полуинтервале
![]() .
.
Введем случайные величины:
![]() - длина интервала, отсчитанного от точки
- длина интервала, отсчитанного от точки ![]() до ближайшего справа скачка в потоке
до ближайшего справа скачка в потоке ![]() (недоскок процесса
(недоскок процесса ![]() );
);
![]() - длина интервала, отсчитанного
от
- длина интервала, отсчитанного
от ![]() до ближайшего справа скачка суперпозиции
потоков
до ближайшего справа скачка суперпозиции
потоков ![]() или недоскок указанного
процесса;
или недоскок указанного
процесса;
![]() - недоскок процесса
- недоскок процесса ![]() при условии перехода из состояния
при условии перехода из состояния ![]() в состояние
в состояние ![]() .
.
В соответствии с формулой Пальма запишем выражения для плотностей распределения вероятностей введенных величин:
- плотность
распределения недоскока ![]() :
:
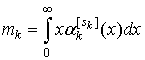 .
.
- плотность
распределения недоскока ![]() :
:
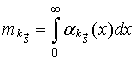
где ![]() - плотность распределения времени пребывания процесса
- плотность распределения времени пребывания процесса ![]() в состоянии
в состоянии ![]() ;
;
- плотность распределения
недоскока ![]() :
:
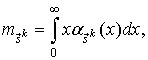
где ![]() - плотность распределения времени пребывания процесса
- плотность распределения времени пребывания процесса ![]() в
в ![]() -состоянии, при условии последующего перехода в смежное состояние
-состоянии, при условии последующего перехода в смежное состояние
![]() .
.
Определим вероятность одновременного выполнения неравенств:
![]() .
.
Вследствие
независимости величин ![]() и
и ![]() получим
получим
Здесь

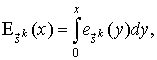
![]() -
одношаговая вероятность перехода из состояния
-
одношаговая вероятность перехода из состояния ![]() в состояние
в состояние ![]() .
.
После дифференцирования обеих частей уравнения (15) с учетом выражения (12) получим
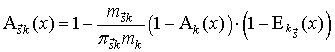 . (16)
. (16)
Здесь
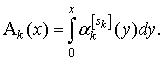
Из условий (2) и (3) следует, что ![]() Поэтому
Поэтому
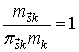
Тогда формулу (16) можно переписать в следующем виде:
![]() , (17)
, (17)
где
![]()
![]() .
.
Найдем функцию
распределения ![]() :
:

Обозначив  , получим
, получим
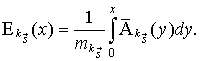
Плотность
распределения ![]() времени пребывания процесса
времени пребывания процесса ![]() в состоянии
в состоянии ![]() равна плотности распределения длительности импульсов потока
совпадения, заданного вектором
равна плотности распределения длительности импульсов потока
совпадения, заданного вектором ![]() . Согласно соотношению (11) плотность
. Согласно соотношению (11) плотность ![]() равна:
равна:
Здесь


![]()
Тогда ![]() и
и
Следовательно
 . (20)
. (20)
Математическое
ожидание ![]() времени пребывания процесса
времени пребывания процесса ![]() в
в ![]() -состоянии равно средней длительности
-состоянии равно средней длительности ![]() импульса совпадения, которую можно найти
по формуле (9)
при
импульса совпадения, которую можно найти
по формуле (9)
при ![]() :
:
![]()
Подставив выражение
для ![]() в формулу (20), получим:
в формулу (20), получим:
Выразим функцию распределения
![]() через вероятность
через вероятность ![]() , определяемую выражением
(4). Для этого по
аналогии с (18)
запишем
, определяемую выражением
(4). Для этого по
аналогии с (18)
запишем
![]()
![]()
![]()
Тогда
Подставив выражения (21) и (22) в (17) получим формулу для искомой условной переходной функции распределения
Обозначим
Учитывая, что ![]() , получим
, получим
и окончательно
Одношаговые переходные вероятности
Найдем вероятность
перехода процесса ![]() за один шаг из состояния
за один шаг из состояния ![]() в смежное по
в смежное по ![]() -ой компоненте состояние
-ой компоненте состояние ![]() . Знание этих вероятностей достаточно для определения
матрицы переходных вероятностей, поскольку вероятности переходов в несмежные
состояния, отличающиеся более чем одной компонентой, равны нулю. Это следует из
условия ординарности суммарного потока точек, образованного моментами появления
импульсов парциальных потоков.
. Знание этих вероятностей достаточно для определения
матрицы переходных вероятностей, поскольку вероятности переходов в несмежные
состояния, отличающиеся более чем одной компонентой, равны нулю. Это следует из
условия ординарности суммарного потока точек, образованного моментами появления
импульсов парциальных потоков.
Прежде чем перейти к
определению вероятности ![]() , найдем функцию
распределения
, найдем функцию
распределения ![]() времени пребывания процесса
времени пребывания процесса ![]() в состоянии, фиксируемом
вектором
в состоянии, фиксируемом
вектором ![]() . По аналогии с выражением (19) запишем:
. По аналогии с выражением (19) запишем:
Здесь
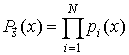 .
.
Найдем производную
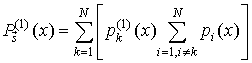 ,
,
или, с учетом (24)
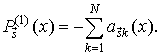
Очевидно, что
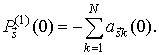
Тогда
 (26а)
(26а)
Теорема. Одношаговая вероятность перехода процесса ![]() из
состояния
из
состояния ![]() в
смежное состояние
в
смежное состояние ![]() равна
равна
Для доказательства покажем допустимость и единственность представления переходных вероятностей соотношением (27).
Функция распределения
![]() времени пребывания процесса
времени пребывания процесса ![]() в
в ![]() -состоянии может быть выражена через условные переходные функции
распределения
-состоянии может быть выражена через условные переходные функции
распределения![]() :
:
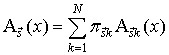 . (28)
. (28)
Подставив формулы (27) и (23а) в (28), убеждаемся, что выражение (28) тождественно равно (26а). Тем самым доказана допустимость представления переходных вероятностей соотношением (27).
Докажем, что
выражение (27) задает вероятность ![]() единственным образом. Допустим, что это
не так и существуют вероятности
единственным образом. Допустим, что это
не так и существуют вероятности ![]() , обеспечивающие выполнение равенства
, обеспечивающие выполнение равенства
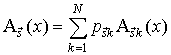 . (29)
. (29)
Предположим, что ![]() . Вычитая (29) из (28), получим
. Вычитая (29) из (28), получим
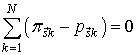
Запишем систему уравнений
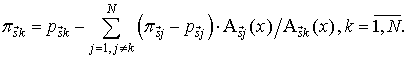
Величины ![]() не зависят от переменной
не зависят от переменной ![]() . Следовательно
. Следовательно
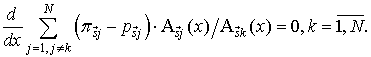 (30)
(30)
Обозначим
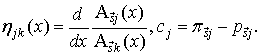
Тогда систему (30) можно привести к виду
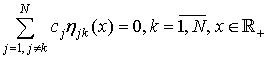 (31)
(31)
или в матричной форме
![]() (32)
(32)
Известно, что
однородная система линейных уравнений имеет тривиальное решение ![]() . Для того, чтобы система имела нетривиальное решение,
необходима и достаточно, чтобы ее определитель был тождественно равен нулю. Но
элементы определителя - функции переменной
. Для того, чтобы система имела нетривиальное решение,
необходима и достаточно, чтобы ее определитель был тождественно равен нулю. Но
элементы определителя - функции переменной ![]() . Равенство определителя нулю может выполняться лишь случайным
образом при некоторых
. Равенство определителя нулю может выполняться лишь случайным
образом при некоторых ![]() из полуинтервала
из полуинтервала ![]() . Поэтому можно считать, что система (32) имеет
гарантированное тривиальное решение и
. Поэтому можно считать, что система (32) имеет
гарантированное тривиальное решение и
![]()
Тем самым доказана единственность
переходных вероятностей ![]() и теорема в
целом.
и теорема в
целом.
Заметим, что согласно (24) и (25) ![]() и переходные вероятности (27) гарантировано
ненулевые. Следовательно, цепь Маркова эргодическая, что подтверждает сделанные
ранее предположения.
и переходные вероятности (27) гарантировано
ненулевые. Следовательно, цепь Маркова эргодическая, что подтверждает сделанные
ранее предположения.
1. Голик Ф. В. Вопросы теории случайных многомерных импульсных потоков. // Труды Второй Международной научно-технической конференции «Актуальные проблемы фундаментальных наук». Том 1, часть 2 «Техносфера». М. 1994.
2. Сильвестров Д. С. Полумарковские процессы с дискретным множеством состояний (основы расчета функциональных и надежностных характеристик стохастических систем). М.: Сов. радио, 1980.- 272 с.
3. Седякин Н.М. Элементы теории случайных импульсных потоков. М.: Сов. радио, -1965.