ДЕТЕКТИРОВАНИЕ РЕЗОНАНСНЫХ КРУТИЛЬНЫХ КОЛЕБАНИЙ КВАЗИОДНОМЕРНОГО ПРОВОДНИКА TaS₃ МЕТОДОМ ГЕТЕРОДИННОГО СМЕШЕНИЯ

 

М. В. Никитин, В. Я. Покровский, С. Г. Зыбцев

Институт радиотехники и электроники им. В.А. Котельникова РАН

 

Получена 11 февраля 2013 г., после доработки – 19 февраля 2013 г.

 

Аннотация. Предложен способ детектирования резонансных крутильных колебаний вискеров ромбического TaS₃, – квазиодномерного проводника с волной зарядовой плотности (ВЗП) – с использованием частотной модуляции напряжения на образце. При этом крутильные колебания индуцируются внутренним закручивающим моментом, возникающим в образце в электрическом поле, а модуляция проводимости вызвана крутильной деформацией образца, что принципиально отличает методику от известных ранее. Методика перспективна для исследования высокочастотных электромеханических свойств квазиодномерных проводников, в том числе, наноразмерных.

Ключевые слова: волна зарядовой плотности, кручение, наномеханика, МЭМС-НЭМС, актюатор, самодетектирование, тензосопротивление, гетеродин, модули упругости.

Abstract. Proposed is the technique for detection of torsional oscillations of whiskers of orthorhombic TaS₃ – a quasi one-dimensional conductor with charge-density wave (CDW). The technique is based on the frequency modulation of the voltage applied across the sample. The torsional oscillations are induced by the intrinsic torque arising in the CDW sample under electric field, and the conductivity modulation is induced by the torsional strain of the sample. In this the technique is essentially different from those applied before. It is promising for studies of the high-frequency electromechanical properties of the CDW conductors, including nanosized samples.

Keywords: charge-density wave, torsional strain, nanomechanics, MEMS-NEMS, actuator, self-detection, tensoresistance, heterodyne, elastic moduli.

 

Одно из актуальных направлений наномеханики – возбуждение и детектирование высокочастотных колебаний нанопроволок. В резонансных режимах такие структуры могут быть использованы в качестве весов, способных взвешивать отдельные молекулы [1]. Кроме того, предельная миниатюризация подобных устройств даёт возможность приблизиться к наблюдению квантовых состояний осциллятора [2]. Нанопроволока, как правило, закрепляется вблизи электрода – аналога затвора в транзисторе. При подаче переменного напряжения между затвором и проволокой электростатическая сила вызывает её колебания.

Непростой задачей является детектирование подобных колебаний. Применение оптических методик ограничивает размеры структур снизу [3] либо требуют монтажа зеркал [4], что усложняет конструкцию и приводит к снижению резонансных частот. В некоторых случаях образцы помещались внутрь просвечивающего электронного микроскопа, что позволяло наблюдать резонансные моды по размытию изображения [5]. Кроме очевидной сложности методики, её недостатком является разрушающее действие электронного луча [6]. В [1] для детектирования резонансных колебаний использовались уникальные автоэмиссионные свойства углеродных нанотрубок.

Важным шагом в исследовании колебаний нанообъектов стала методика [7] – гетеродинирование с частотной модуляцией (ГЧМ). Как и в большинстве экспериментов, проводящая нить подвешивается над затвором, на который подано постоянное смещение. ВЧ напряжение, возбуждающее изгибные колебания, прикладывается только к одному концу образца («истоку»), в то время как второй конец («сток») заземлён. Образец и затвор образуют конденсаторную структуру, и колебания образца вызывают изменение индуцированного на нём заряда. При совпадении частоты напряжения с частотой изгибного резонанса резко усиливается модуляция проводимости образца. Ток через образец равен произведению напряжения исток-сток и проводимости образца. Поскольку оба множителя содержат переменный сигнал одной частоты, в токе должна возникнуть постоянная компонента, пропорциональная амплитуде модуляции проводимости. При резонансе эта компонента возрастает. Чтобы её выделить, применяется частотная модуляция ВЧ сигнала, что позволяет измерить производную этой компоненты по частоте с помощью синхронного детектора (СД). Если построить показания СД в зависимости от частоты ВЧ сигнала, в резонансе можно наблюдать особенность. Подробно техника ГЧМ описана в работе [8] и диссертации В. Сазоновой [9].

Недавно методика [7] была использована для исследования упругих свойств квазиодномерного проводника с волной зарядовой плотности (ВЗП) NbSe₃ [10], обнаружена высокочастотная аномалия. Вообще говоря, механические свойства квазиодномерных проводников с ВЗП [11] отражают уникальную природу этого коллективного электронного состояния [12]. ВЗП, которую можно рассматривать как электронный кристалл внутри образца, может деформироваться в электрическом поле выше порогового, E_t. Было обнаружено, что при этом деформируется и образец. В частности, возникает огромная деформация кручения [13]: сдвиг на поверхности превышает 10^-4 в поле 0.1-1 V/cm, что соответствует пьезомодулю ~10^-5 m/V – на 3-4 порядка выше рекордных значений для пьезоэлектриков. Такие образцы являются готовыми крутильными актюаторами, и для возбуждения крутильных колебаний нет необходимости использования внешних приводов. Подобные свойства проявляет ряд квазиодномерных соединений с ВЗП [6], но наиболее детальные исследования были проведены на TaS₃ ромбической модификации (в дальнейшем – просто TaS₃). Это соединение, вырастающее в виде вискеров, переходит в состояние ВЗП при 220 К [12], а наибольшие углы кручения, δj, наблюдаются в области азотной температуры [6],[13].

Актуальная задача для дальнейшего исследования кручения – научиться детектировать крутильные колебания без применения дополнительных устройств. Её решение позволит повысить частоты колебаний, уменьшить размеры образцов, а также упростить измерительную технику, в том числе, криогенную. Исследования проводимости TaS₃ в зависимости от δj показали, что при температуре близкой к азотной в полях E > E_t наблюдается заметное тензосопротивление («торсиосопротивление») [14][15][18]. Относительная модуляция напряжения, нормированная на поверхностный сдвиг G, достигает 1–10 [18]. Таким образом, модуляция проводимости при крутильных колебаниях может быть источником сигнала, позволяющего детектировать резонанс.

Подчеркнём, что даже если такой образец подвесить над затвором, при кручении заряд на образце не будет модулироваться, и в обычном виде методика ГЧМ не применима. По этой же причине, эту методику почти невозможно использовать для детектирования изгибных резонансных колебаний высших мод.

Крутильные резонансные колебания удавалось детектировать и ранее по модуляции сопротивления образцов TaS₃ [14]. Для этого к середине подвешенного образца прикреплялся дополнительный контакт – гибкая проволока. Через этот контакт по одной половине образца пропускался переменный ток, вызывающий кручение, а по другой – постоянный, для детектирования модуляции проводимости. Это было нужно, чтобы разделить каналы переменного напряжения актюатора и приёмника, поскольку их частоты совпадали.

В данной работе применён метод ГЧМ. В этом случае необходимость разделения каналов актюатора и приёмника отпадает: на выходе напрямую измеряется сигнал пропорциональный производной амплитуды модуляции сопротивления образца, R_s, по частоте. Для демонстрации методики выбраны относительно большие по размерам образцы (длиной ~1 мм, шириной – несколько mm), на которые были наклеены микрозеркала. Это позволило одновременно контролировать колебания с помощью оптической методики. Однако применение микрозеркал сильно понижает частоты колебаний, и, в перспективе, методику планируется использовать для исследования ВЧ колебаний образцов без зеркал, в том числе, наноразмерных.

 

 

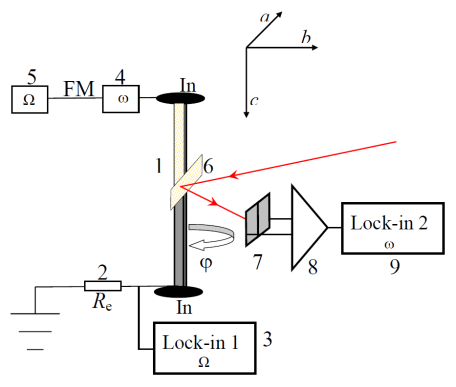
Рис. 1. Схема детектирования резонансных крутильных колебаний методом ЧМ с одновременным оптическим контролем колебаний.
1 – образец (вискер TaS₃), 2 – эталонное сопротивление, 3 – СД, 4 – генератор, задающий ток, 5 – модулирующий генератор.
Оптическая схема: 6 – зеркало, 7 – двухсекционный фотодиод, 8 – усилитель, 9 – СД.

На рис. 1 показана схема измерений. Образец 1 подвешен между индиевыми контактами. Половина образца покрыта золотом, шунтирующим образец. В этом случае ток протекает через объём образца только по другой его половине. В ней возникает закручивающее усилие, а первая половина играет роль пассивной растяжки [16]. Такая конфигурация образца [17][18][19] аналогична конфигурации со свободно подвешенным контактом [13], но проще в изготовлении. Переменное напряжение на частоте w, V=V₀cos(wt), подаётся на образец, заземлённый через малое эталонное сопротивление        R_e <<R_s – 2 на рис. 1: обеспечивается режим заданного напряжения. Напряжение V₁, пропорциональное току, подаётся с эталонного сопротивления на синхронный детектор СД1 (3): V₁=IR_e=VsR_e=V₀cos(wt)R_es₀(1+δj₀Πcos(wt+Φ)). В результате получаем:

 

V₁=V₀R_es₀(cos(wt)+δj₀Πcos(2wt+Φ)/2+δj₀Πcos(Φ)/2),           (1)

 

где s – проводимость образца, а – коэффициент относительного «торсиосопротивления». Вследствие крутильной деформации, δj=δj₀cos(wt), проводимость модулируется: s=s₀(1+δj₀Πcos(wt+Φ)), где Φ – сдвиг фазы колебаний относительно V₀. Последнее слагаемое в скобках – и есть постоянная составляющая в V₁, пропорциональная δj₀.

На вход «ЧМ» генератора 4, настроенного на частоту w, подаётся модулирующее напряжение с другого генератора 5 с частотой Ω, просуммированное с медленно меняющимся постоянным напряжением. Это позволяет медленно изменять величину w, одновременно модулируя её: w=w_ср(1+δwcos(Ωt)), где (Q–добротность резонанса). Величина δj₀ также модулируется с частотой Ω; амплитуда модуляции δj₀ оказывается пропорциональной производной δj₀ по w. Именно эту компоненту сигнала измеряет СД1 на опорной частотой Ω (третий член в (1)), отфильтровывая высокочастотные первый и второй члены (1). Поэтому, на зависимости сигнала на выходе СД1 от w в области резонанса следует ожидать зигзаг, – производную от максимума.

Аналогично измерения можно проводить в режиме заданного тока: на вход СД1 подаётся напряжение с образца, равное произведению его сопротивления и тока. Однако такая методика применима только при относительно низких w и R_s (в нашем случае, wR_s<~(1 nF)^-1).

Отметим, что Φ также зависит от w, что нужно учесть при дифференцировании δj₀cos(Φ) по w. В резонансе cos(Φ) обращается в 0, что должно усложнять вид сигнала [9]. В нашем случае некоторое запаздывание между V₁ и крутящим моментом [6] приводит к тому, что в резонансе Φ¹90°, и мы наблюдали зависимость V₁ от w типа производной от максимума. Различные виды особенностей в резонансе при различных Φ подробно рассмотрены в [9].

Для оптического контроля колебаний [13] на образец было наклеено микрозеркало 6 (рис. 1). Лазерный луч, отражаясь от зеркала, попадает на двухсекционный фотодиод 7, так что сигнал на выходе фотодиода оказывается пропорционален δj. Через усилитель 8 сигнал подаётся на другой детектор, СД2 (9), работающий на опорной частоте w. Сигнал на выходе СД2 пропорционален δj₀.

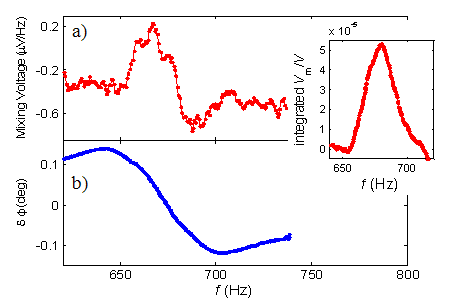
На рис.2,3 показаны зависимости одновременно измеренных сигналов СД1 (а) и СД2 (б) в зависимости от w для двух образцов TaS₃ – №1 и № 2, соответственно. Микрозеркало на образце №2 длиннее, чем на № 1, поэтому частота первого крутильного резонанса, 680 Hz, на образце №2 существенно ниже, чем на №1 – 20 kHz. Соответственно, измерения на образце № 1 проводились в режиме заданного напряжения, а на № 2 – заданного тока. Показания СД1 пересчитаны в ток (образец № 1) или напряжение (№ 2), разделены на амплитуду модуляции частоты, и в таком виде представлены на рис. 2a и 3a, соответственно. На обоих рисунках ясно виден зигзаг в области частоты резонанса. Аналогичная по форме зависимость получается на выходе СД2, настроенного приблизительно в фазе с поданным напряжением (Рис 2b и 3b). В квадратуре с напряжением наблюдается максимум отклика (зависимости не приведены). Отметим, что из-за больших отклонений зеркал, значения углов на рис 2b и, особенно, рис. 3b заметно искажены.

 

 

Рис. 2. Образец №1. Показания СД1, пересчитанные в ток на кГц (a) и СД2, пересчитанные в угол (b), в зависимости от частоты, снятые одновременно. Режим заданного напряжения (рис. 1), размах ±700 mV (пороговое напряжение – 80 mV). Фазы обоих СД близки к 0. На вставке: показания СД1, проинтегрированные по частоте и нормированные на ток. Длина незапылённой части L=1.1 mm, ширина w=6.4 mm. T=96 K

 

 

Рис. 3. Образец №2. Показания СД1, пересчитанные в напряжение на Гц (a), и СД2, пересчитанные в угол (b), в зависимости от частоты, снятые одновременно. Режим заданного тока, размах ±7.4mА (пороговый ток – 0.48 mА). Фазы обоих СД близки к 0. На вставке: показания СД1, проинтегрированные по частоте и нормированные на напряжение. Длина незапылённой части L=1.2 mm, ширина w=8 mm. T=90 K.

Наблюдение особенностей, представленных на рис. 2a и 3a, означает, что нам удалось детектировать крутильный резонанс без использования оптической схемы. Помимо упразднения оптической схемы, важнейшим преимуществом предложенной методики является её частотная характеристика. Частота напряжения, подаваемого на образец, ограничена лишь его внутренней ёмкостью и может составлять гигагерцы. Это значит, что предел детектирования колебаний определяется максимальной частотой резонансных колебаний (с амплитудой, достаточной для заметной модуляции сопротивления). Для наноразмерных образцов эти частоты могут приближаться к гигагерцам. Приведём оценку. Основная частота крутильных колебаний не зависит от его ширины w и равна

 

                                    (2)

 

где L – длина образца, m - модуль сдвига, r – плотность. Из (2) очевидна необходимость укорочения образцов для повышения w₀. Подставляя для TaS₃ m=5 GPa [11], r=6.4–10³ kg/m³ [12], L=1 mm, получаем .

Интегрируя кривые на Рис. 2а и 3а, получаем максимумы. Их физический смысл – изменение тока или напряжения на образце в результате модуляции проводимости. Нормируя сигнал в максимуме на ток (рис. 2) или напряжение (рис. 3), получаем относительную модуляцию проводимости и , соответственно. При этом δj₀~0.08° и ~0.25°, а сдвиг на краях образца, и , соответственно. Поделив δs/s на G, получаем 30 для образца №1 и 4 – для образца № 2. Эти безразмерные величины характеризуют тензорезистивный эффект, причём в данном случае он вызван сдвиговой деформацией. Учитывая, что в линейном приближении сдвиг не приводит к изменению объёма, следует отметить, что величина тензорезистивного эффекта весьма велика. Эти значения находятся в согласии с проведёнными ранее оценками [18]: (δs/s)/G = 1–10.

Приблизительность оценок связана с нелинейностью и пороговым видом зависимостей кручения и модуляции сопротивления от тока. Эта модуляция вызвана изменением условий зацепления ВЗП за примеси (пиннинга) при деформации [18] и определяется индивидуальными свойствами образца. Величина (δs/s)/G растёт с ростом напряжения примерно как E- E_t [15][18], поэтому для увеличение сигнала СД1 следует прикладывать напряжение значительно выше E_t. При этом, однако, резко возрастают внутренние механические потери [11] и падает добротность резонатора.

Итак, мы продемонстрировали, что образцы квазиодномерного соединения c ВЗП TaS₃, являясь уникальными актюаторами, могут быть и детекторами резонансных колебаний. Переменный ток, протекающий через образец, содержит в себе информацию об амплитуде этих колебаний. Эту информацию можно извлечь, используя технику ГЧМ. Предложенная методика представляется наиболее перспективной для исследования ВЧ колебаний, прежде всего, в образцах микронных и нанометровых размеров.

 

Авторы благодарны R.E. Thorne за предоставление образцов, M. Deshmukh, S. Sengupta и С.В. Зайцеву-Зотову за ценные замечания. Работа проводилась при поддержке РФФИ (грант 11-02-01282), Министерства образования и науки России (соглашение 8571), а также в рамках Программы Президиума РАН №27 «Основы фундаментальных исследований нанотехнологий и наноматериалов», Программы РАН «Новые материалы и структуры» и Международной Европейской лаборатории «Физические свойства когерентных электронных состояний в твёрдых телах» при поддержке НЦНИ (Франция), РАН и РФФИ.

Литература

[1]              K. Jensen, K. Kim, A. Zettl. „An atomic-resolution nanomechanical mass sensor“. // Nat. Nanotech. 2008. V. 3. P. 533 – 537.

[2]              A.D. O’Connell, M. Hofheinz, M. Ansmann et al. „Quantum ground state and single-phonon control of a mechanical resonator“. // Nature 2010. V. 464. P. 697–703.

[3]              Masmanidis S. C., Karabalin R. B., Vlaminck I. De et al. “Multifunctional Nanomechanical Systems via Tunably Coupled Piezoelectric Actuation” // Science 2007. V. 317. P. 780-783.

[4]              S.J. Papadakis, A.R. Hall, P.A. Williams et al. “Resonant Oscillators with Carbon-Nanotube Torsion Springs” // Phys. Rev. Lett. 2004. V. 93. P. 146101(1-4).

[5]              R. Gao, Z.L. Wang, Z. Bai et al. “Nanomechanics of Individual Carbon Nanotubes from Pyrolytically Grown Arrays” // Phys. Rev. Lett. 2000. V. 85. P. 622-625.

[6]              V.Ya. Pokrovskii , S.G. Zybtsev, V.B. Loginov. et al. “Deformations of charge-density wave crystals under electric field”. // Physica B 2009. V 404. P. 437–443.

[7]              V. Sazonova, Y. Yaish, Y. Ustunel et al. “A tunable carbon nanotube electromechanical oscillator”. // Nature 2004. V. 431. P. 284-287.

[8]              V. Gouttenoire, T. Barois, S. Perisanu et al. “Digital and FM Demodulation of a Doubly Clamped Single-Walled Carbon-Nanotube Oscillator: Towards a Nanotube Cell Phone”. // Small 2010. V. 6. P. 1060-1065.

[9]              V. Sazonova. “A Tunable Carbon Nanotube Resonator” // Ph.D. Thesis, Cornell University http://www.lassp.cornell.edu/lassp_data/mceuen/homepage/Publications/Thesis_Sazonova.pdf

[10]         S. Sengupta, N. Samudrala, V. Singh. et al. “Plasmon mode modis the elastic response of a nanoscale charge density wave system”. // Cond-mat/12084453 (2012)

[11]         J.W. Brill  in Handbook of Elastic Properties of Solids, Liquids, and Gases (Editors-in-ChiefMLevy,HE Bass,RRStern) Vol. II Elastic Properties of Solids: Theory, Elements and Compounds, Novel Materials, Alloys, and Building Materials (Ed. M Levy) (San Diego: Academic Press, 2001) Ch. 10, p. 143

[12]         P. Monceau. “Electronic crystals: an experimental overview”. // Advances in Physics 2012. V. 61. P. 325-581.

[13]         V.Ya. Pokrovskii, S.G. Zybtsev, I.G. Gorlova. “Torsional Strain of TaS₃ Whiskers on the Charge-Density Wave Depinning”. // Phys. Rev. Lett. 2007. V. 98. P. 206404.

[14]         V.Ya. Pokrovski, S.G. Zybtsev. “Self-sensitive torsional microresonators based on a charge-density wave system”. // Cond-mat/07082694 (2007)

[15]         J. Nichols, D. Dominko, L. Ladino, J. Zhou, J.W. Brill. “Characterization of the torsional piezoelectriclike response of tantalum trisulfide associated with charge-density-wave depinning” // Phys. Rev. B 2009. V. 79. P. 241110(R) V. 80. P. 039903(E).

[16]         Если ток пропускать через весь образец, то, в первом приближении, в нём возникает однородное закручивающее усилие [13]. Если оба его конца закреплены, деформации не возникнет.

[17]         С.Г. Зыбцев, М.В. Никитин, В.Я. Покровский. «Ступеньки Шапиро в кручении квазиодномерного проводника TaS₃». // Письма в ЖЭТФ 2010. Т. 92, С. 448-453.

[18]         В.Я. Покровский , С.Г. Зыбцев, М.В. Никитин и др. // УФН 2012. «Высокочастотные, «квантовые» и электромеханические эффекты в квазиодномерных кристаллах с волной зарядовой плотности», обзор, УФН 2013. Т. 183. С. 33

[19]         H. Zhang, J. Nichols, and J.W. Brill. “Torque and temperature dependence of the hysteretic voltage-induced torsional strain in tantalum trisulfide”. // Phys. Rev. B 2011. V. 84. P. 125134.