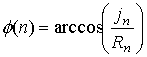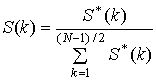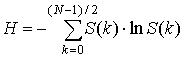Количественная оценка сложности контура медицинских изображенний

УДК 621.391

КОЛИЧЕСТВЕННАЯ ОЦЕНКА СЛОЖНОСТИ КОНТУРА МЕДИЦИНСКИХ ИЗОБРАЖЕНИЙ

С. А. Останин, А. М. Шайдук

Алтайский государственный университет, г. Барнаул

Получена 18 февраля 2013 г.

Аннотация. Предложены две количественные характеристики сложности контура изображения. Описан способ их получения и приведены результаты количественной оценки сложности контуров изображений.

Ключевые слова: медицинские изображения, сложность контура.

Abstract. Two quantitative characteristics of the contour image are proposed. The process for their preparation and the results of a quantitative evaluation of image edges is described.

Keywords: medical image, complexity of image edges.

При получении и последующем анализе томографических изображений регистрируются количественные параметры области интереса. К ним относится, например, размер области, плотность изображения, записанная в DICOM файле в единицах Хаунсфилда, среднеквадратичное отклонение плотности, фрактальная размерность [1-12]. Предполагается, что эти характеристические параметры, хотя бы в принципе, несут информацию о наличии патологии в области интересов, а, возможно, и позволяют дифференцировать вид заболевания [13-17].

Однако, часть параметров, на которые врачи – диагносты считают необходимым обращать внимание и указывать в заключении, носит качественный характер. Характерный пример – характеристики контура возможной патологии или органа в области интересов. Часто можно встретить такие характеристики контура, как «гладкий», «неровный», «бугристый», «фистончатый» и т.п.[18-22]. Подобные характеристики контура являются слишком необъективными, зависящими от эксперта и неудобными для построения информационной диагностической системы. В настоящей работе сделана попытка ввести количественные характеристики сложности контура медицинского изображения.

С формальной точки зрения изображение (для одного томографического среза) в DICOM формате можно представить в виде функции , где – хаунсфилдовская плотность ткани в точке плоского среза с координатами . На языке изображений – координаты пикселя изображения по строке и по столбцу, а величина пропорциональна яркости соответствующего пикселя.

Проблема выделения контура патологии может решаться различными способами [23-32] и не является основной задачей, рассматриваемой в данной работе. Для получения конкретных результатов в настоящей работе применялся наиболее простой метод – эксперт указывал пиксель , принадлежащий контуру. Далее исходное изображение превращалось в бинарное следующим алгоритмом: если , то , если , то .

После преобразования исходного изображения в бинарное был использован следующий алгоритм. Выделялась точка с координатами , заведомо принадлежащая границе изображения, и ей присваивался номер 1. Поскольку точка принадлежала границе, существует соседний пиксель с яркостью 0. Начиная с этого пикселя, просматривались соседние с пиксели по часовой стрелке. После определения координат пикселя с ненулевой яркостью ему присваивался номер 2, после чего процедура повторялась.

Итогом работы алгоритма было множество координат соседних пикселей, являющихся пронумерованными координатами контура, , , ... ... . Алгоритм завершен при одновременном выполнении условий , (таким образом, контур замыкался).

Для количественной характеристики полученного контура предварительно определялись его сигнатуры с помощью методики, аналогичной описанной в [13]. Определялся центр бинарного изображения :

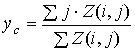, . (1)

(здесь суммирование выполняется по всем возможным ).

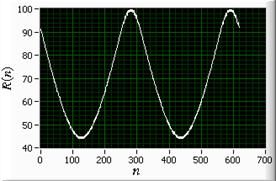
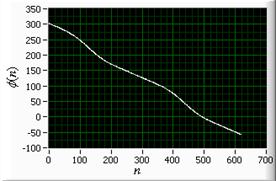
Далее в полярной системе координат с центром в точке определялся модуль радиус-вектора всех точек контура

, (2)

и полярный угол

, (3)

Множество модулей радиус-вектора и полярных углов и являются сигнатурами выделенного контура.

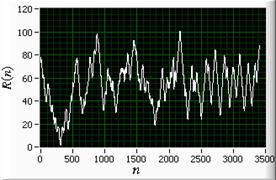
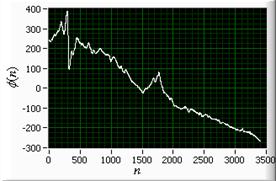
Сигнатуры будут использованы нами для получения количественных характеристик сложности контура. Выясним, чем отличаются сигнатуры простых контуров от сигнатур сложных контуров. Рассмотрим, в качестве примера, изображения разной сложности (рисунок 1 а, г, ж).

а б в

г д е

ж з и

Рис. 1. Изображения: а – «эллипс» , г – «ромашка», ж – «губка».

Сигнатуры модуля радиус-вектора: б – «эллипса» , д – «ромашки», з – «губки». Сигнатуры угла: в – «эллипса» , е – «ромашки», и – «губки».

Размер каждого квадрата 200х200 пикселей. Контуры первых двух фигур (рисунок 1 а, г) обладают симметрией, но отличаются формой. Контур третьего изображения ассиметричен (рисунок 1 ж) и существенно сложнее. Получим для этих контуров сигнатуры модуля радиус-вектора (рисунок 1 б, д, з) и сигнатуры угла (рисунок 1 в, е, и), используя выражения (2) и (3).

Рассмотрим сигнатуры радиуса контуров. Из рисунка 1 видно, что разные по сложности контуры имеют разные по сложности сигнатуры, следовательно, задачу оценки сложности контура, можно решить, например, с помощью количественных характеристик сложности сигнатур.

Известные характеристики оценки вариации значений одномерного ряда (среднеквадратичное отклонение, энтропия, характеристики шероховатости поверхности установленные ГОСТ 2789-73) не отражают особенностей его структуры (морфологии). Как следствие, эти характеристики не специфичны для различных по сложности сигнатур. В качестве иллюстрации укажем, что, например, среднеквадратичные отклонения сигнатур радиус-вектора контуров «эллипс», «ромашка», «губка» (рисунок 1) имеют значения 18.7, 16.7 и 18.3 соответственно, а величина энтропия Шеннона сигнатур – 2.2, 2.3, 2.0 соответственно. Из сравнения указанных значений видно, что эти количественные характеристики практически одинаковы для существенно разных по сложности контуров, то есть, не отражают сложность контуров. В некоторых случаях для оценки сложности контура медицинских изображений используют фрактальную размерность сигнатуры, величина которой определяется структурой контура. Ограничением применения этой характеристики является условие: сигнатура должна иметь фрактальную структуру.

Предлагаемые нами характеристики сложности контура свободны от указанных недостатков. Первая характеристика построена на основе сигнатуры радиус-вектора. Проанализируем структуру сигнатур (рисунок 1). Как видно из рисунков 1 б, д, простым, симметричным контурам соответствуют периодические сигнатуры. Сложный контур имеет апериодическую сигнатуру радиуса. Следовательно, по степени периодичности сигнатуры радиуса контура можно судить о его сложности.

Для оценки степени периодичности сигнатуры радиуса контура используем спектральный анализ. Будем считать, что чем меньше полоса спектра сигнатуры радиуса контура, тем более периодична сигнатура. Спектральную плотность мощности центрированной сигнатуры радиуса

(4)

вычислим как

(5)

где символом обозначено математическое ожидание, символом – преобразование Фурье, – номер гармоники спектра (). Процедуру центрирования (4) выполняем с тем, чтобы уменьшить относительную погрешность оценки мощности гармоник спектра с . Кроме того, полагаем, что сложность определяется мощностью гармоник с , а величина характеризует средний радиус контура (эффективный размер) и не влияет на сложность контура. Выполним нормировку спектральной плотности мощности на мощность всех гармоник :

. (6)

Нормированная спектральная плотность мощности представляет собой долю мощности сигнатуры, приходящуюся на гармонику номер k.

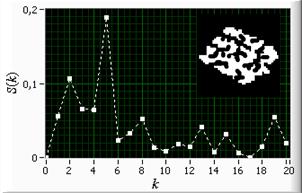
Нормированные спектральные плотности мощности сигнатур радиуса контуров «эллипс», «ромашка», «губка» показаны на рисунке 2 (для удобства сравнения показана только часть спектра). Из сравнения рисунков 2 а и 2 б видно, что спектры контуров, обладающих симметрией, имеет схожую структуру в виде узких спектральных линий, в которых сосредоточена почти вся мощность. Относительная мощность гармоники контура «ромашка» (рисунок 2 б) несколько меньше единицы, так как сигнатура контура (рисунок 1 д) не синусоидальна. Существенное количественное различие состоит в численном значении гармоники k. Величина k соответствует количеству «лепестков» контура. Спектр контура «губка» (рисунок 2 в) отличается от спектров симметричных контуров (рисунки 2 а, б) шириной полосы и структурой: спектр образует большое количество гармоник сравнимых по порядку величины.


			б
	а

Рис. 2. Нормированные спектральные плотности мощности сигнатур контуров: а – «эллипс», б – «ромашка», в – «губка».

Сравнительный анализ спектров (рисунок 2 а, б, в) показывает, что сложность контура отражается в структуре спектра сигнатуры радиуса . Заметим, что нормированная спектральная плотность мощности (6) представляет собой вероятность того, что сигнатура радиуса имеет гармонику с номером k. Таким образом, спектральную плотность мощности можно интерпретировать как плотность распределения вероятности по гармоникам k. Следовательно, для характеристики распределения мощности сигнатуры радиуса по гармоникам k можно использовать модифицированную информационную энтропию Шеннона в виде

. (7)

Из свойств энтропии (7) следует, что сигнатурам, имеющим спектр в виде единственной спектральной линии, будет соответствовать нулевая энтропия. С ростом ширины полосы спектра сигнатуры значение энтропии увеличивается.

Предложенный метод оценки сложности контура реализован с использованием системы визуального программирования LabVIEW. Тестирование программы автоматической оценки сложности контура выполнено на 26 изображениях контуров различной сложности. В таблице 1 приведена часть результатов вычисления значения энтропии для гармоник сигнатур радиуса некоторых искусственно созданных контуров. Видно, что величина энтропии Н растет со сложностью изображения контура. Это дает основания для использования энтропии в качестве меры сложности контура.

Таблица 1. Энтропии гармоник сигнатур искусственных контуров

Контур	H	Контур	H
	0,09		2,11
	0,36		2,24
	0,73		3,17
	1,62		3,35

Дополнительным достоинством предлагаемого метода оценки сложности формы контура изображения является слабая зависимость энтропии от размера контура. Это особенно актуально при анализе медицинских изображений полученных аппаратами с разной разрешающей способностью. Изменение масштаба изображения не приводит к существенному изменению энтропии. Можно показать, что это следует из инвариантности нормированного спектра (6) относительно масштаба сигнатуры. Масштабирование изображения контура изменяет мощность гармоники с , но предварительное центрирование (4) сигнатуры минимизирует вклад этой гармоники в спектр и, в соответствии с (7), не влияет на величину характеристику сложности H.

Для экспериментальной проверки справедливости этого утверждения в отношении изображений малого размера значение энтропии было вычислено для пяти квадратов (расположенных под углом к ортам) с длиной стороны от 200 до 1000 пикселей.

Относительное уменьшение энтропии при увеличении размера стороны квадрата в 5 раз составило величину около 0,017. С увеличением размера стороны квадрата энтропия монотонно убывает (рисунок 3) и экспоненциально стремится к значению 0,2575:

. (8)

Малая величина относительного изменения и экспоненциальная сходимость энтропии при масштабировании границы позволяет использовать характеристику H для сравнения сложности изображений полученных аппаратами с разной разрешающей способностью.

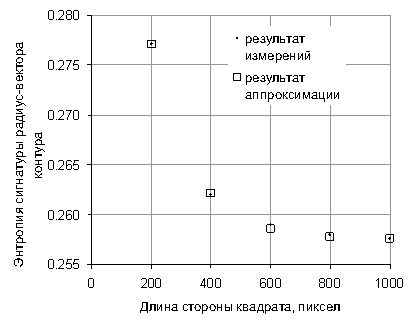
Рис. 3. Зависимость энтропии от размера контура квадратной формы.

В таблице 2 приведены изображения контуров медицинских изображений и соответствующие им значения энтропии для гармоник сигнатур радиуса контуров. Из таблицы видно, что разным контурам соответствуют разные значения энтропии. Таким образом показано, что предложенную характеристику можно использовать для оценки сложности, в том числе, контуров медицинских изображений.

Таблица 2. Энтропии гармоник сигнатур контуров медицинских изображений

Контур	H
	0,28
	0,93
	1,32

Теперь рассмотрим сигнатуру угла (примеры сигнатур угла показаны на рисунках 1 в, е, и) получаемую с помощью (3) и сформулируем еще одну независимую характеристику сложности контура.

Обратим внимание на тот факт, что сигнатура угла сложного контура (рисунок 1 и) уменьшается немонотонно. Каждый локальный максимум сигнатуры угла соответствует изменению направления вращения радиус-вектора . В форме контура это проявляется в виде незамкнутой петли, вытянутой под некоторым углом по отношению к радиус-вектору. Контуры с большим количеством петель воспринимаются как сложные. Таким образом, количеством локальных максимумов М сигнатуры можно оценить сложность контура изображения.

В качестве примера вычислим количество локальных максимумов М сигнатур угла контуров, представленных на рисунке 1. Сигнатуры угла (рисунки 1 в, е, и) контуров отличаются количеством локальных максимумов М: , , . Из сравнения полученных значений с изображением контуров следует: чем сложнее форма контура, тем выше значение М. Следовательно, параметр сигнатуры угла М можно использовать как независимую дополнительную характеристику сложности контура.

Таким образом, показано, что предложенные независимые характеристики H, М могут характеризовать сложность контуров изображений.

Литература

1. Rangayyan, RM. Fractal analysis of contours of breast masses in mammograms. / Rangayyan, RM, Nguyen, TM // Journal of Digital Imaging. – 2007. – Vol. 20(3). – Pp. 223–237. http://www.nonlinearbiomedphys.com/content/4/1/7.

2. Fractal analysis of medical images in the irregular region of interest / Oczeretko, Edvard, Borowska, Marta, Kitlas, Agnieszka et al. // BioInformatics and BioEngineering, BIBE 2008. 8th IEEE International Conference on / Dept. of Med. Inf., Univ. of Bialystok, Bialystok. – Vol. 1. – 2008. –October. – P. 6.

3. Reljin, Irini S. Fractal geometry and multifractals in analyzing and processing medical data and images / Reljin, Irini S, Reljin, Branimir D. // Archive of Oncology. – 2002. – Vol. 10(4). – Pp. 283–293.

4. Po-Whei Huang. Automatic classification for pathological prostate images based on fractal analysis / Po-Whei Huang, Cheng-Hsiung Lee // IEEE TRANSACTIONS ON MEDICAL IMAGING. – 2009. –July. – Vol. 28, no. 7. – Pp. 1037–1050.

5. Bhagwati,Charan. Early detection of breast cancer using self similar fractal method / Bhagwati, Charan, Sinha,G.R. // International Journal of Computer Applications. – 2010. –November. – Vol. 10, no. 4. – Pp. 39–43.

6. Medical images classification for skin cancer diagnosis based on combined texture and fractal analysis / Dobrescu, R, Dobrescu, M, Mocanu, M., Popescu, D. // WSEAS TRANSACTIONS on BIOLOGY and BIOMEDICINE. – 2010. –July. – Vol. 7, no. 3. – Pp. 223–232.

7. Papaioannou, V. Fractals and power law in pulmonary medicine. implications for the clinician / Papaioannou, V., Pneumatikos, I, // PNEUMON. – 2010. – July - September. – Vol. 23, no. 3. – Pp. 250–259.

8. Коновалов В.К. Прицельная 3d-реконструкция при изучении качественных характеристик поверхности шаровидных образований легких/ Коновалов В.К., Шойхет Я.Н., Федоров В.В. // Проблемы клинической медицины. – 2011. – № 3-4. – С. 20–25.

9. Леонов С.Л. Анализ погрешностей данных при мультиспиральной компьютерной томографии шаровидных образований легких / Леонов С.Л. Козлов Д.Ю., Колмогоров В.Г. и др.// Проблемы клинической медицины.

– 2011. № 3-4. – С. 16–19.

10. Ставицкий Р.В. Применение рентгеновской сканирующей денситометрии и компьютерной томографии для оценки эффекта лечения опухоли / Ставицкий Р.В., Лебеденко И.М., Бурдина И.И.// Медицинская техника. – 1995. – №3. – С. 20–28.

11. Останин С.А. Уточнение отношения между фрактальной размерностью и степенью спектра мощности сигнала / Останин С.А., Шайдук А.М.// Журнал радиоэлектроники. – 2012. – №8. http://jre.cplire.ru/jre/aug12/5/text.html

12. Шайдук А. М. Проблема стандартизации масштаба при вычислении фрактальной размерности медицинских изображений / Шайдук А. М., Останин С.А., Коновалов В.К.// Известия Алтайского государственного университета. – 2012. –T.№73. –С. 233–235.

13. Klonowski, W. Simple fractal method of assessment of histological images for application in medical diagnostics / Klonowski, W., Stepien, R., Stepien, P. // Nonlinear biomedical physics. – 2010. – Vol. 4. – Pp. 1–8. www.nonlinearbiomedphys.com/content/4/1/7.

14. Al-Kadi, O.S. Texture analysis of aggressive and nonaggressive lung tumor ce ct images / Al-Kadi, O.S., Watson, D. // IEEE TRANSACTIONS ON BIOMEDICAL ENGINEERING. – 2008. – Vol. 55, no. 7. – Pp. 1822–1830.

15. Taleb-Ahmed, A. Analysis methods of ct-scan images for the characterization of the bone texture: First results / Taleb-Ahmed, A., Dubois, P., Duquenoy, E. // Pattern Recognition Letters. – 2003. – Vol. 24. – Pp. 1971–1982.

16. Dar-Ren Chen, Ruey-Feng Chang, Chii-Jen Chen, Ming-Feng Ho, et al. Classification of breast ultrasound images using fractal feature // Clinical Imaging - 2005 - Vol. 29, Issue 4, Pp.235-245

17. Потапов А.А., Гуляев Ю.В., Никитов С.А., Пахомов А.А., Герман В.А. Новейшие методы обработки изображений / Под ред. А.А. Потапова.– М.: ФИЗМАТЛИТ, 2008.- 496 с. (монография - по гранту РФФИ № 07 - 07 - 07005).

18. Хофер М. Компьютерная томография. Базовое руководство. 2-е издание, переработанное и дополненное: — М.: Мед.лит., 2008. — 224 с.

19. Линденбратен Л.Д., Королюк И.П. Медицинская радиология и рентгенология (основы лучевой диагностики и лучевой терапии): Учебник.- М: Медицина, 2003.

20. Осадчий А.С., Вачев А.Н., Дмитриев О.В., Степанов М.Ю., Кириченко Н.Д. Опухоль каротидная (хемодектома) // Russian electronic journal of radiology - Том 2, №2, 2012, с.56-59.

21. Материалы Всероссийского конгресса лучевых диагностов/ М., МЕДИ Экспо, 2007 - 482с.

22. Савельева Г.М., Бреусенко В. Г. Соломатина А. А. и др. Диагностика опухолей и опухолевидных образований яичников // Росс. вест, акуш.-гинек. 2005. - №6. -С. 53-61.

23. Розенфельд А. Распознавание и обработка изображений с помощью вычислительных машин: Пер. с анг. - М.: Мир, 1972.

24. У.Прэтт. Цифровая обработка изображений. М.: Мир, 1982

25. T.Y.Kong, A.Rosenfeld. (Editors) Topological algoritms for digital image processing. Machine intelligence and pattern recognition. Volume 19. Elsevier. Amsterdam-Lausanne-New York-Oxford-Shanon-Tokyo. 1996.

26. Пытьев Ю.П. Морфологический анализ изображений// Доклад АН СССР. 1983. Т.269. № 5. С.1061 - 1064.

27. Marr D., Hildreth E. Theory of edge detection// Proc. R. Soc. (London). 1980. B207. Pp.187 - 217.

28. Canny. J. A computational approach to edge detection// IEEE Trans. Pattern Anal. Mach. Intell. 1986. №8. Pp.679 - 698.

29. Seeger U. and Seeger R. Fast corner detection in grey-level images// Pattern Recogn. Lett. 1994. №15(7). Pp.669 - 675.

30. Hua Lia, Anthony Yezzia, A hybrid medical image segmentation approach based on dual-front evolution model”, IEEE, 2005.

31. A. Tsai, A. Yezzi, and A.S. Willsky, “Curve evolution implementation of the mumford-shah functional for image segmentation, denoising, interpolation, and magniﬁcation,” IEEE Trans. on Image Processing, - 2001. - vol. 10, no. 8, Pp. 1169-1186

32. Мирошниченко С.Ю., Труфанов М.И., Анциферов А.В. Cпособ выделения контуров объектов изображения и устройство для его реализации / Патент RU 2383925 C2, 2007.