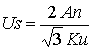Влияние шума и ошибок в определении аппаратной функции на восстановление изображения с помощью метода опорного изображения и фильтрации по методу Винера
А.
Ю. Зражевский, В. А. Коротков
ИРЭ им. В.А.Котельникова РАН,
Фрязинский филиал
Статья получена 24 февраля 2014 г.
Аннотация. В работе рассмотрено влияние шума и ошибок в определении аппаратной функции на результаты восстановления изображения с помощью метода опорного изображения и фильтрации по методу Винера.
Ключевые слова: радиовидение, миллиметровый диапазон волн, аппаратная функция, радиотепловое изображение, восстановление изображения, опорное изображение, метод Винера.
Abstract. The influence of noise and mistakes in definition of hardware function on results of recovery of the image by means of a method of the basic image and a filtration on Winer's method is considered in the work.
Key words: radio vision, millimetric wave band, hardware function, radio thermal image, recovery of the image, basic image, Winer's method.
Формирование изображений в любом диапазоне электромагнитных волн можно описать с помощью аппаратной функции (АФ) оптической системы, которая вносит искажения в конечный результат [1]. Кроме того, воздействие шумов и помех различного происхождения оказывает негативное влияние на процесс формирования изображений. Происходит это вследствие изменений в пространственном спектре. Для компенсации этих изменений применяются различные способы [1,3]. Эти методы нуждаются в определении параметров АФ и шумов (помех), влияющих на регистрируемый сигнал. Следует отметить, что рассматриваются только те шумы, которые добавляются к изображению, уже сформированному АФ.
Большую часть процессов, влияющих на формирование радиоизображения, можно описать в рамках уравнения свертки [1] :
![]() , (1)
, (1)
где D – область наблюдения, ![]() -
элементарная площадка в точке (x,y),
-
элементарная площадка в точке (x,y), ![]() -
аппаратная функция (АФ) системы,
-
аппаратная функция (АФ) системы, ![]() - исходное изображение,
- исходное изображение,![]() - изображение на выходе этой системы,
- изображение на выходе этой системы, ![]() -
аддитивный шум.
-
аддитивный шум.
Если перейти к спектральным ![]() представлениям
представлениям ![]() ,
, ![]() ,
, ![]() и
и ![]() , то в
частотной области пространственный спектр
, то в
частотной области пространственный спектр ![]() изображения на выходе системы
выражается через спектры исходного изображения -
изображения на выходе системы
выражается через спектры исходного изображения - ![]() , шума
-
, шума
- ![]() и АФ -
и АФ - ![]() :
:
![]() . (2)
. (2)
Откуда следует, что если
известен спектр АФ ![]() , то восстановленный спектр
исходного
, то восстановленный спектр
исходного![]() изображения
изображения ![]() можно
получить по формуле инверсной фильтрации:
можно
получить по формуле инверсной фильтрации:
![]() , (3)
, (3)
после чего «восстановленное»
изображение ![]() рассчитывается по формуле обратного
Фурье-преобразования:
рассчитывается по формуле обратного
Фурье-преобразования:
![]() .
(4)
.
(4)
При отсутствии шума ![]() и известной АФ системы достигается
идеальная реставрация изображения. Наличие шума в области малых значений
и известной АФ системы достигается
идеальная реставрация изображения. Наличие шума в области малых значений ![]() вызовет большие аддитивные ошибки и может
сделать восстановление изображения по формуле (3) невозможным.
вызовет большие аддитивные ошибки и может
сделать восстановление изображения по формуле (3) невозможным.
Проблемы при вычислении
спектра исходного изображения ![]() по формуле инверсной
фильтрации (3) вызываются наличием шума
по формуле инверсной
фильтрации (3) вызываются наличием шума ![]() и
ошибками в определении спектра аппаратной функции
и
ошибками в определении спектра аппаратной функции ![]() . Одним
из распространенных способов нахождения спектра
. Одним
из распространенных способов нахождения спектра ![]() из (2)
с учетом шума является Винеровская фильтрация [1].
из (2)
с учетом шума является Винеровская фильтрация [1].
Этот метод основан на рассмотрении изображения и шума как случайных процессов, и задача ставится следующим образом [1]:
Найти такую оценку ![]() для неискаженного изображения
для неискаженного изображения ![]() , чтобы среднеквадратичное отклонение этих
величин друг от друга было минимальным. Предполагается, что выполнены следующие
условия:
, чтобы среднеквадратичное отклонение этих
величин друг от друга было минимальным. Предполагается, что выполнены следующие
условия:
1. шум и неискаженное изображение не коррелированы между собой;
2. либо шум, либо неискаженное изображение имеют нулевое среднее значение;
3. оценка линейно зависит от искаженного изображения.
При выполнении этих условий минимум среднеквадратичного отклонения достигается на функции, которая задается в частотной области выражением
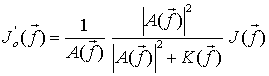 , (5)
, (5)
где
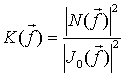 -
-
отношение энергетических спектров шума и неискаженного изображения. Отметим, что если шум равен нулю, то Винеровская фильтрация сводится к инверсной фильтрации.
Предложенный в [2] метод опорного изображения (МОИ) основан на фильтрации спектра изображения с применением для сравнения опорного изображения. Поэтому такой подход позволяет отфильтровывать помехи вне зависимости от их параметров и источника. Следует отметить, что в этом случае помехой (шумом) считается та часть спектра, которая энергетически превосходит некий порог, заданный усредненным спектром опорного изображения.
Анализ результатов применения МОИ [13] и фильтрации по Винеру [1] позволяет сделать вывод о том, что основными проблемами при восстановлении изображений являются ошибки в определении аппаратной функции и потери спектральной информации об изображении в результате формирования изображения оптической системой. Потери спектральной информации могут быть вызваны как оптической системой, так и шумами при измерении или записи изображения (ошибки квантования).
Сравним влияние уровня белого шума на восстановление изображения с помощью МОИ и метода Винера. В качестве аппаратной функции – АФ используем функцию Гаусса [7]:
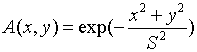 , (6)
, (6)
где ![]() предполагается
в дальнейшем равной 6. Уровень белого шума, действующего на сформированное АФ
изображение, задается его амплитудой -
предполагается
в дальнейшем равной 6. Уровень белого шума, действующего на сформированное АФ
изображение, задается его амплитудой - ![]() . В
качестве исходного изображения используем Рис.1.
. В
качестве исходного изображения используем Рис.1.

Рис.1. Исходное изображение. Размер: 200х300 пикселов.
После воздействия АФ с ![]() и белого шума с амплитудой
и белого шума с амплитудой ![]() изображение на Рис.1 примет вид,
представленный на Рис.2.
изображение на Рис.1 примет вид,
представленный на Рис.2.

Рис.2. Изображение после воздействия
АФ с ![]() и белого шума с
и белого шума с ![]() .
.
При вычислениях по методу
Винера [1,3] коэффициент ![]() - квадрат модуля
отношения шум/сигнал для данной пространственной частоты будем считать
константой и подбирать, исходя из визуальной оценки полученного результата.
Результаты расчетов при
- квадрат модуля
отношения шум/сигнал для данной пространственной частоты будем считать
константой и подбирать, исходя из визуальной оценки полученного результата.
Результаты расчетов при ![]() ,
, ![]() ,
, ![]() по
методу Винера и МОИ представлены на Рис.3-4.
по
методу Винера и МОИ представлены на Рис.3-4.
Сравнение Рис.3 и 4 показывает, что шумы в случае фильтрации Винера приводят к большей потере высоких пространственных частот. Восстановление изображения с помощью МОИ проявляет шумы в виде многочисленных артефактов, значительно снижающих качество восстановления. Для уменьшения влияния шумов на восстановление изображения с помощью МОИ можно использовать способ, описанный в [9].

Рис.3. Результат восстановления изображения
Рис.2 с помощью фильтрации Винера при ![]() .
.

Рис.4. Результат восстановления изображения Рис.2 с помощью МОИ [13].
Дополним алгоритм, описанный в [13] еще одним пунктом: если модуль спектра сформированного оптической системой изображения меньше предполагаемого уровня шумов на данной пространственной частоте, то устанавливаем амплитуду спектра восстановленного изображения на этой частоте равную нулю.
В рассматриваемом случае белого шума уровень шума считаем независящим от частоты и равным (4 дисперсии)
где ![]() - максимальная яркость.
- максимальная яркость.
При этих условиях результаты расчетов с помощью МОИ [13] представлены на Рис.5.

Рис.5 Результат восстановления изображения Рис.2 с помощью МОИ [13] с учетом (8).
Посмотрим, что произойдет,
если уровень шума увеличится в 20 раз (![]() ). В
этом случае изображение, сформированное АФ с
). В
этом случае изображение, сформированное АФ с ![]() будет
выглядеть как на Рис.6.
будет
выглядеть как на Рис.6.

Рис.6. Сформированное АФ с ![]() изображение с белым шумом амплитудой
изображение с белым шумом амплитудой ![]() .
.

Рис.7. Результат восстановления Рис.6
с помощью фильтрации Винера при ![]() .
.

Рис.8. Результат восстановления Рис.6 с помощью МОИ [13] с учетом (7).
Результаты восстановления по методу Винера и МОИ представлены на Рис.7 и 8 соответственно. Сравнение Рис.7 и 8 показывает, что эти методы дают близкие результаты.

Рис.9. Изображение после воздействия
АФ с ![]() и белого шума с
и белого шума с ![]() .
.
Пусть параметр АФ ![]() . Ошибка в его определении равна
. Ошибка в его определении равна ![]() . Обозначим ошибочно определенный параметр
аппаратной функции как
. Обозначим ошибочно определенный параметр
аппаратной функции как ![]() . Результаты восстановления
обоими методами при
. Результаты восстановления
обоими методами при ![]() и
и ![]() представлены
на Рис.10 и 11. Сравнение Рис.10 и 11 позволяет сделать вывод о том, что при
ошибке в определении
представлены
на Рис.10 и 11. Сравнение Рис.10 и 11 позволяет сделать вывод о том, что при
ошибке в определении ![]() в сторону уменьшения правильный
подбор
в сторону уменьшения правильный
подбор ![]() позволяет получить обоими методами
сравнимые результаты. Результаты восстановления обоими методами при
позволяет получить обоими методами
сравнимые результаты. Результаты восстановления обоими методами при ![]() и
и ![]() представлены
на Рис.12 и 13. Сравнение с Рис.12 и 13 позволяет сделать вывод о том, что при
ошибке в определении
представлены
на Рис.12 и 13. Сравнение с Рис.12 и 13 позволяет сделать вывод о том, что при
ошибке в определении ![]() в сторону увеличения метод
Винера очевидно проигрывает МОИ.
в сторону увеличения метод
Винера очевидно проигрывает МОИ.

Рис.10.
Результат восстановления Рис.9 с помощью фильтрации Винера при ![]() и
и ![]() ,
, ![]() ,
,![]() .
.

Рис.11. Результат восстановления Рис.9
с помощью МОИ с учетом (7) при ![]() и
и ![]() ,
, ![]() .
.

Рис.12. Результат восстановления Рис.9
с помощью фильтрации Винера при ![]() и
и ![]() ,
, ![]() ,
,![]() .
.

Рис.13. Результат восстановления Рис.9
с помощью МОИ с учетом (7) при ![]() и
и ![]() ,
, ![]() .
.
Рассмотрим теперь спектрально-локальные помехи. Будем считать, что в отличие от рассмотренных случаев, источник помех находится между объектом и оптической системой. Это могут быть как атмосферные явления (дождь, снег, неоднородность атмосферы), так и особенности самого объекта наблюдения (преимущественно ориентированные или периодически повторяемые элементы изображения).
Введем теперь спектрально локальную помеху на спектр изображения Рис.1. Пусть эта помеха занимает прямоугольные области симметричные относительно нуля и с координатами одной из них, заданной диагональю прямоугольника – (-5, 10; 5, 60). Полученное изображение и его спектр представлены на Рис.14-15. Введенные помехи представляют собой случайные комплексные числа . Они хорошо видны на спектре рис.15Б и проявляются на изображении в виде в среднем вертикально ориентированными случайными полосами. На рис.16 представлено изображение рис.14 после воздействия АФ с S=6. Видно, что полосы помех стали значительно шире за счет подавления высоких частот аппаратной функцией.

Рис.14. Изображение со спектрально локальной помехой.
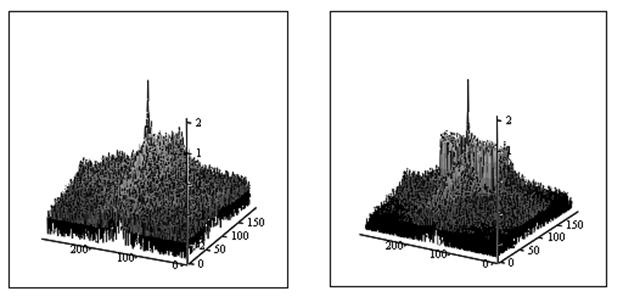
А Б
Рис.15. Амплитудные пространственные спектры, А – исходного изображение (Рис.1), Б - изображения со спектрально локальной помехой (Рис.14.).

Рис.16. Изображение со спектрально локальной помехой после воздействия АФ с S=6.
Видно, что полосы помех стали значительно шире за счет подавления высоких частот аппаратной функцией. С помощью МОИ изображение Рис.16 было восстановлено и результат представлен на Рис.17.

Рис.17. Результат восстановления Рис.16
с помощью МОИ с учетом (7) при ![]() .
.
В результате восстановления на основе МОИ спектрально локальная помеха была в значительной мере ослаблена за счет сравнения восстановленного амплитудного спектра с опорным спектром. Отфильтровать спектрально локальную помеху с помощью фильтрации по Винеру не удалось, поскольку одновременно с помехой удаляется и соответствующая часть спектральной информации об изображении. Результат неудачной попытки фильтрации по Винеру представлен на Рис.18.

Рис.18. Результат восстановления Рис.16
с помощью фильтрации Винера при ![]() ,
,![]() .
.
Выводы.
Ошибки в определении параметров в аппаратной функции, воздействие шумов и помех приводит к потере спектральной информации об изображении и уменьшает возможности восстановления исходного изображения. Сравнение результатов восстановления искаженного АФ и зашумленного изображения с помощью МОИ и методом Винера показывает примерно одинаковую эффективность обоих методов в фильтрации шумов. Следует отметить, что метод Винера существенно чувствительнее к ошибкам в определении параметров АФ, чем МОИ. Случай спектрально локальной помехи, источник которой воздействует на изображение до фильтрации АФ лежит вне области применимости метода Винера. Поэтому отрицательный результат фильтрации спектрально локальной помехи методом Винера неудивителен. В тоже время МОИ способен значительно ослаблять действие таких видов помех на результаты восстановления изображения.
Литература
1. Р. Гонсалес, Р. Вудс. Цифровая обработка изображений. М. «Техносфера», 2005, 1071 стр.
2. Зражевский А.Ю., Кокошкин А.В., Новичихин Е.П., Титов С.В., «Повышение качества радиоизображений». «Нелинейный Мир», № 9. 2010. с. 582-590.
3. Тихонов А.Н., Арсенин В.Я. - Методы решения некорректных задач. М.Наука, 1979.
4. Зражевский А.Ю., Голунов В.А, Смирнов М.Т., Новичихин Е.П., Лоскутов В.С., Ермаков Д.М. Поляризационные радиотепловые портреты.
5. А.Ю. Зражевский, А.В. Кокошкин. Влияние уровня боковых лепестков аппаратной функции на качество восстановленного изображения. // Журнал Радиоэлектроники [электронный журнал]. 2013. №4. URL: http://jre.cplire.ru/jre/apr13/8/text.pdf
6. В.А. Голунов, Г.К.Загорин, А.Ю. Зражевский, Б.А. Розанов, А.В. Соколов, Л.Ф. Черная. Пассивная радиолокация на миллиметровых волнах. В кн. Вопросы перспективной радиолокации. М., Изд. «Радиотехника», 2003, с. 393-463.
7. Зражевский А. Ю., Коротков В.А. Особенности восстановления искаженного оптической системой радиоизображения с помощью метода опорного изображения. // Журнал Радиоэлектроники [электронный журнал]. 2013. №4. URL: http://jre.cplire.ru/jre/apr13/3/text.pdf
8. А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков. Особенности применения инверсной фильтрации для восстановления изображений с учетом квантования яркости при записи в BMP файл. // Журнал Радиоэлектроники [электронный журнал]. 2013. №6. URL: http://jre.cplire.ru/jre/jun13/14/text.pdf
9. А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков. Исследование влияния количества уровней дискретизации размытого изображения на качество восстановления. // Журнал Радиоэлектроники [электронный журнал] 2013. №9. URL: http://jre.cplire.ru/jre/sep13/7/text.pdf
10. А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков. Восстановление искаженного оптической системой с неизвестными параметрами радиоизображения с помощью метода опорного изображения. // Журнал Радиоэлектроники [электронный журнал]. 2013. №9. URL: http://jre.cplire.ru/jre/sep13/9/text.pdf
11. А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков Влияние уровня боковых лепестков аппаратной функции на качество восстановленного изображения. Часть 2. Спектральный подход. // Журнал Радиоэлектроники [электронный журнал]. 2013. №11. URL: http://jre.cplire.ru/jre/nov13/4/text.pdf
12. Ю. В. Гуляев, А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков, В. А. Черепенин Коррекция пространственного спектра, искаженного оптической системой, с помощью метода опорного изображения. Часть 1. Классический метод опорного изображения (МОИ). // Журнал радиоэлектроники [электронный журнал]. 2013. №12. URL: http://jre.cplire.ru/jre/dec13/1/text.pdf
13. Ю. В. Гуляев, А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков, В. А. Черепенин Коррекция пространственного спектра, искаженного оптической системой, с помощью метода опорного изображения. Часть 2. Адаптивный метод опорного изображения (АМОИ). // Журнал радиоэлектроники [электронный журнал]. 2013. №12. URL: http://jre.cplire.ru/jre/dec13/2/text.pdf
14. Ю. В. Гуляев, А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков, В. А. Черепенин Коррекция пространственного спектра, искаженного оптической системой, с помощью метода опорного изображения. Часть 3. Универсальный опорный спектр. // Журнал радиоэлектроники [электронный журнал]. 2013. №12. URL: http://jre.cplire.ru/jre/dec13/3/text.pdf