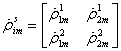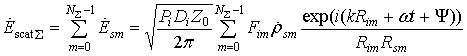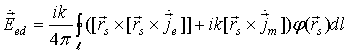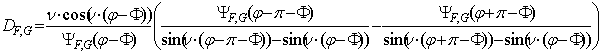УДК 621.396.961
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ХАРАКТЕРИСТИК РАССЕЯНИЯ ОБЪЕКТОВ ЛОКАЦИИ С ИМПЕДАНСНОЙ ПОВЕРХНОСТЬЮ
А. Б. Борзов, В. Б. Сучков, В. В. Ахияров, Ю. В. Каракулин
МГТУ им. Н.Э.Баумана
Статья получена 12 февраля 2014 г.
Аннотация. Приведена математическая модель характеристик рассеяния объектов локации сложной электрофизической структуры и формы, содержащих импедансные клиновидные структуры. Представлены выражения для определения эквивалентных токов на острой кромке, основанные на коэффициентах дифракции Уфимцева и теории Малюжинца. Приведены угловые диаграммы функций Уфимцева для поля от неравномерной части тока на импедансном клине и результаты расчетов эффективной площади рассеяния (ЭПР) импедансного цилиндра. Выполнено сравнение угловых диаграмм ЭПР импедансного цилиндра, полученных с использованием рассмотренной теории, и строгого решения методом интегральных уравнений.
Ключевые слова: физическая теория дифракции, клин с импедансными гранями, полигональная модель, рассеяние.
Abstract. The mathematical model of radar objects scattering characteristics with complex electrophysical structure and shape containing impedance wedge-shaped structures is presented. Formulas for equivalent edge currents definition, based on the modified Ufimtsev’ diffraction coefficients and Malyuzhinets theory are shown. Ufimtsev’ functions angular distribution for field from non-uniform currents and radar cross section (RCS) calculation for the impedance cylinder are shown. A comparison of RSC angular distributions with rigorous integral equation method is produced.
Keywords: physical theory of diffraction, impedance wedge, polygonal model, scattering.
В задачах расчета входных сигналов систем ближней радиолокации [1] возникает проблема анализа электромагнитных полей, отраженных от объектов сложной геометрической формы и электрофизической структуры. В последние годы в мире накоплен большой опыт по решению задач определения входных сигналов радиолокационных систем с использованием теории дифракции электромагнитных волн на объектах локации. Метод физической теории дифракции (ФТД) [2] позволяет учесть такие дифракционные явления, как рассеяние волн на острых кромках цели и двукратные переотражения волн между ее элементами.
Математическое моделирование характеристик рассеяния цели может быть основано на использовании ее полигональной модели, которая представляет поверхность объекта в виде совокупности простейших геометрических примитивов (плоский треугольный элемент и острая кромка). Наиболее передовым и мощным инструментом 3D моделирования сложных объектов на сегодняшний день является Creo 2.0 (Pro/Engineer), который позволяет синтезировать полигональную (фацетную) модель внешней поверхности объекта максимально точно и эффективно (рис. 1).
В работе [1] на основе метода ФТД обосновано использование выражения суммарного поля, рассеянного объектом локации, в виде когерентной суммы трех компонент [1]:
Первая компонента в соотношении (1) представляет собой величину результирующей напряженности электрического поля, рассеянного на всех плоских треугольных элементах, образующих полигональную модель объекта. Вторая составляющая является результирующей напряженностью поля, дифрагировавшего на острых кромках полигональной модели. Третья компонента поля определяется в результате суперпозиции полей рассеяния от треугольных элементов, для которых источники возбуждения вторичных волн наводятся за счет двукратных переотражений от других элементов полигональной модели.
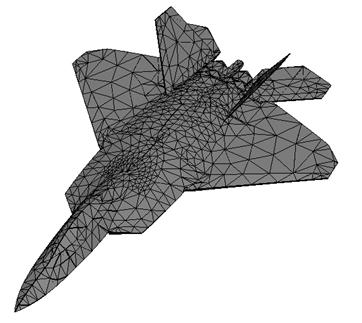
Рис. 1. Полигональная модель истребителя F-22
Компонента, обусловленная рассеянием волн на острых кромках цели, может вносить существенный вклад в результирующее рассеянное поле (1) на некоторых ракурсах наблюдения. Структура острых кромок и изломов на гладкой поверхности различных объектов приведена на рис. 2.
В соответствии с полигональным описанием геометрии цели и с использованием соотношений, полученных в [1], выражение для напряженности поля, рассеянного отдельным элементарным отражателем (треугольник или кромка), имеет вид:
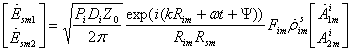 ,
(2)
,
(2)
 ,
(3)
,
(3)
 , (4)
, (4)
где ![]() - поляризационная матрица рассеяния
(ПМР) элемента, м;
- поляризационная матрица рассеяния
(ПМР) элемента, м;
![]() (
(![]() ) - компонента вектора напряженности
рассеянного поля в направлении векторов поляризации, В/м;
) - компонента вектора напряженности
рассеянного поля в направлении векторов поляризации, В/м;
![]() -
расстояние между элементарным отражателем (ЭО) и фазовым центром приемной
антенны, м;
-
расстояние между элементарным отражателем (ЭО) и фазовым центром приемной
антенны, м;
Pi – мощность сигнала, излучаемого передающей системой, Вт;
Di – КНД передающей антенны в направлении максимума излучения;
Z0=120p – волновое сопротивление воздуха, Ом;
![]() -
расстояние между фазовым центром антенны и началом системы координат ЭО, м;
-
расстояние между фазовым центром антенны и началом системы координат ЭО, м;
![]() -
круговая частота электромагнитных колебаний, рад/с;
-
круговая частота электромагнитных колебаний, рад/с;
Fim – значение функции направленности передающей антенны в направлении на m-й ЭО.
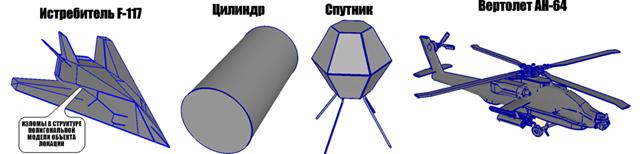
Рис. 2. Геометрия изломов гладкой поверхности объектов локации
ПМР описывает рассеивающие свойства элемента в зависимости от поляризационных характеристик передающей и приемной антенн. Каждый элемент ПМР (5) представляет собой комплексный коэффициент отражения [1,3], который определяется из следующего соотношения:
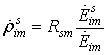 ,
(6)
,
(6)
где ![]() -
величина напряженности поля рассеяния, которая вычисляется для случая, когда
излучение и прием ведутся на линейной поляризации, В/м.
-
величина напряженности поля рассеяния, которая вычисляется для случая, когда
излучение и прием ведутся на линейной поляризации, В/м.
В соответствии с (6) комплексный коэффициент отражения ЭО выражается в [м] и не зависит от амплитуды электромагнитной волны, падающей на ЭО, а также от расстояния до фазового центра передающей антенны [3]. При этом комплексный коэффициент отражения находится в функциональной зависимости от геометрических размеров ЭО, его электродинамических параметров, а также от его ориентации в пространстве относительно передающей и приемной антенн.
Величина напряженности поля, рассеянного m-м элементом, принятая в апертуре приемной антенны, определяется в результате скалярного произведения вектора напряженности рассеянного поля вблизи приемной антенны на вектор поляризации приемной антенны в направлении на данный отражатель [1]:
![]() .
(7)
.
(7)
В результате имеем выражение для вычисления напряженности поля, рассеянного m-м отражателем, в апертуре приемной антенны:
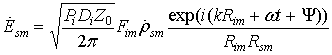 , (8)
, (8)
![]() . (9)
. (9)
С использованием соотношения (8), для каждого элемента вычисляется напряженность рассеянного поля в апертуре приемной антенны, а затем эти поля суммируются для получения напряженности результирующего дифракционного поля, рассеянного объектом:
Как было показано в [1] ЭПР цели представляется в виде суммы по всем комплексным коэффициентам отражения от элементов полигональной модели:
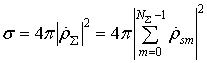 .
(11)
.
(11)
Для треугольника расчет ![]() осуществляется с учетом его
электродинамических параметров (диэлектрическая проницаемость, удельная
проводимость, радиопоглощающие покрытия), а соответствующая математическая
модель приведена в [1] и основана на методе физической оптики. При этом для
острых кромок (клиновидных структур) в [1] получены соотношения комплексного
коэффициента отражения только для случая идеальной проводимости кромки. Поэтому
представляет интерес определение комплексных коэффициентов отражения для
импедансных клиновидных структур (острых кромок). В основе электродинамической
модели взаимодействия плоской электромагнитной волны с острой кромкой лежит
физическая теория дифракции (ФТД), которая основана на уточнении поверхностного
тока, полученного методом физической оптики. Эта теория известна также под
названием метода краевых волн (МКВ). Согласно МКВ, полный ток, наведенный
падающим полем на поверхности треугольного элемента полигональной модели,
представляется в виде суммы тока
осуществляется с учетом его
электродинамических параметров (диэлектрическая проницаемость, удельная
проводимость, радиопоглощающие покрытия), а соответствующая математическая
модель приведена в [1] и основана на методе физической оптики. При этом для
острых кромок (клиновидных структур) в [1] получены соотношения комплексного
коэффициента отражения только для случая идеальной проводимости кромки. Поэтому
представляет интерес определение комплексных коэффициентов отражения для
импедансных клиновидных структур (острых кромок). В основе электродинамической
модели взаимодействия плоской электромагнитной волны с острой кромкой лежит
физическая теория дифракции (ФТД), которая основана на уточнении поверхностного
тока, полученного методом физической оптики. Эта теория известна также под
названием метода краевых волн (МКВ). Согласно МКВ, полный ток, наведенный
падающим полем на поверхности треугольного элемента полигональной модели,
представляется в виде суммы тока ![]() , полученного в
приближении физической оптики и тока
, полученного в
приближении физической оптики и тока ![]() , являющегося поправкой
к
, являющегося поправкой
к ![]() и обусловленного всеми эффектами, которые
не учитываются физической оптикой:
и обусловленного всеми эффектами, которые
не учитываются физической оптикой: ![]() . Токи
. Токи ![]() и
и ![]() считаются
соответственно равномерной и неравномерной частями полного тока. Поле, рассеянное
равномерной частью тока, является суммой геометрооптического и дифракционного
поля в приближении физической оптики. Неравномерная
часть тока обусловлена возмущениями, создаваемыми отклонениями поверхности от
бесконечной плоскости, например из-за ее изломов (ребер). Для вычисления
напряженности электрического поля, рассеянного острой кромкой, используется
схема радиолокации [3], представленная на рис. 3. Выражение для вектора
напряженности поля рассеяния острой кромки с произвольными электрическими
свойствами имеет вид [3]:
считаются
соответственно равномерной и неравномерной частями полного тока. Поле, рассеянное
равномерной частью тока, является суммой геометрооптического и дифракционного
поля в приближении физической оптики. Неравномерная
часть тока обусловлена возмущениями, создаваемыми отклонениями поверхности от
бесконечной плоскости, например из-за ее изломов (ребер). Для вычисления
напряженности электрического поля, рассеянного острой кромкой, используется
схема радиолокации [3], представленная на рис. 3. Выражение для вектора
напряженности поля рассеяния острой кромки с произвольными электрическими
свойствами имеет вид [3]:
где ![]() -
направляющий вектор отраженной волны из вершины кромки P1 в фазовый центр приемной антенны,
-
направляющий вектор отраженной волны из вершины кромки P1 в фазовый центр приемной антенны, ![]() -
функция Грина для данной задачи [1].
-
функция Грина для данной задачи [1].
Эквивалентные токи на
поверхности острой кромки ![]() определяются на основе
соотношений Нотта и Сеньора [3,4]:
определяются на основе
соотношений Нотта и Сеньора [3,4]:
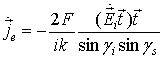 ,
,
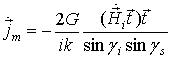 ,
(13)
,
(13)
где F, G – угловые
функции, которые определяют поле, рассеяное неравномерной частью тока (для
вертикальной и горизонтальной поляризации), ![]() -
пространственные углы между направляющими векторами
-
пространственные углы между направляющими векторами ![]() и
и ![]() и вектором
и вектором ![]() .
.
В соответствии с [1] комплексный коэффициент отражения острой кромки определяется следующим образом:
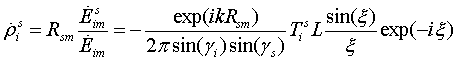 , (14)
, (14)
![]() , (15)
, (15)
где L – длина ребра, м; ![]() (
(![]() - проекция разностного вектора
- проекция разностного вектора ![]() на ось x).
на ось x).
Таким образом, задача
определения эквивалентных токов ![]() сводится к вычислению
функций F и G, которые определяют поле, рассеянное неравномерными токами вблизи
ребра клина. Для идеально проводящего клина данные функции хорошо известны [2]
и определяются в системе координат клина, как это показано на рис.3. Функции F
и G вычисляются с использованием следующих обозначений: a - внешний угол острой кромки P1P2 (рис. 4),
сводится к вычислению
функций F и G, которые определяют поле, рассеянное неравномерными токами вблизи
ребра клина. Для идеально проводящего клина данные функции хорошо известны [2]
и определяются в системе координат клина, как это показано на рис.3. Функции F
и G вычисляются с использованием следующих обозначений: a - внешний угол острой кромки P1P2 (рис. 4), ![]() - углы визирования
кромки для падающей и отраженной волн.
- углы визирования
кромки для падающей и отраженной волн.
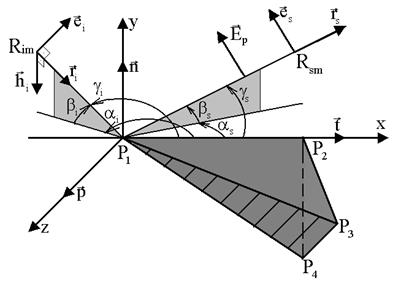
Рис. 3. Схема радиолокации острой кромки полигональной модели
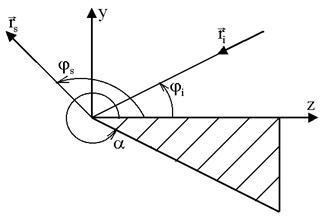
Рис. 4. Система координат для определения коэффициентов дифракции
Для идеально проводящего
клина в случае моностатической локации (![]() ) функции
F и G определяются соотношениями [2]:
) функции
F и G определяются соотношениями [2]:
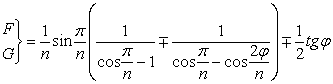 ,
, ![]() ,
(16)
,
(16)
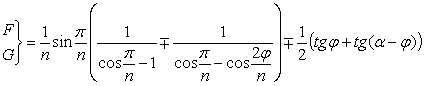 ,
, ![]() , (17)
, (17)
 ,
, ![]() ,
(18)
,
(18)
где ![]() , а
угол j отсчитывается от освещенной грани
клина.
, а
угол j отсчитывается от освещенной грани
клина.
Если обобщить выражения (16-18) на случай импедансного клина, рассмотренную теорию расчета поля можно использовать для локационных целей, поверхность которых обладает конечным импедансом. Для этого следует первые слагаемые в (16-18), которые имеют смысл коэффициентов дифракции, заменить коэффициентом дифракции Г.Д. Малюжинца [6-8]; вторые слагаемые, соответствующие дифракционному полю в приближении физической оптики, необходимо домножить на коэффициенты отражения от соответствующей грани клина для разных поляризаций:
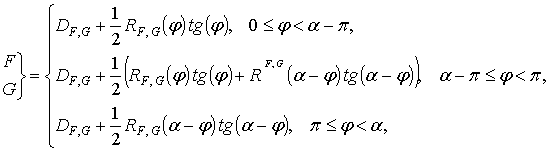 (19)
(19)
где D – коэффициент дифракции Г.Д.
Малюжинца, ![]() – коэффициенты отражения на
соответствующей поляризации:
– коэффициенты отражения на
соответствующей поляризации:
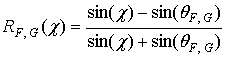 . (20)
. (20)
В формуле (20)
использованы следующие обозначения: ![]() ,
, ![]() , где
, где ![]() ,
, ![]() и
и ![]() -
относительные комплексные диэлектрическая и магнитная проницаемости (
-
относительные комплексные диэлектрическая и магнитная проницаемости (![]() и
и ![]() -
относительная диэлектрическая проницаемость и удельная проводимость граней
клина, которые полагаются идентичными).
-
относительная диэлектрическая проницаемость и удельная проводимость граней
клина, которые полагаются идентичными).
В соответствии с теорией Г.Д. Малюжинца, коэффициент дифракции определяется выражением [6-8]:
где
функция ![]() определена в работе [8]:
определена в работе [8]:
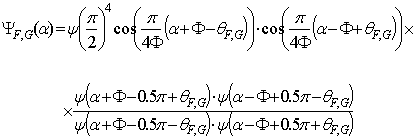 , (22)
, (22)
![]() -
функция Малюжинца [6]:
-
функция Малюжинца [6]:
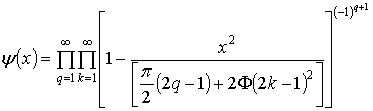 . (23)
. (23)
На основе соотношений (12-23)
получены зависимости модулей функций F и G от угла ![]() для идеально
проводящего (
для идеально
проводящего (![]() ) и импедансного клина с параметрами
) и импедансного клина с параметрами ![]() ,
, ![]() на
длине волны
на
длине волны ![]() см (рис. 5). Как видно из графиков,
зависимости для идеально проводящего клина полностью соответствуют аналогичным результатам,
которые были приведены в [2]. Далее с использованием соотношений (10-11) и (21-23)
на основе методики, приведенной в [1], определялась ЭПР цилиндра при обратном
рассеянии на двух различных поляризациях. Для верификации представленных
соотношений выполнялся сравнительный анализ результатов, которые были получены методом
ФТД на основе полигональной модели объекта и методом интегральных уравнений с
использованием программы САПР EMSS FEKO. В качестве
объекта для верификации использовался импедансный цилиндр с параметрами: радиус
см (рис. 5). Как видно из графиков,
зависимости для идеально проводящего клина полностью соответствуют аналогичным результатам,
которые были приведены в [2]. Далее с использованием соотношений (10-11) и (21-23)
на основе методики, приведенной в [1], определялась ЭПР цилиндра при обратном
рассеянии на двух различных поляризациях. Для верификации представленных
соотношений выполнялся сравнительный анализ результатов, которые были получены методом
ФТД на основе полигональной модели объекта и методом интегральных уравнений с
использованием программы САПР EMSS FEKO. В качестве
объекта для верификации использовался импедансный цилиндр с параметрами: радиус
![]() , длина образующей
, длина образующей ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Результаты расчетов ЭПР цилиндра и его полигональная модель с условиями локации
приведены на рис. 6. В соответствии с данным рисунком, погрешность при
вычислении ЭПР импедансного цилиндра методом ФТД с использованием коэффициента
дифракции Малюжинца по сравнению со строгим решением составляет в среднем 2-5
дБ во всем диапазоне углов, что говорит о достаточно хорошей точности
вычислений методом ФТД.
.
Результаты расчетов ЭПР цилиндра и его полигональная модель с условиями локации
приведены на рис. 6. В соответствии с данным рисунком, погрешность при
вычислении ЭПР импедансного цилиндра методом ФТД с использованием коэффициента
дифракции Малюжинца по сравнению со строгим решением составляет в среднем 2-5
дБ во всем диапазоне углов, что говорит о достаточно хорошей точности
вычислений методом ФТД.
|
а) |
б) |
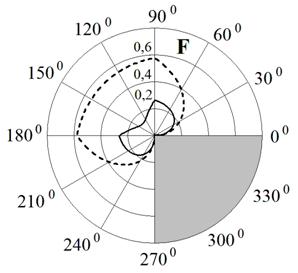
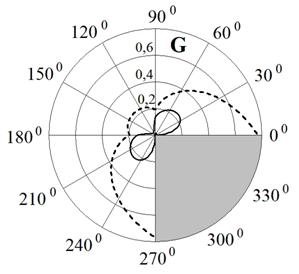
Рис. 5. Зависимости функций F и G от угла ![]() (сплошная кривая –
импедансный клин, штриховая кривая – идеально проводящий клин)
(сплошная кривая –
импедансный клин, штриховая кривая – идеально проводящий клин)
Таким образом, по результатам исследований можно сделать следующие выводы:
- представлено обобщение ФТД для задачи обратного рассеяния на импедансном клине;
- получены угловые функции F и G для импедансного клина, показана возможность использования данных функций для расчета характеристик обратного рассеяния от различных объектов;
- проведена верификация полученных соотношений для угловых функций F и G на основе численного моделирования ЭПР импедансного цилиндра, в результате которой показано, что погрешность расчетов ЭПР методом ФТД составляет в среднем 2-5 дБ по сравнению с методом интегральных уравнений.
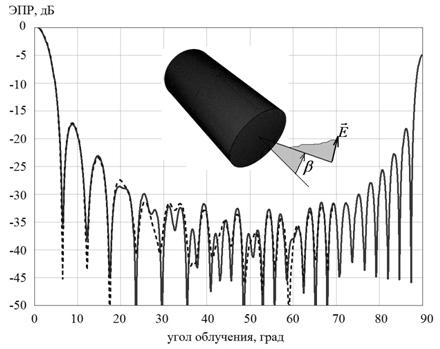
(а) – вертикальная поляризация
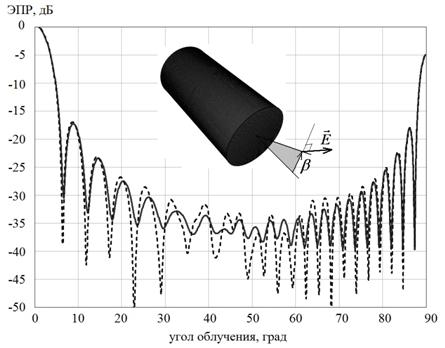
(б) – горизонтальная поляризация
Рис. 6. Зависимости ЭПР импедансного цилиндра от угла облучения (сплошная кривая – цифровое моделирование на основе полигональной модели по методу ФТД, штриховая кривая – расчет в программе EMSS FEKO)
Литература
1. Борзов А.Б., Быстров Р.П., Засовин Э.А., и др. Миллиметровая радиолокация: методы обнаружения и наведения в условиях естественных и организованных помех. – М.: Радиотехника, 2010, 376 с.
2. Уфимцев П.Я. Основы физической теории дифракции. – М.: Бином, 2009, 352 с.
3. Астанин Л. Ю., Костылев А. А. Основы сверхширокополосных радиолокационных измерений. – М.: Радио и связь, 1989, 192 с.
4. Антифеев В.Н., Борзов А.Б., Сучков В.Б. Физические модели радиолокационных полей рассеяния объектов сложной формы: учебное пособие. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2003, 63 с.
5. Нотт Ю.Ф., Сеньор Т.Б.А. Сравнение трех методов, применяемых в высокочастотной теории дифракции // ТИИЭР, 1974, Т.62, №11, с. 63-71.
6. Ахияров В.В. Решение задачи дифракции на импедансном клине // Электромагнитные волны и электронные системы, 2008, т.13, №11, с. 19-27.
7. Osipov A.V., Norris A.N. The Malyuzhinets theory for scattering from wedge boundaries: a review // Wave Motion, 1999, vol. 29, pp. 313-340.
8. Нефедов Е. И. Дифракция электромагнитных волн на диэлектрических структурах. – М.: Наука, 1979, 272 с.