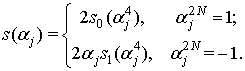УДК 621.391

СИНТЕЗ ЧЕРЕДУЮЩИХСЯ ТРОИЧНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ С ХОРОШИМИ АВТОКОРРЕЛЯЦИОННЫМИ СВОЙСТВАМИ И ВЫСОКОЙ ЭКВИВАЛЕНТНОЙ ЛИНЕЙНОЙ СЛОЖНОСТЬЮ

 

В. А. Едемский

Новгородский государственный университет им. Ярослава Мудрого

 

Статья получена 13 января 2014 г.

 

Аннотация. Предложен метод синтеза чередующихся троичных последовательностей, позволяющий получать последовательности с хорошими периодическими автокорреляционными свойствами и высокой эквивалентной линейной сложностью.

Ключевые слова: троичные последовательности, синтез, автокорреляция, линейная сложность.

Abstract: We propose the technique of synthesizing interleaved ternary sequences with low autocorrelation and high linear complexity.

Key words: ternary sequences, synthesis, autocorrelation, linear complexity.

 

Введение

Троичные периодические последовательности , где  N – период последовательности, наряду с бинарными относятся к одному из наиболее востребованных видов последовательностей [1, 2]. Для многих приложений важными характеристиками троичной последовательности (ТП) являются её периодическая автокорреляционная функция (ПАКФ)  и эквивалентная линейная сложность (ЭЛС). ЭЛС последовательности  над конечным полем третьего порядка  определяется как наименьшее натуральное число , для которого существуют константы  из  такие, что выполняется рекуррентное соотношение

 для всех  [3].

Последовательности, обладающие высокой ЭЛС , важны для криптографических приложений.

На настоящее время известны регулярные правила кодирования ТП с нечетным периодом  и идеальной ПАКФ , максимально возможной ЭЛС, равной [2,4,5]. В то же время ТП с периодом 4N и идеальной ПАКФ можно получить посредством произведения бинарной последовательности длинны 4 и ТП с периодом N [2].

В настоящей статье предлагается другой метод синтеза ТП с периодом 4N, обладающих идеальной ПАКФ и высокой ЭЛС. Метод основан на подходе, предложенном в [6], для синтеза бинарных последовательностей с периодом 4N и оптимальной ПАКФ .

 

2. Определение последовательностей

Пусть - последовательности с периодом  и матрица  порядка  образована размещением последовательностей  в её 1, 2, 3 и 4 столбцах соответственно. Тогда чередующая последовательность  периода  получается путем последовательного объединения строк матрицы  и обозначается , где  - оператор чередования. Таким образом, .

Обозначим через  наименьший положительный вычет  по модулю 4, а через  - целую часть рационального числа , тогда, согласно определению последовательности , получаем:

.                                               (1)

 

3. ПАКФ последовательностей

Пусть  и - ПАКФ последовательности , , а 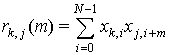 - периодическая взаимно корреляционная функция пары последовательностей , , здесь . Тогда, из (1) следует, что для ПАКФ  последовательности  справедливо соотношение [7]:

                  (2)

где  если  и  при

Обозначим через  оператор циклического сдвига последовательности на единицу влево.

Лемма 1. Если  - ТП, то:

1.  для любых целых значений  и ;

2. .

Доказательство. Первое утверждение леммы 1 хорошо известно (впрочем, оно является частным случаем второго). Во втором же случае согласно определениям периодической взаимно корреляционной функции и оператора  получаем

.

Лемма 1 доказана

Теорема 1. Пусть  - нечетное число и . Если ТП  имеют одинаковое число ненулевых элементов и

                                         (3)

то

Доказательство. Рассмотрим несколько случаев.

1. Пусть  Тогда, по лемме 1 и (2), получаем , где .

2. Пусть  В этом случае по лемме 1 имеем

.

Так как , то и .

3. Пусть  Здесь

или

.

При этом если , то , так как по условию .

4. Если , то, как и в первом подпункте, получаем, что .

Теорема 1 доказана.

Следствие 1.1. Если ТП  и  имеют идеальную ПАКФ, то последовательность  также имеет идеальную ПАКФ.

Следствие 1.2. Если ТП  имеет идеальную ПАКФ, то для любого целого  последовательность  также имеет идеальную ПАКФ.

Таким образом, правило кодирования (3) позволяет синтезировать семейства ТП с идеальными, а также квазиидельными периодическими автокорреляционными свойствами.

Пример 1. Пусть  и    - ТП с идеальной ПАКФ. Первая построенна на основе разностного множества Зингера [1, 2], а вторая с помощью множества биквадратичных вычетов и нуля [1].

Тогда

имеет идеальную ПАКФ, что несложно проверить непосредственным вычислением. Варьируя последовательности  и  получаем другие ТП с идеальной ПАКФ.

4. Эквивалентная линейная сложность последовательностей

Если  - последовательность с периодом , то её ЭЛС  можно вычислить по следующей формуле [3]:

                                 (4)

где - производящая функция цикла последовательности.

Пусть , в свою очередь, соответствует последовательности  с периодом .

Следующие утверждения доказаны в [8] для бинарых последовательностей, для ТП доказательства аналогичны.

 Лемма 2.

1. Если , то .

2. Если , где  - целое число, то

Лемма 3. Если  где, как и ранее,  для нечетного значения , то

Доказательство. По условию  и , тогда, в силу второго утверждения леммы 2,  и . Подставляя выражения для  в формулу для вычисления из первого пункта леммы 2, завершаем доказательство леммы 3.

Теорема 2. Пусть, соответственно,  - ЭЛС ТП  над полем третьего порядка, а  - последовательности  и . Тогда, если  то .

Доказательство. Пусть  - расширение поля , являющееся полем разложения многочлена  (оно всегда существует [3]). Обозначим через  различные корни многочлена  в поле . Тогда  и . Следовательно, по (4) имеем

                                              (5)

Согласно лемме 3  или

                                         (6)

Формула (5) приведена для ТП , подобные же соотношения имеют место и для ТП . Поэтому, в силу условия теоремы 2, имеем

 и .

А так как

; ,

то, из (6) получаем: . Применение (5) завершает доказательство теоремы 2.

Следствие 2.1. Если , то .

Таким образом, если ТП  имеют высокую ЭЛС, то и ТП , определяемая (3), также имеет высокую ЭЛС. Формулу (6) можно применять для поиска минимального многочлена  ТП  [6]. Заметим, что для последовательностей, расмотренных в примере 1, , здесь ТП  не обладает высокой ЭЛС.

 

Вывод

Предложен новый метод синтеза чередующихся троичных последовательностей с идеальными (квазиидеальными) автокорреляционными свойствами, высокой эквивалентной линейной сложностью и периодом .

Литература

1. Винокуров В.И., Гантмахер В.Е. Дискретно-кодированные последовательности. Ростов-на-Дону: Ростовский ун-т, 1990. 283 с.

2. Ипатов, В.П. Периодические дискретные сигналы с оптимальными корреляционными свойствами. М.: Радио и связь, 1992. 152 с.

3. Лидл Р., Нидеррайтер Г. Конечные поля. М.: Мир, 1988. 820 с.

4. Ипатов В.П. Троичные последовательности с идеальными периодическими автокорреляционными свойствами // Радиотехника и электроника. 1979. № 10. С. 2053–2057.

5. Ипатов В. П., Камалетдинов Б.Ж. Эквивалентная линейная сложность троичных последовательностей с идеальными автокорреляционными свойствами // Радиотехника и электроника. 1989. Т. 34, № 11. С. 2451–2454.

6. Tang X. H., Ding C. New classes of balanced quaternary and almost balanced binary sequences with optimal autocorrelation value // IEEE Trans. Inf. Theory. 2010. V. 56, № 12, pp. 6398–6405.

7. Едемский В. А., Гантмахер В. Е. Синтез двоичных и троичных последовательностей с заданными ограничениями на их характеристики. Великий Новгород.: НовГУ, 2009. 189 с.

8. Wang Q., Du X. N. The linear complexity of binary sequences with optimal autocorrelation // IEEE Trans. Inf. Theory. 2010. V. 56, № 12, pp. 6388–6397.