УДК 538.566.2

О ФАЗОВОЙ СКОРОСТИ ПОВЕРХНОСТНЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

 

В. Н. Дацко

Национальный исследовательский университет МИЭТ

Статья получена 20 февраля 2014 г.

Аннотация.   В опыте на сверхвысоких частотах  наблюдалась поверхностная электромагнитная  волна, фазовая скорость которой, в зависимости от величины поверхностного импеданса подстилающей поверхности, представляющей собой слой солёной воды на металле, принимала значения как меньше, так и больше  скорости света в вакууме; при этом скорость переноса энергии («энергетическая скорость») оставалась  меньше скорости света. Продемонстрирован резонаторный метод разделения поверхностных и пространственных электромагнитных волн.

Ключевые слова: поверхностная, пространственная волна, разделение  волн,   резонаторный метод, фазовая, энергетическая скорость волны, поверхностный импеданс, солёная вода.

Abstract.  In the experience of  the superhigh  frequencies observed surface electromagnetic wave phase velocity which, depending on the size of the surface impedance of the underlying surface ( a layer of salt water on the metal), has value as a smaller and more of the speed of light in a vacuum; the rate of energy transfer («energy rate») was less than the speed of light. Demonstrated cavity surface and spatial separation method of electromagnetic waves.

Keywords: surface and spatial waves, wave  split cavity method, phase speed and «energy speed» of the wave, the surface impedance, salty water.

 

Существование и свойства поверхностных электромагнитных волн (ПЭВ) следуют из уравнений Максвелла с соответствующими граничными условиями [1,2]. Волны  могут распространяться по поверхности раздела двух сред в том случае, если диэлектрическая проницаемость ε одной из них отрицательна (мода Фано [3]), либо имеет большую мнимую часть (мода Ценника [2]). Фазовая скорость моды Фано заметно меньше скорости света, что облегчает их наблюдение методом НПВО, с помощью дифракционной решётки, нанесённой на поверхность, или же методом нанолокализованных источников света в газоразрядной плазме (поверхностные плазмоны), в полупроводниках и металлах (поверхностные плазмон-поляритоны) в оптическом и терагерцовом диапазонах; с ними связывают большие надежды в области нанотехнологий.

 В отличие от моды Фано, фазовая скорость волны Ценника больше скорости света в вакууме, что делает непригодными упомянутые методы, поскольку моды Ценника совпадают по скорости с объёмными модами поверхностного волновода и «теряются» среди них. По этой причине до 1980г. волны Ценника экспериментально не наблюдались [4,5]. До сих пор существует предубеждение, что их вообще невозможно возбудить реальными антеннами, т.е. это волна-призрак, математический фокус, не имеющий физического смысла [8], поскольку скорость переноса энергии («энергетическая скорость») у них больше скорости света в вакууме, что противоречит основам физики.  По этому поводу возникла дискуссия в печати [6,7,8]. В нашем  эксперименте измерялась фазовая скорость ПЭВ и наблюдался переход её через скорость света.

Экспериментальный метод

Любой источник, расположенный вблизи поверхности раздела двух сред, возбуждает смешанное поле, состоящее из поверхностных и объёмных волн. Разделение волн – сложная  задача, которую мы решили, используя резонаторный метод. Идея использования замкнутого резонатора для разделения волн заключается  в том, что, благодаря ограниченности размеров резонатора по высоте, можно сделать скорость гармоник объёмного поля большей, чем скорость волны поверхностной, и осуществить тем самым их разделение либо по длине волны, либо по частоте. При этом поверхностная волна наблюдается в резонаторе в «чистом» виде, т.к. резонансы поверхностной и объёмной волн заметно разнесены по частоте и не перекрываются.

 

Схема эксперимента

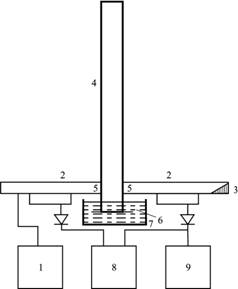
Рис.1. Схема эксперимента: 1– генератор СВЧ, 2 – волноводный тракт, 3 – согласованная нагрузка, 4 – резонатор, 5 – окна связи, 6 – металлическое дно резонатора, 7– кювета с солёной водой, 8 – индикаторный блок, 9 – измерительный усилитель.

 

Резонатор представлял собой прямоугольную трубу с металлическим дном и металлической крышкой (рис.1), его размеры: 4,7x6,2х50см³; в металлическом дне резонатора имелось отверстие для напуска воды в резонатор. Нижний конец резонатора был погружён в кювету с водой (солёность 40‰, что соответствует диэлектрической проницаемости 72+55i); уровень воды в нём изменялся путём постепенного удаления небольших количеств воды из кюветы. При изменении толщины слоя воды на металле менялся и импеданс поверхности. Резонатор был включён в волноводный тракт панорамного измерителя ослабления Р2-57, связь резонатора с трактом осуществлялась через окна связи, прорезанные в нижней части широких стенок резонатора и представлявшие собой горизонтальные щели шириной 0.З см и длиной 0.5 см. Сигнал, прошедший резонатор, детектировался и регистрировался измерителем ослабления (индикаторный блок) и селективным усилителем У2-8. Такой состав аппаратуры давал возможность контролировать амплитудно-частотную характеристику резонатора (рис.3-6), визуально наблюдать резонанс поверхностной волны и измерять его добротность и резонансную частоту.

Физика явления

Суть  процесса поясняет рис.1. Из волноводного тракта (2) через окно связи (5) волна попадает внутрь резонатора (4), в котором,  вследствие интерференция падающей и отражённой волн, образуются стоячие волны. Энергия поля сосредоточена вблизи пучностей, а узлы разделяют участки, несущие кванты энергии. Длина участка равна половине длины волны – происходит размерное квантование. Поле пространственной волны заполняет весь объём резонатора, и стоячие волны образуются в  плоскости поверхности и по вертикали – поле квантуется по трём координатам. Поле поверхностной волны, сконцентрированное вблизи поверхности, «не достаёт»  до верхнего края  резонатора и квантуется только «внизу» –  в плоскости поверхности. Если внутри резонатора укладывается целое число полуволн (порций энергии), то резонатор пропускает мощность (резонанс). На АЧХ возникает пик прохождения. При этом различные  условия квантования приводят к разделению поверхностной и объёмной волн  в резонаторе.

Резонатор-сепаратор

В  работе [9] рассмотрен прямоугольный резонатор поверхностной волны с поперечными размерами «a», «b» и высотой L, найдена его передаточная функция и показано, что ПЭВ будет резонировать  на частотах

 ,            (1)

где z_s-поверхностный импеданс, n и m =1,2...-целые числа, определяющие номер гармоники резонанса. Этот же резонатор, очевидно, будет иметь и резонансы, соответствующие объёмным волнам; их частоты определяются соотношениями

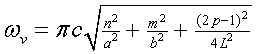.          (2)

Последний член под корнем в (2) указывает, что, поскольку верхний конец резонатора открыт, вдоль него по вертикали устанавливается (2р-1)/4 длин волн. Отсутствие в формуле (1) под корнем слагаемого вида (2р-1)² /4L² свидетельствует о том, что резонансы поверхностной волны разнесены по частоте с резонансами объёмных волн, что упрощает их отделение.  Резонанс поверхностной волны будет отделён от резонансов собственных объёмных мод резонатора, если выполняется условие

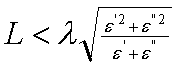
где l – длина волны в свободном пространстве и e = e^’ + ie^² – диэлектрическая проницаемость солёной воды.

Положение резонанса и его добротность весьма чувствительны к фазовой скорости и затуханию поверхностной волны, что позволяет сравнительно легко измерять зависимость их от импеданса поверхности.  Частота резонанса

 (1 +  )  ,              (3)

где  R и X – действительная и мнимая части поверхностного импеданса трёхслойной структуры металл-вода-воздух (рис.1), a и b – длина и ширина резонатора.

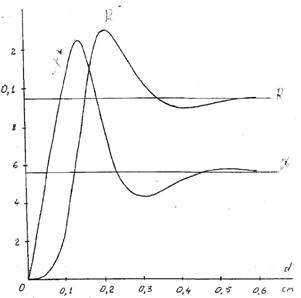
Рис.2.  Изменение эффективного импеданса поверхности воды в зависимости от толщины слоя воды на металле (солёность s = 80‰)  [10].

Фазовая скорость поверхностной волны  определяется формулой

v_p = с (1 + )                        (4)

R и X, в свою очередь,  определяются  формулами, приведёнными в [9]. Отсюда следует, что, измеряя в эксперименте частоту  резонанса, можно определить фазовую скорость

 (1 +  )= v_p                 (5)

где   - частота резонанса поверхностной волны;  a, b - длина и ширина резонатора,  R и X – действительная и мнимая части поверхностного импеданса трёхслойной структуры металл-вода-воздух.

Результаты

На рис.3 приведена амплитудно-частотная характеристика резонатора. Первый пик соответствует поверхностной волне, остальные – объёмным модам резонатора.

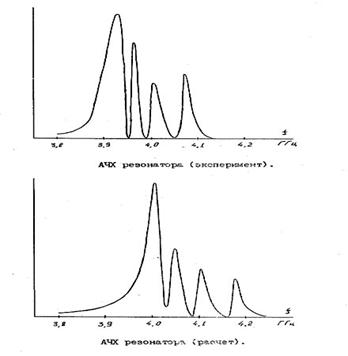
Рис.3. Амплитудно-частотная характеристика резонатора. Верхняя   часть – эксперимент, нижняя – расчёт. Первый пик соответствует поверхностной волне, остальные – объёмным модам резонатора.

Для доказательства возбуждения ПЭВ и пространственных мод снимались распределения поля по высоте для всех наблюдавшихся пиков. Результаты представлены на рис.4-6.

Рис.4.  Вертикальная структура в первом пике АЧХ. Сплошная кривая – расчёт.

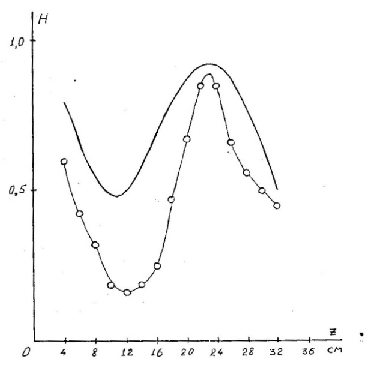
Рис.5   Вертикальная структура поля во втором пике АЧХ. Сплошная кривая – расчёт.

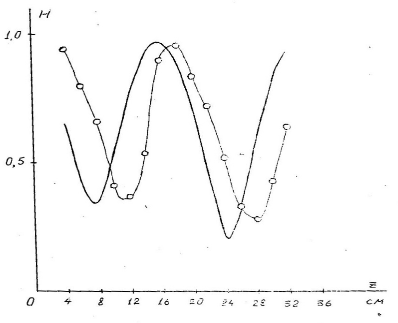
Рис.6  Вертикальная структура поля в третьем пике АЧХ. Сплошная кривая – расчёт.

 

Для доказательства поверхностного характера волны на рис.4 приведена вертикальная структура в первом пике, соответствующая экспоненциальному спаду поля волны при удалении от поверхности; на рис.5 и рис.6 – вертикальная структура поля во втором и третьем пиках.

На рис.7 приведён экспериментальный график зависимости фазовой скорости поверхностной волны от толщины слоя воды на металле и соответствующий теоретический расчёт (диэлектрическая проницаемость ε=72+55i.) Расхождение экспериментальных и теоретических кривых при малых толщинах связано с неравномерностью толщины слоя воды. Из графика видно, что максимальная скорость приходится на толщину приблизительно 0.2 см.

 

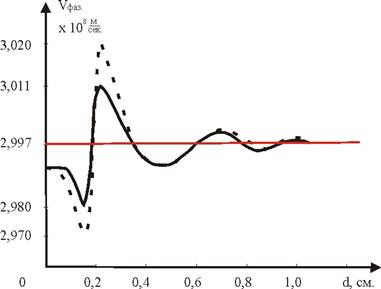
Рис.7  Зависимость фазовой скорости поверхностной волны от толщины слоя воды на металле. Сплошная кривая – эксперимент, штриховая – расчёт.

Обсуждение результатов

По формуле (3) найдём фазовую скорость волны (резонансная частота 4,0 ГГц) при толщине слоя воды 0.2 см:

v_0,2 = (3,007 ± 0,005) х 10⁸ м/сек    -    эксперимент ,

v_0,2 = 3,015 х 10⁸ м/сек           -             теория ,

скорость света в вакууме    с = 2,997 х 10⁸ м/сек.

При малых толщинах слоя воды на металле (0… 0.2 см) поверхностная волна в резонаторе является модой Фано, поскольку при этих толщинах мнимая часть эффективного импеданса поверхности превосходит его действительную часть (рис.2), т.к. в эксперименте наблюдался непрерывный переход от моды Фано к моде Ценника. Интересно отметить, что в данном случае, как показал В.В.Шевченко [13], понятие групповой скорости теряет смысл и неправомерно говорить о равенстве энергетической и групповой скоростей. Скорость переноса энергии – «энергетическая скорость» – меньше скорости света в вакууме, что проверяется непосредственным расчётом по формуле Умова-Пойнтинга

S = w v_e

(S–плотность потока энергии; w – плотность энергии; v_e – скорость переноса энергии).

В нашем случае при толщине слоя воды 0.2 см:

по теории фазовая скорость   v_p = 3.01 х10⁸ м/сек ,

энергетическая скорость   v_e = 2.986х10⁸ м/сек  c;

эксперимент - фазовая скорость   v_0,2 = (3,007 ± 0,005) х 10⁸ м/сек > c,

энергетическая  скорость    v_e = 2.996х10⁸ м/сек  c.

Эксперимент не противоречит теории [11,12,13]:      v_e c v_p .

Заключение

Поверхностные электромагнитные волны – классическая проблема радиофизики; они известны более ста лет. Однако,  в теории до сих пор нет единого мнения о возможности превышения фазовой скоростью волны скорости света в вакууме. Для экспериментальной  проверки необходимо умение разделять поверхностные и пространственные волны, возбуждённые источником, расположенным  на границе раздела сред – сложная  задача, не решённая до настоящего времени. По этой причине окончились неудачей все натурные эксперименты по обнаружению ПЭВ Ценника, проведённые в прошлом веке. Задачу удалось решить в лаборатории, применяя резонаторный метод. Поверхностные волны были выделены из смешанного поля, и наблюдался переход фазовой скорости волны через скорость света в вакууме. Полученный результат ставит точку в  споре о реальности ПЭВ Ценника.

 

Литература

1. Sommerfeld A. //  Annalen der Physik. 1899. V. 303. № 2. P. 233.

2. Zenneck J. // Annalen der Physik. 1907. V. 328. №10. P. 846.

3. Fano U. // J. Opt.Soc. Amer. 1941. V. 31. № 3. P. 213.

4. Байбаков В.И., Дацко В.Н., Кистович Ю.В. // Письма в ЖТФ. 1980. Т. 6. № 7. С. 394.

5. Байбаков В. И., Дацко В. Н., Кистович Ю. В. // Успехи физ. наук. 1989. Т. 157. № 4. С. 722.

6. Кукушкин А.В. // Успехи физ.наук. 2009. Т. 157. № 4. С. 801.

7. Дацко В.Н., Копылов А.А. // Успехи физ. наук. 2008. Т. 178.  № 2. С. 109.

8. Кукушкин А.В., Рухадзе А.А., Рухадзе К.А. //  Успехи физ.наук. 2012. Т. 182. № 11. С. 1205.

9. Байбаков В.И., Кистович Ю.В. // Журнал технической физики. 1982. Т. 52. № 5. С. 846.

10. Кистович Ю.В.  Поверхностные электромагнитные волны Ценника СВЧ диапазона на солёной воде. Дисс. ... кандидата физ-мат.наук. М. : ВНИИ-ФТРИ. 1987. 120 с.

11. Шевченко В.В. Плавные переходы в открытых волноводах М. : Наука. 1969.

12. Вайнштейн Л.А Электромагнитные волны. М. : Радио и связь. 1988. С. 244.

13. Шевченко В.В. // Журнал радиоэлектроники [электронный журнал].  2013.  № 7.  URL: http://jre.cplire.ru/jre/jul13/7/text.pdf