СВЧ свойства неравновесных джозефсоновских контактов
в субмикронных и слоистых сверхпроводниках
Д.А. Рындык,
Институт физики микроструктур РАН, Нижний
Новгород
Получена
20 января 2000 г.
В работе рассматриваются некоторые СВЧ свойства неравновесных джозефсоновских
контактов в субмикронных и слоистых сверхпроводниках. В отличии от обычного
эффекта Джозефсона, при неравновесном эффекте необходимо самосогласованным
образом описывать динамику квазичастиц и джозефсоновских фаз. Возникающее
в результате взаимодействие между контактами существенно влияет на их СВЧ
свойства. В работе проанализирована динамика цепочки одинаковых контактов,
в том числе при внешнем СВЧ воздействии (ступеньки Шапиро), а также рассмотрена
динамика системы двух контактов с существенно разными параметрами, где
имеет место эффект усиления джозефсоновских осцилляций.
Введение
Эффект Джозефсона - один из самых ярких макроскопических квантовых эффектов,
был теоретически предсказан Брайаном Джозефсоном (B.D. Josephson) в 1962
году [1] и вскоре экспериментально обнаружен
[2]. Предсказание и экспериментальное открытие
этого эффекта оказали существенное влияние на развитие фундаментальных
представлений о макроскопических квантовых системах и, в то же время, привели
к широким и неожиданным перспективам практического применения сверхпроводников.
В настоящее время существует обширная литература как по физическим основам,
так и по практическим применениям эффекта Джозефсона. В частности, пять
монографий на русском языке [3,4,5,6,7]
и большое число обзоров.
Обычно под эффектом Джозефсона понимают совокупность явлений при протекании
электрического тока через слабую связь между двумя массивными сверхпроводниками
(термин "слабая сверхпроводимость" введен Андерсоном (P.W. Anderson) в
1964 году). Примерами таких связей являются: туннельный переход, узкий
сверхпроводящий мостик (мостик Дайема), S-N-S контакт (сверхпроводник -
нормальный металл - сверхпроводник), точечный контакт и др. В последнее
время большое внимание привлек так называемый внутренний (intrinsic) эффект
Джозефсона в сильноанизотропных высокотемпературных сверхпроводниках (типа
Bi2Sr2CaCu2O8+d,
Tl2Ba2Ca2Cu3O10+d
и др.). Эти соединения имееют слоистую структуру и джозефсоновская связь
осуществляется между сверхпроводящими слоями CuO2.
С момента открытия в 1962 году эффект Джозефсона является актуальной
темой фундаментальных и прикладных исследований по сверхпроводимости. С
точки зрения фундаментальной физики он весьма ярко проявляет отличия сверхпроводящего
состояния электронной жидкости в металлах от нормального. Так, совершенно
иначе выглядит туннельный эффект. Именно решая задачу о протекании электрического
тока между двумя сверхпроводниками, разделенными тонким слоем изолятора,
Б. Джозефсон обнаружил два удивительных факта. Во-первых, постоянный ток,
меньший некоторого критического тока Jc, протекает через туннельный
переход без сопротивления (туннельный сверхток)
Это явление (удивительное в туннельных и S-N-S структурах) получило специальное
название стационарный эффект Джозефсона. Во-вторых, при J > Jc
напряжение на переходе не является постоянным, а осциллирует с периодом
T = 2p/wJ
где wJ-"джозефсоновская частота"
связана со средним напряжением на переходе < V >
-
2e < V > = (h/2p)wJ
при J > Jc .
Заметим, что в это макроскопическое соотношение входит постоянная Планка
(h/2p), что указывает
на принципиально квантовый характер эффекта, получившего название нестационарный
эффект Джозефсона.
С самого начала стало ясно что как стационарный, так и нестационарный
эффекты имеют большую область практических применений. На стационарном
эффекте, например, основаны сверхчувствительные (до 10-9 Гс)
измерители магнитного поля. Использование нестационарного эффекта (в различных
СВЧ системах) привлекательно вследствие весьма большой характерной частоты
джозефсоновской генерации fJ = wJ
/2p, отношение между которой и приложенным напряжением
равно
так что при характерных напряжениях V = 10-6ё10-3
В, fJ = 109ё1012
Гц, а в ВТСП до 10 ТГц. Фундаментальным ограничением на fJ является
величина энергетической щели, лежащая в инфракрасном диапазоне. Таким образом
джозефсоновская генерация покрывает весьма важный субмиллиметровый диапазон
частот.
Естественным препятствием, однако, является малая мощность излучения
одного контакта. Как показано в ряде работ (см. напр. [7],
стр. 216) максимальная мощность излучения одного контакта во внешнюю электродинамическую
систему Pmax определяется соотношением
где RN - нормальное сопротивление контакта при данной температуре
(RN при T < Tc может быть определенно путем подавления
сверхпроводимости, например магнитным полем). При типичных значениях параметров
Vc = RN Jc ~ 10-3
В, Jc ~ 10-3 А эта мощность
имеет порядок 10-7 Вт.
Другой сложностью является согласование импедансов перехода и внешней
системы. Максимальная мощность (2) достигается только
при импедансе контакта Z порядка импеданса внешней волноведущей системы
Ze (согласование импедансов), но Z как правило не превосходит
нормального сопротивления контакта RN, которое имеет порядок
1 Ома, в то время как типичное значение |Ze|
составляет 50-100 Ом. В результате реально измеряемая мощность излучения
одного контакта составляет @ 10-9ё10-8
Вт, что недостаточно для практических применений.
Обе вышеназванные проблемы можно решить, если использовать системы
джозефсоновских контактов. Комбинируя параллельно и последовательно
соединенные переходы можно подобрать импеданс равный внешнему. Увеличивается
и максимальная мощность излучения. Кроме того, происходит сужение линии
генерации. При этом, однако, необходимо чтобы все контакты работали когерентно.
Один из возможных путей - синхронизация собственным СВЧ полем. Взаимна
синхронизация и захват фазы (mutual phase locking) в системах джозефсоновских
контактов при высокочастотном электромагнитном взаимодействии были предметом
многочисленных теоретических и экспериментальных исследований (см. обзор
[8]). Оказалось что синхронизация
в таких системах принципиально возможна, но трудно достижима при наличии
разброса параметров в реальных джозефсоновских структурах. Тем не менее,
недавно в системе из 2000 джозефсоновских контактов, встроенных в полосковую
линию, была получена рекордная для сверхпроводящих систем мощность излучения
160 мкВт на частоте 240 ГГц [9]. Оценки
показывают, что в таких системах можно получить мощность порядка 1 мВт
при ширине линии 100-500 кГц.
Другой возможностью является использование длинного перехода Джозефсона
(т.н. Flux Flow генератор на джозефсоновских вихрях), где излучают джозефсоновские
вихри, периодически выходящие из края перехода под действием внешнего тока.
В настоящее время сделаны Flux Flow генераторы, работающие в диапазоне
100-700 ГГц, с мощностью ~ 1 мкВт и шириной
линии 100 кГц - 1 МГц в зависимости от частоты [10].
Использование системы фазовой автоподстройки частоты позволяет существенно
уменьшить ширину линии генерации.
Все рассмотренные выше схемы имеют дело с "обычными" джозефсоновскими
контактами, расстояния между которыми составляют десятки и сотни микрон.
Характерной особенностью обычного эффекта Джозефсона является то обстоятельство,
что все нетривиальные процессы протекают только в самой слабой связи, состояние
же массивных сверхпроводников (берегов) остается равновесным. В этом предположении
строится и стандартная теория слабой сверхпроводимости. В то же время,
хорошо известно, что джозефсоновский контакт при ненулевом напряжении является
источником нетепловых квазичастиц, которые релаксируют в берегах. Поэтому
вблизи контакта всегда возникает область неравновесной сверхпроводимости.
Избыточные квазичастицы вызывают изменение энергетической щели. Кроме того,
возникает разность населенностей электронноподобной и дырочноподобной ветвей
спектра элементарных возбуждений (электронно-дырочный разбаланс), что приводит
к изменению химического потенциала сверхпроводящего конденсата (число сверхпроводящих
электронов меняется, чтобы скомпенсировать избыточный заряд квазичастиц)
и проникновению электрического поля в сверхпроводник (см. обзоры [11,12,13]).
Если размер берегов достаточно велик, то основную роль играет диффузия квазичастиц
(в грязных сверхпроводниках). Характерные пространственные масштабы определяются
длиной энергетической релаксации le
= Ц{Dte}
и длиной релаксации разбаланса (глубиной проникновения электрического поля)
lq = Ц{Dtq},
D - коэффициент диффузии, te - врем
неупругой релаксации, tq - врем релаксации
разбаланса. Если же размер берегов в направлении диффузии мал, то образуется
пространственно однородное неравновесное состояние, релаксирующее с характерными
временами te и tq.
В этом случае степень неравновесности может быть значительно больше.
Эффекты квазичастичного взаимодействия между контактами исследовались
ранее в системах мостиков Мерсеро-Нотариса [14,15]
и в S-N-S контактах [16,17].
В последнее время активно исследуются одномерные и двумерные системы туннельных
S-I-S джозефсоновских контактов, а также многослойные структуры с характерными
размерами (толщинами слоев) порядка микрона и меньше. Для этих структур
нет оснований полагать, что неравновесные эффекты малы. Напротив, можно
ожидать существования новых интересных явлений. Один из таких эффектов,
исследованный ранее, - это неравновесное изменение энергетической щели
в S-I-S структурах, интересным частным случаем которого является стимулирование
(усиление) сверхпроводимости в двойном туннельном контакте с неравновесным
средним слоем [18,19,20,21].
Еще более важную роль может играть нарушение джозефсоновского соотношения
(dj/dt) = (2e/(h/2p))V
между напряжением и разностью фаз на контакте в неравновесном случае (см.
ниже). В слоистых сверхпроводниках с джозефсоновской связью между слоями
неравновесные эффекты могут быть очень велики
вследствие малой (3-10 ?)
эффективной толщины слоев. В недавних работах [22,23,24,25,26,27,28,
29,30,31,32,33,34,35,36,37]
было проведено прямое наблюдение внутреннего эффекта Джозефсона в ВТСП.
В работах [38,39,40,41,42,43]
была отмечена необходимость учета неравновесных эффектов, и особенно нарушения
равновесного джозефсоновского соотношения, при интерпретации эксперимента.
В настоящей работе рассмотрены некоторые СВЧ свойства неравновесных
джозефсоновских контактов. В части 2 работы сформулирована простая система
уравнений теории неравновесного эффекта Джозефсона. В части 3 рассмотрена
синхронизация в цепочке контактов. В части 4 исследовано СВЧ воздействие
на цепочку (ступеньки Шапиро). В части 5 рассмотрен эффект неравновесного
усиления джозефсоновских колебаний в системе двух контактов с существенно
разными параметрами.
Неравновесный эффект Джозефсона
С микроскопической точки зрения основным процессом в неравновесном сверхпроводнике
является изменение функции распределения квазичастиц, которое сопровождается
изменением макроскопических характеристик конденсата: энергетической щели
D,
сдвига химпотенциала
dm и связанного с ним инвариантного
потенциала F.
Изменение энергетической щели происходит при изменении симметричной
по энергии части функции распределения ne
(ne при e
> 0 описывает распределение квазиэлектронов по энергиям, а ne
при e < 0 - квазидырок) и в простейшем случае
может быть найдено из уравнения самосогласования Элиашберга [44]
| 1 = l |
у
х |
qD
D |
|
1-ne-n-e
(e2-D2)1/2 |
de. |
|
(3) |
Сдвиг химического потенциала конденсата в сверхпроводнике, напротив,
определяется антисимметричной по энергии частью функции распределения
[45,46,47].
В простейшем случае чистого сверхпроводника в пространственно однородном
квазистатическом неравновесном состоянии распределение спаренных электронов
по энергии дается выражением vk2 = (1/2)(1-xk/ek),
где
xk = (h/2p)2k2/2m-eF-dm,
ek
= Ц{D2+xk2}
- спектр квазичастиц, dm - сдвиг химпотенциала.
Тогда плотность заряда при
dm << eF
определяется выражением
| r = 2eN(0) |
й
л |
dm+ |
у
х |
Ґ
D |
(ne-n-e)de |
щ
ы |
, |
|
(4) |
в котором первый член есть заряд конденсата, а второй - заряд квазичастиц,
N(0) = mpF/2p2(h/2p)3
- плотность состояний на поверхности Ферми. Уравнение (4)
является вторым уравнением самосогласования. В квазинейтральном случае
(r » 0) получаем
| dm = - |
у
х |
Ґ
D |
(ne-n-e)de. |
|
(5) |
Это выражение отражает особенность зарядовых эффектов в сверхпроводниках:
при возникновении электронно-дырочного разбаланса общая квазинейтральность
может быть соблюдена за счет сверхпроводящих электронов.
Сдвиг химпотенциала может быть выражен через так называемый инвариантный
потенциал: dm = -eF,
| F(t) = f+((h/2p)/2e)(¶q/¶t), |
|
(6) |
где f - электрический потенциал, q
- фаза параметра порядка, F = 0 в равновесном
состоянии. В чистом сверхпроводнике в квазиклассическом случае это соответствие
следует прямо из вида спектра квазичастиц [46].
В общем случае именно калибровочно инвариантный потенциал F
входит в динамические уравнения. Выражение для заряда принимает вид
| r = -2e2N(0)(F-Y)
= - |
1
4prd2 |
(F-Y), |
|
(7) |
где Y = 1/eтDҐ(ne-n-e)de
- потенциал электронно-дырочного разбаланса (oпределение потенциала Y
именно таким образом удобно при получении динамических уравнений), rd
- длина экранирования электрического поля.
В состоянии со сдвигом химпотенциала обычное соотношение (djij/dt)
= (2|e|/(h/2p))Vij
между джозефсоновской разностью фаз jij
= [qj-qi]signe
и напряжением Vij = fi-fj
нарушается. Вместо этого, используя определение F,
получаем неравновесное соотношение Джозефсона
|
djij
dt |
= |
2|e|
(h/2p) |
Vij+ |
2|e|
(h/2p) |
(Fj-Fi). |
|
(8) |
Таким образом, в общем случае необходимо самосогласованным образом описывать
динамику джозефсоновских фаз jij(t)
и функций распределения n(i)e(t)
с учетом условий (3), (7) и с
неравновесными выражениями для туннельного тока между берегами (слоями).
Основными параметрами, определяющими степень неравновесных эффектов
любого типа в туннельных структурах и других системах со слабыми связями,
являются произведения nte и ntq,
где n - так называемая туннельная частота, которая
при малой толщине слоя d0 << le,lq
равна
где RN - сопротивление контакта в нормальном состоянии на
единицу площади. Если nte > 1 или
ntq
> 1, то возможно сильное искажение фукнции распределения квазичастиц.
При малых напряжениях (V << D) относительное
изменение щели невелико, а взаимодействие (квазичастичное) джозефсоновских
контактов, связанное с разбалансом, определяется, в основном, параметром
h
= 2ntq f(T), где tq
при T ~ Tc может существенно превосходит
время энергетической релаксации te,
tq
= (4T/pD)te
>> te. Фактор f(T) описывает уменьшение
числа равновесных квазичастиц с температурой и для сверхпроводника с "хорошей
щелью" (сильной особенностью в плотности состояний) равен f(T) = 1-tanh(D/2T).
Следовательно при T ~ Tc: f(T) »
1, а при низких температурах разбаланс становиться экспоненциально малым.
Если, однако, особенность в плотности состояний размыта, то экспоненциальное
спадание эффекта с температурой уже не имеет места. Такое размытие происходит
в сверхпроводниках с магнитными примесями, в тонких слоях вследствии влияни
границы, а также при неизотропной в импульсном пространстве щели, что может
быть в ВТСП.
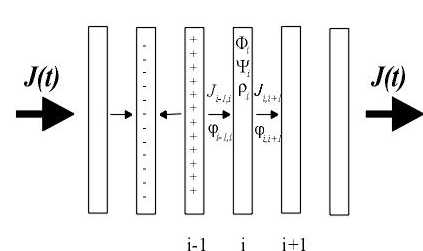
Рис. 1 Система джозефсоновски связанных тонких слоев.
В этой работе мы рассматриваем систему джозефсоновски связанных тонких
слоев (Рис. 1), с туннельным механизмом переноса тока между слоями. Таким
образом, состояние i-го слоя определяется его взаимодействием с i-1 и i+1
слоями. Будем считать, что толщина слоёв d0 сравнима с глубиной
экранирования электрического поля rd (что имеет место в ВТСП)
и много меньше характерных глубин релаксации неравновесности d0
<< le,lq. В этом
случае анализ зарядовых эффектов упрощается, так как можно провести усреднение
всех величин по толщине слоя.
Система уравнений для макроскопических величин: электронно-дырочного
разбаланса в слое Yi и тока между
слоями Ji-1,i была получена в [40,41,42,43]
и в простейшем случае имеет вид
| tqG |
dYi
dt |
+Yi = -2tqnRNJc(sinji-1,1-sinji,i+1), |
|
(10) |
| Ji-1,i = |
(h/2p)
2|e|RN |
|
dji-1,i
dt |
+ |
Yi-1-Yi
RN |
+Jcsinji-1,i, |
|
(11) |
где G - некоторый параметр, меньший единицы.
В выражении для тока первый член соответствует нормальному (квазичастичному)
току в равновесном случае, а второй - описывает неравновесную добавку к
нормальному току, третий член представляет собой обычное выражение дл сверхтока.
Используя эти уравнения, выведем полную систему динамических уравнений
для цепочки контактов. Следуя работам [38,39,42,48,49,50],
воспользуемся уравнением непрерывности
| d0 |
dri
dt |
= Ji-1,i-Ji,i+1, |
|
(12) |
и уравнением, связывающим напряжение (электрическое поле) между слоями
с зарядом слоев
| Vi,i+1-Vi-1,i = |
4pd0d
e0 |
ri, |
|
(13) |
здесь d - расстояние между слоями, e0
- диэлектрическая проницаемость. Из этих уравнений следует, что
| Ji-1,i+ |
e0
4pd |
|
dVi-1,i
dt |
= J(t), |
|
(14) |
J(t) - внешний ток. Эти уравнения совместно с неравновесным соотношением
Джозефсона (8), выражениями для заряда (7)
и тока (11), а также уравнением динамики разбаланса
(10) составляют полную систему динамических уравнений
цепочки контактов.
В безразмерном виде получаем
| b |
d2ji,i+1
dt2 |
+ |
dji,i+1
dt |
+sinji,i+1+yi-yi+1+b |
ж
з
и |
dmi
dt |
- |
dmi+1
dt |
ц
ч
ш |
= j(t), |
|
(15) |
| aG |
dyi
dt |
+yi = -h(sinji-1,i-sinji,i+1), |
|
(16) |
| mi+z(2mi-mi-1-mi+1)
= yi+z |
ж
з
и |
dji-1,i
dt |
- |
dji,i+1
dt |
ц
ч
ш |
, |
|
(17) |
где j(t) - внешний ток в единицах Jc, v(t) - внешнее напряжение
в единицах Vc = RNJc,
m(t)
= F(t)/Vc, y(t)
= Y(t)/Vc, и a
= tqwc,
b
= wc2/wp2,
z
= (e0 rd2)/(d0d),
wc
= (2eRNJc)/(h/2p),
wp2
= (8pedJc)/((h/2p)e0S),
t
= wc t,
h
= 2ntq. Отметим, что между коэффициентами
имеет место соотношение az = bh,
вытекающее из их определений.
Уравнения (15)-(18) являются
простейшим приближением, они справедливы вблизи критической температуры
или в бесщелевых сверхпроводниках. В более общем случае необходимо учитывать
т.н. интерференционные члены в выражении для тока и в уравнении динамики
электронно-дырочного разбаланса (см. [43]).
Эти члены, даже если они малы, могут существенно влиять на СВЧ взаимодействие
контактов. Ниже мы рассмотрим влияние интерференционного члена "f2" в уравнении
для разбаланса. Модифицированное уравнение имеет вид
| aG |
dyi
dt |
+yi = -h(sinji-1,i-sinji,i+1)-
hf2 |
ж
з
и |
dji-1,i
dt |
cosji-1,i- |
dji,i+1
dt |
cosji,i+1 |
ц
ч
ш |
. |
|
(19) |
Синхронизация в цепочке контактов
Теперь, пользуясь полученными выше уравнениями, обсудим характер высокочастотного
взаимодействия контактов. Этот вопрос важен как при интерпретации СВЧ эксперимента
по внутреннему эффекту Джозефсона в ВТСП, так и с прикладной точки зрения.
Особый интерес представляет режим синфазной синхронизации цепочки контактов,
в котором достигаются оптимальные условия для генерации и приема микроволн.
Наши исследования показали, что как при слабом (h
< 1), так и при сильном взаимодействии (h
> 1) могут иметь место как синфазные режимы , так и более сложные синхронные
режимы со сдвигом фаз, неоднородные режимы с разными ведущими частотами
контактов и хаотические режимы. При слабом взаимодействии, в режимах с
частью контактов в резистивном состоянии, наблюдалась синхронизация групп
контактов. Численные расчеты показали, что тип синхронизации зависит от
параметров и от внешнего тока. Так, например, при малых значениях
h
в рамках упрощенной системы уравнений (15)-(18)
наблюдается синфазная синхронизация, но дополнительный учет члена "f2"
, входящего в более общее уравнение (19), приводит
к более сложному режиму со сдвигом фаз (Рис. 2). Интересно также отметить,
что при больших параметрах h бывают режимы,
в которых синфазная синхронизация наблюдается только при некоторых значениях
тока, а в промежутках имеет место сдвиг фаз. При больших параметрах неравновесности
h
> 1 динамика системы еще более усложняется и режим синфазной синхронизации
наблюдается только при больших токах. Таким образом, из нашего анализа
следует, что квазичастичное взаимодействие, хотя и может быть использовано
для синхронизации контактов, однако это требует тщательного исследования
характера СВЧ взаимодействия, поскольку, в случае несинфазной синхронизации,
использование цепочки контактов для излучения или приема микроволн может
быть только затруднено.
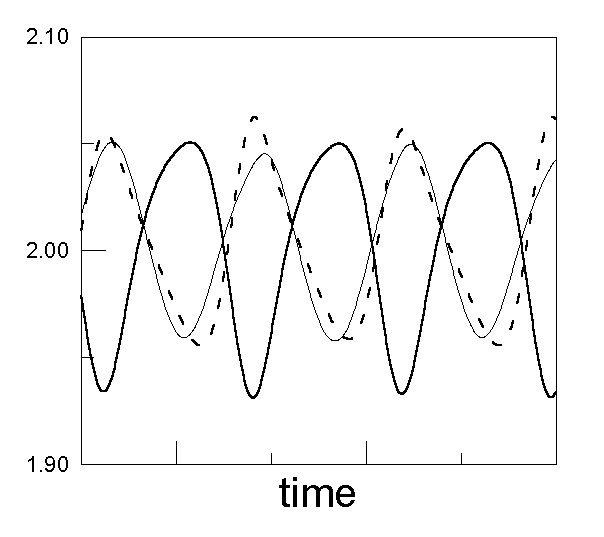
Рис. 2 Временная динамика джозефсоновских фаз (изображены dj1/dt,
dj2/dt и dj3/dt)
при
b = 10, aG =
0.1, h = 0.5, z =
1 и j = 2 с учетом интерференционного члена "f2" с f2 = 0.1 (режим со сдвигом
фаз).
Ступеньки Шапиро при внешнем СВЧ воздействии
Один из наиболее ярких эффектов - ступеньки напряженния на ВАХ, наблюдаетс
при СВЧ воздействии на переход и является простейшим примером синхронизации
внешним полем. Рассмотрим здесь эту задачу для одного перехода в рамках
высокочастотного
приближения. Будем считать, что на переход совместно действуют заданные
постоянный (I0) и переменный (Iwsin(wt))
токи. Тогда имеем уравнение
| b |
d2j
dt2 |
+ |
dj
d t |
+sinj = I0+Iwsin(wt). |
|
(20) |
Условием ВЧ предела является
В этом случае вкладом сверхтока в общий переменный ток можно пренебречь
и вычислить сначала быстро осциллирующую часть фазы (jw)
в линейном приближении, а потом вернуться к вычислению плавной части
W(t)
= < j(t) > , где символ < ... > обозначает
усреднение по "быстрым" временам ~ w-1.
Таким образом, решение для j имеет вид
где
|
| f = arctan |
ж
з
и |
1
bw |
ц
ч
ш |
, |
|
|
|
|
|
|
(23) |
Для определения W подставим (22)
в (20) и усредним по быстрым временам. В результате
получим укороченное уравнение
| b |
d2W
dt2 |
+ |
dW
d t |
+ < sin[W-Asin(wt
+f)] > = I0. |
|
(24) |
При слабом внешнем сигнале (A << 1) достаточно разложить sin в
ряд, тогда для < sinj > имеем
| < sinj > = < sinW
> - |
A
2 |
< sin(W+wt+f)
> + |
A
2 |
< sin(W-wt-f)
> . |
|
Отсюда видно, что взаимодействие носит резонансный характер и описывается
ненулевым третьим членом при dW/dt
~ w. При таком условии первые два члена равны нулю (усредняемые
функции быстро осциллируют) и в результате получим
| b |
d2W
dt2 |
+ |
dW
d t |
+ |
A
2 |
< sin(W-wt
-f) > = I0. |
|
(25) |
Введем новую переменную, которая имеет смысл фазовой расстройки перехода
по отношению к внешнему сигналу
Тогда уравнение (25) приобретает вид полностью
аналогичный исходному уравнению RSJ-модели с постоянным внешним током I0*
= I0-w и критическим током Ic*
= A/2
| b |
d2y
dt2 |
+ |
dy
d t |
+Ic*siny
= I0*. |
|
Свойства этого уравнения хорошо известны и анализ синхронизации можно провести
подробно. Мы ограничимся здесь констатацией факта, что в интервале внешних
токов
| DI = A = |
Iw
bw2cosf+wsinf |
|
|
с центром в точке I0 = w существует
синхронизованное внешним полем состояние с dW/dt
= wJ = w.
При b << 1 это состояние единственное,
а в общем случае имеет место гистерезис. Отметим, что в синхронизованном
состоянии при изменении тока через переход напряжение остается неизменным
(так как V µ dW/dt
= w), следовательно, на вольт - амперной характеристике
перехода образуется ступенька напряжения! Этот красивый резонансный эффект
был предсказан в первой работе Джозефсона и экспериментально обнаружен
Шапиро (S. Shapiro) и получил название ступенек Шапиро. В настоящее
время наличие ступенек Шапиро является самым верным признаком эффекта Джозефсона.
Проведенные нами численные расчеты вольт-амперных характеристик одномерных
цепочек неравновесных контактов показали, что результат СВЧ воздействи
существенно зависит от того, в каком динамическом состоянии находились
контакты без внешнего СВЧ тока. Для сравнения на Рис. 3 показаны ВАХ двух
цепочек 10 контактов с параметрами b = 10,
z
= 1 и разной степенью неравновесности: h = 0.1,
a
= 0.01 (показаны сплошной линией) и h = 1, a
= 1 (показаны пунктирной линией), при разном уровне переменного тока Iw
= 5, 20, 30. Видно, что в цепочке со слабой неравновесностью (h
= 0.1) ступеньки Шапиро формируются обычным образом. В случае же сильной
неравновесности (h = 1), при слабом вненшнем
воздействии ступеньки вовсе отсутствуют и начинают формироваться только
когда внешнее воздействие пересиливает взаимодействие между контактами.
 Рис. 3 ВАХ цепочки 10 контактов при внешнем СВЧ воздействии при
слабой (сплошная линия) и сильной (пунктирная линия) неравновесности.
Рис. 3 ВАХ цепочки 10 контактов при внешнем СВЧ воздействии при
слабой (сплошная линия) и сильной (пунктирная линия) неравновесности.
Неравновесное усиление джозефсоновских колебаний
Другой тип эффектов может наблюдаться в системах контактов с существенно
разными параметрами. Рассмотрим систему двух контактов с неравновесным
средним электродом в пределе z = 0 (пренебрегаем
влиянием заряда на сдвиг химпотенциала). Исходная система уравнений имеет
вид
|
|
dj1
dt |
= |
2e
(h/2p) |
V1+ |
2e
(h/2p) |
F, |
|
|
dj2
dt |
= |
2e
(h/2p) |
V2- |
2e
(h/2p) |
F, |
|
| Jcisinji
+ |
Vi
Ri |
+Ci |
dVi
dt |
= J(t), i = 1,2, |
|
| tqG |
dF
dt |
+F = -h1R1Jc1sinj1+h2R2Jc2sinj2. |
|
|
|
|
(26) |
Переходя к безразмерным переменным, будем считать, что характерные напряжения
контактов совпадают R1Jc1 = R2Jc2
= Vc. Это предположение вполне разумно, например, для туннельных
контактов, отличающихся прозрачностью барьера. Тогда получим
|
| b1 |
d2j1
dt2 |
+ |
dj1
dt |
+sinj1-m-b1 |
dm
dt |
= j1, |
|
| b2 |
d2j2
dt2 |
+ |
dj2
dt |
+sinj2+m+b2 |
dm
dt |
= j2, |
|
| aG |
dm
dt |
+m = -h1sinj1+h2sinj2 |
|
|
|
|
(27) |
| bi = |
2eJciRi2Ci
(h/2p) |
, a
= tqwc,
ji = |
J
Jci |
, |
|
| m(t) = |
2e
(h/2p)wc |
F(t), wc
= |
2eVc
(h/2p) |
, t
= wc t. |
|
Предположим теперь, что прозрачность (туннельная частота) второго барьера
значительно больше, чем первого n1
<< n2. Тогда критические токи
и параметры неравновесности контактов существенно различаются Jc1
<< Jc2, h1 <<
h2.
Рассмотрим область внешних токов больших, чем критический ток второго контакта.
Тогда j2 > 1 и j1 >> 1. Вкладом от члена h1sinj1
в уравнении для m можно пренебречь, и тогда
в простейшем случае aG << 1 и bw2
<< 1 получим
Из этого уравнения следует, что критический ток эффективно увеличилс
в 1+h2 раз и, соответственно, увеличится
амплитуда джозефсоновских осцилляций. В то же время высокочастотные джозефсоновские
осцилляции на первом контакте с частотами в j1/j2
раз большими, чем на втором контакте, можно не принимать во внимание.
Заключение
Использование неравновесных джозефсоновских контактов открывает новые возможности
для генерации и приема микроволн. Особенно перспективными являются искусственные
туннельные структуры с большой прозрачностью барьеров и
внутренние джозефсоновские
контакты в высокотемпературных сверхпроводниках.
Автор благодарит А.А. Андронова, В.В. Курина и А.С. Мельникова за поддержку
работы и плодотворные дискуссии. Работа выполнена при частичной поддержке
грантов РФФИ No. 97-02-16928, 99-02-16188 и 96-15-96591 ("Ведущие научные
школы"), а также при поддержке гранта INTAS No. 96-0457 и исследовательской
программы Международного центра фундаментальной физики в Москве (ICFPM).
References
-
[1]
-
B. D. Josephson. Phys. Lett., 1, 251-253, (1962).
-
[2]
-
P. W. Anderson and J. M. Rowell. Phys. Rev. Lett., 10, 230-232,
(1963).
-
[3]
-
И. О. Кулик и И. К. Янсон. Эффект Джозефсона в сверхпроводящих туннельных
структурах. М.: Наука, (1970).
-
[4]
-
Л. Солимар. Туннельный эффект в сверхпроводниках и его применение.
М.: Мир, (1974).
-
[5]
-
К.К. Лихарев, Введение в динамику джозефсоновских переходов. М.:
Наука, (1985).
-
[6]
-
А. Бароне, Дж. Патерно, Эффект Джозефсона , М.: Мир, (1984).
-
[7]
-
K. Лихарев, Б. Ульрих, Системы с джозефсоновскими контактами . M:
Наука, (1978).
-
[8]
-
A. K. Jain, K. K. Likharev, J. E. Lukens, and J. E. Sauvageau. Phys.
Rep, 109 (6), 309-426, (1984).
-
[9]
-
P.A.A. Booi, S.P. Benz, Appl. Phys. Lett. 68, 3799 (1996).
-
[10] V.P. Koshelets et al.,
Phys. Rev. B 56, 5572 (1997).
-
[11] С.Н. Артеменко, А.Ф.
Волков, УФН 128, 3 (1979).
-
[12] Nonequilibrium Superconductivity,
ed. D.N. Langenberg and A.I. Larkin, Modern Problems in Condensed Matter
Sciences Vol. 12 (North-Holland, Amsterdam, 1986).
-
[13] А.М. Гулян, Г.Ф. Жарков,
Сверхпроводники
во внешних полях, М.: Наука (1990).
-
[14] D.W. Palmer, J.E. Mercereau,
Phys.
Lett. A 61, 135 (1977).
-
[15] С.Н. Артеменко, А.Ф.
Волков, А.В. Зайцев, Письма в ЖЭТФ 37, 122 (1978).
-
[16] В.К. Каплуненко,
В.В. Рязанов, В.В. Шмидт ЖЭТФ 89, 1389 (1985).
-
[17] В.К. Каплуненко ФНТ12,
382 (1986).
-
[18] M.G. Blamier, E.C.G. Kirk, J.E. Evetts,
and T.M. Klapwijk, Phys. Rev. Lett.
66, 220 (1991).
-
[19] И.П. Невирковец, М.Г. Бламайер, Дж.Е.
Иветс, ФНТ
21, 1258 (1995).
-
[20] I.P. Nevirkovets, Phys. Rev. B 56,
832 (1997).
-
[21] Ф.В. Комиссинский, Г.А. Овсянников, Письма
в ЖЭТФ 61, 587 (1995).
-
[22] R. Kleiner, F. Steinmeyer, G. Kinkel, and
P. Muller, Phys. Rev. Lett. 68, 2394 (1992); R. Kleiner and P. Muller,
Phus. Rev. B 49, 1327 (1994).
-
[23] Yu.I. Latyshev and A.F. Volkov, Physica
(Amsterdam) 182C, 47 (1991); Yu.I. Latyshev, J.E. Nevelskaya, and
P. Monceau, Phys. Rev. Lett. 77, 932 (1996).
-
[24] F.X. Regi, J. Schneck, J.F. Palmier, and
H. Savary, J. Appl. Phys. 76, 4426 (1994).
-
[25] J. Takeya and S. Akita, Physica (Amsterdam)
235-240C,
3287 (1995).
-
[26]
-
A. Yurgens, D. Winkler, Y.M. Zhang, N. Zavaritsky, and T. Claeson, Physica
(Amsterdam) 235-240C, 3269 (1995).
-
[27]
-
Ji Ung Lee, J.E. Nordman, and G. Hohenwarter, Appl. Phys. Lett. 67,
1471 (1995).
-
[28]
-
M. Veith et al., J. Appl. Phys. 80, 3396 (1996).
-
[29]
-
K. Schlenga et al., Phys. Rev. Lett. 76, 4943 (1996).
-
[30]
-
A. Yurgens, D. Winkler, N.V. Zavaritsky, and T. Claeson, Phys. Rev. B 53,
R8887 (1996); Phys. Rev. Lett. 79, 5122 (1997).
-
[31]
-
K. Tanabe, Y. Hidaka, S. Karimoto, and M. Suzuki, Phys. Rev. B 53,
9348 (1996).
-
[32]
-
M. Rapp, A. Murk, R. Semerad, and W. Prusseit, Phys., Rev. Lett. 77,
928 (1996).
-
[33]
-
A. Odagawa, M. Sakai, H. Adachi, K. Setsune, T. Hirao, and K. Yoshida,
Jpn. J. Appl. Phys. 36, L21 (1997).
-
[34]
-
M. Itoh, S. Karimoto, K. Namekawa, and M. Suzuki, Phys. Rev. B 55,
R12001 (1997).
-
[35]
-
S.I. Yan, L. Fang, M.S. Si, and J. Wang, J. Appl. Phys.
82, 480
(1997)
-
[36]
-
H.L. Jonson, G. Hechtfischer, G. G?tz, R. Kleiner, and P. Muller, J. Appl.
Phys. 82, 756 (1997)
-
[37]
-
K. Schlenga et al., Phys. Rev. B 57, 14518 (1998)
-
[38]
-
T. Koyama and M. Tachiki, Phys. Rev. B 54, 16183 (1996).
-
[39]
-
S.N. Artemenko and A.G. Kobelkov, Phys. Rev. Lett.
78, 3551 (1997).
-
[40]
-
D.A. Ryndyk, cond-mat/9511001 (1995).
-
[41]
-
D.A. Ryndyk, Письма в ЖЭТФ 65, 755 (1997) [JETP Lett. 65,
791 (1997)].
-
[42]
-
D.A. Ryndyk, Phys. Rev. Lett. 80, 3376 (1998).
-
[43]
-
Д.А. Рындык, ЖЭТФ 116, 1798 (1999)
-
[44]
-
Г.М. Элиашберг, ЖЭТФ 61, 1254 (1971).
-
[45]
-
M. Tinkham and J. Clarke, Phys. Rev. Lett. 28, 1366 (1972); M. Tinkham,
Phys. Rev. B 6, 1747 (1972).
-
[46]
-
А.Г. Аронов, В.Л. Гуревич, ФТТ 16, 2656 (1974); A.G. Aronov, Yu.M.
Gal'perin, V.L. Gurevich, and V.I. Kozub, Adv. Phys.
30, 539 (1981).
-
[47]
-
А.Ф. Волков, А.В. Зайцев, ЖЭТФ 69, 2222 (1975).
-
[48]
-
L.N. Bulaevsky et al., Phys. Rev. B 50, 12 831 (1994).
-
[49]
-
L.N. Bulaevskii et al., Phys. Rev. B 53, 14 601 (1996); L.N. Bulaevskii
et al., Phys. Rev. B 54, 7521 (1996).
-
[50]
-
A.S. Mel'nikov, Phys. Rev. Lett. 77, 2786 (1996).
Автор: Рындык Дмитрий Александрович, e-mail: ryn@ipm.sci-nnov.ru


