В работе анализируются поляризационные характеристики рассеяния микроволнового излучения кристаллическими облачными частицами с различными распределениями по размерам, форме и ориентациям в пространстве. Обсуждаются возможности определения преимущественной ориентации частиц в облаке по характеристикам рассеянного излучения.

В последние годы большой интерес вызывает применение миллиметрового диапазона волн в атмосферных исследованиях. Примеры эффективного использования микроволнового излучения для зондирования облачности приведены в большом числе работ (см. обзор [1]).

Чувствительность многих современных метеорадаров такова, что они способны фиксировать деполяризующие свойства облачности. Характерная величина кроссполяризации (по мощности) обычно составляет ~ 10 ¸ 20 дБ [1], что для многих классов облаков является вполне обнаружимой величиной. Интенсивно обсуждаемое в последние годы повышение мощности микроволновых радаров [2, 3] может существенно расширить возможности поляризационных измерений. Представляется весьма заманчивым использовать результаты измерения кросс-поляризации рассеянного излучения для определения ориентации кристаллов в облаке. Такие измерения, в частности, могут быть использованы в исследованиях атмосферного электричества. В основе этой идеи лежит тот факт, что несферические ледяные облачные кристаллы существенно меняют свою ориентацию в зависимости от комбинации действующих на них гравитационных, аэродинамических и электрических сил. Однако необходимым условием реализации подобных измерений является подробное рассмотрение влияния размеров и формы кристаллов и их ориентации в пространстве на величину рассеянного сигнала в различных поляризациях. Известные работы, содержащие описание рассеяния микроволнового излучения на кристаллах различной формы (см., например [4, 5]) рассматривают только распределение по ориентациям, считающееся характерным для невозмущенной облачности [6] (плоскости пластин и длинные оси столбиков расположены горизонтально). В [5], кроме того, рассматривалось изотропное в пространстве распределение кристаллов по ориентациям. Если мы ставим задачу исследования атмосферного электричества по результатам экспериментального определения ориентации частиц, этого явно не достаточно. Известно, электризация атмосферы стремится ориентировать частицы вертикально [7], поэтому нельзя обойтись без рассмотрения различных типов ориентаций частиц вблизи вертикали.

Проведенный в данной работе анализ деполяризующих свойств облачности демонстрирует, что из сопоставления данных измерений с результатами численного моделирования рассеяния излучения в исследуемом объекте могут быть получены важные результаты.

Радиолокационная отражаемость единицы объема облака Z (обычно выражаемая в мм⁶м^-3) - мы следуем терминологии, используемой в [1], связана с радиолокационным сечением рассеяния единицы объема облака (измеряется в 1/м) следующим соотношением [8]: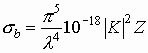

        (1)

где 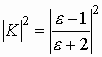, e - диэлектрическая проницаемость вещества частицы, а l - длина волны (в м). В случае идентичных сферических частиц, меньших длины волны Z = N D⁶ , где D - диаметр сферы (в мм), а N - концентрация частиц (в м^-3). Если имеется распределение частиц по размерам n(D), отражаемость записывается следующим образом:

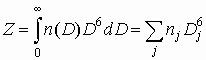     (2)

Для облака несферических частиц соотношение (1) определяет эквивалентную отражаемость Z_e [1].

Для несферических частиц отражаемость зависит не только от размера и концентрации частиц, но и от их формы, поляризации излучения и от ориентации частиц относительно направления зондирования. Известно [8], что ледяные кристаллы в облаках могут иметь сложную форму, но для оценок можно свести все многообразие к двум основным типам - столбчатые кристаллы (иглы и столбики) и пластинчатые [9]. В [4] было предпринято подробное исследование возможностей упрощения задачи рассеяния на таких частицах, что позволило сделать вывод о том, что на длине волны порядка 3 мм вполне оправданным является рассмотрение кристаллов в виде вытянутых и сплюснутых сфероидов с различными отношениями главных осей (до максимального размера кристаллов 1500 мкм). Более того, на этих волнах вплоть до максимального размера 800-1000 мкм с хорошей точностью можно рассматривать рассеяние как рэлеевское рассеяние на сфероидах, отношения главных осей которых соответствует тем же величинам в реальных кристаллах. Мы будем рассматривать следующие типы кристаллов и соответствующие им эмпирические выражения для соотношений размеров частиц в зависимости от типа [10]:

где L - больший размер кристалла (длина - для столбиков и игл, диаметр - для толстых и тонких пластин), h - меньший размер кристалла, все размеры даны в мкм.

А) Распределение, считающееся типичным для невозмущенного облака, - столбчатые кристаллы ориентированы длинной осью вдоль горизонта с равномерным распределением по азимутальному углу, плоскости пластинчатых кристаллов расположены горизонтально [6].

Б) Распределение, устанавливающееся при выстраивании частиц вдоль электрического поля в атмосфере [7] - длинные оси или плоскости ориентированы вертикально.

В) Распределение, которое можно считать переходным между А) и Б) - функция распределения ориентаций длинных осей кристаллов ~ cos²q , где q - угол отклонения большей оси сфероида от вертикали (в азимутальной плоскости распределение равномерное).

На Рис. 1 показаны зависимости этих величин от угла зондирования для отношения осей L/h=5 (угол зондирования отсчитывается от горизонта).

Видно, что величина рассеяния на кросс-поляризации примерно на два порядка меньше, чем на основной поляризации, что требует и соответствующего увеличения чувствительности приема. Кроме того, из рисунка видно, что вертикальное зондирование не дает возможности получить информацию из различия рассеяния в основных поляризациях, хотя информативность рассеяния в кросс-поляризации растет с увеличением угла наблюдения.

Деполяризационная диаграмма.

Сами по себе величины LDR и Z_vv/Z_hh определяются как структурой распределения частиц по ориентациям в пространстве, так и распределением частиц по эксцентриситетам, поэтому интерпретация подобных измерений, вообще говоря, весьма неоднозначна. Эффективным эвристическим методом анализа подобных измерений может являться построение диаграммы зависимости LDR от отношения Z_vv/Z_hh для различных эксцентриситетов (см. рис. 2). Положение экспериментальных точек относительно "разделительных линий" диаграммы может служить достаточно надежным указанием на преимущественную ориентацию частиц.

 Особенно важно отметить, что структура такой диаграммы (будем называть ее деполяризационной) практически не зависит от распределения частиц по размерам. распределение частиц по размерам в реальном облаке в литературе часто описывается модифицированным Г-распределением первого порядка [4]:

где D – диаметр эквивалентной сферы, D_m - т.н. "медианный диаметр объемного распределения", a - параметр, описывающий ширину распределения. Результаты оценок отношений Z_vv/Z_hh и LDR, сделанных для облака, в котором существует распределение кристаллов по размерам при различных значениях параметра D_m (в интервале 40-100 мкм [11]), приведены на рис. 3 кружками. Там же пунктиром показаны те же зависимости, что и на рис. 2. Видно, что учет распределения частиц по размерам не влияет на отношения величин рассеянных сигналов на различных поляризациях, т.е. оценки, сделанные без учета распределения по размерам, позволяют интерпретировать и результаты измерения рассеяния в реальном облаке. Заметим, что последний результат весьма нетривиален, т.к. использованная выше зависимость h(L) задает различные распределения по эксцентриситетам для различных распределений по диаметрам эквивалентных сфер. Хотя эффективность деполяризации весьма сильно зависит от эксцентриситетов частиц, структура деполяризационной диаграммы, как оказалось, определяется, в основном, ориентацией частиц. Такая универсальность деполяризационной диаграммы не случайна. Рассмотрим, например, набор из N различных эллипсоидов, ориентированных в одинаковом направлении. Ясно, что в приближении некогерентного рассеяния эта система будет рассеивать плоскую волну, как N аналогично ориентированных идентичных эллипсоидов при выполнении условия:

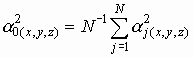
где a _j(x,y,z) – компоненты тензора поляризуемости j-той частиц в системе координат, связанной с частицей; a _0(x,y,z) – компоненты тензора поляризуемости частиц монодисперсного аэрозоля. Отсюда следует, что если распределения по ориентациям и эксцентриситетам независимы, то поляризационная диаграмма облака одинаковых частиц и облака частиц, имеющих распределение по размерам общего вида, идентичны.

Работа выполнена при поддержке РФФИ (грант N 98-02-17198).

1. Mead J.B., Pazmany A.L., Sekelsky S.M., McIntosh R.E. Millimeter-wave radars for remotely sensing clouds and precipitation // Proc. of IEEE. 1994. V. 82, N 12. P. 1981-1905.
   
2. Manheimer W.M. Gyrotron and free elecnron lasers as atmospheric sensor// Phys. Plasmas. 1994. v. 1, N 5. p. 1721-1729.
   
3. Manheimer W.M., Mesyats G.A., Petelin M.I. Super-high power microwave radars// Proc. 2nd Int. Conf. “Strong Microwaves in Plasmas”. IAP. N.Novgorod. 1993. v.2, p. 632-641.
   
4. Schneider T.L., Stephens G.L. Theoretical Aspects of Modeling Backscattering by Cirrus Ice Particles at Millimeter Wavelengths.// Journal of the Atmospheric Sciences. 1995. v. 52. N 23. p. 4367-4385.
   
5. C.Tang, K.Aydin. Scattering from Ice Crystals at 94 and 220 GHz Millimeter Wave Frequences.// IEEE Trans. Geosci. and Remote Sensing. 1995. v. 33, N 1, p. 93-99.
   
6. Cho H-R., Iribarne J.V., Richards W.G.. On the Orientation of Ice Crystals.// Journal of the Atmospheric Sciences. 1981. v. 38. N 5. p. 1111-1114
   
7. McEwan N.J., Alves A.P., Dissanayake A.W. OTS propagation measurements during thunderstorms.// Ann. Telecommunic.. 1981. V. 36, N 1-2 , P. 102-110.
   
8. Мазин И.П., Шметер С.М. Облака. Строение и физика образования. Л.: Гидрометеоиздат. 1983. 279 с.
   
9. Огути Т. Распространение и рассеяние электромагнитных волн в дожде и других гидрометеорах.// ТИИЭР. 1983. т. 71, N 9. с. 6-65.
   
10. Auer A.H., Veal D.L. The Dimension of Ice Crystals in Natural Clouds.// Journal of the Atmospheric Sciences. 1970. V. 27. P. 919-926.
    
11. Matrosov S.Y., Heymsfield A.J., Interieri J.M., Orr B.W., Snider J.B. Ground-based Remote Sensing of Cloud Particle Sizes during the 26 November 1991 FIRE II Cirrus Case: Comparisons with In Situ Data.// Journal of the Atmospheric Sciences. 1981. v. 52. N 23. p. 4128-4142.

Авторы: Моченева Ольга Станиславовна, тел. (8312)384566, e-mail: molga@appl.sci-nnov.ru,
               Токман Михаил Давидович, тел. (8312)360379, e-mail: tokman@appl.sci-nnov.ru
               Институт прикладной физики РАН
               603600, Нижний Новгород, ГСП-120, ул. Ульянова, д. 46, ИПФ РАН.

оглавление

дискуссия