|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 2003 |
|
СОКРАЩЕНИЕ ИЗБЫТОЧНОСТИ РАДИОЛОКАЦИОННОГО ИЗОБРАЖЕНИЯ НА ОСНОВЕ КАЛМАНОВСКОЙ ФИЛЬТРАЦИИ.
Галиев С.Ф., Лежанкин Б.В.
E-mail: gsf76@mail.ru
Иркутский ВАИИ.
Получена 23 января 2003 г.
Выполнен синтез квазиоптимального алгоритма сокращения избыточности радиолокационного изображения. Приведены результаты статистического моделирования синтезированного алгоритма на ЭВМ.
При дистанционном зондировании (ДЗ) земной поверхности с использованием радиолокационной станции с синтезированной апертурой (РСА) возникает проблема передачи в реальном масштабе времени (РМВ) потока данных (в частности изображений) на наземный пункт дешифрирования по причине низкой пропускной способности радиоканала (РК). Широкая полоса обзора поверхности земли и высокая разрешающая способность современных РСА не позволяют решить возникшую проблему без предварительной обработки радиолокационного изображения (РЛИ) на борту летательного аппарата с целью сокращения его избыточности (сжатия данных).
Существует
множество методов сокращения избыточности РЛИ, в том числе метод классификации
подстилающей поверхности, представленной на изображении в [1]. При этом учтено,
что поверхность, облучаемая РСА, большей частью представляет собой набор
однородных участков (ОУ) (лес, поле, пашня и др.), каждый из которых
характеризуется своей средней удельной эффективной поверхностью рассеяния (СУЭПР)
(![]() ). Использование
указанного метода предполагает постановку в соответствие каждому элементу
изображения (ЭИ) номера j СУЭПР
(класса подстилающей поверхности). Снижение требований к скорости передачи
данных достигается за счет передачи по РК информации не в виде значения яркости
каждого ЭИ, а в виде номера класса j и размеров
каждого ОУ.
). Использование
указанного метода предполагает постановку в соответствие каждому элементу
изображения (ЭИ) номера j СУЭПР
(класса подстилающей поверхности). Снижение требований к скорости передачи
данных достигается за счет передачи по РК информации не в виде значения яркости
каждого ЭИ, а в виде номера класса j и размеров
каждого ОУ.
Синтез алгоритма сокращения избыточности РЛИ методом классификации выполнен в [2] с использованием обобщенного гомоморфного преобразования и применением на этой основе калмановской фильтрации. Недостатком этого алгоритма является высокая ошибка в определении границы между ОУ при малом числе некогерентных накоплений и малом числе отношений их CУЭПР. Задачу повышения точности определения границы соседних ОУ возможно решить за счет учета в данном алгоритме статистических свойств облучаемой РСА подстилающей поверхности по двум координатам.
Цель работы – синтез алгоритма сокращения избыточности изображения РСА на основе калмановской фильтрации с учетом статистических свойств подстилающей поверхности по двум координатам и анализ его эффективности.
Синтез. Изображение подстилающей поверхности, облучаемой РСА, представим набором гауссовских полей с произвольными границами, соответствующими ОУ. При этом каждая строка формируемого РЛИ имеет вид дискретной последовательности значений яркости ЭИ, формируемой системой со случайной структурой [3]. Процесс формирования значения яркости ЭИ описывается уравнением наблюдения:
где ![]() — вектор наблюдения;
— вектор наблюдения; ![]() — вектор,
устанавливающий взаимосвязь между вектором сообщения
— вектор,
устанавливающий взаимосвязь между вектором сообщения ![]() и вектором наблюдений;
и вектором наблюдений; ![]() — значение гауссовского
шума наблюдения, описывающий изменение УЭПР относительно ее среднего значения; j — номер СУЭПР облучаемой поверхности
— значение гауссовского
шума наблюдения, описывающий изменение УЭПР относительно ее среднего значения; j — номер СУЭПР облучаемой поверхности ![]() .
.
Процесс формирования спекл-структуры описывается уравнением сообщения:
где ![]() — вектор сообщения
(фазовых координат), описывающий статистическую динамику двумерного поля на
дискретном множестве точек
— вектор сообщения
(фазовых координат), описывающий статистическую динамику двумерного поля на
дискретном множестве точек ![]() заданной области
заданной области ![]() , определяемых как
, определяемых как ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() — фундаментальная матрица, учитывающая
корреляционные связи между соседними элементами поля по строке
— фундаментальная матрица, учитывающая
корреляционные связи между соседними элементами поля по строке ![]() и по столбцу
и по столбцу ![]() ;
; ![]() — интервалы корреляции для подстилающей
поверхности по координатам
— интервалы корреляции для подстилающей
поверхности по координатам ![]() и
и ![]() ;
; ![]() — значение гауссовского формирующего шума
с нулевым математическим ожиданием;
— значение гауссовского формирующего шума
с нулевым математическим ожиданием; ![]() — вектор-столбец, состоящий из предыдущих
значений поля по строке —
— вектор-столбец, состоящий из предыдущих
значений поля по строке — ![]() , по столбцу —
, по столбцу — ![]() .
.
Двумерные гауссовские
случайные поля, описываемые в виде уравнений (1), (2), являются марковскими.
Свойство марковости дискретного случайного процесса состоит в том, что вероятность
значения этого процесса в момент времени ![]() зависит лишь от того, какое значение имел
процесс в предшествующий момент времени
зависит лишь от того, какое значение имел
процесс в предшествующий момент времени ![]() , и не зависит от значений процесса в более
ранние моменты времени. При этом моделируемые поля можно представить как
одномерные векторные марковские процессы, развертываемые по одной координате с
сохранением динамических свойств поля при дискретизации по другой координате
[4]. Следовательно, процессы смены номеров СУЭПР по координате
, и не зависит от значений процесса в более
ранние моменты времени. При этом моделируемые поля можно представить как
одномерные векторные марковские процессы, развертываемые по одной координате с
сохранением динамических свойств поля при дискретизации по другой координате
[4]. Следовательно, процессы смены номеров СУЭПР по координате ![]() (по строке) и
координате
(по строке) и
координате ![]() (по
столбцу) описываются дискретными марковскими последовательностями
(по
столбцу) описываются дискретными марковскими последовательностями ![]() и
и ![]() соответственно, состояния которых
являются значениями
соответственно, состояния которых
являются значениями ![]() в
соотношениях (1), (2). При этом случайные величины
в
соотношениях (1), (2). При этом случайные величины ![]() и
и ![]() образуют смешанную марковскую
последовательность с заданным вероятностным описанием в виде начальных
вероятностей
образуют смешанную марковскую
последовательность с заданным вероятностным описанием в виде начальных
вероятностей ![]() ,
,
![]() ,
, ![]() , матриц условных вероятностей
перехода
, матриц условных вероятностей
перехода ![]() ,
, ![]() , а также в виде
условных начальных и условных переходных плотностей вероятностей
, а также в виде
условных начальных и условных переходных плотностей вероятностей ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Каждое состояние ![]() условных марковских цепей
условных марковских цепей ![]() ,
, ![]() связано с некоторыми характеристиками,
определяющими структуру динамической системы (1), (2). Номер СУЭПР в каждый
момент времени
связано с некоторыми характеристиками,
определяющими структуру динамической системы (1), (2). Номер СУЭПР в каждый
момент времени ![]() случаен
и изменяется в соответствии с вероятностным механизмом, определяемым
последовательностями
случаен
и изменяется в соответствии с вероятностным механизмом, определяемым
последовательностями ![]() ,
,
![]() , а от
значений
, а от
значений ![]() ,
, ![]() не зависит. Поэтому выражения
(1) и (2) описывают РСА (в качестве формирователя РЛИ) как динамическую систему
со случайной структурой с независимыми распределенными параметрами [5],
генерирующую дискретное поле значений яркости ЭИ, а переходные вероятности принимают
вид:
не зависит. Поэтому выражения
(1) и (2) описывают РСА (в качестве формирователя РЛИ) как динамическую систему
со случайной структурой с независимыми распределенными параметрами [5],
генерирующую дискретное поле значений яркости ЭИ, а переходные вероятности принимают
вид: ![]() ,
, ![]() .
.
Алгоритм сокращения избыточности изображения РСА на основе калмановской
фильтрации состоит в оптимальной по критерию максимума апостериорной вероятности
оценки ![]() номера
СУЭПР и нахождении оптимальной по критерию минимума среднеквадратической ошибки
оценки
номера
СУЭПР и нахождении оптимальной по критерию минимума среднеквадратической ошибки
оценки ![]() вектора
фазовых координат
вектора
фазовых координат ![]() по
наблюдениям:
по
наблюдениям:
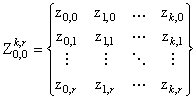 .
.
Основой для решения задачи фильтрации являются рекуррентные уравнения для
апостериорной плотности вероятности, описанные в [6]. В этом случае оптимальная
оценка номера СУЭПР ![]() определяется
выражением:
определяется
выражением:
а оценка ![]() и ковариационная
матрица ошибок оценивания
и ковариационная
матрица ошибок оценивания ![]() вектора фазовых координат
вектора фазовых координат ![]() определяются как
определяются как
Практическая реализация такого алгоритма чрезвычайно сложна из-за
постоянно возрастающего объема вычислений с ростом числа наблюдений ![]() . Поэтому возникает
необходимость перехода от оптимального алгоритма обработки к квазиоптимальному
за счет использования гауссовской аппроксимации апостериорной плотности
вероятности вектора фазовых координат. Используя обозначения для гауссовской
плотности вероятностей случайной величины
. Поэтому возникает
необходимость перехода от оптимального алгоритма обработки к квазиоптимальному
за счет использования гауссовской аппроксимации апостериорной плотности
вероятности вектора фазовых координат. Используя обозначения для гауссовской
плотности вероятностей случайной величины ![]() :
:
![]() ,
,
можно
представить плотности вероятностей случайных величин ![]() ,
, ![]() ,
, ![]() в виде:
в виде:
![]() ,
,
![]()
В рассматриваемом случае имеем ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где N — число некогерентных накоплений
РЛИ.
, где N — число некогерентных накоплений
РЛИ.
Используя гауссовскую аппроксимацию (6) получим выражение для вычисления апостериорной вероятности номеров СУЭПР:
![]()
где:
Апостериорное математическое ожидание ![]() и дисперсия ошибок оценивания
и дисперсия ошибок оценивания ![]() вычисляются как
вычисляются как
Для вычисления переменных, входящих в выражения (7-10), используем соотношения калмановского типа:
![]()
![]()
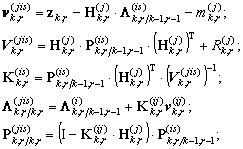
![]()
Начальные условия определяются следующим образом:
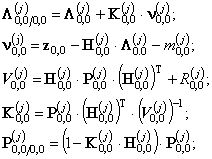
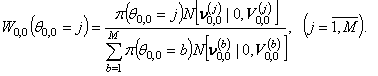
Для первой строки двумерного поля, за исключением начального значения,
когда ![]() ,
последующие значения вектора фазовых координат
,
последующие значения вектора фазовых координат ![]() и номера среднего СУЭПР
и номера среднего СУЭПР ![]() зависят только от
предыдущих значений по строке, поэтому переходные вероятности по столбцу
зависят только от
предыдущих значений по строке, поэтому переходные вероятности по столбцу ![]() и апостериорные
вероятности
и апостериорные
вероятности ![]() равны
нулю. При этом в алгоритме фильтрации не учитывается корреляционная связь с
предыдущими ЭИ по столбцу. В этом случае двумерный алгоритм превращается в
одномерный, рассмотренный в работе [2]. Аналогичные рассуждения можно
привести и для первого столбца, т.е. когда
равны
нулю. При этом в алгоритме фильтрации не учитывается корреляционная связь с
предыдущими ЭИ по столбцу. В этом случае двумерный алгоритм превращается в
одномерный, рассмотренный в работе [2]. Аналогичные рассуждения можно
привести и для первого столбца, т.е. когда ![]() , имеем
, имеем ![]() ,
, ![]() .
.
Таким
образом, в результате вычислений согласно приведенным рекуррентным уравнениям
алгоритма сокращения избыточности РЛИ для каждого ЭИ получаем оценку ![]() номера СУЭПР по максимальному значению апостериорной
вероятности
номера СУЭПР по максимальному значению апостериорной
вероятности ![]() ,
,![]() .
.
Моделирование. Аналитическое исследование характеристик разработанного квазиоптимального алгоритма сокращения избыточности РЛИ оказывается невозможным. Поэтому его исследование было проведено путем статистического моделирования на ЭВМ.
Эффективность алгоритма характеризуется точностью определения границы
классифицируемых ОУ, представляемой зависимостью ошибки определения состояния ![]() от номера шага
от номера шага ![]() ,
, ![]() (что представлено на всех
рисунках), начиная с момента перехода от участка местности с одним номером
среднего значения УЭПР к участку местности с другим номером среднего значения
УЭПР:
(что представлено на всех
рисунках), начиная с момента перехода от участка местности с одним номером
среднего значения УЭПР к участку местности с другим номером среднего значения
УЭПР:
где ![]() — число реализаций, по которым производится
усреднение;
— число реализаций, по которым производится
усреднение; ![]() —
величина, принимающая значение нуль в случае, когда номер СУЭПР
—
величина, принимающая значение нуль в случае, когда номер СУЭПР ![]() и его
оценка
и его
оценка ![]() на
шаге
на
шаге ![]() ,
, ![]() совпадают, и равная
единице в противном случае. Например, значение
совпадают, и равная
единице в противном случае. Например, значение ![]() означает, что в двух случаях из десяти
оценка номера СУЭПР данного ЭИ была произведена неправильно.
означает, что в двух случаях из десяти
оценка номера СУЭПР данного ЭИ была произведена неправильно.
При моделировании РЛИ на ЭВМ согласно выражений (1) и (2) формировалось
изображение в виде тестового «шахматного» поля 1000х1000 ЭИ, представленное
двумя классами поверхности ![]() . Рассматриваемый случай является
упрощением. Однако его анализ позволяет получить наглядные характеристики
работы алгоритма, которые будут иметь место и при большом числе классов подстилающей
поверхности.
. Рассматриваемый случай является
упрощением. Однако его анализ позволяет получить наглядные характеристики
работы алгоритма, которые будут иметь место и при большом числе классов подстилающей
поверхности.
Обработка изображения с помощью синтезированного алгоритма сокращения
избыточности производилась при соответствующих значениях N,
![]() ,
, ![]() и
и ![]() .
.
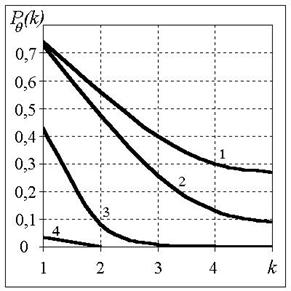
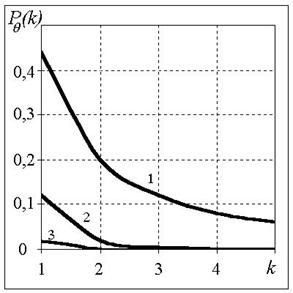
Рис. 1, 2 характеризуют эффективность работы алгоритма в зависимости от ![]() , на них представлены
графики зависимости
, на них представлены
графики зависимости ![]() для
различных отношений СУЭПР
для
различных отношений СУЭПР ![]() , равных двум и четырем соответственно.
Матрица переходных вероятностей
, равных двум и четырем соответственно.
Матрица переходных вероятностей ![]() выбиралась симметричной и равной
выбиралась симметричной и равной ![]() . Элементами матрицы
. Элементами матрицы ![]() являются переходные
вероятности от номера СУЭПР
являются переходные
вероятности от номера СУЭПР ![]() к номеру СУЭПР
к номеру СУЭПР ![]() , а элементами матрицы
, а элементами матрицы ![]() являются переходные
вероятности от номера СУЭПР
являются переходные
вероятности от номера СУЭПР ![]() к номеру СУЭПР
к номеру СУЭПР ![]() ,
, ![]() . Цифрами на рис. 1,
2 обозначены графики
для случаев: 1 - N=1; 2 - N=2;
3 - N=4; 4 - N=7.
. Цифрами на рис. 1,
2 обозначены графики
для случаев: 1 - N=1; 2 - N=2;
3 - N=4; 4 - N=7.
Рис. 1. Рис. 2.
Из
рис. 1,2
видно, что с увеличением числа некогерентных накоплений N
резко уменьшается ошибка в определении границы соседних ОУ; при отношении
средних значений УЭПР классифицируемых участков местности ![]() и N>4
точность определения границы смены соседних ОУ составляет 1…2 ЭИ.
и N>4
точность определения границы смены соседних ОУ составляет 1…2 ЭИ.
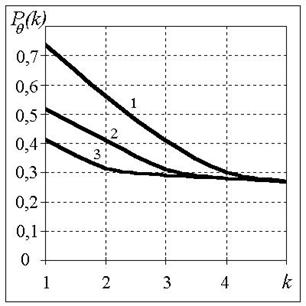
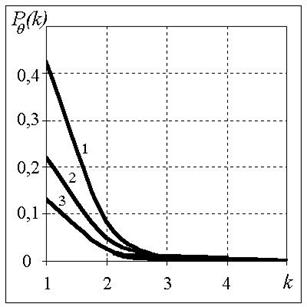
Рис. 3. Рис. 4.
Рис. 3, 4 характеризуют эффективность работы алгоритма в зависимости от
вида матриц переходных вероятностей ![]() ,
, ![]() , на них представлены графики зависимости
, на них представлены графики зависимости ![]() при
при ![]() , N=1 и N=4 соответственно. Цифрами обозначены графики для случаев 1
-
, N=1 и N=4 соответственно. Цифрами обозначены графики для случаев 1
- ![]() ; 2 -
; 2 - ![]() ; 3 -
; 3 - ![]() .
.
Из
рис. 3,4
видно, что с уменьшением отношения переходных вероятностей соседних элементов
матриц ошибка определения состояния ![]() при переходе границы ОУ быстро уменьшается,
однако эта зависимость имеет место только до значений
при переходе границы ОУ быстро уменьшается,
однако эта зависимость имеет место только до значений ![]() . В том случае, когда число
некогерентных накоплений N>4, ошибка в определении границы
ОУ не превышает 3 ЭИ.
. В том случае, когда число
некогерентных накоплений N>4, ошибка в определении границы
ОУ не превышает 3 ЭИ.
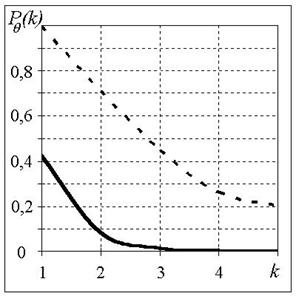
Рис. 5
позволяет сравнить эффективность двумерного (сплошная линия) и одномерного
(пунктирная линия) алгоритмов сокращения избыточности при следующих параметрах
изображения: N=4, ![]() ,
, ![]() .
.
Рис. 5.
Анализ графиков на рис. 5 показывает, что учет в алгоритме сокращения избыточности корреляционных свойств подстилающей поверхности по двум координатам позволяет повысить его эффективность более, чем в два раза.
Таким образом, полученные в ходе статистического моделирования характеристики синтезированного алгоритма показывают его достаточно высокую эффективность при решении задачи сокращения избыточности РЛИ.
Литература
1. Ulaby F.T., Li R.Y., Shunmugan K.S.Crop classification using airborne radar and Landsatdata // IEEE Trans.: V.GE-20.-1982.-No.1.-P.42-50.
2. Мансуров В.В., Миронов Б.М. Алгоритм сокращения избыточности радиолокационного изображения // Радиоэлектроника. — 1992, №4, с. 54 — 58. (Изв. высш. учебн. заведений).
3. Казаков И.Е., Артемьев В.М. Оптимизация динамических систем случайной структуры. – М.: Наука, 1980. – 384 с.
4. Розанов Ю.А. Теория вероятностей, случайные процессы и математическая статистика. Учебник для вузов. - 2-е изд., доп. - М.: Наука, 1987. – 320 с.
5. Васильев К.К., Крашенинников В.Р. Методы фильтрации многомерных случайных полей. – Саратов: Изд-во Сарат. Ун-та., 1990.
6. Клекис Э.А. Оптимальная фильтрация в системах со случайной структурой и дискретным временем // Автоматика и телемеханика. – 1987. - №11 - С. 61-70.
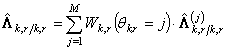 , (4)
, (4)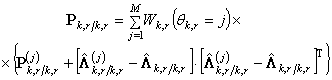 .
.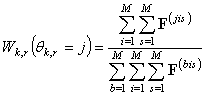 , (
, (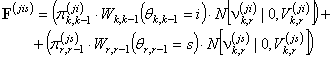 (8)
(8)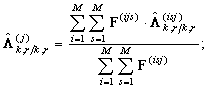
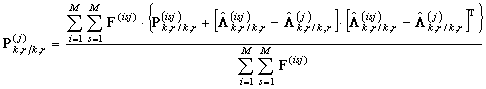 .(10)
.(10)