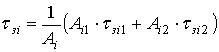УДК 621.396.96
Оценка искажений отклика приемника РЛС на сигнал, формируемый с помощью двухточечной модели
Р. Ю. Белоруцкий
Новосибирский государственный технический университет
Получена 16 января 2012 г.
Аннотация. Рассмотрено формирование эхосигнала от точечного отражателя с помощью двухточечной модели. Получены аналитические соотношения для оценки искажений отклика приемника РЛС на формируемый сигнал.
Ключевые слова: имитационное моделирование эхосигналов, двухточечная модель, радиолокация.
Abstract. Forming echo signal reflected from the point reflector using the two-point model is considered. The analytical expressions for estimating distortions of radar receiving set response to the formed signal are obtained.
Keywords: radar echo simulation modeling, two-point model, radiolocation.
Введение
Известным способом тестирования радиолокационных станций является проведение полунатурных экспериментов с использованием специальных технических средств – имитаторов эхосигналов [1]. При этом в испытательных лабораториях моделируется полет носителя РЛС, а на вход приемника станции подаются эхосигналы, сформированные имитатором.
Имитация эхосигналов радиолокационных станций с синтезированием апертуры антенны (РСА) предполагает моделирование сигнала, отражаемого от поверхности Земли. Для этого зондируемый участок поверхности представляется набором из эквивалентных точечных отражателей, разбивается на полоски равных дальностей, и для каждой полоски производится расчет суммарного эхосигнала от отражателей, попадающих в её пределы. Имитируемый эхосигнал является совокупностью сигналов от всех полосок.
При движении носителя РЛС происходит изменение ракурса наблюдения участка поверхности, которое влечет за собой изменение положения полосок равных дальностей. В результате происходит перераспределение эквивалентных отражателей между ними. Вследствие того, что значения задержек элементов дальности имитатора принимают дискретные значения, возникает частная проблема, состоящая в необходимости обеспечения плавного перехода имитируемого отражателя между двумя соседними полосками. При этом должно обеспечиваться требуемое положение отражателя по наклонной и путевой дальностям. В то же время, разделение сигнала на элементы дальности необходимо, т.к. диктуется экономией вычислительных ресурсов, используемых для его формирования в режиме реального времени [2]. Выходом из ситуации является применение двухточечной модели с зависимыми отражателями [3].
Рассмотрим задачу обеспечения необходимого положения отражателя, когда он заменяется эквивалентным центром излучения (ЭЦИ) системы из двух зависимых неразрешаемых отражателей. Положение по наклонной дальности определяется временем задержки эхосигнала. В данном случае отражателям двухточечной модели соответствуют сигналы с фиксированными задержками, относящиеся к соседним элементам дальности имитатора. Они имеют ту же форму, что и имитируемый сигнал, отличаясь амплитудами. Значения амплитуд связаны и определяются координатой ЭЦИ [3]:
где ![]() ,
, ![]() и
и ![]() ,
, ![]() – амплитуды и задержки сигналов от
отражателей двухточечной модели (
– амплитуды и задержки сигналов от
отражателей двухточечной модели (![]() );
); ![]() ,
, ![]() –
амплитуда и задержка (координата ЭЦИ) сигнала от имитируемого отражателя;
–
амплитуда и задержка (координата ЭЦИ) сигнала от имитируемого отражателя; ![]() .
.
При условии неизменности мощности сигнала должно выполняться условие:
![]() .
(2)
.
(2)
Согласно (1), (2) амплитуды сигналов от отражателей модели рассчитываются как:
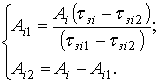 (3)
(3)
Положение точечного отражателя по путевой дальности в режиме синтезирования апертуры определяется законом изменения фазы эхосигнала. Необходимо, чтобы фаза сигнала от двухточечной модели соответствовала фазе имитируемого сигнала. Очевидно, что сигналы от соседних элементов дальности в точке приема будут иметь разные фазы, определяемые задержками:
![]() ,
, ![]() ,
,
где ![]() – частота зондирующего
сигнала;
– частота зондирующего
сигнала; ![]() и
и ![]() –
фазовые набеги пропорциональные задержкам
–
фазовые набеги пропорциональные задержкам ![]() и
и ![]() сигналов от отражателей двухточечной модели.
сигналов от отражателей двухточечной модели.
Для достижения требуемого
результирующего значения фазы сигнала от модели необходимо корректировать фазы сигналов
от обоих отражателей на значения ![]() и
и ![]() , чтобы в точке приема
, чтобы в точке приема
![]() ,
(4)
,
(4)
где ![]() – фаза сигнала от имитируемого
отражателя.
– фаза сигнала от имитируемого
отражателя.
Постановка задачи
Рассмотрим форму отклика приемника РЛС на сигнал, формируемый с помощью двухточечной модели. Отклик линейного тракта приемника является суммой откликов на сигналы от отражателей модели:
![]() .
(5)
.
(5)
В качестве эталонной формы отклика на сигнал, отраженный от одиночного отражателя, будем рассматривать треугольную, имеющую место при согласованной обработке простого импульсного зондирующего сигнала единичной амплитуды:
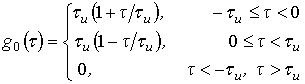 (6)
(6)
где
![]() – длительность импульса.
– длительность импульса.
Согласно условию неразрешимости отражателей:
![]() ,
(7)
,
(7)
где ![]() – размер модели.
– размер модели.
Согласно (5), (6), (7) отклик на сигнал от двухточечной модели:
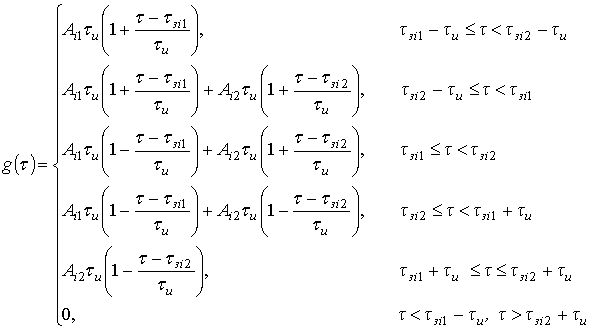 (8)
(8)
Таким образом, огибающая ![]() описывается кусочно-линейной функцией
(рис. 1) на пяти интервалах:
описывается кусочно-линейной функцией
(рис. 1) на пяти интервалах:
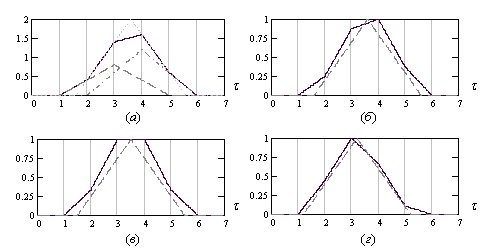
Рис. 1.
Искаженный, эталонный, а также отдельные отклики на сигналы от
отражателей модели при ![]() (а); нормированные искаженный и
эталонный отклики при
(а); нормированные искаженный и
эталонный отклики при ![]() (б), при
(б), при ![]() (в), при
(в), при ![]() (г)
(г)
(![]() ,
, ![]() ,
, ![]() ).
).
Видно, что форма ![]() отличается от эталонной треугольной. Степень
искажения отклика зависит от координаты ЭЦИ и отношения размера модели к
длительности импульса
отличается от эталонной треугольной. Степень
искажения отклика зависит от координаты ЭЦИ и отношения размера модели к
длительности импульса ![]() . Для адекватного моделирования
необходимо знать влияние этих параметров на форму отклика.
. Для адекватного моделирования
необходимо знать влияние этих параметров на форму отклика.
Цель работы
Оценить искажения отклика РЛС при формировании имитируемого эхосигнала с помощью двухточечной модели.
Решение
Оценим искажения отклика по следующим критериям: уменьшению максимального значения, смещению максимума, изменению ширины, смещению центра тяжести и середины сечения.
1.
Уменьшение максимального значения ![]() по сравнению с эталонным откликом
по сравнению с эталонным откликом ![]() можно оценить как отношение максимума
искаженного отклика к максимуму эталонного. Обозначим это отношение
коэффициентом:
можно оценить как отношение максимума
искаженного отклика к максимуму эталонного. Обозначим это отношение
коэффициентом:
 (10)
(10)
Например, для искаженного отклика,
изображенного на рис. 1а, ![]() . На рис. 2а приведены
примеры зависимостей коэффициента
. На рис. 2а приведены
примеры зависимостей коэффициента ![]() от положения ЭЦИ,
задаваемого соотношением (1). Зависимости получены для значений
от положения ЭЦИ,
задаваемого соотношением (1). Зависимости получены для значений ![]() .
.
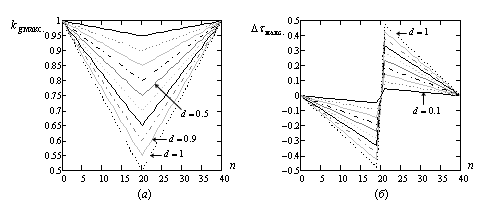
Рис. 2.
Графики зависимости коэффициента уменьшения максимального значения ![]() (а) и смещения максимума
(а) и смещения максимума ![]() (б) отклика от положения ЭЦИ
(б) отклика от положения ЭЦИ
(значение ![]() нормировано к длительности импульса
нормировано к длительности импульса ![]() ).
).
Здесь ![]() –
номер шага изменения временной координаты ЭЦИ (
–
номер шага изменения временной координаты ЭЦИ (![]() ) от
значения
) от
значения ![]() к
к ![]() . Шаг
составляет
. Шаг
составляет ![]() :
: ![]() .
.
2. Смещение максимума отклика относительно задаваемого ЭЦИ.
Максимальное значение ![]() всегда приходится на координату отражателя
с наибольшей амплитудой:
всегда приходится на координату отражателя
с наибольшей амплитудой: ![]() , если
, если ![]() и
и ![]() , если
, если
![]() . Поэтому смещение максимума
. Поэтому смещение максимума ![]() находится как разность координат ЭЦИ и
ближайшего к нему отражателя модели:
находится как разность координат ЭЦИ и
ближайшего к нему отражателя модели:
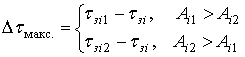
Например, для рис. 1а ![]() . В случае
. В случае ![]() ЭЦИ
находится в середине промежутка между отражателями, при этом форма отклика
имеет симметричный вид, а вершина – плоскую форму (рис. 1в). На рис. 2б изображена
зависимость
ЭЦИ
находится в середине промежутка между отражателями, при этом форма отклика
имеет симметричный вид, а вершина – плоскую форму (рис. 1в). На рис. 2б изображена
зависимость ![]() от положения ЭЦИ.
от положения ЭЦИ.
3. Изменение ширины отклика.
Получим выражение для определения
ширины сечения нормированного искаженного отклика по уровню ![]() . Очевидно, что она должна находиться как
. Очевидно, что она должна находиться как
где ![]() и
и ![]() – координаты границ сечения отклика
соответственно по левую и правую сторону относительно вершины.
– координаты границ сечения отклика
соответственно по левую и правую сторону относительно вершины.
Для нахождения ![]() и
и
![]() необходимо решить уравнение:
необходимо решить уравнение:
Так как огибающая отклика ![]() описывается разными выражениями на пяти
интервалах (9), перед решением (12) необходимо установить, в какие из них
попадают границы сечения отклика. Далее в соответствии с интервалами выбираем пару
выражений
описывается разными выражениями на пяти
интервалах (9), перед решением (12) необходимо установить, в какие из них
попадают границы сечения отклика. Далее в соответствии с интервалами выбираем пару
выражений ![]() и дважды решаем (12), находя
и дважды решаем (12), находя ![]() и
и ![]() . Для нахождения
ширины сечения по произвольному уровню
. Для нахождения
ширины сечения по произвольному уровню ![]() необходимо
определить все возможные комбинации пар уравнений (12). Несложно показать, что
существует 4 варианта формы искаженного отклика
необходимо
определить все возможные комбинации пар уравнений (12). Несложно показать, что
существует 4 варианта формы искаженного отклика ![]() : по
два для каждого положения вершины (рис. 3). Варианты отличаются друг от друга взаимным
положением точек излома огибающей.
: по
два для каждого положения вершины (рис. 3). Варианты отличаются друг от друга взаимным
положением точек излома огибающей.
В случае ![]() форма отклика, соответствующая варианту
№1 (рис. 3а), наблюдается, когда
форма отклика, соответствующая варианту
№1 (рис. 3а), наблюдается, когда
а варианту №2 (рис. 3б) – когда
![]() . (14)
. (14)
Для случая ![]() вариант №1 (рис. 3в) имеет место при условии
вариант №1 (рис. 3в) имеет место при условии
![]() , (15)
, (15)
а №2 (рис. 3г) – при условии
![]() . (16)
. (16)

Рис. 3.
Варианты формы отклика при ![]() : №1 – (а), №2 – (б);
: №1 – (а), №2 – (б);
при ![]() : №1 – (в), №2 – (г).
: №1 – (в), №2 – (г).
В свою очередь, огибающую
отклика в случае каждого из четырех вариантов можно разделить на четыре участка
по уровню ![]() (рис. 3: нумерация установлена
снизу вверх). При этом каждому из них будет соответствовать своя пара уравнений
(12).
(рис. 3: нумерация установлена
снизу вверх). При этом каждому из них будет соответствовать своя пара уравнений
(12).
Для того чтобы определить,
какому участку принадлежит уровень сечения ![]() ,
необходимо проверить последовательно следующие неравенства.
,
необходимо проверить последовательно следующие неравенства.
I. При ![]()
Участок 1:
![]() . (17)
. (17)
Если при обозначении участка используется две цифры, то первая указывает его номер, вторая – номер варианта формы отклика.
Участок 2.1 (при выполнении условия (13)):
![]() . (18)
. (18)
Участок 2.2 (при выполнении условия (14)):
![]() . (19)
. (19)
Участок 3.1 (при выполнении (13)):
![]() . (20)
. (20)
Участок 3.2 (при выполнении (14)):
![]() . (21)
. (21)
Участок 4.1 (при выполнении (13)):
![]() . (22)
. (22)
Участок 4.2 (при выполнении (14)):
![]() .
(23)
.
(23)
II. При ![]()
Участок 1:
![]() .
(24)
.
(24)
Участок 2.1 (при выполнении (15)):
![]() . (25)
. (25)
Участок 2.2 (при выполнении (16)):
![]() . (26)
. (26)
Участок 3.1 (при выполнении (15)):
![]() . (27)
. (27)
Участок 3.2 (при выполнении (16)):
![]() . (28)
. (28)
Участок 4.1 (при выполнении (15)):
![]() . (29)
. (29)
Участок 4.2 (при выполнении (16)):
После решения уравнений (12), соответствующих условиям (17)-(30), исходя из (11) получена система выражений для определения ширины сечения нормированного искаженного отклика:
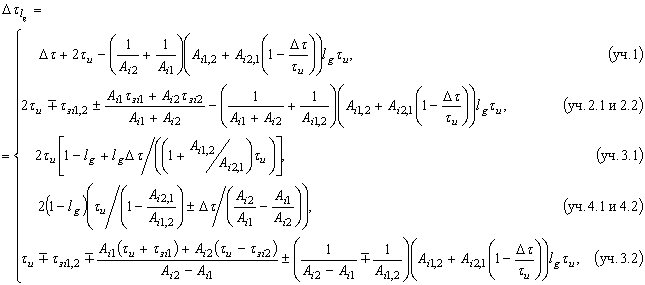 (31)
(31)
где при обозначении ![]() ,
, ![]() ,
, ![]() ,
, ![]() и «
и «![]() », «
», «![]() » первая цифра индекса и верхний знак относятся
к случаю
» первая цифра индекса и верхний знак относятся
к случаю ![]() , вторая цифра и нижний знак – к
, вторая цифра и нижний знак – к ![]() . Перед использованием (31), опираясь на условия
(13)-(30), необходимо определить, какому участку принадлежит
. Перед использованием (31), опираясь на условия
(13)-(30), необходимо определить, какому участку принадлежит ![]() , и выбрать соответствующее выражение для
расчета
, и выбрать соответствующее выражение для
расчета ![]() .
.
Ширина сечения нормированного эталонного (треугольного) отклика определяется как
![]() .
(32)
.
(32)
Рассмотрим графики, построенные на основе (31).
На рис. 4 приведены примеры зависимостей нормированной ширины сечения
искаженного отклика от положения ЭЦИ, задаваемого соотношением (1). Зависимости
получены для ![]() . Нормирование произведено к
значению ширины эталонного отклика (32). Семейство зависимостей для сечения по
уровню
. Нормирование произведено к
значению ширины эталонного отклика (32). Семейство зависимостей для сечения по
уровню ![]() представлено на рис. 4а, для
представлено на рис. 4а, для ![]() – на рис. 4б, для
– на рис. 4б, для ![]() –
на рис. 4г.
–
на рис. 4г.
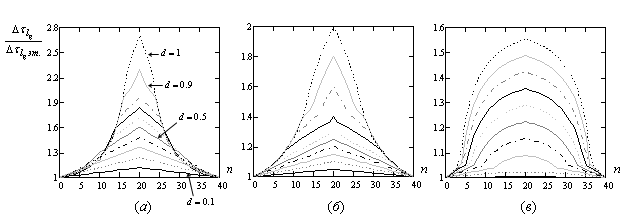
Рис. 4. Графики зависимостей нормированной ширины
искаженного
отклика от положения ЭЦИ.
При ![]() координата
ЭЦИ совпадает со значением задержки сигнала от первого отражателя (
координата
ЭЦИ совпадает со значением задержки сигнала от первого отражателя (![]() ), а при
), а при ![]() – от
второго (
– от
второго (![]() ). В этих случаях сигнал от двухточечной
модели идентичен имитируемому сигналу, а форма отклика – эталонной,
соответственно
). В этих случаях сигнал от двухточечной
модели идентичен имитируемому сигналу, а форма отклика – эталонной,
соответственно ![]() . Когда
. Когда ![]() ,
ЭЦИ находится в середине промежутка между отражателями, при этом наблюдается
наибольшее расширение отклика относительно эталонного. Видно, что расширение
растет вместе со значением
,
ЭЦИ находится в середине промежутка между отражателями, при этом наблюдается
наибольшее расширение отклика относительно эталонного. Видно, что расширение
растет вместе со значением ![]() и по мере приближения
ЭЦИ к середине интервала между отражателями модели.
и по мере приближения
ЭЦИ к середине интервала между отражателями модели.
4. Смещение центра тяжести отклика.
Известно, что в РЛС с автоматическим измерением дальности задержка эхосигнала может определяться по положению центра тяжести (ЦТ) отклика [4]. Используем этот параметр в качестве критерия оценки искажений отклика.
Координата ЦТ ![]() отклика определяется через решение
интегрального уравнения:
отклика определяется через решение
интегрального уравнения:
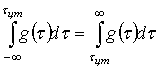 .
(33)
.
(33)
Для решения (33) представим интегралы в виде
сумм отдельных интегралов на интервалах (9). Так как отдельные отклики на
сигналы от отражателей модели являются симметричными фигурами, координата
центра тяжести ![]() будет находиться в интервале
будет находиться в интервале ![]() , разбивая его на отрезки
, разбивая его на отрезки ![]() и
и ![]() .
Интегралы, вычисленные на этих отрезках, будут относиться к левой и правой
частям уравнения (33) соответственно:
.
Интегралы, вычисленные на этих отрезках, будут относиться к левой и правой
частям уравнения (33) соответственно:
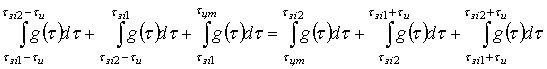 . (34)
. (34)
После преобразований (34) сводится к:
![]() ,
(35)
,
(35)
где
![]() ;
;
![]() ;
;![]() .
.
Из двух корней (35) выбирается тот, который удовлетворяет
условию ![]() . В случае, если
. В случае, если ![]() ,
центр тяжести совпадает с ЭЦИ, тогда
,
центр тяжести совпадает с ЭЦИ, тогда ![]() .
.
Зная координату ЦТ, несложно определить её отклонение относительно ЭЦИ:
![]() .
.
На рис. 5в приведены графики
зависимости ![]() от координаты ЭЦИ для разных значений
от координаты ЭЦИ для разных значений ![]() . Видно, что величина
. Видно, что величина ![]() растет вместе с
растет вместе с ![]() .
.
5. Отклонение середины сечения отклика от задаваемого ЭЦИ.
Известно, что при визуальной оценке человек-оператор определяет положение отметки на РЛИ по положению её середины [5]. Используем в качестве ещё одного критерия оценки искажений положение середины сечения отклика.
Середина сечения эталонного
отклика совпадает с координатами вершины и центра тяжести ввиду симметрии его
фигуры. Очевидно, что искаженный отклик не обладает таким свойством. Положение
середины сечения по уровню ![]() можно найти как
можно найти как
![]() .
(36)
.
(36)
На основе подхода, описанного в п. 3, исходя из (36) получена система выражений для определения координаты середины сечения нормированного искаженного отклика:
 (37)
(37)
где при обозначении ![]() ,
, ![]() ,
, ![]() ,
, ![]() и «
и «![]() », «
», «![]() » первая цифра индекса и верхний знак относятся
к случаю
» первая цифра индекса и верхний знак относятся
к случаю ![]() , вторая цифра и нижний знак – к
, вторая цифра и нижний знак – к ![]() . Перед использованием (37), опираясь на (13)-(30),
необходимо определить, какому участку принадлежит
. Перед использованием (37), опираясь на (13)-(30),
необходимо определить, какому участку принадлежит ![]() и
выбрать соответствующее выражение для расчета
и
выбрать соответствующее выражение для расчета ![]() .
.
Отклонение середины сечения отклика от координаты ЭЦИ найдем как:
![]() .
.
На рис. 5 изображены примеры
графиков ![]() как функции от координаты ЭЦИ: для
сечения по уровню
как функции от координаты ЭЦИ: для
сечения по уровню ![]() (а) и
(а) и ![]() (б).
(б).
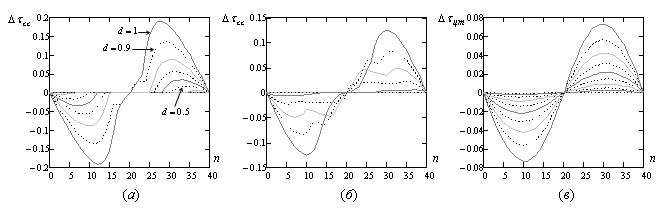
Рис. 5.
Графики отклонения середины сечения (а), (б) и
центра тяжести отклика от ЭЦИ (в) как функций от координаты ЭЦИ
(величина отклонений нормирована к длительности импульса ![]() ).
).
Видно, что величина отклонений
также увеличивается вместе с ![]() . Координата середины
сечения совпадает с ЭЦИ (
. Координата середины
сечения совпадает с ЭЦИ (![]() ) в случае симметрии отклика
(при
) в случае симметрии отклика
(при ![]() ).
).
Выводы
Применение двухточечной модели приводит к искажениям отклика приемника РЛС, заключающимся в уменьшении максимального значения, изменении ширины, смещении центра тяжести и середины сечения отклика относительно задаваемого положения ЭЦИ.
Получены аналитические соотношения для оценки искажений отклика по данным критериям.
Настоящие соотношения позволят
определить допустимое значение отношения ![]() , при
котором искажения отклика РЛС не будут выходить за заданные пределы. Этим будет
обеспечиваться адекватность моделирования эхо-сигнала при имитации.
, при
котором искажения отклика РЛС не будут выходить за заданные пределы. Этим будет
обеспечиваться адекватность моделирования эхо-сигнала при имитации.
Рассмотренный подход позволит формировать эхосигналы РСА при строчной структуре формируемого РЛИ и смене ракурса наблюдения зондируемого участка в процессе имитации.
Литература
1. В.Н. Антипов, В.Т. Горяинов, А.Н. Кулин и др. Радиолокационные станции с цифровым синтезированием апертуры антенны/ Под ред. В.Т. Горяинова. – М.: Радио и связь, 1988 – 304 с.
2. Белоруцкий Р.Ю., Киселев А.В., Тырыкин С.В. Два алгоритма формирования эхо-сигналов от сложного радиолокационного объекта/ Материалы X международной конференции «Актуальные проблемы электронного приборостроения», Новосибирск , 22-24 сентября, 2010 г. – Новосибирск , НГТУ, 2010 г., том 4, с. 29-32
3. Тырыкин С.В., Киселёв А.В. Ошибка оценки задержки эхосигнала от сложного радиолокационного объекта, моделируемого набором дискретных отражателей // Сборник научных трудов НГТУ, Новосибирск, НГТУ, 2001. – №4(26)., С. 63–68.
4.
Жуковский
А.П., Оноприенко Е.И., Чижов В.И. Теоретические основы
радиовысотометрии. Под ред. А. П. Жуковского. – М.: Сов. радио, 1979. – 320 с.
5. Слуцкий В.З., Фогельсон Б.И. Импульсная техника и основы радиолокации. Изд. 3-е, переработ. и дополн. – М.: Воениздат, 1975. – 439 с.