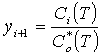УДК: 616.8/831.2-072

Задача распознавания образов для диагностики болезни Паркинсона по данным ЭЭГ

Ф. Н. Григорьев, Н. А. Кузнецов

Институт радиотехники и электроники им. В.А. Котельникова РАН

Получена 26 января 2012 г.

Аннотация. Для диагностики болезни Паркинсона определяется вектор оценок нормированной корреляционной последовательности сигнала О2-А2 ЭЭГ пациента. Построено линейное решающее правило – гиперплоскость, разделяющая множество векторов, соответствующих больным и здоровым пациентам. Проведено моделирование диагностики заболеваний по реальным данным.

Ключевые слова: диагностика, болезнь Паркинсона, оценка, нормированная корреляционная последовательность, линейное решающее правило, разделяющая гиперплоскость.

Abstarct. The vector of estimates of normalized correlation sequence for signal O2-A2 EEG patient was defined for the diagnosis of Parkinson's disease. The linear decision rule - a hyperplane separating the sets of vectors corresponding to the patients and healthy individuals was created. The simulation of disease diagnosis in the real data was made.

Keywords: diagnosis, Parkinson’s disease, estimate, normalized correlation sequence, linear decision rule, decomposable hyperplane.

Введение

В настоящее время запись электроэнцефалограмм (ЭЭГ) стала общедоступной процедурой. Она достаточно проста и занимает немного времени. Однако расшифровка полученной записи трудоемка и неоднозначна, требует высокой квалификации от специалиста, а время на расшифровку ЭЭГ при массовых процедурах весьма ограничено. Поэтому необходимо иметь возможность объективно оценивать здоровье пациентов с помощью простого в обслуживании современного аппаратурного анализа ЭЭГ, автоматически дающего заключение, оформленное в доступной для практикующих врачей форме.

Для расшифровки записей энцефалограмм в качестве исследовательского инструмента многократно использовались различные математические методы корреляционного анализа, спектрально-когерентного анализа, топографического картирования данных, вейвлет-анализа и пр. Они были успешно апробированы для диагностики неврологических заболеваний, в частности болезни Паркинсона.

Существенные успехи в появившейся возможности записывать сигналы энцефалограмм выдвигают новую проблему – необходимость разработки автоматических алгоритмов анализа этих сигналов, как по определению нормы и диагностики патологических состояний, так и анализа откликов на тестовые воздействия на пациента. Решать подобные задачи возможно на основе современных методов теории распознавания образов.

В данной работе применяется корреляционный метод обработки данных ЭЭГ совместно с методом распознавания образов для определения устойчивого и надежного критерия определения болезни пациента, а также повышения информативности ЭЭГ-исследования. В целом такой математический подход является универсальным, и применим для анализа большого числа заболеваний. Метод неоднократно зарекомендовал себя положительно при исследовании простых систем.

В качестве примера в статье рассмотрена болезнь Паркинсона.

Анализ исходных данных. Ограничения

ЭЭГ представляет собой запись усиленных специальными усилителями электрических потенциалов. Потенциалы снимаются одновременно с 18-ти датчиков, расположенных в разных точках скальпа. Числовые данные ЭЭГ фиксируются последовательно через равные промежутки времени Dt =h .

Рассмотрим особенности, связанные с методиками записи, и возможности применения математического аппарата для анализа и расшифровки данных ЭЭГ.

Поскольку ЭЭГ сигналы имеют сложную структуру, образованную электрическими импульсами различной амплитуды и регулярности, поступающими от разных отделов головного мозга [1-6], записи ЭЭГ можно рассматривать как случайные шумы электрического потенциала работы головного мозга.

Без учета дискретизации величины потенциала - преобразования аналог – цифра, будем считать, что запись ЭЭГ по каждому из 18 каналов является случайным процессом с непрерывным состоянием и дискретным временем, а запись ЭЭГ в целом – векторным случайным процессом.

Предполагается, что запись ЭЭГ производилась на достаточно большом временном интервале при стабильном состоянии пациента. Для дальнейшей компьютерной обработки выбирается отрезок записи ЭЭГ со случайным по времени началом. Информация о состоянии пациента на данном отрезке ЭЭГ, при достаточной длине последнего, не зависит от начала выбираемого отрезка.

Данные ограничения позволяют выбрать в качестве модели ЭЭГ стационарный в широком смысле случайный процесс, характеризующийся тем, что совместная плотность распределения его сечений при t₁ и t₂ не изменяется при сдвиге его временных аргументов (что соответствует изменению начала обрабатываемого отрезка ЭЭГ) на одинаковую произвольную величину t₁= k·h, k =...,-2,-1,0,1,2,....

f(t₁, t₂; x¹, x²) = f(t₁+ t₁, t₂ + t₁; x¹,x²).

Иначе, совместная плотность распределения двух сечений процесса не зависит от того, в какие моменты времени t₁, t₂рассматриваются сечения исследуемого процесса, а зависит лишь от сдвигов t = t₂- t₁ между этими сечениями. Заметим, что моменты времени t₁, t₂принимают дискретные значения.

Другие характеристики случайного, стационарного в широком смысле, процесса хорошо описаны в литературе, например в [7].

Поскольку в данной работе рассматриваются записи ЭЭГ, проводимые при постоянных условиях (имеются в виду коэффициент усиления k > 0 сигнала в усилителе, величина электрического сопротивления контакта датчика с кожей и т.д.), но, возможно, различных при записях потенциалов с разных датчиков, то одному и тому же состоянию пациента могут соответствовать различные записи ЭЭГ. В связи с изложенным желательно определить такую характеристику ЭЭГ, которая однозначно соответствовала бы состоянию пациента и была бы достаточно информативной для решения исходной задачи.

Для стационарного в широком смысле случайного векторного процесса x(t) квадратная матрица (в рассматриваемом случае размером 18х18) нормированных ковариационных функций (последовательностей)

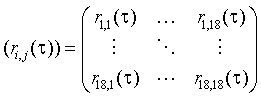
где

является не зависящей от коэффициентов усиления k_i> 0, характеристикой процесса. Нормированные корреляционные функции инвариантны относительно изменения начала отсчета и масштаба, т.е. преобразования y(t) = kx(t) + c векторного стационарного случайного процесса x(t), k = (k₁, …, k₁₈), c = (c₁, …, c₁₈)^T.

Достаточность информативности нормированных корреляционных функций определяется качеством решения исходной задачи.

Поскольку запись ЭЭГ представляет собой реализацию случайного процесса с неизвестными характеристиками, то вместо самих характеристик будем использовать их выборочные оценки.

В работе предлагается проводить обработку записей ЭЭГ в два этапа. На первом этапе по записям ЭЭГ строятся оценки нормированных корреляционных функций. На втором – производится обработка оценок этих функций.

Для решения исходной задачи, а именно, диагностики болезни Паркинсона, была использована экспериментальная выборка одного из 18-ти отведений ЭЭГ, а, именно, сигналов О2 – А2, соответствующих Международной схеме отведений ''10 - 20%'' [3] как для больных, так и для здоровых пациентов.

На первом этапе обработки по записям ЭЭГ строятся следующие оценки.

За несмещенную оценку среднего значения М[x] = m в рассматриваемом отведении принимаем

где X_t – последовательно полученные измерения величины сигнала в отведении ЭЭГ. Поскольку здесь и далее рассматривается сигнал только одного отведения, то номер отведения в обозначениях не указывается.

За оценку ковариационной последовательности М(x(t)-m)(x(t+ih)-m) = R(ih), i =0,1,... принимаем вектор размерности m с координатами

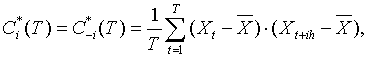
За оценку нормированной корреляционной последовательности r(t) принимаем вектор с координатами

(1)

Суммируя вышеизложенное, в качестве характеристики конкретной ЭЭГ для дальнейшего рассмотрения принимаем вектор y размерности m с координатами y_i, определенными в (1)

y = (y₁, y₂,…, y_m)^T. (2)

Вектор (2) содержит в сжатой форме информацию, имеющуюся в записи сигнала одного отведения ЭЭГ.

Постановка задачи. Оптимальная разделяющая гиперплоскость

Содержательная постановка задачи состоит в следующем. Имеется обучающая выборка, состоящая из a здоровых и b больных пациентов. Каждому здоровому пациенту провели запись ЭЭГ и вычислили вектор yⁱ, i=1,...,a, размерности m. Таким образом получили множество векторов

Y_a : y¹, …, y^a. (3)

Аналогично для больных пациентов получили множество векторов

(4)

Для пациента, обследуемого с целью выявления здоров он или болен, определили, аналогично, вектор Y_e.

Нужно выработать решающее правило, по которому на основе обучающей выборки можно определить, здоров или болен обследуемый пациент.

Поскольку множество векторов определяется по реализациям случайных процессов, то данная задача относится к классу задач обучения распознаванию образов в стохастической постановке.

Подобные задачи были сформулированы в конце 50-х годов 20-го века, и к настоящему времени их теория достаточно широко и подробно изложена в монографиях и статьях [8,9]. Поэтому остановимся только на кратком изложении некоторых, наиболее актуальных аспектах задачи.

Далее будем рассматривать только линейные решающие правила обучения распознаванию образов, основой для выработки которых является построение гиперплоскости в евклидовом пространстве E^m, разделяющей два конечных множества векторов (3) и (4).

Определение. Два конечных множества векторов: множество и разделимы гиперплоскостью, если существуют такой единичный j, и такое число c, что для любого вектора справедливо неравенство

а для любого вектора ¾ неравенство

Определим для любого единичного вектора j две величины с₁(j) и с₂(j):

(5)

(6)

Согласно определению величин с₁(j) и с₂(j) всегда справедливы неравенства

i=1, 2, …, a,

j=1, 2, …, b.

Ясно, что если

то пара 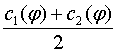определяет гиперплоскость

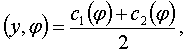
разделяющую множество Y от множества .

Заметим, что функции с₁(j) и с₂(j) непрерывны. Поэтому из существования одной гиперплоскости, разделяющей два конечных множества векторов Y и , следует существование целого множества гиперплоскостей, разделяющих Y и .

Будем выделять из множества разделяющих гиперплоскостей оптимальную.

Определение. Назовем оптимальной разделяющей гиперплоскостью такую разделяющую гиперплоскость, которая определяется парой: единичным вектором , доставляющим максимум функции

(7)

и числом

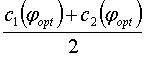(8)

Оптимальная разделяющая гиперплоскость, разделяя два множества векторов и , максимально от них удалена.

Для построения оптимальной разделяющей гиперплоскости рассмотрим все возможные разности

(9)

Вектор обладает свойством [9]

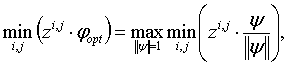(10)

поэтому он коллинеарен минимальному по модулю вектору , для которого выполняется неравенство

Отыскать вектор можно, максимизируя квадратичную форму

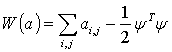(11)

(12)

в положительном квадранте .

В соответствии с выражениями (5) – (12) имеются алгоритмы для определения оптимальной разделяющей гиперплоскости [8,9]. По одному из них написана компьютерная программа в системе MATLAB и проведено моделирование по реальным записям ЭЭГ.

Результаты моделирования по определению оптимальной разделяющей гиперплоскости

По обучающей выборке, содержащей пять записей ЭЭГ здоровых пациентов и шесть записей ЭЭГ пациентов с болезнью Паркинсона, для каждой записи для сигнала О2 -- А2 ЭЭГ, записанного в течение 45с реального времени с дискретностью по времени h=0,01с, построен вектор y размерности 30 оценки нормированной корреляционной последовательности (1). Значения векторов ЭЭГ для здоровых и больных пациентов, вошедших в обучающую выборку, приведены, соответственно, в таблицах 1 и 2.

Таблица 1

Значения векторов оценок нормированной корреляционной последовательности для здоровых пациентов

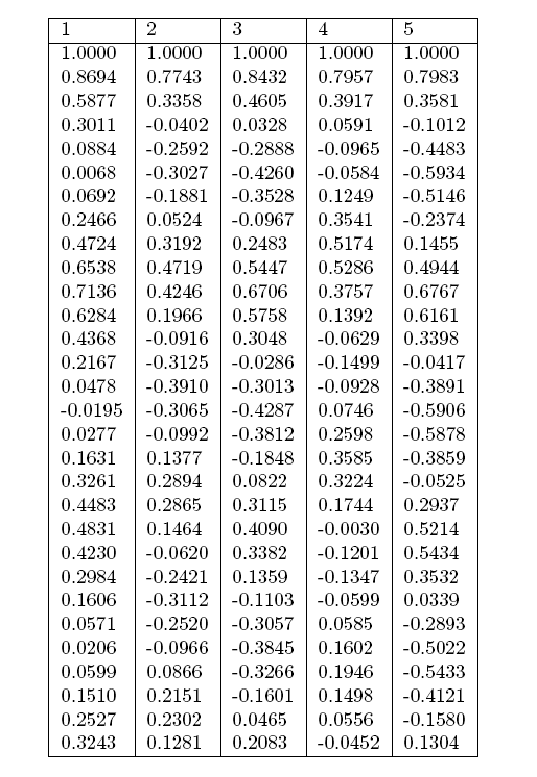
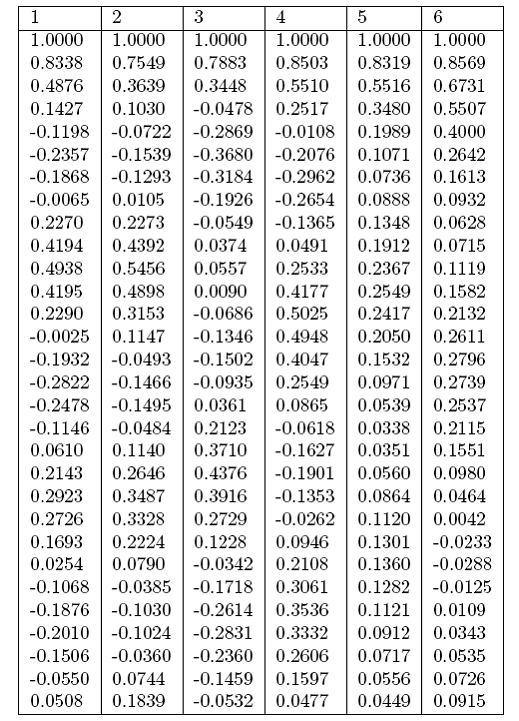
Таблица 2

Значения векторов оценок нормированной корреляционной последовательности для пациентов с болезнью Паркинсона

Оптимальная гиперплоскость, разделяющая множество векторов Y, соответствующее здоровым пациентам, от множества векторов , соответствующего больным, описывается уравнением

где

(0.; 0.0658; -0.0017; -0.2358; -0.3437; -0.2527; -0.0219; 0.2318; 0.4008; 0.4080; 0.2736; 0.0906; -0.0740; -0.1874; -0.1899; -0.0637; 0.1127; 0.2316; 0.2597; 0.2153; 0.1286; 0.0482; 0.0009; -0.0325; -0.0575; -0.0525; -0.0181; 0.0175; 0.0424; 0.0657)^T.

Минимальные расстояния от векторов множества и множества до оптимальной разделяющей гиперплоскости составляют 0.1462. На этом расстоянии находятся векторы и .

Значения промежуточных величин для определения оптимальной разделяющей гиперплоскости составляют

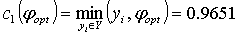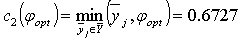В пространстве Е^m по обучающей выборке определяется оптимальная гиперплоскость, разделяющая множество векторов, соответствующих здоровым пациентам, от множества векторов, соответствующих больным. Для установления диагноза обследуемого пациента нужно определить вектор y размерности m, координатами которого являются оценки нормированной корреляционной последовательности (1).

Если для вектора Y_e, определенного для вновь обследуемого пациента, выполняется одно из условий

1) ,

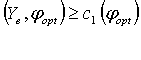то принимается решение "Обследуемый пациент здоров". Если

2) ,

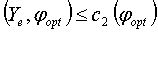то принимается решение "Обследуемый пациент болен". Если же

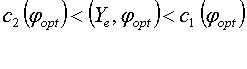
то выполняется дополнительное исследование.

Сначала полученный вектор Y_e включается во множество векторов, соответствующих здоровым пациентам. Определяется оптимальная гиперплоскость, разделяющая новое множество векторов {Y, Y_e} здоровых пациентов от множества векторов для больных . Вычисляется минимальное расстояние от векторов {Y, Y_e} до разделяющей гиперплоскости.

Далее полученный вектор Y_e включается во множество векторов, соответствующих больным пациентам. Определяется оптимальная гиперплоскость, разделяющая множество векторов {Y} здоровых пациентов от множества векторов для больных , и вычисляется минимальное расстояние от векторов {Y} до новой разделяющей гиперплоскости.

Если расстояние от множества {Y,Y_e} до гиперплоскости, полученной в первом случае, будет больше, чем расстояние от множества до гиперплоскости, полученной во втором случае, то принимаем решение, что пациент здоров. В противном случае принимаем решение, что пациент болен.

Моделирование показало высокое качество разделения векторов, оценивающих нормированные корреляционные функции, на два класса, соответствующих больным и здоровым пациентам. Это подтверждает достаточность информативности нормированных корреляционных функций при решении задач диагностики.

Выводы

Решена задача диагностики состояния центральной нервной системы человека по записям ЭЭГ как задача обучения распознавания образов в стохастической постановке. Общее решение подтверждено примером диагностики болезни Паркинсона.

Создан алгоритм сжатия информации, обеспечивающий качественное решение задач диагностики.

Для решения задач диагностики состояния центральной нервной системы человека на основе записи его ЭЭГ предлагается предварительно вычислить значения векторов (оценок элементов матрицы нормированных корреляционных функций) для каждого пациента, включенного в обучающую выборку и определить разделяющую пациентов на две группы гиперплоскость.

Для обследуемого пациента по его записи ЭЭГ предлагается вычислить значение вектора оценок элементов матрицы нормированных корреляционных функций и определить, к какой группе (больных или здоровых)отнести пациента.

Литература

1. Беритов И.С. Структура и функции коры большого мозга. М.: Наука. 1969.

2. Осовец С.М., Гинзбург Д.А., Гурфинкель В.С. и др. Электрическая активность мозга: механизмы и интерпретация. // Успехи физических наук, 1983, т. 141., вып. 1., с. 103 - 150.

3. Щекутьев Г.А. Методика электроэнцефалографии. В кн.: Нейрофизиологические исследования в клинике. М.: Антидор, 2001, с. 16-24.

4. Болдырева Г.Н. Стабильность спектрально-когерентных характеристик ЭЭГ человека. // Успехи физиологических наук, 1994, т.25, № 1, с. 68-104.

5. Воронов В.Г. Выявление статистически значимых особенностей в частотных спектрах электроэнцефалограмм. // Труды YIII Международной конференции" Новые информационные технологии в медицине и технологии". Украина, Гурзуф, 2000, c. 244-245.

6. Электрофизиологическое исследование стационарной активности в головном мозге. М.: Наука, 1983.

7. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. М.: Наука. 1969, 383с.

8. Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. М.: Наука, 1974, 416с.

9. Вапник В.Н. Восстановление зависимостей по эмпирическим данным. М.: Наука 1979, 448с.