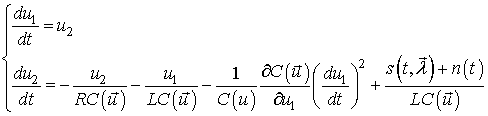Идентификация сигналов изображения робастными системами со стохастической накачкой

В. И. Неволин, М. Б. Меренков, Д. В. Иванеев, М. А. Зуйкова

Южно-Уральский государственный университет

Получена 16 января 2013 г.

Аннотация. В статье рассматриваются вопросы методологии робастных методов идентификации сигналов с неизвестными параметрами, в том числе сигналов изображения, например, для космического радиозондирования, при их приеме в условиях действия мощных аддитивных помех. Используется непараметрический статистический подход, базирующийся на выборочных распределениях наблюдений. По методу робастной нелинейной фильтрации проводится синтез схем робастных фильтров, а идентификация (фильтрация и обнаружение) сигналов путем построения робастных парциальных систем. Приведено обоснование физического повышения помехоустойчивости робастных систем за счет явления энергетических преобразований при стохастической автоматической накачке от сопутствующих аддитивных помех. Проведено моделирование, отмечающее повышение помехоустойчивости по сравнению с согласованной фильтрацией.

Ключевые слова: робастный метод, нелинейная фильтрация, численное моделирование, стохастическая автоматическая накачка.

Abstract: The problems of methodology of robust systems of the identification of signals with unknown parameters as well as the identification of image signals under the conditions of powerful additive hindrances, e.g. for space radiosonde observation, are dealt with in the article. The nonparametric stochastic approach based on selective distributions of observations is used here. The synthesis of the schemes of robust filters is carried out by the robust nonlinear filtration method, and the identification (filtration and detection) of signals – by constructing robust partial systems. The basis of physical increase of robust systems’ noise stability due to the phenomenon of power transformations under the conditions of stochastic automatic rating from attendant additive hindrances is laid down in the paper. The results of the conducted simulation show the essential increase of noise stability in comparison with the coordinated filtration.

Keywords: robust methods, nonlinear filtering, numerical modeling, stochastic pumping.

В статье рассматриваются вопросы приема и обработки (идентификации) сигналов с неизвестными параметрами на фоне помех и синтеза робастных систем. Решения рассматриваемых задач проводятся с помощью разработанного в [1] метода робастной нелинейной фильтрации. Этот метод базируется на теории робастных статистик, методе функции влияния Хэмпбела [2] и использует согласно [1]: условно-параметрический подход (параметризацию) в непараметрических задачах, робастный вариант леммы Неймана-Пирсона, критерий согласованности, а также оптимальный и слабый робастные критерии непараметрического обнаружения. Проводится обоснование физического смысла нелинейной робастной фильтрации на основе общих принципов энергетических преобразований в параметрических динамических нелинейных систем, так как основой повышения помехоустойчивости в робастных системах обработки сигналов при действии помех является явление энергетических преобразований в нелинейных системах, когда помехи выполняют функции генератора стохастической накачки. Особенности синтеза и своеобразие структур нелинейных робастных систем и новые результаты показаны на примере задач при приеме на фоне шумов: а) обнаружение и фильтрация видеоимпульсов, б) обнаружение и фильтрация радиоимпульсов [3,4].

Введение

Согласно [1] синтез робастных обнаружителей производится первоначально по критерию согласованности (синтез базовой структуры в виде типа и порядка линейного дифференциального уравнения), а затем основной и завершающий синтез нелинейного уравнения. Первоначальный синтез робастного алгоритма обработки производится при использовании соответствующего опорного сигнала, а завершающий - выполняется на основе слабого робастного критерия непараметрического обнаружения. Этот критерий разработан в [1] на основе условия инвариантности для уравнения Фоккера-Планка-Колмогорова (ФПК) и может записан в виде

(1)

где одномерная нестационарная плотность распределения вероятностей (ПРВ) состояния нелинейной системы в соответствующем уравнении ФПК

Критерий (1) – математическая база метода нелинейной робастной фильтрации. Физическая же основа – это энергетические преобразования в параметрических нелинейных динамических системах.

Большинство применений параметрических устройств предполагают гармонические воздействия, как для входного сигнала, так и сигнала накачки. В информационных системах при действии помех функционирование более близко к импульсному режиму. Рассмотрим состояние нелинейной емкости, находящейся под воздействием информационного сигнала и сигнала генератора накачки (рис. 1). На рис. 1 приведена нелинейная емкость и обозначено: FP– фильтр-пробка накачки, FS– фильтр-пробка сигнала, – нелинейный конденсатор, – источник напряжения сигнала, – генератор накачки.

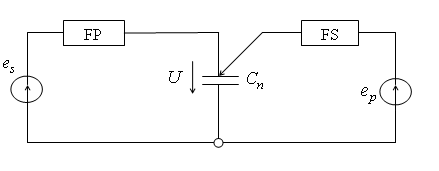
Рис. 1. Эквивалентная схема включения нелинейной емкости

При определении состояния в схеме по рис. 1 для импульсных режимов можно выбрать сигнал генератора накачки в виде периодической последовательности прямоугольных импульсов достаточно большой скважности с некоторой частотой повторения . Тогда сигнал накачки можно записать в виде следующего гармонического ряда

(2)

При этом информационный сигнал для получения компактных и наглядных энергетических соотношений можно взять также гармоническим типа

(3)

При стохастической накачке (2) будет представлять короткие квазипериодические последовательности . Тогда для некоторых последовательностей для (2), (3) будет

(4)

т. е., для некоторых компонент гармонические составляющие накачки будут с частотой информационного сигнала. Так как можно записать, что то для частот по (4) составляющие тока в емкости характеризуют активную нагрузку, мощность в которой

(5)

Суммирование в (5) производится по последовательностям . При значениях начальных фаз накачки активная мощность согласно (5) становится отрицательной

т. е. поступает из параметрической емкости в источник информационного сигнала. Вследствие этого и происходит увеличение энергии сигнала (усиление сигнала) за счет энергии стохастической накачки. В робастных стохастических системах поворот фазы на осуществляется вследствие операций идеального дифференцирования и инвертирования.

Для финитных информационных сигналов можно провести разложение в гармоническом базисе, но при этом робастные системы будут сложнее, например, их объединение [5].

Алгоритмически нелинейные стохастические системы следуют из робастных алгоритмов синтеза соответственно как синтез оптимальных линейных алгоритмов можно получить на основе байесовой теории статистических решений. Причем при линеаризации робастные свойства нелинейных систем вырождаются и реализуется только линейная, в частном случае – оптимальная, фильтрация.

Обнаружение и фильтрация видеоимпульсов

Непараметрические обнаружение и идентификацию сигналов на фоне шума могут быть сформулированы так, что наблюдаются

, , (6)

где – сигнал с неизвестными параметрами (нестационарный случайный процесс с произвольным распределением (НСППР), но частично заданными статистическими характеристиками), (0 – отсутствие сигнала (простая нулевая гипотеза ) и 1 – его наличие (непараметрически заданная гипотеза –)), а при (6) являются задачами идентификации, – широкополосный шум с некоторым распределением, – интервал наблюдения.

Данная задача, т. е., обнаружение и идентификация видеосигналов, включающая как обнаружение, так и совместную оценку неизвестных их параметров, выполняется на основе методологии [1]. При этом для обработки наблюдений (6) на основе явления стохастической накачки используется нелинейная робастная динамическая система не ниже второго порядка.

Для формирования опорной функции следует принять, например, условие квазиоптимального обнаружения данного информационного сигнала. Тогда, согласно [1], для достаточно широкого класса низкочастотных сигналов опорный сигнал будет соответствовать импульсной характеристике квазиоптимального линейного фильтра (КЛФ), как минимум, второго порядка.

Таким образом, при использовании в качестве системы второго порядка одиночного колебательного контура (ОКК) Г-образного звена, нелинейный алгоритм обработки может быть записан в виде стохастического нелинейного дифференциального уравнения (переменная состояния обозначена напряжением на емкости ОКК) как

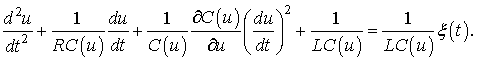(7)

Здесь R, – сопротивление и нелинейная ёмкость ОКК, и индуктивность может быть принята как постоянная.

Уравнение (7) может быть записано в каноническом виде системы стохастических дифференциальных уравнений первого порядка

(8)

Система уравнений (8) описывает многомерный марковский процесс и тогда для окончательного структурно-параметрического синтеза, в том числе для определения параметрических зависимостей можно применить слабый критерий робастного обнаружения (1) в виде (при )

. (9)

Здесь – нестационарная ПРВ в соответствующем уравнении ФПК, который можно составить для марковского диффузионного процесса по системе уравнений (8).

Условия (9) соответствуют выполнению для коэффициентов сноса соответствующего уравнения ФПК следующих соотношений

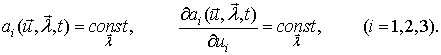(10)

Соотношения (10) являются условиями статистической непараметрической нечувствительности алгоритма обработки в данной задаче при наблюдении (6).

Из систем уравнений (8,10) можно получить следующие выражения для коэффициентов сноса:

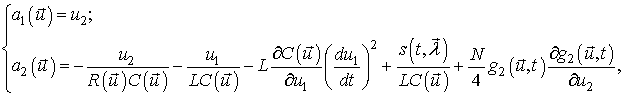(11)

где

Используя (10), (11) согласно методике [1] можно получить нелинейные зависимости в виде

(12а)

(12б)

Здесь – постоянная величина, k₂– коэффициент пропорциональности.

На рис. 2 приведена согласно (8) принципиальная электрическая схема робастного фильтра.

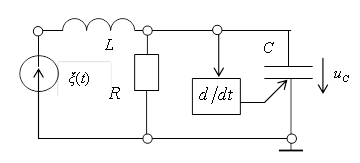
Рис. 2. Принципиальная схема робастного нелинейного фильтра

Для этого фильтра было проведено моделирование, результаты – отфильтрованная текущая реализация на выходе которого, приведены на рис. 3 (использовался нормальный шум – БГШ). Данное моделирования проводилось при отношении сигнал/шум около -6дБ (или 4дБ в полосе соответствующего согласованного линейного фильтра (СФ)). Кроме того, согласно приведенному выше материалу, на базе робастного фильтра реализовывалась система парциальных каналов с функциональным сглаживанием на входе – для стохастической устойчивости решений [5].

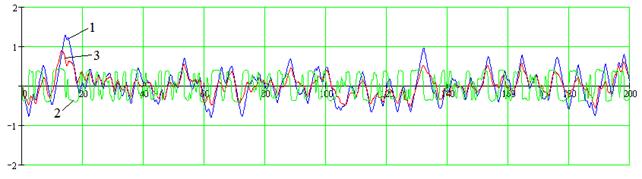
Рис.3. Реализации отфильтрованных случайных процессов

На рис. 3 приведены реализации отфильтрованных наблюдений как в парциальном канале для нелинейного фильтра (НФ) (8) – кривые 1,2, так и для сравнения в соответствующем КЛФ (кривая 3). При этом кривая 1 – это состояние НФ, а кривая 2 – производная этого состояния (накачка). Отклик в НФ больше отклика КЛФ примерно на 4-7дБ, что и является основой повышения помехоустойчивости в робастных фильтрах. Для обнаружителя видеоимпульса на фоне белого гауссового шума (БГШ) робастной системой парциальных каналов также исследованы путем статистического моделирования рабочие характеристики. С целью адекватного сопоставления результатов моделирования с СФ наблюдение (6) предполагалось для видеоимпульса с прямоугольной огибающей и известными параметрами. Однако при этом использовалось некогерентное обнаружение как более реальное в практических приложениях. В уравнениях (8) нелинейная емкость (рис. 2) зависит только от фазовой координаты и была принята в виде В эксперименте робастная система апробировалась в составе как 3-х, так и 4-х парциальных каналов с различными параметрами .Параметры линейного аналога системы (8) выбирались из условия квазиоптимальной фильтрации этим аналогом заданного прямоугольного униполярного импульса.Соответственно параметрам линейного аналога ориентировочно определялись и параметры нелинейной системы с их последующей вариацией при проведении эксперимента (при опыте принято: , , , ).

При моделировании были приняты параметры: L=2, C₂=0.5, R=2, A₀=0.5, – среднеквадратические БГШ при отношениях сигнал/шум в полосе соответствующего СФ (E – энергия сигнала, N₀ – интенсивность БГШ) и объеме выборки – .

Результаты статистического моделирование приведены в таблице вероятностей правильного обнаружения для вероятности ложной тревоги F=0.01, где обозначено: -парциальные каналы; НФ3, НФ4 - соответственно робастные системы из 3 и 4 каналов. Более полные результаты (рабочие характеристики обнаружения и соответствующие им гистограммы) показаны на рис. 4-8.

Таблица. Вероятности правильного обнаружения

1)	2)	3)	4)	5)НФ3	6)НФ4	7)КЛФ	8)СФ
0.92733	0.90276	0.85075	0.90014	0.9531	0.99968	0.98409	0.99158
0.26671	0.16825	0.27272	0.32043	0.37887	0.66318	0.46303	0.5120

Согласно таблице, на генеральных совокупностях помехоустойчивость обнаружителей при данной робастной обработке (НФ4) превышает для g₁ и g₂ как КЛФ (до 1.6дБ), так и СФ (около 1 дБ), тогда как в парциальных каналах помехоустойчивость хуже – до 10дБ. Этот эффект объясняется тем, что робастная парциальная обработка на основе явления стохастической накачки реализует в каналах как увеличение энергии сигнала, так и сохранение корреляции на сигнальных выборках и декорреляцию на шумовых выборках, обеспечивая этим для каналов синфазное суммирование для сигнала и противофазное – для помех. Согласно рис. 3 для временных реализаций (на малых выборках) в парциальных каналах при робастной обработке по сравнению с КЛФ имеет место увеличение сигнала (в отмеченной области) около (4-7)дБ. При усреднении (на генеральной совокупности) вследствие стохастичности накачки этот выигрыш уменьшается (в данном эксперименте согласно таблице до 1 дБ). Очевидно, что потенциальный предел повышения помехоустойчивости при робастной обработке и определяется выигрышем относительно согласованной фильтрации для малых (текущих) выборок. Однако однозначно оценить этот предел проблематично вследствие неизвестных закономерностей данного явления стохастической накачки.

Некоторые особенности робастной парциальной системы можно также отметить на анализе статистических результатов моделирования. А именно, по рис. 4, 5, где приведены рабочие характеристики обнаружения (РХ) соответственно для , и при , и рис. 6-8 – гистограммам согласно этим случаям и алгоритмам по обозначениям таблицы.

На рис. 4 изображены два семейства РХ для отношений сигнал/шум . Цифрами обозначены кривые по номеру столбца таблицы. Для обоих семейств следует, что помехоустойчивость 4-х канальной робастной парциальной системы больше согласованной фильтрации (СФ) примерно на 1.2 дБ, а квазиоптимальной линейной фильтрации (КЛФ) на 1.8дБ. Тогда как помехоустойчивость отдельных парциальных каналов, а также 3-х канальной робастной парциальной системы хуже КЛФ от 1 до 5дБ, причем у данной 3-х канальной парциальной системы проигрыш минимальный. Следует отметить, что качественный характер РХ обоих семейств подобен, однако, в семействах некоторые парциальные каналы меняются местами, что обусловлено нелинейным механизмом стохастической накачки в робастных сложных динамических системах.

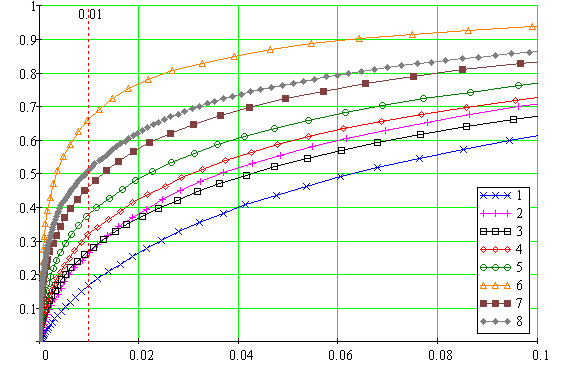
Рис. 4а. Рабочие характеристики для отношения сигнал/шум – g₁

Рис. 4б. Рабочие характеристики при g₂

На рис. 5 показаны РХ для g₁, но с в 2 раза меньшими значениями сигнала и шума. Таким способом реализовывалась меньшая степень нелинейностей систем. Нелинейный режим систем обусловливался, в основном, действием сигнала, а также большими выбросами шума, при этом РХ СФ и КЛФ не изменились. Вследствие того же эффекта меньшего влияния нелинейностей РХ остальных алгоритмов существенно сблизились, а РХ 4-х канального РФ несколько улучшилась, причем достаточно существенно для области малых ложных тревог, что и является, очевидно, спецификой подобного слабого нелинейного взаимодействия. Таким образом, уменьшение степени нелинейности приближает робастную систему к линейной, однако, как следует из эксперимента, любому нелинейному режиму присущи робастные свойства, причем даже с выраженными локальными областями. Это свойство может использовано, например, в РЛС с малыми вероятностями ложных тревог.

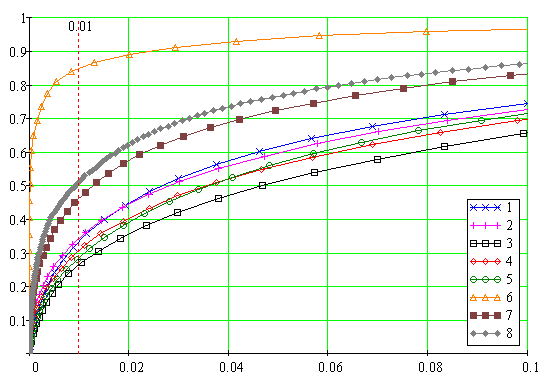
Рис. 5. Рабочие характеристики при g1, но в два раза меньшими значениями сигнала и шума

На рис. 6 приведены гистограммы для случая, когда сигнал/шум равен g₁ и в системе реализуются существенно нелинейные режимы. Как следует из рис. 6, нулевые гипотезы, особенно для парциальных каналов, фактически совпадают, а ненулевые различаются, причем для линейной обработки (КЛФ) они отличаются, естественно, только сдвигом, тогда как для 4-х канального РФ оценки плотности распределения вероятностей (ПРВ) имеют меньшие дисперсии при более меньшей (раза в полтора-два) дисперсии ненулевой гипотезы, что и является следствием синфазного объединения коррелированных сигнальных составляющих и противофазного подавления некоррелированных помеховых составляющих парциальной системы. Таким образом, робастные оценки могут быть эффективнее оптимальных, например, для данного эксперимента, примерно, на 1–2 дБ. Имеет место также смещение нулевой гипотезы, что, очевидно, может быть использовано для предварительной калибровки робастной системы.

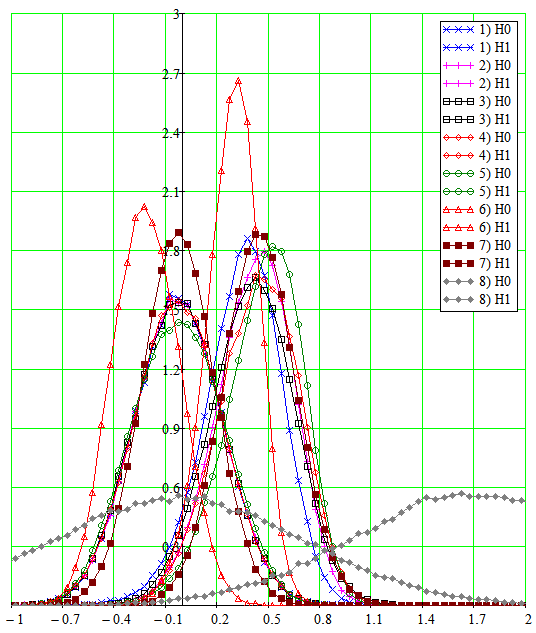
Рис. 6. Гистограммы для сигнал/шум= g₁

Гистограммы для случая большего отношения сигнал/шум, равном g₂, даны на рис.7. Особенности гистограмм такие же, как на рис. 6. Лишь несколько увеличился сдвиг ненулевой гипотезы. Сопоставление как РХ, так и гистограмм подтверждает, что робастные свойства нелинейных систем приемлемо сохраняются в относительно широком диапазоне использования нелинейных характеристик. Подобное качество робастных систем вкупе с главным свойством – более высокой помехоустойчивостью, чем известные оптимальные, предполагает их широкое практическое соответствующее применение.

Рис. 7. Гистограммы для сигнал/шум= g₂

Гистограммы для g₁и вдвое меньших уровнях сигнала и шума приведены на рис. 8. Качественные характеристики гистограмм подобны гистограммам по рис. 6,7, однако для данного более слабого (как отмечалось выше) нелинейного режима имеет место меньшая дисперсия нулевой гипотезы 4-х канальной робастной системы даже по сравнению с соответствующей ненулевой. Причем эта дисперсия ненулевой гипотезы 4-х канального НФ меньше дисперсий парциальных каналов. Отмеченные свойства достаточно наглядно характеризуют специфику синфазного и противофазного суммирования формирующихся коррелированных и некоррелированных совокупностей сигнальной и помеховой составляющих отклика парциальной робастной системы. Согласно рис.8 можно также отметить, что для парциальных составляющих обе гипотезы фактически совпадают при небольшом рассеянии для ненулевой гипотезы. Этим экспериментально и подтверждается (совместно с данными рис. 7 и других) отмеченное выше теоретическое предположение о вырождении робастных систем при линеаризации их в линейные и соответствующей нейтрализации явления стохастической накачки.

Таким образом, на основе приведенного материала, и прежде всего экспериментальных результатов, можно отметить, что непараметрические методы обработки статистических данных содержат, прежде всего, методологическую основу фильтрации помех как нелинейное взаимодействие мощных помех и полезного информационного сигнала. В большинстве случаях это взаимодействие приводит к подавлению сигнала помехами, однако, в некоторых системах, организованных соответственно, как например, когнитивных (высшей форме материи), имеет место увеличение энергии полезного информационного сигнала стохастической накачкой за счет энергии помех.

Для радиоимпульсов как периодических процессов параметрические энергетические преобразования проявляются более существенно, например, как в следующей задаче.

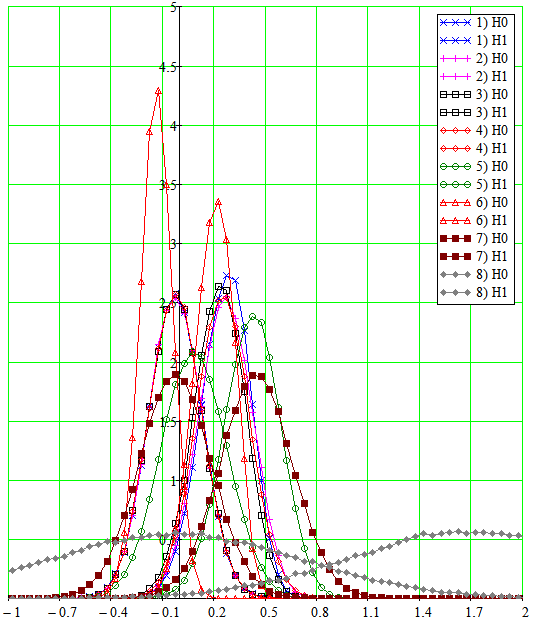
Рис. 8. Гистограммы для сигнал/шум=g₁ при вдвое меньшем уровне сигнала

Обнаружение и идентификация радиоимпульсов

Пусть на фоне равномерных шумов, как для (6), нужно провести фильтрацию радиоимпульса, распределение несущей частоты которого принадлежит некоторому ограниченному не параметризированному семейству в диапазоне частот Т. е. наблюдается действительный случайный процесс

(13)

Здесь – известный амплитудный множитель, определяющий мощность радиоимпульса; – случайная начальная фаза с произвольным распределением на интервале , – функция огибающей радиоимпульса, причем ; вектор известных параметров огибающей так, что множеству соответствующего эвклидова пространства, например, для прямоугольной огибающей и (соответственно начальное положение и длительность радиоимпульса).

Тогда аналогично предыдущей для данной непараметрической задачи нелинейный алгоритм обработки может быть записан в виде следующей системы стохастических нелинейных дифференциальных уравнений (переменные состояния системы обозначены напряжениями на емкости одиночного колебательного контура (ОКК) Г-образного типа и выходе фильтра низких частот (ФНЧ) 1-го порядка)

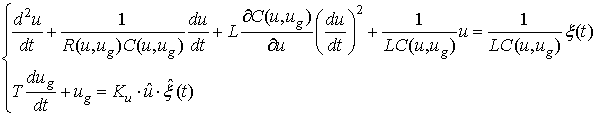(14)

Здесь – нелинейные соответственно сопротивление и ёмкость ОКК, и индуктивность может быть принята как постоянная, – сопряженные по Гильберту соответственно случайные процессы и (у спектральных составляющих, сопряженных по Гильберту функций, фазы запаздывают на 90⁰), , и – соответственно сопротивление и емкость интегрирующей электрической цепи первого порядка как ФНЧ, – коэффициент передачи умножителя.

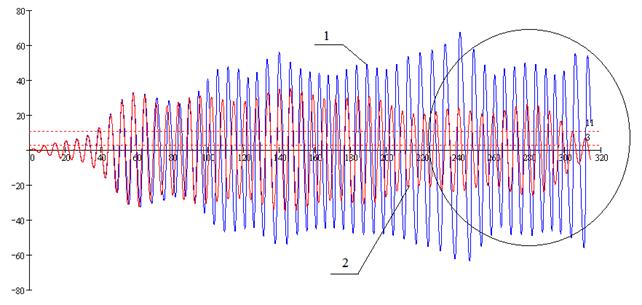
Рис. 9. Реализации узкополосных случайных процессов

Для оценки эффективности этого, уже адаптивного робастного фильтра, также по сравнению с соответствующим КЛФ, проведено моделирование только на малых выборках. При моделировании были приняты следующие базовые параметры: L=1, C₀=1, R₀=25, =3.3, T=30, при отношении сигнал/шум в полосе соответствующего согласованного фильтра , E – энергия сигнала, N₀ – интенсивность аддитивного БГШ.

Результаты моделирования приведены на рис. 9, где показаны реализации случайных процессов в робастном адаптивном (РФ) (кривая 1) и соответствующем квазиоптимальном линейном (КЛФ) (кривая 2) фильтрах. Из рисунка следует, что в момент окончания импульса выходная амплитуда в РФ примерно на 20 дБ превышает соответствующую амплитуду КЛФ, что и является результатом явления параметрических энергетических преобразований при стохастической накачке.

Эффективность метода нелинейной робастной фильтрации может быть также использована, например, для повышения четкости изображений при космическом радионаблюдении наземных объектов, являющихся двумерными и, как правило, протяженными. При этом дополнительно к показанной выше робастной нелинейной фильтрации можно применить новый тип сложных сигналов (некогерентных). А именно вместо широко используемых для энергетического накопления сложных сигналов с внутриимпульсной модуляцией типа, например, ЛЧМ сигналов (с линейной частотной модуляцией) и других подобных, следует применять робастные сигналы на основе [3], [4]. Как и ЛЧМ такие робастные сигналы также являются сложными, т. е. обладают эффектом энергетического накопления, однако имеют некогерентную структуру. Поэтому для них при зондировании протяженных целей при отражении и приеме реализуется некогерентное накопление, что приводит к существенно меньшему «разваливанию» обработанного сложного сигнала и этим повышается четкость изображений. Подобные робастные принципы обработки протяженных целей могут быть использованы и во многих других информационных системах, а не только при обработке изображений, например, в системах передачи информации с мультипликативными помехами. Вследствие дискретной структуры такого сложного сигнала будет существенно снижен, как на периодической структуре, эффект его подавления при многолучевом распространении.

Изложенный в данной статье (а также других авторских публикациях) материал по робастным системам обработки информационных сигналов (робастным информационным системам) имеет широчайшую практическую направленность. Поэтому, одно из возможных главнейших применений данных робастных информационных систем – это их использование в интеллектуальных системах, важнейшее качество которых заключается в функционировании в условиях высокой априорной неопределенности, в том числе мощных помех. Энергетически экономные робастные парциальные системы, так и как многоканальная и многомерная обработка, очевидно, и являются некоторым аналогом мыслящих (накапливающих, эвристических и обобщающих) биологических субстанций и могут использованы для создания высокоэффективных вычислительных структур нового поколения.

Выводы

1. Повышение помехоустойчивости робастных методов обработки сигналов на фоне помех, а также фильтрации, обусловлено действием стохастической автоматической накачки за счет этих сопутствующих помех (шума).

2. Получены робастные структуры обнаружителей в таких широко распространенных в радиотехнических системах практических задачах как обнаружение видеоимпульсов и их некогерентных последовательностей, обнаружение радиоимпульсов с небольшими базами и неизвестными частотами, а также их некогерентных и несинхронных пачек.

3. Приведенные результаты и моделирования полученных робастных систем показывают, что увеличение помехоустойчивости по сравнению с известными структурами может составить (10 – 20)дБ и более.

4. Робастная обработка совместно с новыми сложными некогерентными сигналами может повысить четкость радиолокации протяженных целей и помехоустойчивость систем передачи информации для мультипликативных помех.

5. Робастные парциальные информационные системы могут быть использованы для создания высокоэффективных интеллектуальных и вычислительных систем нового поколения.

Литература

1. Неволин В.И. Робастные информационные системы. Методы синтеза и анализа. — М.: Радио и связь, 2008. — 312 с.: ил.

2. Хьюбер Дж. Робастность в статистике. Пер. с англ. М.: Наука, 1984.

3. Неволин В.И., Неволин В.В. Способ фильтрации и обнаружения флуктуирующей пачки радиоимпульсов. Патент на изобретение № 2459350 от 20.06.2012.

4. Неволин В.И., Перунов Ю.М., Бородин А.М., Дмитриев В.Г. Устройство обнаружения радиоимпульсов со случайной фазой. Патент на изобретение №2333625 от 11.08.2008.

5. Неволин В.И., Неволин В.В. Способ фильтрации и обнаружения импульсных сигналов робастной системой парциальных каналов. Заявка на изобретение(находится на стадии предварительной экспертизы в Госреестре изобретений).