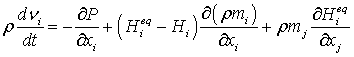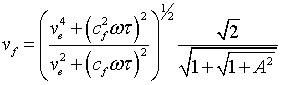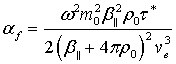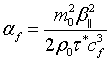УДК 53.098, 538.955
влияние постоянного МАГНИТНОГО ПОЛЯ нА РаспрОстраненИе УЛЬТРАЗВУКА В МАГНИТНЫХ ЖИДКОСТЯХ
И. Э. Овчинников
Московский государственный университет приборостроения и
информатики
Получена 15 января 2013 г.
Аннотация. Рассмотрено распространение гидродинамических волн малой амплитуды в магнитной жидкости при учете процесса релаксации магнитного поля к своему равновесному значению. Получены выражения для фазовых скоростей и коэффициентов поглощения быстрой магнитогидродинамической волны и для волны альфвеновского типа при распространении параллельно магнитному полю. Показано, что из теоретического анализа экспериментальных данных по скорости ультразвука в магнитных наножидкостях на основе воды и керосина следует: коэффициенты поглощения волн данных типов практически стремятся к нулю при длительном воздействии однородного постоянного магнитного поля.
Ключевые слова: магнитная жидкость, магнитное поле, ультразвук, наночастицы, магнетит.
Abstract: The propagation of hydrodynamic waves of small amplitude in magnetic fluid was considered with taking into account the process of relaxation of the magnetic field to its equilibrium value. The expressions for phase velocities and absorption coefficients were obtained for the fast magnetohydrodinamic wave and the Alfven type wave under propagation in parallel to magnetic field. It was shown by the theoretical analysis of the experimental data on the ultrasonic velocity in magnetic nanofluids based on water and kerosene should: absorption coefficients of these types of waves almost vanish by prolonged exposure of the homogeneous static magnetic field.
Key words: magnetic fluid, magnetic field, ultrasonics, nanoparticles, magnetite.
1.Введение
В [1] был предложен метод измерения профиля скорости среды по доплеровскому сдвигу для ультразвукового диапазона. Впоследствии данный метод был применен для исследования магнитных жидкостей [2]. Для применения данного метода должно быть определено значение скорости ультразвука с хорошей точностью, но эксперименты выявили значительные изменения скорости ультразвука в зависимости от времени нахождения магнитных жидкостей в магнитном поле [3]. Для объяснения данных явлений были применены различные теоретические модели магнитных жидкостей [4]. Модель магнитной жидкости с вмороженной намагниченностью [5] показала количественное соответствие с экспериментальными данными по анизотропии скорости распространения ультразвука в магнитной жидкости после длительного воздействия однородного стационарного магнитного поля на измерительную ячейку [4,6,7]. Целью данной работы является выявление особенностей распространения ультразвука в магнитных наножидкостях от времени воздействия однородного постоянного магнитного поля.
2. Распространение звука в магнитной жидкости с учетом релаксации магнитного поля
В [8,9] получена система
уравнений для непроводящей магнитной жидкости с учетом теплопроводности,
вязкости среды и времени ![]() установления
равновесного значения напряженности магнитного поля. Для детального рассмотрения
влияния времени релаксации
установления
равновесного значения напряженности магнитного поля. Для детального рассмотрения
влияния времени релаксации ![]() на распространение
звука в настоящей работе не учитываются теплопроводность и вязкость, поэтому
система уравнений состоит из
на распространение
звука в настоящей работе не учитываются теплопроводность и вязкость, поэтому
система уравнений состоит из
уравнения непрерывности
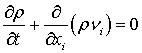
уравнения сохранения импульса
уравнения эволюции удельной
намагниченности ![]() ,
,
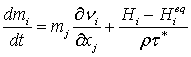
Так же были применены магнитостатические уравнениями Максвелла:
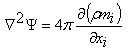
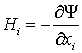
где ![]() -
скалярный потенциал магнитного поля,
-
скалярный потенциал магнитного поля, ![]() - гидродинамическая
скорость,
- гидродинамическая
скорость, ![]() - плотность магнитной жидкости,
- плотность магнитной жидкости, ![]() - намагниченность, равновесное значение магнитного
поля
- намагниченность, равновесное значение магнитного
поля ![]() .
.
Для полноты системы уравнений (1) следует
ввести зависимости удельной свободной энергии ![]() от температуры
от температуры ![]() , компонент удельной намагниченности
, компонент удельной намагниченности ![]() и плотности магнитной жидкости
и плотности магнитной жидкости ![]() . Распространение звука слабо возмущает
состояние данной термодинамической системы, поэтому около положения равновесия разложение
для удельной свободной энергии записывается в следующем виде [8]:
. Распространение звука слабо возмущает
состояние данной термодинамической системы, поэтому около положения равновесия разложение
для удельной свободной энергии записывается в следующем виде [8]:
![]() , (2)
, (2)
где ![]() -
термодинамический параметр, диагональный тензор с компонентами
-
термодинамический параметр, диагональный тензор с компонентами ![]() ,
,![]() ,
определяющий магнитоупругие свойства магнитной жидкости,
,
определяющий магнитоупругие свойства магнитной жидкости, ![]() - компоненты невозмущенной удельной
намагниченности,
- компоненты невозмущенной удельной
намагниченности, ![]() - плотность
невозмущенной магнитной жидкости.
- плотность
невозмущенной магнитной жидкости.
Давление определяется через удельную свободную энергию
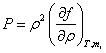
Считаем, что покоящаяся магнитная
жидкость находится в бесконечном объёме во внешнем магнитном поле c напряжённостью ![]() , направленном вдоль оси
, направленном вдоль оси ![]() . Невозмущённое состояние описывается
уравнениями
. Невозмущённое состояние описывается
уравнениями
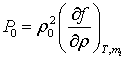 (3)
(3)
![]()
Распространение волн исследуется в
линейном приближении, поэтому переменные величины представляются в виде сумм
невозмущённого и возмущённого слагаемых ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
Использование стандартных методов линеаризации приводит к следующей системе уравнений (далее штрихи не пишем):
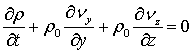
![]()
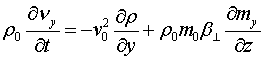
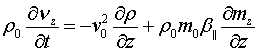 (4)
(4)
![]()
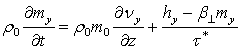
![]()
где ![]() -
скорость звука в магнитной жидкости без магнитного поля.
-
скорость звука в магнитной жидкости без магнитного поля.
Поскольку в рассматриваемой системе учитывается диссипативный процесс,
то волновой вектор представлен в
комплексном виде [10]: ![]() , где
, где ![]() - волновое число,
- волновое число, ![]() -
коэффициент поглощения,
-
коэффициент поглощения, ![]() - мнимая единица.
- мнимая единица.
Используя магнитостатические
уравнения Максвелла и пропорциональность для возмущений переменных ![]() , получаем из (1-4) систему уравнений в
матричной форме [11]
, получаем из (1-4) систему уравнений в
матричной форме [11]
![]() (5)
(5)
где
![]() -
вектор состояния,
-
вектор состояния, ![]() - круговая частота.
- круговая частота.
![]() Ненулевые элементы матрицы
Ненулевые элементы матрицы ![]() перечислены
ниже
перечислены
ниже
![]() ,
, ![]() ,
, 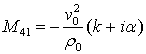 ,
, ![]() ,
, ![]() ,
,
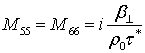 ,
, 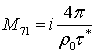 ,
, 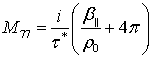 .
.
Приравнивая к нулю определитель матрицы (5), получаем уравнение, которое, очевидно, является произведением трех дисперсионных уравнений
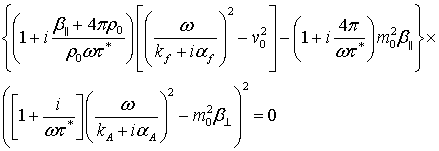
Приравнивая к нулю первый
сомножитель получаем дисперсионное уравнение, которое определяет быструю магнитогидродинамическую
волну с распространением возмущений ![]() ,
,![]() и
и ![]() . Решениями
дисперсионного уравнения являются выражения для величины фазовой скорости
. Решениями
дисперсионного уравнения являются выражения для величины фазовой скорости ![]() и коэффициента поглощения данной
волны
и коэффициента поглощения данной
волны
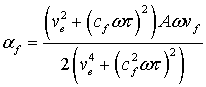 ,
(7)
,
(7)
где
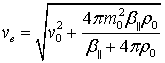 (8)
(8)
![]() (9)
(9)
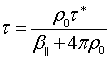 (10)
(10)
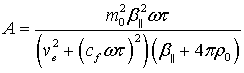 (11)
(11)
безразмерный параметр ![]() стремится к нулю при
стремится к нулю при ![]() и
и ![]() , а в
максимуме при
, а в
максимуме при ![]() равен
равен ![]() , и для приводимых в настоящей статье
экспериментальных данных, его численное значение в максимуме
, и для приводимых в настоящей статье
экспериментальных данных, его численное значение в максимуме ![]() . Максимальное значение коэффициента
поглощения (7) приближенно равно
. Максимальное значение коэффициента
поглощения (7) приближенно равно
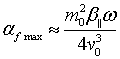 (12)
(12)
В случае ![]() скорость быстрой магнитогидродинамической
волны (6)
скорость быстрой магнитогидродинамической
волны (6)![]() равна скорости гидродинамической волны (8)
в идеальной магнитной жидкости с равновесной намагниченностью при
распространении параллельно магнитному полю [7].
равна скорости гидродинамической волны (8)
в идеальной магнитной жидкости с равновесной намагниченностью при
распространении параллельно магнитному полю [7].
В случае
![]() коэффициент поглощения
коэффициент поглощения
является малой величиной относительно
![]() , т. к.
, т. к. ![]() .
.
В случае ![]() скорость быстрой магнитогидродинамической
волны (6)
скорость быстрой магнитогидродинамической
волны (6) ![]() равна скорости быстрой магнитозвуковой волны
(9) в идеальной магнитной жидкости с вмороженной намагниченностью при
распространении параллельно магнитному полю [4].
равна скорости быстрой магнитозвуковой волны
(9) в идеальной магнитной жидкости с вмороженной намагниченностью при
распространении параллельно магнитному полю [4].
В случае ![]() коэффициент поглощения
коэффициент поглощения
также является малой
величиной относительно ![]() , т. к.
, т. к. ![]() .
.
В частном случае, при распространении волны параллельно магнитному полю коэффициент поглощения быстрой магнитозвуковой волны, который был получен по теории возмущений для магнитной жидкости с вмороженной намагниченностью [12], тождествен формуле (14).
Приравнивая к нулю второй
сомножитель получаем два одинаковых дисперсионных уравнения: одно определяет волну
альфвеновского типа с распространением возмущений ![]() и
и ![]() , а другое - волну альфвеновского типа -
, а другое - волну альфвеновского типа - ![]() и
и ![]() . Решениями
дисперсионных уравнений являются выражения для величины фазовой скорости
. Решениями
дисперсионных уравнений являются выражения для величины фазовой скорости ![]() и коэффициента поглощения волны
альфвеновского типа
и коэффициента поглощения волны
альфвеновского типа
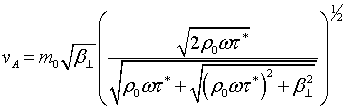 (15)
(15)
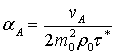 (16)
(16)
В случае
![]() волна альфвеновского типа (15) не
распространяется:
волна альфвеновского типа (15) не
распространяется: ![]() и коэффициент поглощения (16) равен
волновому числу
и коэффициент поглощения (16) равен
волновому числу ![]() , т. е. имеем апериодическое
затухание. В случае
, т. е. имеем апериодическое
затухание. В случае ![]() получается, что
получается, что ![]() , а скорость
, а скорость ![]() стремится
к скорости волны альфвеновского типа в идеальной магнитной жидкости с
вмороженной намагниченностью [4], где
стремится
к скорости волны альфвеновского типа в идеальной магнитной жидкости с
вмороженной намагниченностью [4], где ![]() .
Показательно, что в случае
.
Показательно, что в случае ![]() коэффициент поглощения
коэффициент поглощения
![]() , а в случае
, а в случае ![]() получается,
что
получается,
что ![]() . Значит, при малых
. Значит, при малых ![]() коэффициент поглощения гораздо больше,
чем при больших
коэффициент поглощения гораздо больше,
чем при больших ![]() . В случае
. В случае ![]() коэффициент поглощения существенно меньше
волнового числа
коэффициент поглощения существенно меньше
волнового числа ![]() , поэтому теоретически возможно
распространение волны альфвеновского типа.
, поэтому теоретически возможно
распространение волны альфвеновского типа.
3. Теоретический анализ экспериментальных данных
В работе [3] использовались магнитные
жидкости на основе воды W-40 и
на основе керосина HC-50, которые
производятся компанией Taiho Industies Co., Ltd. У магнитной жидкости W-40 массовая концентрация частиц магнетита ![]() , намагниченность насыщения
, намагниченность насыщения ![]() Гс и плотность
Гс и плотность ![]() г/см3.
Образец магнитной жидкости помещался в измерительную ячейку, которая находилась
в однородном постоянном магнитном поле электромагнита [3]. Расстояние между
пьезопреобразователями ячейки составляло 32 мм. Ячейка находилась в термостате
при температуре
г/см3.
Образец магнитной жидкости помещался в измерительную ячейку, которая находилась
в однородном постоянном магнитном поле электромагнита [3]. Расстояние между
пьезопреобразователями ячейки составляло 32 мм. Ячейка находилась в термостате
при температуре ![]() C. Экспериментальные результаты [3] представлены графическими
зависимостями относительного изменения скорости ультразвука
C. Экспериментальные результаты [3] представлены графическими
зависимостями относительного изменения скорости ультразвука
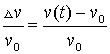 ,
(17)
,
(17)
от времени ![]() воздействия намагничивающего поля. В
соотношении (16) через
воздействия намагничивающего поля. В
соотношении (16) через ![]() обозначена скорость ультразвука в магнитной жидкости
при отсутствии внешнего магнитного поля. В данной серии экспериментов изучалось
распространение ультразвука параллельно магнитному полю
обозначена скорость ультразвука в магнитной жидкости
при отсутствии внешнего магнитного поля. В данной серии экспериментов изучалось
распространение ультразвука параллельно магнитному полю ![]() рис. 1 [3].
рис. 1 [3].
Магнитная жидкость считается магнитной
наножидкостью, когда средний размер магнитных частиц находится в области
нанометровых длин (~5-20 нм) [4]. Для магнитных наночастиц применимо
однодоменное приближение, поэтому магнитная наножидкость эквивалентна
суперперамагнитному газу [4]. Магнитная жидкость находилась в состоянии
термодинамического равновесия, поэтому величину намагниченности магнитной
жидкости в зависимости от величины индукции внешнего поля ![]() оцениваем при помощи формулы Ланжевена [13]
оцениваем при помощи формулы Ланжевена [13]
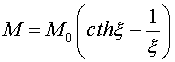 ,
,
где ![]() ,
, ![]() Гс - намагниченность насыщения
магнетита,
Гс - намагниченность насыщения
магнетита, ![]() - намагниченность насыщения соответствующей
магнитной жидкости,
- намагниченность насыщения соответствующей
магнитной жидкости, ![]() - объем частицы магнетита
диаметром
- объем частицы магнетита
диаметром ![]() ,
, ![]() -
константа Больцмана,
-
константа Больцмана, ![]() - температура. Средний диаметр
частиц магнетита для обеих магнитных жидкостей равен 10 нм [3].
- температура. Средний диаметр
частиц магнетита для обеих магнитных жидкостей равен 10 нм [3].
Скорость распространения ультразвука
определяется формулой скорости для быстрой магнитозвуковой волны (6). Для
расчета скорости по уравнениям (6,8-11) значение удельной намагниченности
вычислялось как ![]() . Для значения индукции внешнего магнитного поля
. Для значения индукции внешнего магнитного поля ![]() мТ величина намагниченности равна
мТ величина намагниченности равна ![]() Гс. Поскольку в работе [3] не было
приведено значение скорости ультразвука в отсутствие внешнего магнитного поля,
то для W-40 она предполагалась равной
Гс. Поскольку в работе [3] не было
приведено значение скорости ультразвука в отсутствие внешнего магнитного поля,
то для W-40 она предполагалась равной ![]() см/с, а для HC-50 -
см/с, а для HC-50 - ![]() см/с.
см/с.
Для магнитной жидкости HC-50 массовая концентрация частиц
магнетита ![]() , намагниченность насыщения
, намагниченность насыщения ![]() Гс и плотность
Гс и плотность ![]() г/см3
[3]. Поэтому намагниченность равна
г/см3
[3]. Поэтому намагниченность равна ![]() Гс для значения
индукции внешнего магнитного поля
Гс для значения
индукции внешнего магнитного поля ![]() мТ.
мТ.
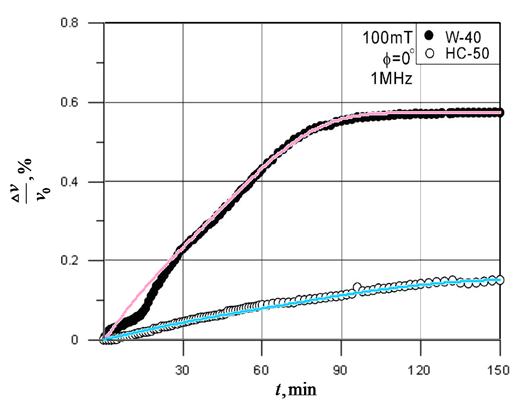
Рис. 1. Зависимость относительного изменения скорости распространения ультразвука параллельно магнитному полю от времени. Кружки – экспериментальные данные [3]. Сплошные кривые – аппроксимация по формулам (18-19).
На рис. 1 оба
экспериментальных графика от ![]() мин до определенного
момента времени с хорошей точностью линейно возрастают, а потом выходят на
постоянную величину. Поэтому на рис. 1 данные графики аппроксимированы гладкими
кривыми: для W-40
мин до определенного
момента времени с хорошей точностью линейно возрастают, а потом выходят на
постоянную величину. Поэтому на рис. 1 данные графики аппроксимированы гладкими
кривыми: для W-40
где 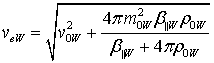 ,
, ![]() ,
, ![]() г/см3,
г/см3,
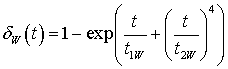 ,
, ![]() мин,
мин, ![]() мин
мин
для HC-50
![]() (19)
(19)
где 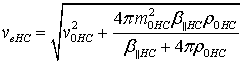 ,
, ![]() ,
,
![]() г/см3,
г/см3,
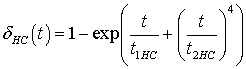 ,
,
![]() мин,
мин, ![]() мин.
мин.
Впервые в работах [5,14]
было показано, что динамические процессы в магнитных жидкостях можно
рассматривать в двух предельных случаях: при временах релаксации ![]() и
и ![]() . В
системе уравнений (1) время
. В
системе уравнений (1) время ![]() является параметром,
который может принимать значения от нуля до бесконечности. Принято считать, что
случай с вмороженной намагниченностью (
является параметром,
который может принимать значения от нуля до бесконечности. Принято считать, что
случай с вмороженной намагниченностью (![]() ) наблюдается
после длительного воздействия однородного постоянного магнитного поля [4]. Это
близко ко времени
) наблюдается
после длительного воздействия однородного постоянного магнитного поля [4]. Это
близко ко времени ![]() мин на рис. 1., и для асимптот
кривых верно
мин на рис. 1., и для асимптот
кривых верно ![]() и
и ![]() .
Можно считать, что случай с равновесной намагниченностью (
.
Можно считать, что случай с равновесной намагниченностью (![]() ) характерен около
) характерен около ![]() мин.
Когда появилось магнитное поле, то изменение скорости ультразвука было очень
малым. В [7] показано, что изменение скорости ультразвука в случае с
равновесной намагниченностью на несколько порядков меньше, чем в случае с вмороженной
намагниченностью. Аппроксимационные значения при
мин.
Когда появилось магнитное поле, то изменение скорости ультразвука было очень
малым. В [7] показано, что изменение скорости ультразвука в случае с
равновесной намагниченностью на несколько порядков меньше, чем в случае с вмороженной
намагниченностью. Аппроксимационные значения при ![]() мин равны
скорости ультразвука в случае с равновесной намагниченностью
мин равны
скорости ультразвука в случае с равновесной намагниченностью ![]() и
и ![]() .
После нескольких часов воздействия однородного постоянного магнитного поля изменение
скорости ультразвука достигла значений, которые описываются моделью магнитной
жидкости с вмороженной намагниченностью. К настоящему времени не создана
микроскопическая теория кинетики установления вмороженной намагниченности [4],
поэтому следует применять феноменологические методы. Вполне логично, что для
моделирования достижения бесконечного значения параметра
.
После нескольких часов воздействия однородного постоянного магнитного поля изменение
скорости ультразвука достигла значений, которые описываются моделью магнитной
жидкости с вмороженной намагниченностью. К настоящему времени не создана
микроскопическая теория кинетики установления вмороженной намагниченности [4],
поэтому следует применять феноменологические методы. Вполне логично, что для
моделирования достижения бесконечного значения параметра ![]() за конечные отрезки времени была
применена экспоненциальная зависимость (18-19).
за конечные отрезки времени была
применена экспоненциальная зависимость (18-19).
Время
релаксации ![]() выражено из (6,8-11)
выражено из (6,8-11)
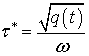 (20)
(20)
где
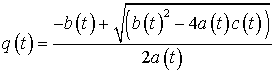 ,
,
![]() ,
,
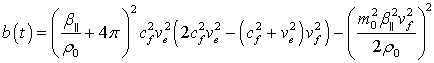 ,
,
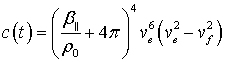 .
.
В (20) ![]() приравниваем
приравниваем ![]() и
и ![]() , и получаем
, и получаем ![]() ,
соответственно, для двух магнитных жидкостей. Далее, используем эти
,
соответственно, для двух магнитных жидкостей. Далее, используем эти ![]() при вычислении коэффициентов поглощения
ультразвука
при вычислении коэффициентов поглощения
ультразвука ![]() для W-40 и HC-50
по формулам (6-11). Дискриминант в (20) положителен, т. к.
для W-40 и HC-50
по формулам (6-11). Дискриминант в (20) положителен, т. к. ![]() и
и ![]() .
Функция
.
Функция ![]() изменяет знак:
изменяет знак: ![]() и
и
![]() . Функция
. Функция ![]() и,
далее,
и,
далее, ![]() . Расчетные кривые изображены на рис. 2. Из
(6-11,13) следует, что значения обоих коэффициентов поглощения и
. Расчетные кривые изображены на рис. 2. Из
(6-11,13) следует, что значения обоих коэффициентов поглощения и ![]() равны нулю с математической строгостью
при
равны нулю с математической строгостью
при ![]() . Это подтверждено с хорошей точностью при
помощи вычислительных программ.
. Это подтверждено с хорошей точностью при
помощи вычислительных программ.
Для двух магнитных
наножидкостей с различными основами подошла аппроксимация с одинаковой
аналитической зависимостью (18-19). Возможен еще вариант обработки
экспериментальных данных рис.1 [3]: можно сделать вычисление ![]() и коэффициентов поглощения
и коэффициентов поглощения ![]() и
и ![]() по
экспериментальным точкам. Однако, в данном методе возникает неоднозначность с
определением асимптоты при
по
экспериментальным точкам. Однако, в данном методе возникает неоднозначность с
определением асимптоты при ![]() для вычисления
для вычисления ![]() и
и ![]() .
.
Для W-40 на интервале ![]() мин получилось
максимальное расчетное значение
мин получилось
максимальное расчетное значение ![]() см-1 рис. 2
меньше, чем
см-1 рис. 2
меньше, чем ![]() см-1 в экспериментальных
данных для похожей магнитной жидкости на основе воды в магнитном поле с
индукцией
см-1 в экспериментальных
данных для похожей магнитной жидкости на основе воды в магнитном поле с
индукцией ![]() мТ и при частоте ультразвука
мТ и при частоте ультразвука ![]() Гц [15]. В [15] использовалась магнитная
жидкость с меньшей концентрацией магнитных частиц, поэтому коэффициент
поглощения для W-40 может быть
немного больше в экспериментах. Приближенное значение коэффициента поглощения
по формуле (13) равно
Гц [15]. В [15] использовалась магнитная
жидкость с меньшей концентрацией магнитных частиц, поэтому коэффициент
поглощения для W-40 может быть
немного больше в экспериментах. Приближенное значение коэффициента поглощения
по формуле (13) равно ![]() см-1, что близко со
значением на рис. 2.
см-1, что близко со
значением на рис. 2.
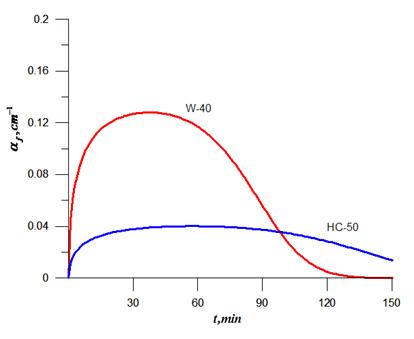
Рис. 2. Зависимость коэффициентов
поглощения ультразвука в магнитных жидкостях W-40 и HC-50
от времени воздействия магнитного поля с индукцией ![]() мТ по
формулам (6-11,20).
мТ по
формулам (6-11,20).
Коэффициент поглощения
ультразвука складывается из действия механизмов теплопроводности, вязкости и
релаксации магнитного поля к своему равновесному значению. При учете механизма
релаксации максимальное расчетное значение оказалось не гораздо меньше, а сравнимо
![]() см-1 с экспериментальным (
см-1 с экспериментальным (![]() см-1 и
см-1 и ![]() см-1).
После
см-1).
После ![]() мин расчетный коэффициент поглощения для W-40 равен
мин расчетный коэффициент поглощения для W-40 равен ![]() см-1,
что практически незаметно на фоне экспериментального
см-1,
что практически незаметно на фоне экспериментального ![]() см-1 и максимального
расчетного значения
см-1 и максимального
расчетного значения ![]() см-1. Значит,
механизм релаксации действует на поглощение ультразвука в течение
приблизительно двух часов. При установлении вмороженной намагниченности
время релаксации
см-1. Значит,
механизм релаксации действует на поглощение ультразвука в течение
приблизительно двух часов. При установлении вмороженной намагниченности
время релаксации ![]() стремится к бесконечности, и,
поэтому, коэффициент поглощения стремится к нулю. Это согласуется с
результатом, который получен по теории возмущений (14) [12].
стремится к бесконечности, и,
поэтому, коэффициент поглощения стремится к нулю. Это согласуется с
результатом, который получен по теории возмущений (14) [12].
Для HC-50 на интервале ![]() мин максимальное расчетное значение
мин максимальное расчетное значение ![]() см-1 на рис. 2 получилось меньше,
чем максимальное для W-40. Приближенное
значение коэффициента поглощения по формуле (13) равно
см-1 на рис. 2 получилось меньше,
чем максимальное для W-40. Приближенное
значение коэффициента поглощения по формуле (13) равно ![]() см-1,
что близко со значением на рис. 2. После
см-1,
что близко со значением на рис. 2. После ![]() мин расчетный
коэффициент поглощения для HC-50
равен
мин расчетный
коэффициент поглощения для HC-50
равен ![]() см-1, что больше, чем для W-40. Значит, вмороженная
намагниченность устанавливается медленнее, приблизительно за три часа
воздействия однородного стационарного магнитного поля. Это может зависеть от
свойств жидкости-основы. В магнитные жидкости добавляют поверхностно-активное
вещество, которое образует слои на поверхности магнитных наночастиц. Это препятствует
слипанию наночастиц при диполь-дипольном взаимодействии. В магнитной жидкости
на основе керосина наночастицы покрываются одним слоем поверхностно-активного
вещества, а на основе воды – двумя слоями [4]. Из таких наночастиц образуются
цепевидные кластеры в постоянном магнитном поле. В магнитной жидкости на основе
керосина данные кластеры получаются меньшего размера, чем в магнитной жидкости на
основе воды.
см-1, что больше, чем для W-40. Значит, вмороженная
намагниченность устанавливается медленнее, приблизительно за три часа
воздействия однородного стационарного магнитного поля. Это может зависеть от
свойств жидкости-основы. В магнитные жидкости добавляют поверхностно-активное
вещество, которое образует слои на поверхности магнитных наночастиц. Это препятствует
слипанию наночастиц при диполь-дипольном взаимодействии. В магнитной жидкости
на основе керосина наночастицы покрываются одним слоем поверхностно-активного
вещества, а на основе воды – двумя слоями [4]. Из таких наночастиц образуются
цепевидные кластеры в постоянном магнитном поле. В магнитной жидкости на основе
керосина данные кластеры получаются меньшего размера, чем в магнитной жидкости на
основе воды.
4. Выводы
Из многих источников следует, что магнитная жидкость с вмороженной намагниченностью образуется после десятков или сотен часов воздействия однородного постоянного магнитного поля [4]. На основании системы уравнений работ [8,9] получены скорости распространения и коэффициенты поглощения ультразвука в магнитных жидкостях при учете процесса релаксации магнитного поля к своему равновесному значению. Из теоретического анализа экспериментальных данных [3] по изменению скорости ультразвука в магнитных наножидкостях на основе воды и керосина следует, что расчетные коэффициенты поглощения ультразвука заметны на фоне наблюдаемых в течение приблизительно двух часов, а потом практически стремятся к нулю при длительном воздействии однородного постоянного магнитного поля. Это означает, что при установившейся вмороженной намагниченности механизм релаксации магнитного поля практически не дает вклада в коэффициент поглощения ультразвука. Согласно полученным результатам, после длительного воздействия однородного постоянного магнитного поля, поглощение ультразвука определяется в основном вязкостью и теплопроводностью магнитной жидкости.
Литература
[1] Y. Takeda, “Velocity Profile Measurement by Ultrasonic Doppler Shift Method”, // Int. J. Heat Fluid Flow 1986. Vol. 7. No. 4. p. 313-318.
[2] H. Kikura, Y. Takeda and F. Durst, “Velocity Profile Measurement of the Taylor Vortex Flow of a Magnetic Fluid Using the Ultrasonic Doppler Method”, // Exp. Fluids 1999. Vol. 26. No. 3. p. 208-214.
[3] M. Motozawa, Y. Matsumoto and T. Sawada, “Properties of Ultrasonic Propagation in Functional Fluids under Magnetic Fields”, // Int. J. Modern Phys. B 2007. Vol. 21. Nos. 28-29. p. 4914-4921.
[4] V.V. Sokolov, “Wave Propagation in Magnetic Nanofluids (A Reiew)”, // Acoustical Physics. 2010. Vol. 56. No. 6. pp. 972-988. DOI : 10.1134/S1063771010060229
[5] V.V. Sokolov, V.V. Tolmachev, “Employment of Generalized Virtual Work Principle in Ferrohydrodynamics. 2. Magnetic Fluid with Frozen Magnetization”, // Magn. Gidrodin., 1997. vol. 32, No. 3, p. 291-294.
[6] I.E. Ovchinnikov, V.V. Sokolov, “Effect of an External Magnetic Field on the Propagation Velocities of Magnetoacoustic Waves in a Magnetic Fluid”, // Acoustical Physics, 2009. Vol.55, No. 3, p. 359-364. DOI: 10.1134/S106377100903117
[7] I.E. Ovchinnikov, V.V. Sokolov, “Waves in Magnetic Fluids with Equilibrium and Frozen-In Magnetizations”, // Acoustical Physics, 2013. Vol. 59, No. 1, p. 51-55. DOI: 10.1134/S1063771012060115
[8] V.V. Sokolov, V.V. Tolmachev, “Propagation of shear waves in a magnetic liquid with frozen-in magnetization”, // Tech. Phys. Lett. 1997. Vol. 23, No. 1 p. 5-6.
[9] B.U. Felderhof, V.V. Sokolov, P.A. Eminov, “Ferrofluid Dynamics, Magnetic Relaxation and Irreversible Thermodynamics”, // Journal of Chemical Physics. 2010. Vol. 132. No. 18. p. 184907. http://dx.doi.org/10.1063/1.3430726
[10] Landau L.D., Lifshitz E.M. Electrodynamics of Continuous Media. New York: Pergamon, 1984.
[11] R.V. Polovin, V.P. Demutskii, Fundamentals of Magnetohydrodynamics, London, Plenum Publishing, 1990.
[12] В.В. Соколов, И. Э. Овчинников, “Поглощение гидродинамических волн в магнитной жидкости”, // Ежегодный сборник научных трудов. Фундаментальные физико-математические проблемы и моделирование технико-технологических систем, вып. 12, том 1, 2009, М.: Янус-К, с. 162-169. (V.V.Sokolov, I.E. Ovchinnikov, “Hydrodynamic Waves Absorption in Magnetic Fluid”, // Annual Transactions. Fundamental Physico-Mathematical Problems and Modelling Technico-Technological Systems, No. 12, Book 1, 2009, Moscow, Yanus-K, p. 162-169 [in Russian])
[13] V.E. Fertman, Magnetic Fluids Guidebook: Properties and Applications, Hemisphere Publ. Corp., N. Y., 1990.
[14] V.V. Sokolov, V.V. Tolmachev, “Employment of Generalized Virtual Work Principle in Ferrohydrodynamics. 1. Magnetic Fluid with Free Magnetization”, // Magn. Gidrodin., 1997. Vol. 32, No. 3, p. 286-290.
[15] T. Hornowski Ultrasonic Properties of EMG-605 Magnetic Liquid // Proc. of SPIE. 2005. Vol. 5828. p. 205-212. http://dx.doi.org/10.1117/12.612810