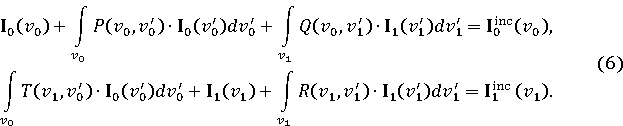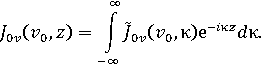РАСЧЁТ ВЗАИМНОЙ СВЯЗИ ДВУХ ПРОДОЛЬНЫХ ЩЕЛЕЙ НА ИДЕАЛЬНО ПРОВОДЯЩЕМ ЦИЛИНДРЕ, РАСПОЛОЖЕННОМ В ДИЭЛЕКТРИЧЕСКОЙ ОБЛАСТИ СЛОЖНОЙ ФОРМЫ *
А. В. Бунин, А. А. Комаров
Национальный исследовательский университет «МЭИ»,
кафедра Антенных устройств и распространения радиоволн
Получена 20 января 2013 г.
Аннотация. Задача сводится к системе трёх поверхностных интегральных уравнений (ПИУ) относительно электрического тока на поверхности металла и эквивалентных токов на внешней поверхности диэлектрика. Система уравнений решается численно. По вычисленному распределению электрического тока на поверхности металла рассчитывается коэффициент взаимной связи двух щелей. Проводится сравнение с результатами, полученными другими методами.
Ключевые слова: взаимная связь, продольные щели на идеально проводящем цилиндре, метод поверхностных интегральных уравнений, преобразование Фурье.
Abstract: The problem is reduced to a system of integral equations relative to an electric current on the metal surface and equivalent currents on the outer dielectric surface. System of equations is numerically solved. Coupling between two slots is calculated over the numerical distributions of the electric current on the metal surface. Comparison with other methods data is demonstrated.
Key words: coupling, axial slots in conducting cylinders, surface integral equations method, Fourier transform.
Введение
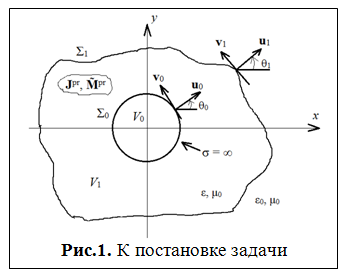
Постановка задачи представлена на рис. 1. Идеально проводящий круговой
цилиндр расположен в диэлектрической области сложной формы. Диэлектрическая
область V1 с произвольной комплексной
диэлектрической проницаемостью ограничена двумя поверхностями. Внутренняя
поверхность диэлектрика Σ0 совпадает с поверхностью цилиндра. Внешняя
поверхность диэлектрика обозначена Σ1. Параметры
внешней по отношению к диэлектрику области характеризуются величинами ε = 1, μ = 1 (свободное пространство). Первичные источники Jpr, 
расположены внутри диэлектрической области.
В работе [1] методом поверхностных интегральных уравнений (ПИУ) совместно с использованием преобразования Фурье решена задача о расчёте взаимной проводимости двух продольных щелей на идеально проводящем цилиндре произвольного поперечного сечения. В настоящей работе исследовано влияние внешней диэлектрической области на взаимную связь двух щелевых антенн.
В работе [2] показано, что задача о возбуждении идеально проводящего тела, покрытого слоем диэлектрика, может быть сведена к системе интегральных уравнений относительно эквивалентных поверхностных токов
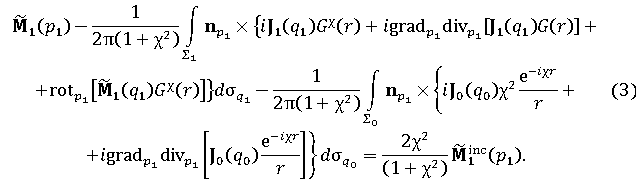
Здесь J0 – поверхностный электрический ток на идеально
проводящем цилиндре; J1 –
эквивалентный электрический ток на внешней поверхности диэлектрика;
– эквивалентный магнитный ток; W0 = 120π Ом; p – точка наблюдения; q – точка интегрирования; r – расстояние между точками
интегрирования и наблюдения; 
– единичный вектор нормали к
поверхности Σi в точке pi; χ
– показатель преломления диэлектрического тела.
Поверхностные плотности эквивалентных электрических и магнитных токов, по определению, равны
Ji = ni×Hi, Mi = – ni×Ei,
где Ei и Hi – полные электрические и магнитные поля на поверхности тела Σi.
Все координаты и расстояния в (1) – (3) умножены на волновое число свободного пространства. Кроме того, введены обозначения
1. Интегральные уравнения в обобщённой цилиндрической системе координат
При численном решении системы ПИУ (1) – (3) используем методику, изложенную в [3]. На каждой из поверхностей Σ0 и Σ1 вводится обобщённая цилиндрическая ортогональная система координат u, v, z (рис.1). Наряду с цилиндрическими координатами в дальнейшем применяются также прямоугольные координаты x, y. Искомые и первичные поверхностные токи, а также обе функции Грина представляем в виде интегралов Фурье по продольной координате z:
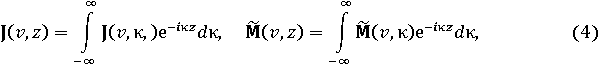
где
После подстановки представлений (4), (5) в исходную систему уравнений можно провести интегрирование по координате z' с учётом ортогональности экспоненциальных функций. В результате для каждого значения спектральной переменной κ получается система из шести одномерных интегральных уравнений, содержащих интегралы по контурам поперечных сечений тел. Эту систему удобно записать в матричной форме:
Здесь I1(υ1)
– вектор плотности эквивалентного тока на поверхности Σ1, характеризуемый четырьмя составляющими:
– вектор
плотности электрического тока на идеально проводящей поверхности цилиндра Σ0, имеющий две компоненты J0υ и J0z.
Матричное ядро R системы уравнений (6) характерно для задачи возбуждения диэлектрического тела [4]. Ядро P соответствует задаче возбуждения идеально проводящего тела. Ядра Q и T, учитывающие взаимодействие токов, текущих по идеально проводящей поверхности и поверхности диэлектрика, могут быть выражены через элементы ядра R.
В нашем случае падающее поле создаётся полем излучения продольной щели. Считаем, что щель возбуждается отрезком прямоугольного волновода с единственной распространяющейся модой H10. Это равносильно тому, что щель возбуждается первичным полем
где Δ – поперечный размер щели; 2l – продольный размер;
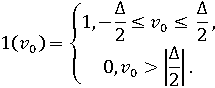
Как известно [5], щель электродинамически эквивалентна поверхностному магнитному току
Для определения правых частей системы уравнений (6) сначала по теореме эквивалентности [6] вычисляются поля, создаваемые поверхностным магнитным током (7). Затем с помощью преобразования Фурье находятся спектральные плотности. В результате имеем следующие выражения для правых частей (6)
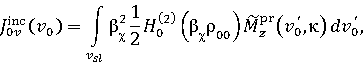
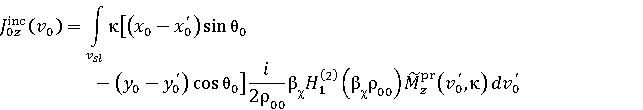
на поверхности Σ0 и
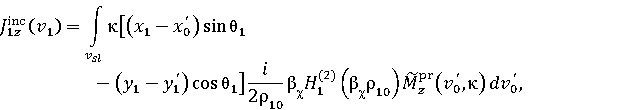
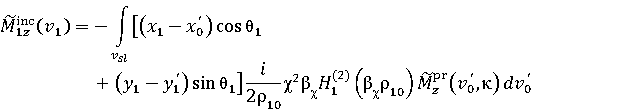
на поверхности Σ1. Здесь введены обозначения
– спектральная плотность магнитного
тока, равная
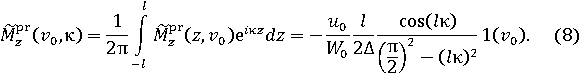
2. Численное решение системы интегральных уравнений
Система интегральных уравнений (6) решается численно с помощью метода Крылова-Боголюбова, в соответствии с которым интервал интегрирования в каждом интеграле системы (6) делится на малые интервалы Δυ, а искомые функции заменяются кусочно-постоянными. В результате этого решение системы интегральных уравнений сводится к решению эквивалентной системы линейных алгебраических уравнений (СЛАУ) вида
где I0 – столбец, составленный из N0 значений искомой плотности тока I0 в серединах интервалов разбиения контура поперечного сечения идеально проводящего цилиндра; I1 – столбец, составленный из N1 значений искомой плотности тока I1 в серединах интервалов разбиения контура поперечного сечения внешней диэлектрической области.
Элементы матриц P̂, Q̂, T̂, R̂ представляют собой интегралы по малым интервалам Δυ от ядер P, Q, T, R соответственно. Порядок матрицы коэффициентов алгебраической системы (9) равен (2N0 + 4N1), а сама матрица имеет следующую структуру
где 
– единичная матрица.
Таким образом, решение задачи сводится к обращению комплексной матрицы (2N0 + 4N1) – го порядка.
В данной работе решается задача возбуждения бесконечных цилиндрических структур сосредоточенным источником, т.е. рассматривается трёхмерная задача. Использование преобразования Фурье позволяет свести исходную трёхмерную задачу к набору независимых двумерных задач, которые намного удобнее для численного решения.
Формально, двумерную задачу (6) необходимо решать для бесконечного набора значений спектральной переменной κ. При численной реализации область изменения пространственной частоты κ ограничивается верхним значением κmax, т.е. вместо исходного интервала |κ| < ∞ имеем |κ| ≤ κmax. Полученный интервал можно уменьшить в два раза, если учесть тот факт, что искомые неизвестные системы (6) являются чётными или нечётными функциями спектральной переменной κ. Это означает, что достаточно решать задачу (6) в диапазоне 0 ≤ κ ≤ κmax. Далее этот интервал дискретизируется с шагом Δκ. Всего имеем Nκ = κmax/Δκ +1 спектральных отсчётов.
Таким образом, при численной реализации СЛАУ (9) отдельно решается для Nκ дискретных значений из интервала κ ≤ κmax.
Возникает естественный вопрос, как выбрать κmax и Δκ. Как известно [7], периодическому сигналу с периодом повторения T соответствует дискретный спектр с расстоянием между соседними гармониками – 2π/T. Применительно к нашему случаю это означает, что при дискретизации непрерывного пространственного спектра щели мы заменяем исходную задачу возбуждения цилиндрических структур щелью на задачу возбуждения тех же структур периодической щелевой решёткой. Если пространственный период фиктивной щелевой решётки равен Zarray, то шаг дискретизации – Δκ = 2π/Zarray.
Период решётки выбираем из условия, что взаимная связь фиктивных щелей с приёмной щелью гораздо меньше, чем связь между передающей и приёмной щелями. Граничное значение κmax будем определять из численного эксперимента, сравнивая сходимость величины взаимной связи при разных значениях κmax.
При численном решении системы (6) возникает ещё одна проблема [1]. Оказывается, что на некоторых спектральных частотах происходит потеря точности решения СЛАУ (9).
Связано это со следующим фактом. Однородная система (6) соответствует задаче нахождения собственных волн рассматриваемой структуры (рис.1). Постоянные распространения определяются из условия равенства нулю определителя СЛАУ (9). Таким образом, если при численном решении неоднородной системы (6) мы попадаем на резонансное значение κ, то произойдёт катастрофическая потеря точности за счёт резкого уменьшения величины определителя СЛАУ.
В нашем случае возможны резонансы двух типов: резонанс области V0, внутренней по отношению к поверхности Σ0, и резонанс области V1, заключённой между поверхностями Σ0 и Σ1 (диэлектрический волновод).
Для борьбы с резонансом в области V0 применяется следующее условие [8]: полное поле Hz приравнивается нулю в одной или нескольких точках области V0, что исключает собственные волны. Если резонанс отсутствует, то поле в области V0 равно нулю и без дополнительных условий. Когда резонанс есть, это условие исключает собственные волны, уничтожая тем самым причину потери точности.
Резонанс в области V1 соответствует наличию распространяющихся волн в диэлектрическом волноводе. Самый простой способ исключения собственных волн – это введение потерь. В этом случае диэлектрическая проницаемость и постоянная распространения будут комплексными величинами, что приведёт к затуханию распространяющихся волн.
3. Расчёт коэффициентов отражения и передачи
После решения системы уравнений (6) нам известна спектральная плотность поверхностного тока J0υ(υ0,κ) наведённого на поверхности цилиндра в результате взаимодействия с внешней областью. Поверхностный ток вычисляется по формуле обратного преобразования Фурье
Собственная проводимость щели рассчитывается по формуле
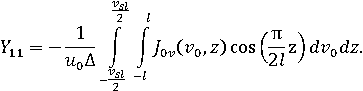
С учетом выражения поверхностного тока через спектральную плотность удаётся провести интегрирование по z, что приводит к окончательному выражению
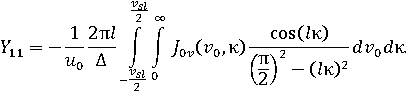
Аналогичным образом получаем выражение для взаимной проводимости щелей
Элементы матрицы рассеяния S11 и S21 рассчитываются по известным соотношениям [9]:
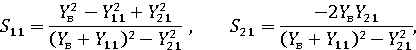
где YВ – проводимость волновода, питающего щель.
4. Результаты расчётов
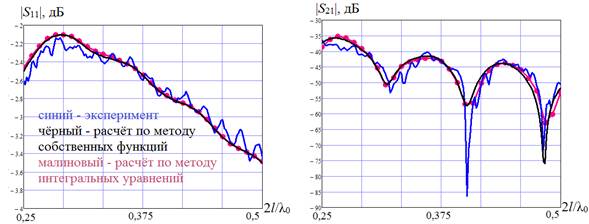
Работоспособность и точность развитого расчётного аппарата проверялась сравнением его результатов с расчётными данными, полученными другим методом и результатами измерений.
По изложенной методике был проведён расчёт коэффициентов отражения и связи двух продольных щелей в диапазоне частот при погружении идеально проводящего цилиндра в соосный диэлектрический цилиндр (рис.2).
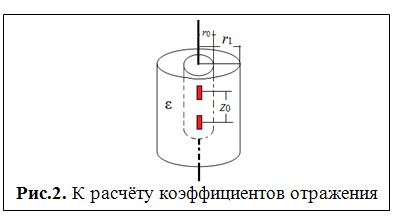
Радиус металлического цилиндра – l; радиус соосного диэлектрического цилиндра – 20l. Размеры щелей – 2l на l/3. Щели расположены на расстоянии 4l друг от друга на одной оси. Диэлектрическая проницаемость материала равна ε = 2,55 – i0,2.
Для этой же задачи были проведены расчёты методом собственных функций (СФ) [10].
Для экспериментальной проверки были изготовлены широкополосные щелевые антенны. Диэлектрическая проницаемость и тангенс угла диэлектрических потерь диэлектрической оболочки измерялась с точностью не хуже ± 5%. Для измерений S11 и S21 использовался векторный анализатор цепей типа Agilent N5230A.
Сравнение расчетов с результатами экспериментов, представленное на рис.3, показывает, что результаты, полученные методами ПИУ и СФ, весьма близки и согласуются с данными измерений. Небольшие колебания результатов измерений с изменением длины волны обусловлены отражениями поля, связанными с конечными размерами цилиндра и ящика, в который он был помещен.
|
Рис.3. Зависимость коэффициентов отражения и передачи |
Следует отметить, что разработанная методика расчета взаимной связи щелей обобщается на случай наклонного расположения щелей, а также на случай, когда щелевые антенны расположены на цилиндре произвольного поперечного сечения.
В заключение авторы считают своим приятным долгом выразить признательность профессорам В.В. Бодрову и В.А. Пермякову за полезные обсуждения.
1. A.F. Peterson and R. Mittra, “Mutual admittance between slots in cylinders of arbitrary shape,” IEEE Trans. Antennas Propagat., vol. 37, pp. 858 – 864, July 1989.
2. Васильев Е.Н., Материкова Л.В. Возбуждение идеально проводящего тела, покрытого слоем диэлектрика, Известия ВУЗов – Радиофизика, т. 14, № 8, 1250 – 1259, (1971)
3. Васильев Е.Н., Солодухов В.В. Метод интегральных уравнений в задачах дифракции на полубесконечных диэлектрических структурах. Препринт № 25(397), -М.: ИРЭ АН СССР, 1984. – 45 с.
4. Васильев Е.Н., Солодухов В.В. Дифракция плоской электромагнитной волны на диэлектрическом цилиндре с произвольной формой поперечного сечения, Журнал Технической Физики, т. 40, № 1, 47 – 53, (1970)
5. Марков Г.Т., Петров Б.М., Грудинская Г.П. Электродинамика и распространение радиоволн. – М.: Сов. Радио, 1979. – 374 с.
6. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. – М.: Радио и связь, 1983. – 296 с.
7. Баскаков С.И. Радиотехнические цепи и сигналы: Учеб. для вузов. по спец. «Радиотехника». – М.: Высш. шк., 2000.
8. Васильев Е.Н. Возбуждение тел вращения. – М.: Радио и связь, 1987. – 272 с., ил.
9. Сазонов Д.М. Антенны и устройства СВЧ. – М.: Высш. шк., 1988. – 432 с.
10. Бунин А.В., Фролов П.А. Излучение щелевых антенн на цилиндрических телах, покрытых слоем ионизированного газа, Оптимизация антенн, СВЧ устройств и радиолиний. – Тр. Моск.энерг.ин-т, вып. 610, 57 – 61, (1983).