УДК 621.396, 621.317.7
АЛГОРИТМ ОЦЕНКИ ЧАСТОТНЫХ СВОЙСТВ ОТДЕЛЬНЫХ ОТРАЖАТЕЛЕЙ ПРИ НЕДОСТАТОЧНОМ РАЗРЕШЕНИИ ВО ВРЕМЕННОЙ ОБЛАСТИ *
А. А. Савин
Томский государственный университет систем управления и радиоэлектроники
Получена 20 декабря 2012 г.
Аннотация. В работе решена задача синтеза фильтра, реализующего квазиоптимальные оценки частотных характеристик двух или более близкорасположенных отражателей, локализованных во временной области. Алгоритм реализован в предположении гауссовой модели канала с независимыми рассеивателями при обработке частотной характеристики канала. Способ обработки измерений основан на применении квазиоптимального фильтра, использующего UT (the unscented transformation) преобразование. Показаны сходимость оценок и работоспособность алгоритма обработки. Методом математического моделирования получены статистические характеристики точности оценок частотных характеристики отдельных отражателей. Приведены результаты обработки экспериментальных данных, полученных при помощи векторного анализатора цепей. В качестве объекта исследования выбран верификационный стандарт Битти. Измерения комплексного коэффициента отражения стандарта выполнены в диапазоне частот от 10 МГц до 18 ГГц.
Ключевые слова: импульсная характеристика, частотная характеристика, алгоритм фильтрации, стандарт Битти.
Введение
Наиболее простой
моделью объекта, отражающего падающую на него электромагнитную волну, является
модель в виде совокупности «блестящих» точек. Отраженный сигнал при
использовании такой модели можно представить как результат вторичного излучения
нескольких независимых рассеивателей [1]. Разрешение двух близкорасположенных
точечных отражателей по дальности возможно только при достаточно высокой
разрешающей способности, которая определяется полосой зондирующего сигнала. В
современных системах импульсную характеристику (ИХ) канала отражения или
передачи ![]() можно оценить с высокой точностью при
помощи широкополосного или импульсного воздействия [2]. Отклик от распределенной
цели, находящейся на некотором расстоянии от передающего и приемного пунктов,
приводит к появлению существенных значений отсчетов ИХ в каждом элементе
разрешения по дальности в окрестности основной дальности до цели.
можно оценить с высокой точностью при
помощи широкополосного или импульсного воздействия [2]. Отклик от распределенной
цели, находящейся на некотором расстоянии от передающего и приемного пунктов,
приводит к появлению существенных значений отсчетов ИХ в каждом элементе
разрешения по дальности в окрестности основной дальности до цели.
Однако в пределах
некоторого ![]() -го элемента разрешения по дальности может
оказаться несколько действующих «блестящих» точек. В этом случае возникает
частотная зависимость свойств отражателя, соответствующего данному элементу
разрешения. При этом оказывается не достаточным знать задержку
-го элемента разрешения по дальности может
оказаться несколько действующих «блестящих» точек. В этом случае возникает
частотная зависимость свойств отражателя, соответствующего данному элементу
разрешения. При этом оказывается не достаточным знать задержку ![]() , постоянные амплитуду
, постоянные амплитуду ![]() и фазу
и фазу ![]() . Причинами
частотной зависимости параметров рассеивателей могут быть и другие факторы.
. Причинами
частотной зависимости параметров рассеивателей могут быть и другие факторы.
Для нахождения
частотных свойств интересующего отражателя можно использовать процедуру
фильтрации пика ИХ во временной области (выделение с помощью некоторой оконной
функции ![]() ) и последующим расчетом частотной
характеристики (ЧХ) при помощи преобразования Фурье (ПФ):
) и последующим расчетом частотной
характеристики (ЧХ) при помощи преобразования Фурье (ПФ): ![]() , где
, где ![]() – оператор прямого
преобразования Фурье. Если интерес представляют свойства отражателей, которые
расположены в соседних или близких элементах разрешения, то методы фильтрации
во временной области становятся не эффективными. Это обусловлено тем, что
точность выделения существенно снижается за счет влияния соседних отражателей
или уменьшения ширины оконной функции.
– оператор прямого
преобразования Фурье. Если интерес представляют свойства отражателей, которые
расположены в соседних или близких элементах разрешения, то методы фильтрации
во временной области становятся не эффективными. Это обусловлено тем, что
точность выделения существенно снижается за счет влияния соседних отражателей
или уменьшения ширины оконной функции.
2. Синтез алгоритма фильтрации
Синтез алгоритма оценки частотных характеристик двух или более близких по задержкам отражателей выполним методами марковской теории нелинейной фильтрации [3] с использованием численного алгоритма UT преобразования (the unscented transformation) [4].
Допустим, что имеется
фрагмент из ![]() отсчетов ИХ, содержащий отклики от
отсчетов ИХ, содержащий отклики от ![]() близкорасположенных отражателей. Значения
их задержек
близкорасположенных отражателей. Значения
их задержек ![]() известны и соответствуют номерам
известны и соответствуют номерам ![]() конкретных элементов разрешения по
дальности, в которых размещаются отражатели. Очевидно, что
конкретных элементов разрешения по
дальности, в которых размещаются отражатели. Очевидно, что ![]() отсчетам ИХ соответствуют
отсчетам ИХ соответствуют ![]() отсчетов ЧХ рассматриваемого группового
объекта. Частотные свойства каждого отражателя опишем набором из
отсчетов ЧХ рассматриваемого группового
объекта. Частотные свойства каждого отражателя опишем набором из ![]() комплексных величин
комплексных величин ![]() , где
, где ![]() . При
выборе
. При
выборе ![]() из условия
из условия ![]() для
получения свойств отражателей на некоторых частотах потребуется интерполяция.
Можно полагать, что ЧХ отражателя, локализованного на временной оси, является
достаточно медленной функцией частоты. Предложенная частотно-временная модель
канала распространения радиоволн содержит
для
получения свойств отражателей на некоторых частотах потребуется интерполяция.
Можно полагать, что ЧХ отражателя, локализованного на временной оси, является
достаточно медленной функцией частоты. Предложенная частотно-временная модель
канала распространения радиоволн содержит ![]() точек
и схематично изображена на рис. 1.
точек
и схематично изображена на рис. 1.

Рис. 1. Частотно-временная модель канала
Выражение для расчета ЧХ через параметры рассмотренной модели имеет вид:
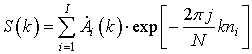 , (1)
, (1)
где ![]() –
номер отражателя;
–
номер отражателя; ![]() – интерполированное значение
комплексной амплитуды
– интерполированное значение
комплексной амплитуды ![]() -го отражателя на относительную
частоту
-го отражателя на относительную
частоту ![]() . Интерполяция производится при помощи
набора
. Интерполяция производится при помощи
набора ![]() . Формула (1) отличается от алгоритма
дискретного ПФ тем, что суммирование производится по
. Формула (1) отличается от алгоритма
дискретного ПФ тем, что суммирование производится по ![]() отсчетам
вместо
отсчетам
вместо ![]() , а также наличием частотно-зависимой
амплитуды.
, а также наличием частотно-зависимой
амплитуды.
Введем ![]() -мерный вектор переменных состояния
-мерный вектор переменных состояния
![]() .
(2)
.
(2)
Для любого типа интерполяции ЧХ по
значениям ![]() координаты в (2) постоянны при изменении
текущей частоты и являются неизвестными случайными величинами. Очевидно, что
при дискретном изменении частоты для вектора
координаты в (2) постоянны при изменении
текущей частоты и являются неизвестными случайными величинами. Очевидно, что
при дискретном изменении частоты для вектора ![]() справедлива
система разностных уравнений
справедлива
система разностных уравнений
![]() .
(3)
.
(3)
Полагаем далее, что для (2) случайные
начальные условия определены заданием априорной плотности распределения
вероятностей (ПРВ) с нулевым средним значением ![]() и
известной ковариационной матрицей
и
известной ковариационной матрицей ![]() .
.
При последовательной
обработке ЧХ канала (то есть для ![]() ), наблюдаемый
комплексный сигнал можно представить в виде
), наблюдаемый
комплексный сигнал можно представить в виде
![]() .
(4)
.
(4)
Полагаем, что погрешность ![]() имеет гауссову ПРВ с нулевым средним
значением и известной дисперсией
имеет гауссову ПРВ с нулевым средним
значением и известной дисперсией ![]() . Модель системы (2) и
(4) также можно записать через квадратуры. Погрешности измерения квадратур ЧХ
являются независимыми случайными величинами и обусловлены несколькими
факторами: формой и спектром зондирующего сигнала (одного или нескольких),
способом обработки и получения значения ЧХ на определенной частоте, уровнем
шумов и пр. Также следует отметить, что сигнал
. Модель системы (2) и
(4) также можно записать через квадратуры. Погрешности измерения квадратур ЧХ
являются независимыми случайными величинами и обусловлены несколькими
факторами: формой и спектром зондирующего сигнала (одного или нескольких),
способом обработки и получения значения ЧХ на определенной частоте, уровнем
шумов и пр. Также следует отметить, что сигнал ![]() в
общем случае нелинейно связан с вектором
в
общем случае нелинейно связан с вектором ![]() .
Характер нелинейности определяется способом интерполяции ЧХ. В работе
использована интерполяция кубическими сплайнами.
.
Характер нелинейности определяется способом интерполяции ЧХ. В работе
использована интерполяция кубическими сплайнами.
Задача байесовой оценки
состояний динамической системы в постановке марковской теории нелинейной
фильтрации [3] при заданной функции потерь определена заданием линейных
уравнений (3) и нелинейного уравнения (4). Для квадратичной функции потерь
оптимальная оценка ![]() текущего состояния
текущего состояния ![]() реализуется в виде оператора
апостериорного среднего при полученной последовательности наблюдений. В силу
нелинейности уравнения (4) апостериорная ПРВ в данной задаче не является
гауссовой. Оператор апостериорного среднего не может быть строго представлен в
замкнутой форме в виде рекуррентных соотношений для оценки
реализуется в виде оператора
апостериорного среднего при полученной последовательности наблюдений. В силу
нелинейности уравнения (4) апостериорная ПРВ в данной задаче не является
гауссовой. Оператор апостериорного среднего не может быть строго представлен в
замкнутой форме в виде рекуррентных соотношений для оценки ![]() и ковариационной матрицы
и ковариационной матрицы ![]() ошибок фильтрации, то есть строго
оптимальная оценка не может быть реализована на выходе дискретного линейного
фильтра Калмана (ФК).
ошибок фильтрации, то есть строго
оптимальная оценка не может быть реализована на выходе дискретного линейного
фильтра Калмана (ФК).
В данной задаче
возможно лишь получение квазиоптимальной текущей оценки состояния. В частности,
оценка ![]() может быть реализована с помощью
алгоритма обобщенного (расширенного) ФК (РФК). Известно [3], что РФК получается
на основе алгоритма линейного ФК при линейной аппроксимации нелинейных функций
наблюдений рядом Тейлора в точке известной текущей оценки состояния. В нашем
случае с учетом единичной матрицы перехода состояний
может быть реализована с помощью
алгоритма обобщенного (расширенного) ФК (РФК). Известно [3], что РФК получается
на основе алгоритма линейного ФК при линейной аппроксимации нелинейных функций
наблюдений рядом Тейлора в точке известной текущей оценки состояния. В нашем
случае с учетом единичной матрицы перехода состояний ![]() ,
соответствующей (3), уравнения фильтрации имеют вид [3]:
,
соответствующей (3), уравнения фильтрации имеют вид [3]:
![]() ;
; ![]() ; (5)
; (5)
![]() ;
(6)
;
(6)
![]() ,
(8)
,
(8)
где ![]() –
экстраполированная оценка состояния;
–
экстраполированная оценка состояния; ![]() – ковариационная матрица
ошибок экстраполяции;
– ковариационная матрица
ошибок экстраполяции; ![]() – матричный коэффициент
усиления фильтра;
– матричный коэффициент
усиления фильтра; ![]() – матрица Якоби (в данной
задаче – вектор производных сигнала наблюдения по координатам вектора
состояния). Экстраполированная оценка
– матрица Якоби (в данной
задаче – вектор производных сигнала наблюдения по координатам вектора
состояния). Экстраполированная оценка ![]() наблюдений
в уравнении (7) имеет вид
наблюдений
в уравнении (7) имеет вид
![]() .
(9)
.
(9)
Отметим два
обстоятельства, связанных с реализацией алгоритма (5) – (8). Во-первых, вычисление матрицы ![]() и
оценки
и
оценки ![]() выполняются приближенно на основе
линейной аппроксимации, что ведет к увеличению ошибок оценок состояния
при возрастании погрешности измерения ЧХ. И, во-вторых, сложность выражений,
определяющих функции в (4), приводит к существенному увеличению объема
вычислений при расчете матрицы
выполняются приближенно на основе
линейной аппроксимации, что ведет к увеличению ошибок оценок состояния
при возрастании погрешности измерения ЧХ. И, во-вторых, сложность выражений,
определяющих функции в (4), приводит к существенному увеличению объема
вычислений при расчете матрицы ![]() . Желание использовать
приближение второго порядка, как известно, требует расчета матрицы Гесса, что
приводит к дополнительным громоздким расчетам.
. Желание использовать
приближение второго порядка, как известно, требует расчета матрицы Гесса, что
приводит к дополнительным громоздким расчетам.
В связи с этим целесообразно применить, развитый авторами работы [4] метод приближенного вычисления среднего и ковариаций величин при многомерных нелинейных преобразованиях, который существенно сокращает объем вычислений. Применение этого метода к задаче фильтрации приводит к алгоритму UKF (unscented Kalman Filter).
Суть метода в том, что
для вычисления (оценки) моментов нелинейной функции ![]() используется
конечное множество точек («сигма-точки»);
используется
конечное множество точек («сигма-точки»); ![]() , где
, где ![]() – пространство состояний и
– пространство состояний и ![]() – его размерность. Выборка из «сигма-точек»
используется для расчета всех необходимых моментов вектор-функции
– его размерность. Выборка из «сигма-точек»
используется для расчета всех необходимых моментов вектор-функции ![]() по ее выборочным значениям на множестве
по ее выборочным значениям на множестве ![]() . Расположение точек в задаче фильтрации
на
. Расположение точек в задаче фильтрации
на ![]() -ом шаге определяется выражением
-ом шаге определяется выражением
![]() , (10)
, (10)
где ![]() –
– ![]() -й столбец матрицы
-й столбец матрицы ![]() ;
;
![]() ,
, ![]() –
составной параметр масштаба. Знак (+) в (10) принимаем для
–
составной параметр масштаба. Знак (+) в (10) принимаем для ![]() , и знак (–) для
, и знак (–) для ![]() .
Известно, что
.
Известно, что ![]() – квадратный корень из матрицы
(в данном случае симметрической) следует из ее представления в виде
– квадратный корень из матрицы
(в данном случае симметрической) следует из ее представления в виде
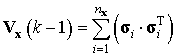 . (11)
. (11)
Для каждой «сигма-точки» (в данной
задаче на этапе прогноза наблюдения) вычисляется соответствующая точка в
пространстве наблюдений ![]() , то есть
, то есть
![]() .
(12)
.
(12)
Итоговая экстраполированная оценка наблюдений формируется в виде весового среднего по всем «сигма-точкам» (10)
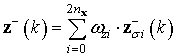 ,
(13)
,
(13)
где ![]() – вес
центральной (нулевой) точки
– вес
центральной (нулевой) точки ![]() ;
; ![]() ,
, ![]() –
весовые коэффициенты нецентральных точек.
–
весовые коэффициенты нецентральных точек.
Для расчета матриц ![]() и
и ![]() в этом
случае целесообразно использовать иную (эквивалентную) форму, которая связана с
вычислением ковариационной матрицы
в этом
случае целесообразно использовать иную (эквивалентную) форму, которая связана с
вычислением ковариационной матрицы ![]() обновляющего процесса
обновляющего процесса ![]() и ковариационной матрицы
и ковариационной матрицы ![]() . В итоге используются соотношения
. В итоге используются соотношения
![]() ;
(14)
;
(14)
![]() , (15)
, (15)
где необходимые для вычислений матрицы формируются по выборке из «сигма-точек» в виде
 ;
(15)
;
(15)
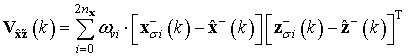 ;
(16)
;
(16)
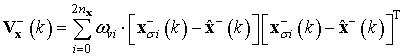 ,
(17)
,
(17)
здесь ![]() –
вес центральной (нулевой) точки;
–
вес центральной (нулевой) точки; ![]() для всех
для всех ![]() . Масштабный параметр
. Масштабный параметр ![]() и параметры
и параметры ![]() ,
, ![]() и
и ![]() обеспечивают
совпадение моментов ПРВ нелинейной функции
обеспечивают
совпадение моментов ПРВ нелинейной функции ![]() с
моментами аппроксимирующей ее гауссовой ПРВ. Детальный анализ по этому вопросу
выполнен в [4]. Оценка вектора состояния
с
моментами аппроксимирующей ее гауссовой ПРВ. Детальный анализ по этому вопросу
выполнен в [4]. Оценка вектора состояния ![]() выполняется
согласно (7).
выполняется
согласно (7).
3. Результаты моделирования и экспериментальных исследований
Проведено моделирование
разработанного алгоритма фильтрации. При моделировании канала предполагалось,
что из ![]() отсчетов ИХ только два отличны от нуля.
Отражатели размещались в соседних (рис. 2) или близких (рис. 3) элементах
разрешения по дальности. Комплексный коэффициент отражения (КО) первого
отражателя имел модуль, который линейно уменьшался с 1 до 0,5 при увеличении
номера отсчета частоты от 1 до
отсчетов ИХ только два отличны от нуля.
Отражатели размещались в соседних (рис. 2) или близких (рис. 3) элементах
разрешения по дальности. Комплексный коэффициент отражения (КО) первого
отражателя имел модуль, который линейно уменьшался с 1 до 0,5 при увеличении
номера отсчета частоты от 1 до ![]() . Фаза принята равной
0. Второй отражатель не имел частотно-зависимых свойств и его КО принят равным
1 на всех частотах.
. Фаза принята равной
0. Второй отражатель не имел частотно-зависимых свойств и его КО принят равным
1 на всех частотах.
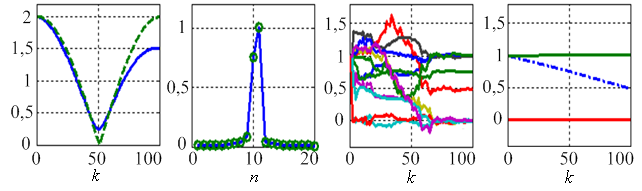
а) б) в) г)
Рис. 2. Результаты моделирования (СКО шума 0,001)
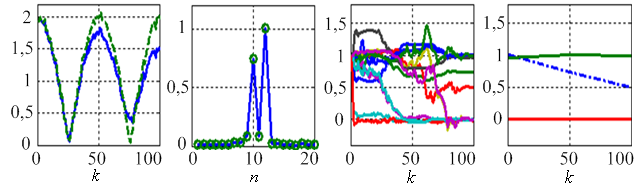
а) б) в) г)
Рис. 3. Результаты моделирования (СКО шума 0,05)
Для данных моделей на рис. 2а и 3а показаны модули измеренных ЧХ (пунктиром показаны ЧХ для постоянного и равного 1 модуля КО первого отражателя). На рис. 2б и 3б показаны соответствующие им ИХ. На рис. 2в и 3в показана сходимость оценок координат вектора состояния. Итоговые оценки частотных характеристик отражателей (зависимость действительной и мнимой частей от частоты, интерполированные по 3 точкам) изображены на рис. 2г и 3г. Показано, что при увеличении расстояния между отражателями увеличивается минимальное отношение сигнал/шум при котором оценки становятся состоятельными. Для получения результатов, показанных на рис. 2, среднеквадратическое отклонение (СКО) измерения квадратур принято равным 0,001. Результаты, представленные на рис. 3, получены при СКО шума равном 0,05.
Выполнена обработка экспериментальных измерений, полученных при помощи векторного анализатора цепей (ВАЦ) Agilent E8364B в коаксиальном тракте 7,0/3,04 мм в диапазоне частот от 10 МГц до 18 ГГц с шагом 10 МГц. В работе использован верификационный стандарт Битти. Двухпортовое устройство Битти представляет собой воздушную коаксиальную линию, внутренний проводник которой состоит из трех цилиндрических соосных секций различного диаметра с аксиальной симметрией и поперечной плоскостью отражения [5]. Крайние секции имеют волновое сопротивление 50 Ом, центральная – 25 Ом. Наличие двух скачкообразных изменений диаметра внутреннего проводника приводит к появлению отраженных волн, параметры которых зависят не только от величины изменения характеристического импеданса линии, но и от величины ступенчатой емкости (емкости разрыва), возникающей в месте скачка [6]. Также зависимость КО указанных неоднородностей от частоты обусловлена наличием потерь в подводящих линиях, которые возникают за счет скин-эффекта.
На рис. 4а показан модуль измеренной ЧХ стандарта Битти. На рис. 4б показан модуль ИХ, полученной при помощи обратного ПФ. Первый (24,946 мм) и второй (99,858 мм) пики ИХ обусловлены однократными отражениями от неоднородностей тракта. Остальные (в фильтре оцениваются ЧХ 6 отсчетов ИХ) являются результатом многократных переотражений. Геометрические размеры стандарта получены при помощи нутромера в составе с индикатором часового типа Mitutoyo 2109S-10 с ценой деления 1 мкм, насадкой 526-150 и мерой 7,000 мм; скобы рычажной с ценой деления 1 мкм совместно с концевыми мерами длины плоскопараллельными 3,04 и 4,615 мм; а также с помощью электронного микроскопа МР100 с линзой 50х.
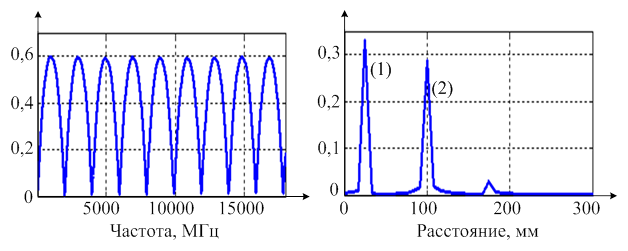
а) б)
Рис. 4. Модули частотной а) и импульсной б) характеристик стандарта Битти
Анализ точности выполним только для оценок ЧХ первых двух значимых отсчетов ИХ. Результаты показаны на рис. 5. Пунктирные линии соответствуют расчетным зависимостям модуля (логарифмический масштаб, дБ на рис. 5а) и фазы (в градусах на рис. 5б) КО неоднородностей. Сплошные линии – оценки ЧХ.

а) б)
Рис. 5. Сравнение расчетных значений и оценок ЧХ неоднородностей стандарта Битти
Как видно из поведения фазовой характеристики неоднородностей линии, положение скачка электрических параметров смещено относительно точки изменения геометрических размеров.
4. Заключение
Таким образом, в работе на основе модели канала с «блестящими» точками решена задача синтеза алгоритма, формирующего оценки частотных свойств отдельных отражателей. Показана работоспособность алгоритма, в том числе при обработке реальных измерений. Выделенные частотные характеристики отражателя можно использовать для реконструкции его формы или подробной идентификации электрических параметров.
1. Кеннеди Р. Каналы связи с замираниями и рассеянием. Пер. с англ. под ред. И.Е. Овсеевича. - М.: Сов. радио, 1973. - 302 с.
2. Савин А.А. Синтез квазиоптимального фильтра для оценки временного положения импульсного сигнала известной формы при многолучевом распространении радиоволн / Савин А.А., Тисленко В.И. // Известия вузов. Радиоэлектроника. – 2006. – № 6. – С. 56-61.
3. Сейдж Э., Мелс Дж. Теория оценивания и ее применение в связи и управлении. Пер. с англ. под ред. проф. Б.Р. Левина М.: Связь, 1976 – 496 с.: ил.
4. Julier S.J. and Uhlmann J.K. Unscented Filtering and Nonlinear Estimation, Proceedings of the IEEE, vol. 92, no. 3. March 2004, pp. 401 – 422.
5. Хибель М. Основы векторного анализа цепей / Михаэль Хибель. – пер. с англ. С.М. Смольского; под ред. У. Филипп. - М: Издательский дом МЭИ, 2009. - 500 с.: ил.
6. Somlo P.I. Computation of coaxial transmission line step capacitances // IEEE Trans. on Microwave Theory and Tech. – 1967. – vol. MTT–15, Jan., No. 1. – P. 48 – 53.