УДК 621.396.67

СИНТЕЗ ЗЕРКАЛ С ПРОСТРАНСТВЕННОЙ ДИСПЕРСИЕЙ КОЭФФИЦИЕНТА ОТРАЖЕНИЯ

С. Е. Банков

ИРЭ им. В.А. Котельникова РАН

Получена 1 декабря 2012 г.

Аннотация. Рассматривается задача синтеза формы двумерного зеркала, выполненного на основе отражающей поверхности с существенной зависимостью коэффициента отражения от угла падения. На основе модели поверхности в виде стенки с нелокальными импедансными граничными условиями определяется фаза отраженного поля, которая далее используется для синтеза формы зеркала, обеспечивающего требуемое преобразование волнового пучка. В качестве примера рассматривается синтез поверхности зеркала, преобразующего точечный источник в плоскую волну.

Ключевые слова: плоское зеркало, синтез формы зеркал, нелокальные импедансные граничные условия.

Abstract. A problem of synthesis of two dimensional mirror shape formed by a reflected surface with a sufficient dependence of reflection coefficient on angle of incidence is considered. A phase of the reflected field is determined in frame of model of the reflected surface as an impedance wall with non-local boundary conditions. The phase then is used for synthesis of mirror shape that provides the required transformation of wave field. A synthesis of mirror that transforms point source into plane wave is considered as an example.

Keywords: planar mirror, mirror shape synthesis, non-local impedance boundary conditions.

Постановка задачи

В последнее время большой интерес исследователей вызывают планарные квазиоптические структуры, которые выполняют функцию преобразования двумерных волновых пучков. Чаще всего такие структуры используются для создания планарных антенн миллиметрового диапазона (ММД). Под квазиоптическими структурами понимаются зеркала и линзы, которые функционируют аналогично зеркалам и линзам СВЧ и оптического диапазонов.

Среди примеров использования таких планарных структур можно отметить двухзеркальную антенну, построенную по схеме Кассегрена [1], в которой зеркала выполнены в виде EBG структуры из металлических цилиндров. В работе [2] рассмотрено планарное двухслойное зеркало, не имеющее эффекта затенения, которое также выполнено на основе решетки из металлических цилиндров. В работе [3] обсуждается планарная линза из метаматериала с принудительным преломлением.

Следует отметить, что планарные зеркала, выполненные из различных периодических структур, к которым относятся, в частности, EBG структуры имеют электродинамические свойства, существенно отличающиеся от свойств, например, идеально проводящей поверхности, которая традиционно используется в антенной технике для построения рефлекторов.

Основное отличие планарных отражающих структур проще всего видно на примере структуры с прямолинейной границей, которая возбуждается плоской волной, распространяющейся вдоль планарного волновода (ПЛВ). Отражатель с прямолинейной границей характеризуется коэффициентом отражения , который в общем случае является функцией угла падения . В случае отражателя в виде металлической стенки коэффициент отражения равен минус единице вне зависимости от угла падения. В тоже время, для планарных отражателей характерна существенная зависимость фазы коэффициента отражения от угла падения. Отметим, что при этом его модуль может оставаться равным, или, по крайней мере, близким к единице, что является следствием отсутствия потерь в отражателе.

Очевидно, что отраженное от планарного рефлектора поле в случае, когда оно не сводится к плоской волне или когда рефлектор имеет непрямолинейную границу, существенно отличается от поля отраженного от металлической границы. Поэтому зеркала традиционной формы: параболической, эллиптической, гиперболической и т.д. должны быть скорректированы с учетом отмеченного выше эффекта зависимости коэффициента отражения от угла падения. Данный эффект уместно назвать эффектом пространственной дисперсии коэффициента отражения по аналогии с пространственной дисперсией поверхностного импеданса [4]. Таким образом, целью данной работы является коррекция процедуры синтеза форма планарного зеркала с учетом эффекта пространственной дисперсии коэффициента отражения.

Следует также сказать, что пространственная дисперсия коэффициента отражения проявляется в более широком классе структур, чем пространственная дисперсия импеданса, хотя оба этих эффекта связаны друг с другом. В частности, поверхность с локальными импедансными граничными условиями уже имеет коэффициент отражения, зависящий от угла , хотя величина импеданса от него не зависит.

1. Модель планарного зеркала

На первом этапе обсудим модель планарного зеркала. Отметим, что планарное зеркало отражает двумерные волны, распространяющиеся в ПЛВ. ПЛВ может быть выполнен различным образом. Наиболее часто используемыми вариантами являются плоский волновод (ПВ) и планарный диэлектрический волновод (ПЛДВ). В первом случае речь идет о пластине с металлизированными поверхностями, в которой распространяются двумерные Т – волны. Во втором случае о диэлектрической пластине с поверхностными Е или Н – волнами.

Отметим известный факт, состоящий в том, что волны ПЛВ могут быть описаны как волны двумерной однородной среды с эффективной диэлектрической проницаемостью [4]:

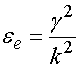, (1)

где - постоянная распространения волны ПЛВ, - волновое число свободного пространства. В двумерной среде могут распространяться волны Е и Н – типов. Тип волны в двумерной среде задается типом волны в исходном ПЛВ. Например, Т – волны эквивалентны Е – волнам двумерной среды. Мы ограничим наш анализ случаем Е – волн.

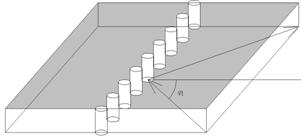
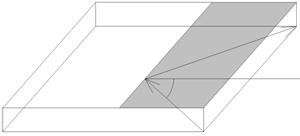
Планарный рефлектор может иметь весьма сложную структуру. На рис. 1 показаны несколько вариантов планарных отражателей с прямолинейной отражающей поверхностью.

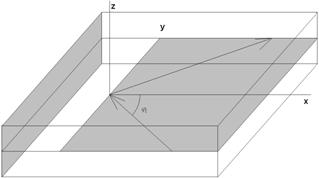
а б

Рис. 1. Планарные рефлекторы

Все избраженные на рис. 1 а – в структуры выполнены на основе ПВ. На рис. 1 а показан отражатель в виде периодической решетки из металлических цилиндров, на рис. 1 б в виде обрыва проводника ПВ, на рис. 1 в показано двухслойное планарное зеркало.

Для нас важно, что вне зависимости от структуры зеркала его реакция на падение плоской волны с углом падения может быть описана в виде коэффициента отражения , модуль которого мы полагаем равным единице. Фаза коэффициента отражения зависит от положения отсчетной плоскости. Строго говоря, отраженное поле не зависит от положения отсчетной плоскости. Однако на практике ее целесообразно выбирать так, чтобы минимизировать зависимость фазы коэффициента отражения от угла падения.

Далее найдем отраженное поле в более общем случае, когда падающее поле имеет произвольный вид. Для этого представим его в виде интеграла Фурье:

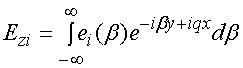, (2)

где - спектральная плотность падающего поля. Отсчетная плоскость расположена при .

Учитывая, что каждая парциальная плоская волна из разложения (2) отражается с коэффициентом отражения , то для отраженного поля получаем следующее выражение:

. (3)

Спектральный параметр связан с углом падения следующим образом:

. (4)

Запишем отраженное поле непосредственно в отсчетной плоскости:

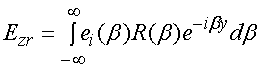. (5)

Выразим функцию через падающее поле при :

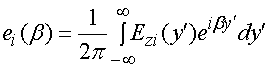. (6)

Подставим формулу (6) в (5):

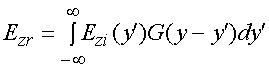, (7)

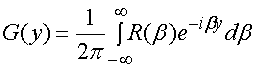. (8)

Выражение (7) является интегральным представлением отраженного поля. Если функция постоянна, то есть не зависит от угла падения, то ядро интегрального представления превращается в дельта функцию, а отраженное поле определяется значением падающего поля в точке наблюдения. В общем случае функция отлична от дельта функции и выражение (7) описывает нелокальную связь отраженного и падающего полей.

Учтем далее особенность поля в квазиоптических устройствах, которыми являются планарные зеркала. Она состоит в том, что спектр, так называемой геометрооптической части поля всегда ограничен следующим интервалом:

, (9)

Ограничение спектра поля интервалом (9) означает, что мы исключаем из анализа реактивные затухающие волны, как правило, локализованные вблизи источника. Поскольку в квазиоптических устройствах расстояние от источника до отражателя весьма велико, то вклад указанных волн пренебрежимо мал и принятое допущение вполне оправданно. С учетом сделанных замечаний мы можем модифицировать выражение (8):

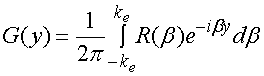. (10)

Нам теперь осталось обобщить соотношение (7) для случая изогнутой поверхности рефлектора.

Введем, как показано на рис. 2 локальную систему координат , связанную с поверхность рефлектора.

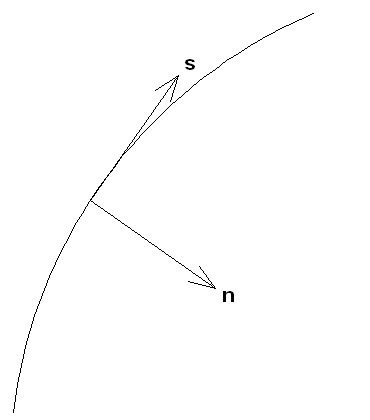
Рис. 2. Локальная система координат

Во введенной системе координат соотношение (7) записывается следующим образом:

. (11)

Выражение (11) справедливо только для поверхностей с большим радиусом изгиба, при котором соотношение (8) остается в силе. Важно, что именно такие поверхности используются для построения квазиоптических зеркал.

2. Анализ отраженного поля

Продолжим во втором разделе анализ отраженного поля с помощью соотношения (11). На первом этапе рассмотрим на типичном примере поведение функции .

В качестве отражающей структуры используем диэлектрический слой, расположенный на металлической поверхности. Его коэффициент отражения записывается следующим образом [5]:

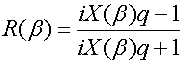, (12)

где - относительная диэлектрическая проницаемость слоя, а - его толщина. Для простоты полагаем, что эффективная проницаемость среды, в которой расположена отражающая структура равна единице.

На рис. 3 показана зависимость модуля функции , нормированного на его значение в точке . Кривые 1 – 3 получены для =4, 4.5, 5, , ГГц.

Видно, что функция достаточно сильно локализована в окрестности точки . При увеличении толщины слоя степень локализации уменьшается.

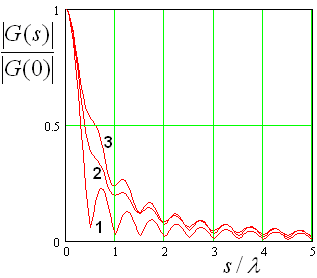
Рис. 3. Ядро интегрального оператора

Такое поведение ядра интегрального оператора (11) позволяет нам использовать для описания поля разложение в ряд Тейлора в окрестности точки . При этом мы будем отдельно рассматривать модуль и фазу поля:

. (13)

Целесообразность выделения модуля и фазы поля обусловлена тем, что модуль поля на поверхности зеркала, как правило, меняется значительно медленнее фазы. Поэтому с учетом локализации ядра интегрального оператора мы можем считать его постоянным:

. (14)

Фазу падающего поля представим в виде разложения в ряд Фурье:

, (15)

где и - первая и вторая производные от фазы в точке .

Оставим в разложении (15) три первых члена. Отметим, что производная от фазы падающего поля с геометрооптической точки зрения [6] связана с касательной компонентой волнового вектора луча, падающего на зеркало в точке с координатой :

. (16)

Введем также обозначение:

. (17)

Запишем далее выражение (11) с учетом сделанных преобразований:

. (18)

Представим второй экспоненциальный множитель в формуле (18) в виде ряда:

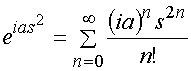. (19)

Интеграл, стоящий в правой части выражения (18) можно преобразовать следующим образом:

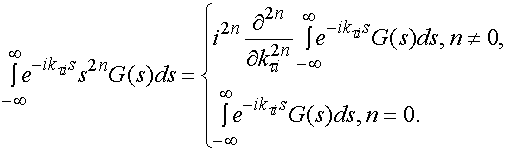. (20)

С учетом соотношений (8), (19) и (20) формула (18) принимает следующий вид:

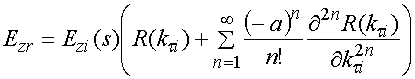. (21)

Первое слагаемое в формуле (21) соответствует геометрооптическому описанию поля. В соответствии с ним отраженное поле равно падающему, умноженному на коэффициент отражения. При этом коэффициент отражения берется для угла падения, равного углу падения луча, падающего на зеркало в данной точке его поверхности. Добавка к геометрической оптике описывается суммой, в которую входят производные от коэффициента отражения.

Для удобства использования в выражении для фазы отраженного поля можно выделить в явном виде фазу падающего поля:

, (22)

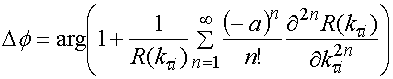где - фаза коэффициента отражения.

3. Синтез фокусирующего рефлектора

Применим полученное соотношение (21) для решения задачи синтеза фокусирующего рефлектора из поверхности с коэффициентом отражения (12).

Процедура синтеза поясняется на рис. 4. Точка является точкой фокуса, в которую должны сходиться лучи, отраженные от рефлектора при падении на него плоской волны, распространяющейся вдоль оси .

Пусть в фокусе рефлектора расположен точечный источник, облучающий зеркало. Потребуем выполнения условия для фазы отраженного поля, обеспечивающего преобразование волны точечного источника в плоскую волну. Для этого нам необходимо учесть, что

. (23)

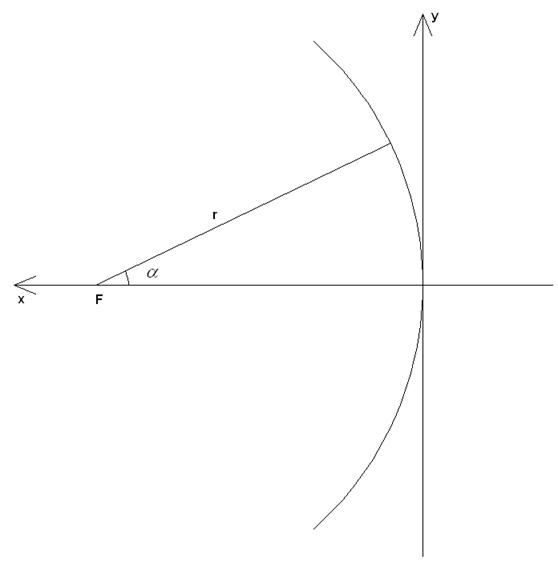
Рис. 4. Синтез поверхности фокусирующего рефлектора

Принимая во внимание соотношение (23), получаем:

. (24)

Из формулы (24) находим радиус :

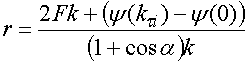. (25)

Соотношение (25) записано с учетом того, что при , луч падает на зеркало по нормали, то есть . В отсутствие зависимости фазы от падающего поля уравнение (25) совпадает с уравнением параболического рефлектора [6].

Отметим, что выражение (25) является трансцендентным уравнением относительно радиуса , так как фаза зависит от компоненты волнового вектора , которая, в свою очередь, связана с углом и радиусом . Несложные геометрические построения позволяют получить указанную связь:

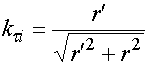, (26)

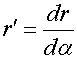Из формул (26) видно, что в уравнение (25) входит производная от радиуса по углу. Для решения задачи синтеза нами использовалась следующая итерационная схема:

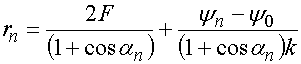, (27)

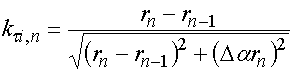Шаг итерационной схемы выбирается в ходе численных экспериментов. В качестве начальных условий использовались следующие соотношения:

, (28)

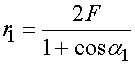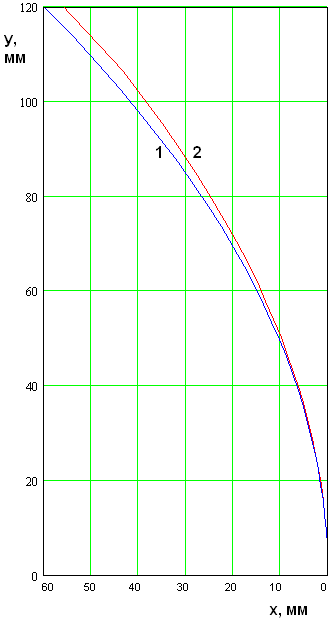
Рис. 5. Синтезированный фокусирующий рефлектор

На рис. 5 показан профиль синтезированного рефлектора (кривая 2), полученный при , , ГГц, мм. Кривая 1 соответствует профилю параболического зеркала с тем же фокусным расстоянием. Нетрудно увидеть, что отличие двух зеркал особенно при больших углах может быть весьма существенным.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект № 12-08-12003/12 офи_м.

Литература

1. M. Ettorre, S. Bruni, G. Gerini, A. Neto, N. Llombart, S. Maci, Sector PCS-EBG Antenna for Low Cost High Directivity Applications, Antennas and Wireless Propagation Letters, Vol.6, pp. 537-539, Dec. 2007.

2. Банков С.Е., Весник М.В. Квазиоптический возбудитель антенной решетки на основе EBG структуры // РЭ. 2009. Т. 54. № 11, С. 1256-1266.

3. Bankov S.E., Douplenkova M.D., Kalinichev V.I., Kozin V.N., Levchenko I.V., Kuranov U.V., Rodionova E.V., Vasjukov V.D. 60 GHz Sensors Based on Dielectric Slotted Waveguide // 22nd European Microwave Conf. Proc. of Workshop “Commercial Applications of Microwave and Millimeter Waves”, 1992, p.p. 41-46.

4. Банков С.Е. Волноводы с нелокальными границами // Журнал радиоэлектроники [электронный журнал]. 2008. № 6. URL: http://jre.cplire.ru/iso/jun08/5/contents.html.

5. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. М.: Радио и связь. 1983.

6. Корнблит С. СВЧ оптика. Оптические принципы в приложении к конструированию СВЧ антенн. М.: Связь. 1980.