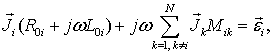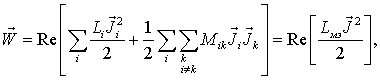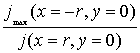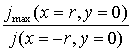Расчет индуктивности колец при произвольной степени скин-эффекта.

УДК 621.396

РАСЧЁТ ИНДУКТИВНОСТИ КОЛЕЦ ПРИ ПРОИЗВОЛЬНОЙ СТЕПЕНИ СКИН-ЭФФЕКТА

А. В. Савельев, Н. П. Чубинский

Московский физико-технический институт (государственный университет)

Статья получена 23 декабря 2013 г.

Аннотация. Предложен алгоритм расчёта индуктивностей колец при произвольной степени скин-эффекта. Он основан на определении трёхмерных распределений плотности тока по сечению кольца. Это позволило корректно определять индуктивности «толстых» колец, радиус которых всего в несколько раз превышает толщину проводника, во всём диапазоне частот применимости квазистатического приближения. Предполагается использовать данный метод для расчёта взаимной индуктивности сильно связанных «толстых» контуров. Полученные результаты для тонких колец хорошо согласуются с известными асимптотическими расчётами. Использованный алгоритм дал возможность определять эффективные индуктивности и сопротивления колец, образованных системой тонких изолированных проводников.

Ключевые слова: индуктивность, скин-эффект, распределение плотности токов

Abstract: The algorithm of the inductance rings calculation is offered at any degree of skin effect. It is based on definition of three-dimensional distributions of the current density on section of a ring. It has allowed to determine correctly inductance of "thick" rings when its radius only in some times exceeds thickness of a conductor. The algorithm works in all frequency range of applicability quasistatic approximation. It is supposed to use the given method for calculation of mutual inductance of strongly connected "thick" contours. The received results for thin rings will well be coordinated with known asymptotic calculations. The used algorithm has enabled to determine effective inductance and resistance of the rings formed by system of thin isolated conductors.

Keywords: inductance, skin effect, distributions of the current density.

1. Введение

Распределение плотности переменного тока по сечению проводников неравномерно. Это явление, известное под названием скин-эффекта, приводит к тому, что значения индуктивностей и активного сопротивления, например, круглого кольца при высокочастотном поле, отличаются от их значений при низкой частоте. Так как явление скин-эффект усиливается с ростом частоты тока, то при расчете его индуктивности и активного сопротивления различают случай низкой частоты, случай высокой частоты и предельный случай весьма высокой частоты [1]. В данном случае индуктивность и сопротивление кольца являются сосредоточенными радиотехническими элементами, то есть их размеры должны быть много меньше длины волны электромагнитного поля. Первое аналитическое определение индуктивности круглого кольца при равномерном распределении плотности тока по сечению проводника дано Рэлеем [2], а для случая сильного скин-эффекта – получено Фоком [3]. Асимптотические решения для разнообразных форм контуров даны в [1,4] только для двух крайних случаев: равномерного распределения плотности тока в проводнике (низкочастотное приближение) и для сильного скин-эффекта (высокочастотное приближение, когда ток распределён в его тонком поверхностном слое). Решение Фока хорошо работает только для круговых достаточно «тонких» колец, радиус которых значительно больше радиуса проводника . Особый интерес представляет случай, когда радиус кольца незначительно превышает радиус проводника. Такие элементы слабо исследованы, хотя находят широкое применение в радиоаппаратуре СВЧ диапазона и при создании искусственных сред с эффективной магнитной проницаемостью менее единицы [5].

2. Цель работы и алгоритм решения задачи

Работа посвящена изучению влияния скин-эффекта на импеданс кольца круглого сечения для всего частотного диапазона, удовлетворяющего условиям квазистатики:

, (1)

где – длина волны.

Рассмотрим проводящее кольцо круглого сечения (тор), возбуждаемое источником единичной э.д.с. с частотой . Геометрия сечения кольца дана на Рис. 1. Для расчета распределения плотности тока в квазистатическом приближении по сечению кольца при разных уровнях скин-эффекта сечение кольца разбивается на множество колец круглого сечения, внутри которых распределение токов можно считается равномерным.

Рис. 1. Геометрия задачи

Поскольку при сильном скин-эффекте плотность тока в кольце по направлению к границе провода нарастает, то целесообразно использовать разбиение, которое становится более подробным ближе к поверхности проводника. Разбиение строится послойно (Рис. 2) следующим образом: в каждом следующем слое, начиная со второго, число элементов удваивается (исключение составляет только центральный элемент и первый слой из 6-ти элементов). Коэффициент, определяющий число колец в каждом следующем слое, может быть выбран другим , в том числе и дробным, в зависимости от геометрии задачи и оценочной степени неравномерности плотности тока. Центры элементов разбиения в каждом слое равноудалены от центра сечения кольца. Радиусы элементов подобраны такими образом, чтобы они были согласованы с радиусом провода (в сумме давали радиус провода). В данной работе используется 8 слоев, что соответствует 763 элементам разбиения.

Рис.2 Неоднородное разбиение сечения кольца

Пронумеровав элементы, запишем систему линейных уравнений, описывающих распределения токов в квазистатическом приближении:

, (2)

где – комплексная амплитуда тока в -ом элементе, – импеданс, а – индуктивность -го элемента на низкой частоте, – радиус -го элемента, – удельное сопротивление материала, – индуктивность -го элемента, – «эффективная» площадь сечения элемента, равная отношению площади сечения слоя (концентрического кольца на Рис. 2) к числу элементов в нем. – комплексная амплитуда э.д.с. в -ом элементе (в данном случае 1 В), – сумма э.д.с., вносимых в -тый контур из всех остальных контуров, – взаимные индуктивности и

– (3)

активные сопротивления элементов. Классические алгоритмы расчета собственных и взаимных индуктивностей приведены в [1].

Решение данной системы уравнений определяет распределение плотности тока в сечении кольца. На основе этих данных можно определить индуктивность кольца , используя выражения для реактивной энергии системы токов в элементах разбиения [6]:

(4)

где – полный ток через сечение кольца.

Вычислим эквивалентное сопротивление системы , приравняв мощность потерь, вычисленную как сумму мощностей потерь во всех элементах:

(5)

Можно вычислить индуктивность и сопротивление кольца другим способом. Просуммировав полученные выше токи в каждом из элементов разбиения, получим полный ток и вычислим импеданс кольца:

(6)

Конечным результатом данной работы будет сравнение модельных значений и , полученных энергетическим методом, и и , полученных из соотношения (6), со значениями, рассчитанными по классическим формулам в [1]:

– (случай низкой частоты), (7)

– (случай весьма высокой частоты). (8)

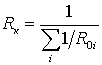– (сопротивление на постоянном токе) (9)

Определим существенные моменты для численного моделирования. Выполнение условий квазистатического приближения (1) даёт ограничение на максимальную частоту в численном эксперименте: [Гц]

[Гц][м]. (10)

Для выбранной частоты диаметр элементов внешнего слоя разбиения должна быть по крайней мере в два раза меньше толщины скин-слоя. При оценках толщины скин-слоя в медном проводе использована формула для проводящего полупространства – [м].

Максимальные частоты в численном эксперименте должны удовлетворять соотношению (10). Например, для радиуса кольца =0,01 м она не должна превышать 480 МГц, а для =10 м – 480 кГц. Радиус провода везде равен 3,33 мм. Верхняя частота, использованная в расчётах, равна 100 кГц, при которой для всего диапазона радиуса кольца выполнены условия квазистатики, а также условия на величину диаметра элементов внешнего слоя разбиения. Моделирование проведено для следующих частот и радиусов колец:

1 Гц, 10² Гц, 10³ Гц, 10⁴ Гц и 10⁵ Гц;

0,01 м, 0,1 м и 10 м, что соответствует отношению =3, 30 и 3000.

3. Результаты расчёта индуктивности колец, возбуждаемых внешней э.д.с. (классический случай)

На основании расчётов определены трёхмерные распределения плотности токов в сечении кольца. На графиках Рис.3 представлены срезы нормированных распределений плотностей токов в плоскости (0).

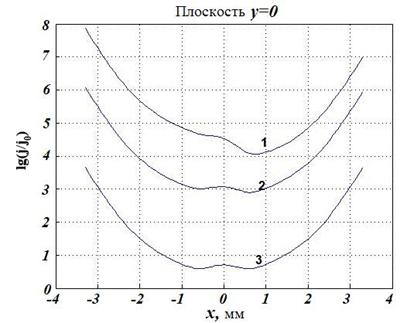
Рис.3. Распределение плотности тока по сечению кольца в классическом случае для разных относительных радиусов кольца :
1 – =3, 2 – =30, 3 – =3000 – при частоте 10⁵Гц

Параметр дан для постоянного тока и считается константой для каждого диаметра кольца. Результаты получены для различных соотношений между радиусом провода и радиусом кольца : 3, 30 и 3000 – при фиксированной частоте 10⁵ Гц. Кривые распределения плотности тока соответствуют сильному скин-эффекту. С уменьшением параметра распределение становится всё более асимметричным – 1 при =3, а его минимум всё более смещается к внешней поверхности кольца.

В Таблице 1 приведены количественные параметры распределения плотности тока для ряда относительных радиусов кольца на частоте 10⁵Гц, соответствующие Рис. 3. Первым параметром является коэффициент асимметрии, равный отношению плотностей тока на внутренней и внешней поверхностях кольца , вторым – относительное смещение минимума плотности тока и третьим – отношение максимальной плотности тока к минимальной – .

Таблица 1.

		Смещение минимума плотности тока,	Отношение максимальной плотности тока к минимальной,
3	7,66	0,207	6502
30	1,39	0,170	1513
3000	1,001	£0,03	1160

Эффективная толщина скин-слоя из-за асимметрии распределения тока различается в небольших пределах на внутренней и внешней поверхностях кольца. Например, на внутренней поверхности кольца – =0,22 мм при всех радиусах кольца, а на внешней – монотонно увеличивается с уменьшением отношения радиусов кольца к радиусу проводника – ³0,22 мм. Для весьма толстого кольца ³3 наблюдается его увеличение более, чем на 5 %. При этом толщина скин-слоя в кольце очень близка к его толщине для плоской границы проводника (около 0,21 мм).

На Рис.4 представлены распределения плотностей токов в плоскости сечения толстого кольца (=3) для ряда частот (10⁵ Гц, 10⁴ Гц и 10³ Гц). Они асимметричны, а их минимумы с уменьшением частоты смещаются к внешней поверхности кольца. Глубина минимумов уменьшается, и распределение становится монотонно убывающим к внешней поверхности кольца, а перепад плотности тока в плоскости стремится при к величине .

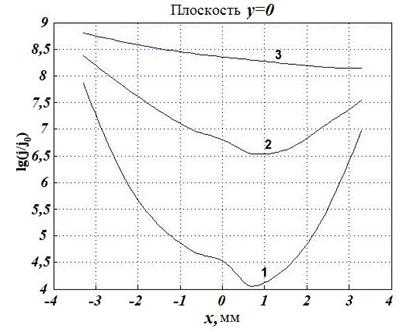
Рис.4. Распределение плотности тока по сечению кольца для ряда частот:
1 – 10⁵Гц, 2 – 10⁴Гц, 3 – 10³Гц при =3

В Таблице 2 даны основные параметры распределения токов в толстом кольце (3) для трёх частот, соответствующие Рис. 4, а в Таблице 3 приведены эффективные толщины скин-слоя при тех же частотах на внутренней и внешней поверхностях кольца. В последнем столбце даны те же величины для плоской границы проводника.

Таблица 2.

кГц
100	7,66	0,207	6502
10	6,99	0,273	71,1
1	4,64	0,943	4,65

Таблица 3.

кГц	, мм	, мм
100	0,22	0,23	0,21
10	0,82	0,56	0,66
1	3,28	–	2,11

По результатам расчётов определены отношения величин индуктивностей и сопротивлений кольца для нескольких значений частоты и параметра (Таблица 4), которые были получены энергетическим методом и методом

Таблица 4.

Гц	, м
1	2	3	4	5	6	7	8
1	0,01	3	0,9551	1,3218	1,0000	0,9551	1,3218
	0,1	30	1,0008	1,0746	1,0000	1,0008	1,0746
	10	3000	1,0005	1,0314	1,0000	1,0005	1,0314
10²	0,01	3	0,9536	1,3198	1,0032	0,9545	1,3210
	0,1	30	1,0006	1,0744	1,0014	1,0007	1,0744
	10	3000	1,0005	1,0314	1,0013	1,0005	1,0314
10³	0,01	3	0,8788	1,2162	1,2302	0,9203	1,2736
	0,1	30	0,9891	1,0620	1,1249	0,9964	1,0698
	10	3000	0,9956	1,0264	1,1201	0,9987	1,0296
10⁴	0,01	3	0,7592	1,0507	3,1861	0,7955	1,1009
	0,1	30	0,9454	1,0151	2,8186	0,9586	1,0292
	10	3000	0,9762	1,0064	2,7981	0,9821	1,0124
10⁵	0,01	3	0,7320	1,0130	9,4187	0,7439	1,0295
	0,1	30	0,9358	1,0048	8,3049	0,9401	1,0094
	10	3000	0,9720	1,0021	8,2379	0,9739	1,0040

вычисления полного импеданса, к значениям индуктивностей и сопротивлений, вычисленных по классическим формулам (7), (8) и (9). В ней приняты следующие обозначения:

– значение индуктивности, полученное энергетическим методом (4),

– значение сопротивления, полученное из (5),

– значения индуктивностей, полученных по классическим формулам на низкой (7) и весьма высокой (8) частотах, соответственно,

– значения сопротивления на постоянном токе (9),

индуктивность и активное сопротивление, полученное из (6).

Результаты 4-го столбца Таблицы 4 наглядно показывают, что классическая формула (7) для индуктивности на низких частотах ощутимо завышает её величину на частотах больших 100 Гц. Наибольшие завышения соответствуют толстому кольцу (3), которые растут с увеличением частоты и достигают 27% при =100 кГц. В 5-м столбце сравниваются результаты моделирования со значениями индуктивности, полученными для сильного скин-эффекта (8). Здесь наблюдается занижение, уменьшающееся с увеличением частоты, в области частот ниже 10 кГц это расхождение более 20% для толстых колец. Уменьшение относительного радиуса кольца увеличивает расхождение, величина которого не превышает 1…2% для толстого кольца (3 при =100 кГц). В 6-м столбце наблюдается достаточно очевидное увеличение активного сопротивления кольца при увеличении частоты. Причём и здесь толстое кольцо заметно отличается от тонких. Его сопротивление более чем на 10% выше. В 7-м и 8-м столбцах модельные величины индуктивности, найденными по значениям импеданса кольца (6), сравниваются с рассчитанными по классическим формулам (7) и (8). Здесь для колец большого радиуса () наблюдается незначительное завышение и занижение, соответственно. Но для толстого кольца происходит резкое увеличение расхождений с классическими расчётами, уменьшающееся с ростом частот. При сильном скин-эффекте (=100 кГц) наблюдается небольшое расхождение между результатами использования энергетического и импедансного методов (колонки 5 и 8).

4. Результаты расчёта эффективной индуктивности колец, образованных тороидальной системой изолированных кольцевых элементов, во внешнем переменном магнитном поле

Рассмотрим систему плотно упакованных изолированных проводящих кольцевых элементов, образующих тор, в переменном магнитном поле, вектор индукции которого ортогонален плоскости кольца (Рис. 1) и изменяется гармонически с частотой . Такие кольца со сложной геометрией используют в качестве элементов подстройки резонансной частоты контуров мощных передатчиков СДВ, ДВ и СВ диапазонов. Выполнение условия квазистатического приближения определено неравенством (1).

Для расчета распределения плотности тока используем рассмотренную выше модель сечения и алгоритм расчёта. В квазистатическом приближении сечение кольца при разных уровнях скин-эффекта представляет собой множество изолированных колец круглого сечения, внутри которых распределение токов можно считается равномерным.

При проведении вычислении в системе уравнений (2) фиксированная э.д.с. внешнего источника заменена набором э.д.с., возбуждаемых внешним магнитным полем с индукцией и зависящих от радиуса элементарного кольцевого элемента :

(11)

На графиках Рис.5 представлены срезы трёхмерного распределения эффективной плотности тока в плоскости сечения кольца . Результаты получены для тех же соотношений между радиусами кольца и провода: 3, 30 и 3000 – при фиксированной частоте 10⁵Гц. Кривые распределения плотности тока соответствуют сильному скин- эффекту, с уменьшением параметра они становятся всё более асимметричными – 1 при =3, а их минимумы всё более смещаются теперь к внутренней поверхности кольца .

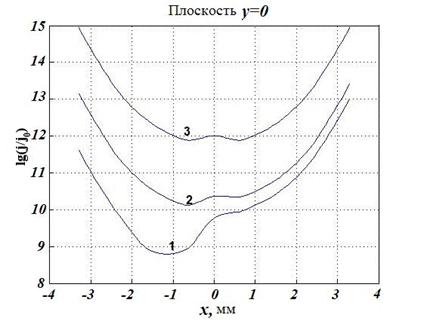
Рис.5. Распределение плотности тока по сечению кольца для следующих значений параметра :
1 – =3, 2 – =30, 3 – =3000 при 10⁵ Гц

В Таблице 5 приведены количественные соотношения, соответствующие Рис. 5. Асимметрия распределения токов стремится к нулю при увеличении относительного радиуса кольца, в пределе такое распределение соответствует прямолинейному проводнику. С уменьшением параметра (<10) коэффициент асимметрии резко возрастает. Смещение минимума плотности тока происходит в сторону внутренней поверхности кольца и увеличивается с уменьшением параметра . При этом отношение максимальной плотности тока к минимальной увеличивается более чем в 14 раз.

Таблица 5.


3	24,5	-0,351	16368
30	1,83	-0,195	1990
3000	1,015	-0,0042	1169

Асимметрия распределения тока приводит, как и в первом случае возбуждения, к незначительной разнице эффективной толщины скин-слоя на внутренней и наружной поверхностях кольца.

На графиках Рис.6 представлены срезы трёхмерного распределения эффективной плотности тока в сечении кольца для различных частот (10⁵ Гц, 10⁴ Гц и 10³ Гц) при фиксированном параметре =3. С уменьшением частоты в распределении токов исчезает минимум и оно монотонно растёт от внутренней поверхности кольца к внешней, а величина перепада стремится при к .

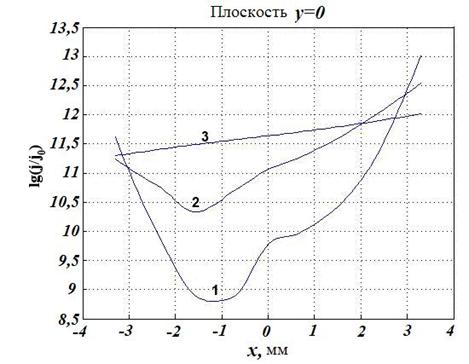
Рис.6. Распределение плотности тока по сечению кольца для разных частот:
– 10⁵ Гц, 2 –10⁴ Гц, 3 –10³ Гц; (a=)

В таблице 6 представлены частотные зависимости основных параметров распределения плотности токов в сечении кольца, соответствующие Рис.6. Поведение функций распределения токов качественно совпадают с результатами предыдущего раздела (Таблица 2). Однако асимметрия распределения плотности тока здесь заметно выше, смещение его минимума происходит в другую сторону (к внутренней поверхности кольца), а перепад значений этой функции на порядок больше.

Таблица 6.

кГц
100	24,5	-0,351	16368
10	19,7	-0,474	162
1	5,21	-0,998	5,21

В Таблице 7 показаны частотные зависимости эффективной толщины скин-слоя. Наблюдается существенно большая асимметрия, обусловленная увеличением асимметрии в распределении плотности тока, по сравнению со случаем возбуждении кольца сторонней э.д.с.

Таблица 7.

кГц	, мм	, мм	, мм
100	0,22	0,51	0,21
10	0,28	1,6	0,66
1	–	2,91	2,11

По результатам расчётов определены отношения величин эффективных индуктивностей и сопротивлений кольца, образованного системой изолированных проводящих кольцевых элементов, для нескольких значений частоты и параметра (Таблица 8), которые были получены энергетическим методом, к значениям индуктивностей и сопротивлений, вычисленных по классическим формулам (7), (8) и (9).

Общий взгляд на результаты 4-го и 5-го столбцов Таблицы 8 наглядно показывает, что для достаточно больших колец () они для всех частот отличаются не более чем на 7% от значений, полученных по классическим формулам (7) и (8). Для всех частот (1…10⁵) Гц при уменьшении параметра нарастает расхождение между найденными здесь значениями индуктивности с результатами классических формул. Особенно резко увеличивается расхождение для толстого кольца =3, так результаты 5-го и 6-го столбцов указывают, что значения индуктивности и сопротивления увеличиваются почти вдвое на частоте 100 кГц, что существенно большее, чем в предыдущем случае возбуждения.

Таблица 8.

Гц	, м
1	2	3	4	5	6
1	0,01	3	1.0574	1.4634	1.1133
	0,1	30	1.0015	1.0753	1.0010
	10	3000	1.0005	1.0314	1.0000
10²	0,01	3	1.0581	1.4644	1.1205
	0,1	30	1.0014	1.0752	1.0028
	10	3000	1.0005	1.0314	1.0013
10³	0,01	3	1.1267	1.5593	1.6349
	0,1	30	0.9928	1.0659	1.1493
	10	3000	0.9956	1.0264	1.1201
10⁴	0,01	3	1.2835	1.7763	5.0828
	0,1	30	0.9572	1.0277	2.9307
	10	3000	0.9762	1.0064	2.7982
10⁵	0,01	3	1.3145	1.8191	15.4914
	0,1	30	0.9495	1.0195	8.6721
	10	3000	0.9720	1.0021	8.2381

5. Выводы

1. Построен алгоритм расчёта индуктивностей колец при произвольной степени скин-эффекта. Он наиболее эффективен при вычислении индуктивностей (а так же сопротивлений) толстых колец, когда известные асимптотические приближения имеют большие погрешности.

2. Алгоритм основан на замене сечения кольца системой тонких контуров, в которых распределение плотности тока считается равномерным, и решении системы уравнений, описывающих неоднородное распределение тока. Использование существенно неравномерного разбиения сечения кольца, качественно учитывающее особенности скин-эффекта, многократно повышает его продуктивность.

3. Показано, что распределение плотности тока в сечении кольца становится всё более асимметричным по мере уменьшения его радиуса. Минимум этого распределения смещается к внешней поверхности кольца при возбуждении его источником э.д.с.

4. Асимметрия распределения тока в сечении кольца приводит к существенным погрешностям в определении его индуктивности, которые могут превышать для «толстых колец» 20…30 % при определённых уровнях скин-эффекта.

5. Результаты для индуктивности и сопротивления кольца наибольшего радиуса (=3000) асимптотически приближаются к аналитическому решению для прямолинейного провода.

6. Для «толстых» колец тороидальной формы, образованных системой плотно уложенных изолированных проводников и возбуждаемых внешним магнитным полем, расхождения результатов классических расчетов эффективных индуктивности и сопротивления почти вдвое выше, чем для случая классического возбуждения источником э.д.с.

Литература

1. П.Л. Калантаров, Л.А. Цейтлин. Расчет индуктивностей: Справочная книга. – Л.: Энергоатомиздат. Ленингр. отд., 1986. – 488 с.

2. Ravleigh, S.D.W.. Proceedings of Royal Society, 32, p. 104 (1881); 86, p. 562 (1912).

3. В. А. Фок. Журнал Русского Физико-Химического общества, часть физическая, 62, № 3 (1930).

4. Цейтлин Л.А. Индуктивности проводов и контуров. – Л.: Госэнергоиздат, 1950 – 228 с.

5. Shelby R. A., Smith D. R. and Schulz S. Experimental Verification of Negative Index of Refraction. –Science. – 2001. – V. 292. – P. 77-79

6. В.В. Никольский, Т.И.Никольская. Электродинамика и распространение радиоволн: Учеб. Пособие для вузов – М.: Наука. Гл. ред. физ-мат. лит.,1989 – 544 с.