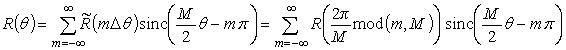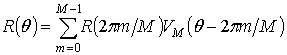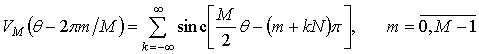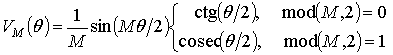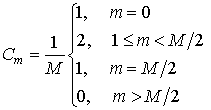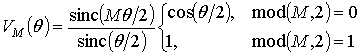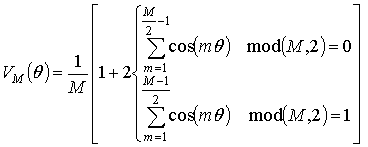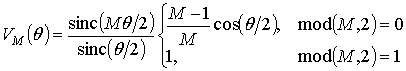Особенности интерполяции 2π-периодических функций с финитным спектром Фурье
на основе теоремы отсчетов
 

И. С. Дмитриев, М. П. Сличенко

ОАО «Концерн «Созвездие», г. Воронеж

Статья получена 23 декабря 2013 г.

 

Аннотация. Получено точное замкнутое выражение, позволяющее вычислять значения 2π-периодической функции с финитным спектром Фурье, а также ее производной произвольного порядка в произвольной точке в виде конечной взвешенной суммы отсчетов функции на ее периоде. Проанализировано ядро полученного разложения.

Ключевые слова: периодическая функция, финитный спектр, интерполяция, теорема отсчетов.

Abstract. The exact closed expression is received, allowing to calculate values of 2π-periodic function with a finite spectrum Fourier, and also its derivative of a random order in an arbitrary point in the form of the final weighed sum of references of function on its phase. The kernel of the received expansion is analysed.

Keywords: periodic function, finite spectrum, interpolation, the sampling theorem.

 

Во многих областях науки и техники существует задача восстановления непрерывной достаточно гладкой функции угловой координаты с областью определения  по ее дискретным отсчетам, т.е. значениям функции в некоторых, в частном случае эквидистантных, точках области определения. Такая задача актуальна, например, в антенной технике при экспериментальном измерении диаграмм направленности антенных систем, и особенно – в радиопеленгации, когда оценка пеленга получается путем максимизации некоторой решающей функции (см., например, [1]). В последнем случае для применения численных методов оптимизации желательно иметь аналитическое выражение не только самой решающей функции, но и хотя бы первой ее производной. Для вычисления такой функции необходимо априорное знание характеристик данной антенной системы в реальном окружении, рассчитанных методами вычислительной электродинамики или измеренных экспериментально и представленных в виде таблицы. То есть значения максимизируемой функции, по форме аналогичной некоторой диаграмме направленности, могут быть непосредственно рассчитаны на практике только в дискретном множестве табличных точек, и для отыскания ее максимума необходимо корректно интерполировать функцию на интервалах между табличными точками.

Можно показать, что любая физически реализуемая решающая функция или диаграмма направленности  удовлетворяет необходимым условиям применимости теоремы отсчетов Котельникова [2] при условии ее бесконечного периодического продолжения в обе стороны от области определения. Следовательно, значение данной функции для произвольного  полностью определяется значениями в эквидистантных точках  на бесконечной оси азимутов, и может быть вычислено в соответствии с выражением [2-3]:

   , (1)

 

где  – функция, полученная бесконечным периодическим продолжением функции ;  – шаг дискретизации;  – число отсчетов интерполируемой функции на периоде, определенное в соответствии с теоремой отсчетов;  – остаток от целочисленного деления  на ; .

Сложность вычисления на практике значений интерполируемой функции в соответствии с выражением (1) связана с необходимостью суммирования бесконечного числа значений. При практической реализации вычислений ряд (1) обычно аппроксимируют суммой конечного числа слагаемых, что приводит к погрешности вычисления решающей функции. Данная погрешность называется ошибкой усечения [3]. В работе [4] оценивается погрешность аппроксимации правой части (1) в виде конечной суммы и отмечено, что ошибка усечения при интерполяции периодических функций не убывает с ростом числа используемых слагаемых правой части (1).

Цель настоящей работы – разработать подход, позволяющий с нулевой ошибкой усечения представлять 2π-периодические функции c финитным спектром Фурье в виде суммы конечного числа слагаемых.

Учитывая свойство 2π-периодичности исходной функции, правую часть можно переписать в следующем виде

                  ,                              (2)

 

где

.          (3)

 

Таким образом, бесконечную сумму (1) можно абсолютно точно представить в виде конечной суммы в соответствии с выражением (2) при условии получения замкнутых аналитических выражений для ядра данного разложения. Авторами настоящей работы были получено следующее замкнутое выражения ядра (3):

        .                   (4)

 

Ядро (4) представляет собой импульсную характеристику интерполирующего фильтра для интерполяции периодических функций с финитным спектром Фурье с высшей гармонической составляющей с номером  по последовательности отсчетов, состоящей из  эквидистантных отсчетов на период. Она периодична по переменной  с периодом . Комплексная частотная характеристика этого фильтра получается преобразованием Фурье импульсной характеристики и представляет собой отрезок ряда Фурье. Коэффициенты одностороннего комплексного ряда Фурье для ядра  имеют следующий вид:

                         –                                     (5)

для четного числа  отсчетов и

                         –                                     (6)

для нечетного .

С учетом (5)-(6) можно получить другое эквивалентное представление импульсной характеристики (4) для четного и нечетного числа отсчетов соответственно:

.           (7)

Непосредственно из (4) легко получить третье эквивалентное представление импульсной характеристики:

           .                      (8)

 

Однако рассмотрение спектра (5) импульсной характеристики фильтра для четных  показывает, что этот спектр избыточен, его составляющая с номером  является неинформативной. Если интерполируемая функция имеет спектральную составляющую с ненулевой амплитудой на частоте среза фильтра Котельникова, однозначное восстановление функции в общем случае невозможно, что иллюстрируется рис. 1. Здесь кружками, квадратами и треугольниками изображены отсчеты функции , взятые с начальной фазой 0, 15 и 45 градусов соответственно. Как видно из представленного графика, в зависимости от соотношения фаз импульсов дискретизации с частотой  и спектральной составляющей интерполируемой функции на частоте  амплитуды отсчетов могут изменяться от нуля до значения амплитуды рассматриваемой спектральной составляющей. При этом фаза «восстановленной» по таким отсчетам синусоиды может принимать значения в диапазоне от  до  относительно истинного значения. Это хорошо согласуется с тем фактом, что коэффициент передачи фильтра Котельникова как функция частоты, претерпевая разрыв на частоте среза, имеет на этой частоте значение 0,5 – среднее между значениями в полосе пропускания и в полосе задержки. То есть даже непрерывная синусоида с этой частотой проходит через фильтр с затуханием 6 дБ против 0 дБ в полосе пропускания. Более подробно данный вопрос исследован в работе [5].

 

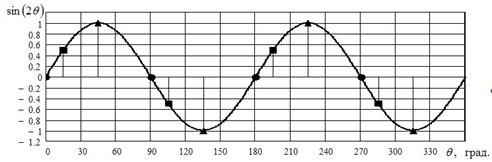
Рис.1 Отсчеты синусоиды с частотой

 

Для однозначного восстановления выборки сигнала, содержащей наивысшую гармонику порядка N, необходимо не менее  отсчетов. Таким образом, граница применимости теоремы отсчетов определяется строгим неравенством , хотя многие авторы, в том числе, в классических учебных пособиях (см, например, [6]) ошибочно определяют ее нестрогим неравенством . (Здесь  – частота наивысшей спектральной составляющей интерполируемой функции с ненулевой энергией, а  – частота дискретизации). Эта неопределенность обусловлена тем, что доказательство теоремы отсчетов Котельникова [2] базируется на интегральных преобразованиях Фурье функций с гладким спектром, а частный случай наличия в спектре интерполируемой функции дискретной спектральной составляющей на частоте , на которой коэффициент передачи фильтра Котельникова равен , отдельно не рассмотрен.

Целесообразно ввести понятие достаточного числа  отсчетов периодической функции с финитным спектром на период:

                                     ,                                                 (9)

где  – номер наивысшей гармоники в спектре интерполируемой функции.

Тогда для произвольного числа  эквидистантных отсчетов функции на периоде выражение (2) можно переписать в следующем виде:

.     

 

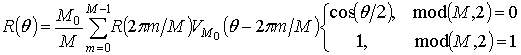При вычислении реакции интерполирующего фильтра в спектральной области произведение спектральных составляющих сигнала и импульсной характеристики фильтра с номером  должно быть равно нулю. Поэтому целесообразно для упрощения расчетов положить равной нулю соответствующую спектральную составляющую характеристики фильтра в правых частях (7)-(8).Тогда, выражения (4), (7) и (8) примут следующий вид:

         

             

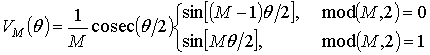
или

          ,                    (10)

где

      .                (11)

 

На рис. 2 в качестве иллюстрации приведены графики ядер разложения  и  на протяжении 3-х периодов интерполируемой функции по оси абсцисс. Для сравнения на том же рисунке приведены графики апериодического ядра Котельникова для той же частоты дискретизации .

 

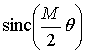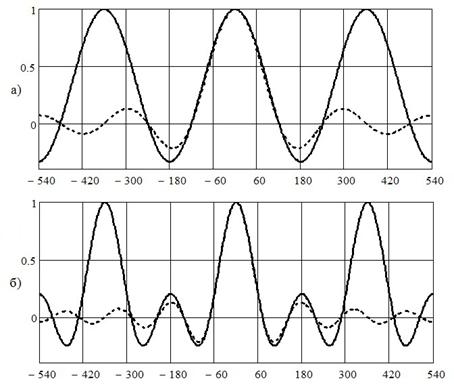
Рис.2 Графики функций  (а) и   (б)

 

Из выражения (10) видно, что ядро  является бесконечно дифференцируемой функцией. Следовательно, дифференцированием выражения (2) легко получить выражение для производной p-го порядка интерполируемой функции :

        .                 (12)

 

Правая часть выражения (2) представляют собой скалярное произведение

                                                                                 (13)

M-мерного вектора  отсчетов интерполируемой функции  и M-мерной вектор-функции  ядер разложения (2):

                  , ,

 – оператор транспонирования, , .                       

Аналогичным образом, производную (12) p-го порядка функции запишем как

                               ,                                         (14)

где  – производная p-го порядка вектор-функции .

С учетом того, что операция дифференцирования не создает новых спектральных составляющих, производная произвольного порядка от функции с финитным спектром имеет финитный спектр Фурье с тем же значением верхней частоты. Из этого следует, что если по формуле (12) вычислить вектор  значений производной -го порядка интерполируемой функции в точках ее отсчетов, то выражение для производной в произвольной точке можно записать в следующем виде:

                              ,                                       (15)

т.е. значение производной может быть вычислено в одном цикле со значением самой функции по формуле (13). Это позволяет сэкономить вычислительные ресурсы при выполнении повторяющихся вычислений, например, в итерационных процедурах оптимизации. Однако это правило следует с осторожностью применять к функциям «с практически финитным спектром», у которых энергия спектральных составляющих на частотах  пренебрежимо мала, но не равна нулю. Поскольку операция дифференцирования перераспределяет энергию процесса в сторону верхних частот, для обеспечения нужной точности вычислений по формуле (15) может потребоваться увеличение частоты дискретизации.

 

Выводы

Получено точное замкнутое представление 2π-периодической функции в виде конечной взвешенной суммы ее отсчетов на периоде с нулевой ошибкой усечения. Получено замкнутое выражение для ядра данного разложения, представляющего собой взвешенную сумму бесконечного числа ядер Котельникова. Показано, что ядро разложения является 2π-периодической функцией и достаточно просто выражается через значение аргумента интерполируемой функции и число ее отсчетов на периоде. Исследованы особенности поведения алгоритма интерполяции вблизи верхней частоты, равной половине частоты дискретизации. Полученные результаты носят общий характер и найдут свое практическое применение в различных областях науки и техники, в которых решается задача интерполяции периодических функций. В частности, предложенный подход позволяет представить диаграммы направленности произвольных антенных систем, измеренные с заданным шагом по аргументу, в виде аналитических функций.

 

Литература

1 Дмитриев И.С., Сличенко М.П. Максимально правдоподобное обнаружение и оценивание направления прихода и амплитуды напряженности радиоволны с помощью многоканального радиопеленгатора с антенной системой произвольной конфигурации. Антенны. 2011. Вып.5(168). С. 59-64.

2 Котельников В.А. О пропускной способности «эфира» и проволоки в электросвязи. М.: Физматлит, 2008. Собрание трудов. Т. 1. «Радиофизика. Информатика, телекоммуникации». С. 90-108.

3 Джерри. А. Дж. Теорема отсчетов Шеннона, ее различные обобщения и приложения. Обзор. ТИИЭР. 1977. Т.65. № 11. С. 53-89.

4 Хургин Я.И., Яковлев В.П. Финитные функции в физике и технике. М.: «Наука», 1971. – 408 с.

5 Харкевич А.А. Спектры и анализ. Изд. 3-е, перераб. М.: Гос. изд-во технико-теоретической литературы. 1957. – 238 с.

6 Баскаков С.И. Радиотехнические цепи и сигналы. Изд. 3-е, перераб. и доп. – М.: «Высшая школа», 2000. – 462 с.