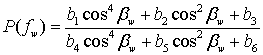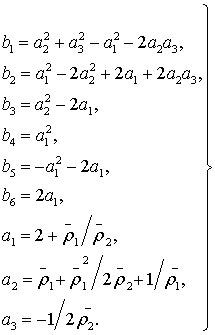УДК 621.372.832
ЧАСТОТНЫЕ СВОЙСТВА РЕАКТИВНЫХ СИММЕТРИЧНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ НА ОСНОВЕ ШЛЕЙФНЫХ СТРУКТУР
И. А. Петров
ФГУП «ЦНИРТИ им. академика А.И. Берга»
Статья получена 23 декабря 2013 г.
Аннотация. На основе теоремы о каскадном включении реактивных симметричных четырехполюсников проведен анализ частотных свойств шлейфных структур. Дана трактовка математической полосы пропускания реактивных симметричных четырехполюсников и ее отличие от физической полосы пропускания. На примере полосового фильтра с чебышевской характеристикой показано, что в физической полосе пропускания сложных четырехполюсников математическая полоса пропускания может иметь полосы заграждения, что приводит к увеличению уровня ослабления и коэффициента отражения при их каскадном включении.
Ключевые слова: теорема, устройства СВЧ; широкополосные согласующие структуры.
Abstract. The analysis of frequency characteristicы of shunting structures is carried out on the basis of the theorem about cascade connection of reactive symmetrical quadripoles. The Interpretation of mathematical passband is given for reactive symmetrical quadripoles and its change from physical passband is shown. By the example of the Chebyshev filter it is shown that in physical passband the complex quadripoles mathematical passband can have stopbands that brings to the increase of weakening level and reflection coefficient.
Keywords: theorem, microwave devices, broadband matching structures.
1. Теорема о каскадном включении одинаковых реактивных симметричных четырехполюсников.
В работах [1-9] приводятся многочисленные примеры проектирования устройств СВЧ с использованием широкополосных согласующих структур с короткозамкнутыми и разомкнутыми шлейфами. Совмещение подобных структур со структурами СВЧ устройств, синтезируемых общепринятыми методами, (так называемый, структурный синтез) позволяет: значительно увеличить число параметров для последующего параметрического синтеза, расширить рабочий диапазон частот, получить заданные амплитудно- и фазочастотные характеристики, значительно увеличить число вариантов схемотехнического построения устройств, в ряде случаев, придать результирующей структуре новые частотные свойства и функциональные возможности, уменьшить габариты разрабатываемых устройств и высокочастотных трактов.
Расчет устройств СВЧ является достаточно сложной задачей даже в приближении к теории цепей и длинных линий. Более точные решения могут быть получены на электродинамическом уровне при решении уравнений Максвелла с соответствующими начальными и граничными условиями. Однако, в этом случае сложность решаемых задач возрастает в значительной степени. Упрощение расчетов возможно, если выявлены общие закономерности структур, образующих устройства СВЧ и антенн. Теоремы позволяют не только выявить общие закономерности при анализе и синтезе устройств, но и дать более четкое физическое представление о взаимодействии базовых элементов, составляющих сложную электрическую цепь.
Применение, в качестве исходных широкополосных согласующих цепей каскадных соединений одинаковых реактивных симметричных четырехполюсников, обусловлено тем, что частотные свойства данных цепей (структур) определяются, прежде всего, параметрами элементов одиночного четырехполюсника. Данное свойство можно сформулировать в виде теоремы, которая приведена ниже.
Теорема: «При
каскадном включении одинаковых реактивных симметричных четырехполюсников
функция рабочего затухания результирующего четырехполюсника ![]() в математической полосе пропускания не
превышает значений функции
в математической полосе пропускания не
превышает значений функции ![]() , где
, где ![]() ,
, ![]() -
функция рабочего затухания одиночного четырехполюсника,
-
функция рабочего затухания одиночного четырехполюсника, ![]() -элемент
классической матрицы передачи одиночного четырехполюсника,
-элемент
классической матрицы передачи одиночного четырехполюсника, ![]() - частота в математической полосе
пропускания четырехполюсника».
- частота в математической полосе
пропускания четырехполюсника».
Результирующая функция рабочего
затухания каскадного соединения
![]() четырехполюсников
в полосе пропускания будет определяться следующим выражением
четырехполюсников
в полосе пропускания будет определяться следующим выражением
![]() ,
(1)
,
(1)
где
![]() - функция, определяемая только
параметрами одиночного четырехполюсника и равна
- функция, определяемая только
параметрами одиночного четырехполюсника и равна
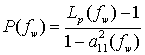 ,
(2)
,
(2)

- функция рабочего затухания одиночного четырехполюсника,
![]() .
.
В полосе пропускания
функция ![]() изменяется от 0 до 1 и результирующая функция рабочего
затухания (1) не превышает значений
изменяется от 0 до 1 и результирующая функция рабочего
затухания (1) не превышает значений ![]() . Под полосой пропускания, с
математической точки зрения, здесь понимаются частоты
. Под полосой пропускания, с
математической точки зрения, здесь понимаются частоты ![]() ,
на которых элемент
,
на которых элемент ![]() классической матрицы передачи
одиночного четырехполюсника лежит в пределах
классической матрицы передачи
одиночного четырехполюсника лежит в пределах
от -1 до 1, т.е. когда решение
разностных уравнений цепочки четырехполюсников [10] необходимо искать в виде ![]() . Таким образом, анализ частотных свойств
реактивных симметричных четырехполюсников, а также широкополосных согласующих
структур, получаемых при каскадном соединении подобных шлейфных
четырехполюсников, будем проводить на основе изложенной выше теоремы.
. Таким образом, анализ частотных свойств
реактивных симметричных четырехполюсников, а также широкополосных согласующих
структур, получаемых при каскадном соединении подобных шлейфных
четырехполюсников, будем проводить на основе изложенной выше теоремы.
2. Каскадные структуры с широкополосными короткозамкнутыми шлейфами.
Рассмотрим каскадные структуры, состоящие из четырехполюсников, представленных на рис. 1.
Рис. 1. Четырехполюсники с короткозамкнутыми шлейфами.
Первый четырехполюсник (рис.
1а) представляет собой последовательное соединение двух четвертьволновых
отрезков линий с волновым сопротивлением ![]() , между
которыми параллельно включен короткозамкнутый четвертьволновый шлейф с волновым
сопротивлением
, между
которыми параллельно включен короткозамкнутый четвертьволновый шлейф с волновым
сопротивлением ![]() . Элементы классической матрицы
передачи такого четырехполюсника определяются следующими выражениями:
. Элементы классической матрицы
передачи такого четырехполюсника определяются следующими выражениями:
 (3)
(3)
На основании выражений (2)
и (3) можно определить функцию ![]() , которая будет равна:
, которая будет равна:
где
На рис. 2 приведены
характеристики функций ![]() , выраженные в дБ, и
соответствующие значения КСВН для различных значений
, выраженные в дБ, и
соответствующие значения КСВН для различных значений ![]() и
и
![]() в зависимости от частотного параметра
в зависимости от частотного параметра ![]() .
.
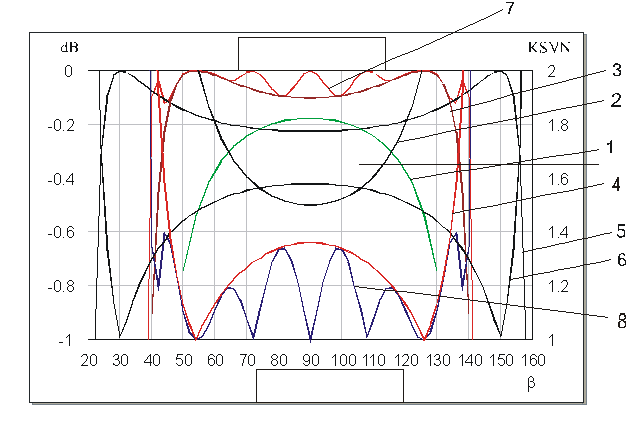
Рис. 2. Частотные характеристики функций ![]() и соответствующие значения КСВН.
и соответствующие значения КСВН.
При ![]() характеристики
имеют куполообразный характер и одну экстремальную в точке
характеристики
имеют куполообразный характер и одну экстремальную в точке ![]() . С уменьшением волновых сопротивлений
. С уменьшением волновых сопротивлений ![]() и
и ![]() значения
функции
значения
функции ![]() увеличиваются, характеристики расширяются
и при
увеличиваются, характеристики расширяются
и при ![]() 0,8165 в точке
0,8165 в точке ![]() равны
нулю. Дальнейшее уменьшение
равны
нулю. Дальнейшее уменьшение ![]() и
и ![]() приводит к появлению еще двух
экстремальных точек, равных 0, расположенных симметрично относительно точки
приводит к появлению еще двух
экстремальных точек, равных 0, расположенных симметрично относительно точки ![]() . На рис. 2 (кривые 3 и 4) приводятся
характеристики для значений
. На рис. 2 (кривые 3 и 4) приводятся
характеристики для значений ![]() 0,7. При
0,7. При ![]() <0,7 коэффициент перекрытия по
диапазону частот
<0,7 коэффициент перекрытия по
диапазону частот ![]() может быть равен 3 и более. На
рис. 2 (кривые 7 и 8) приводятся характеристики функции рабочего затухания
может быть равен 3 и более. На
рис. 2 (кривые 7 и 8) приводятся характеристики функции рабочего затухания ![]() в дБ и соответствующих значений КСВН для
структуры, состоящей из четырех четырехполюсников при
в дБ и соответствующих значений КСВН для
структуры, состоящей из четырех четырехполюсников при ![]() 0,7
и
0,7
и ![]() 4. Коэффициент перекрытия по диапазону
частот значительно возрастает, если выполняется соотношение
4. Коэффициент перекрытия по диапазону
частот значительно возрастает, если выполняется соотношение ![]() . На рис. 2 (кривые 5 и 6) приводятся
характеристики функции
. На рис. 2 (кривые 5 и 6) приводятся
характеристики функции ![]() и соответствующие значения КСВН
для:
и соответствующие значения КСВН
для: ![]() и
и ![]() , в
этом случая
, в
этом случая ![]() >6.
>6.
При разработке
широкополосных и сверхширокополосных устройств СВЧ, с использованием
рассматриваемой структуры, целесообразно, чтобы функция ![]() имела
три экстремальные точки, одну максимальную при
имела
три экстремальные точки, одну максимальную при ![]() и две
нулевые. Максимальное значение функции
и две
нулевые. Максимальное значение функции ![]() , тогда
принимая, что на границах полосы пропускания функция
, тогда
принимая, что на границах полосы пропускания функция ![]() ,
можно определить коэффициент перекрытия по диапазону частот
,
можно определить коэффициент перекрытия по диапазону частот ![]() , который будет равен
, который будет равен
![]() ,
, ![]() .
.
Значения ![]() определены
выражениями (5).
определены
выражениями (5).
В табл. 1 приведены
значения ![]() , соответствующее значение КСВН и
, соответствующее значение КСВН и ![]() для ряда значений
для ряда значений ![]() и
и
![]() .
.
Табл. 1. Расчетные значения КСВН и Кп для
различных значений ![]() и
и ![]() .
.
|
№ пп |
|
|
|
КСВН |
Кп |
|
1 |
0,8 |
0,8 |
-0,0018 |
1,042 |
1,63 |
|
2 |
0,75 |
0,75 |
-0,31 |
1,185 |
2,41 |
|
3 |
0,7 |
0,7 |
-0,102 |
1,36 |
2,9 |
|
4 |
0,65 |
0,65 |
-0,224 |
1,58 |
3,24 |
|
5 |
0,6 |
0,6 |
-0,406 |
1,85 |
3,5 |
|
6 |
0,55 |
0,55 |
-0,66 |
2,2 |
3,68 |
|
7 |
0,5 |
0,5 |
-1 |
2,67 |
3,82 |
|
8 |
0,85 |
2 |
-0,019 |
1,14 |
3,12 |
|
9 |
0,8 |
2 |
-0,075 |
1,3 |
4,15 |
|
10 |
0,7 |
2 |
-0,327 |
1,74 |
5,64 |
|
11 |
0,6 |
2 |
-0,82 |
2,42 |
6,81 |
|
12 |
0,85 |
3 |
-0,04 |
1,21 |
4,35 |
|
13 |
0,8 |
3 |
-0,111 |
1,32 |
5,44 |
|
14 |
0,7 |
3 |
-0,39 |
1,83 |
7,1 |
|
15 |
0,6 |
3 |
-0,9 |
2,53 |
8,47 |
Одиночный П - образный
четырехполюсник (рис. 1b) представляет собой последовательный четвертьволновый
отрезок линии передачи с волновым сопротивлением ![]() , по
краям которого включены параллельные короткозамкнутые четвертьволновые шлейфы с
волновым сопротивлением
, по
краям которого включены параллельные короткозамкнутые четвертьволновые шлейфы с
волновым сопротивлением ![]() . Элементы классической
матрицы передачи такого одиночного четырехполюсника будут равны
. Элементы классической
матрицы передачи такого одиночного четырехполюсника будут равны
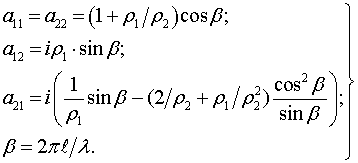 (7)
(7)
Функция ![]() и
и ![]() такого
четырехполюсника могут быть определены на оснований (4) и (6), но при этом
коэффициенты
такого
четырехполюсника могут быть определены на оснований (4) и (6), но при этом
коэффициенты ![]() …
…![]() будут
равны
будут
равны
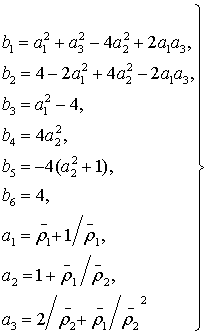 . (8)
. (8)
На центральной частоте
полосы пропускания ![]() и функция
и функция 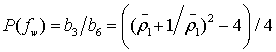 , т.е. зависит только от волнового
сопротивления последовательного отрезка линии, включенного между шлейфами. Для
, т.е. зависит только от волнового
сопротивления последовательного отрезка линии, включенного между шлейфами. Для ![]() на центральной частоте функция
на центральной частоте функция ![]() . При
. При ![]() значение
функции
значение
функции ![]() на центральной частоте увеличивается,
частотная характеристика функции
на центральной частоте увеличивается,
частотная характеристика функции ![]() имеет U – образный характер и этот случай не
имеет практического интереса. При
имеет U – образный характер и этот случай не
имеет практического интереса. При ![]() значение функции
значение функции ![]() на центральной частоте также
увеличивается, но в частотной характеристике функции
на центральной частоте также
увеличивается, но в частотной характеристике функции ![]() слева
и справа от центральной частоты появляются два нулевых минимума, полоса
пропускания расширяется.
слева
и справа от центральной частоты появляются два нулевых минимума, полоса
пропускания расширяется.
На рис. 3 (кривая 1)
приведена частотная характеристика КСВН для соответствующих значений функции ![]() четырехполюсника, изображенного на рис.
1б, при
четырехполюсника, изображенного на рис.
1б, при ![]() и
и ![]() Ом.
Там же приведены частотные характеристики КСВН этого четырехполюсника (кривая
2) и каскадного соединения 9 таких четырехполюсников (кривая 3). Необходимо
отметить, что при каскадном соединении подобных четырехполюсников проводимости
внутренних шлейфов в точках соединения будут складываться и их результирующее
волновое сопротивление равно
Ом.
Там же приведены частотные характеристики КСВН этого четырехполюсника (кривая
2) и каскадного соединения 9 таких четырехполюсников (кривая 3). Необходимо
отметить, что при каскадном соединении подобных четырехполюсников проводимости
внутренних шлейфов в точках соединения будут складываться и их результирующее
волновое сопротивление равно ![]() .
.
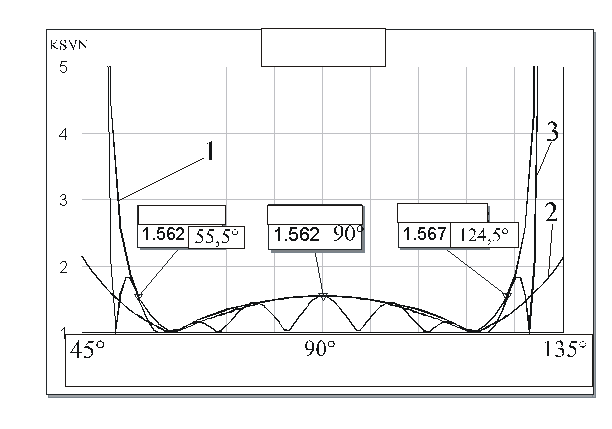
Рис. 3. Частотные характеристики КСВН П - четырехполюсников.
Как видно из рис. 3,
частотная характеристика функции ![]() П - образного
четырехполюсника по виду подобна Т – образному четырехполюснику. В табл. 2
приведены значения
П - образного
четырехполюсника по виду подобна Т – образному четырехполюснику. В табл. 2
приведены значения ![]() , соответствующее значение КСВН
и
, соответствующее значение КСВН
и ![]() для ряда значений
для ряда значений ![]() и
и
![]() П – образного четырехполюсника.
П – образного четырехполюсника.
Табл. 2. Расчетные значения КСВН и Кп для
различных значений ![]() и
и ![]() .
.
|
№ пп |
|
|
|
КСВН |
Кп |
|
1 |
0,9 |
1,8 |
-0,0488 |
1,235 |
1,89 |
|
2 |
0,8 |
1,6 |
-0,214 |
1,56 |
2,24 |
|
3 |
0,7 |
1,4 |
-0,541 |
2,04 |
2,46 |
|
4 |
0,8 |
0,8 |
-0,214 |
1,56 |
1,72 |
|
5 |
0,8 |
2,0 |
-0,214 |
1,56 |
2,47 |
|
6 |
0,8 |
4,0 |
-0,214 |
1,56 |
3,41 |
Сравнивая результаты анализа Т – и П
– образных четырехполюсников (например, п. 2 табл. 1 и соответствующий по
параметрам п. 4 табл. 2), можно сделать вывод, что коэффициент перекрытия
полосы пропускания Т – образных четырехполюсников примерно в 1,5 раза больше,
чем П – образных четырехполюсников. В данном сравнении учтено то, что максимуму
функций ![]() и соответствующие значения КСВН равны, а
волновые сопротивления внутренних шлейфов (кроме крайних) каскадного соединения
П – образных четырехполюсников уменьшаются в 2 раза и будут равны волновому
сопротивлению последовательных отрезков. Однако, при равенстве шлейфов,
структуры с П – образными четырехполюсниками имеют преимущество в том, что они
имеют меньшую длину.
и соответствующие значения КСВН равны, а
волновые сопротивления внутренних шлейфов (кроме крайних) каскадного соединения
П – образных четырехполюсников уменьшаются в 2 раза и будут равны волновому
сопротивлению последовательных отрезков. Однако, при равенстве шлейфов,
структуры с П – образными четырехполюсниками имеют преимущество в том, что они
имеют меньшую длину.
На рис. 1c приведен
четырехполюсник с тремя шлейфами. Его частотные характеристики и, в частности
характеристики функции ![]() , будут подобны четырехполюснику
на рис. 1b.
, будут подобны четырехполюснику
на рис. 1b.
Рассмотрим более интересный
случай, а именно четырехполюсник с 4 шлейфами, изображенный на рис. 1d. Его
волновые сопротивления ![]() ,
, ![]() ,
, ![]() и
и ![]() Ом
рассчитывались как полосовой фильтр с чебышевской характеристикой. Частотная
характеристика такого фильтра имеет равномерную пульсацию в физической полосе
пропускания и представлена на рис. 4 (кривая 1). Характеристики ослабления и
КСВН каскадного соединения четырех таких четырехполюсников приведены на рис. 4
(кривые 2).
Ом
рассчитывались как полосовой фильтр с чебышевской характеристикой. Частотная
характеристика такого фильтра имеет равномерную пульсацию в физической полосе
пропускания и представлена на рис. 4 (кривая 1). Характеристики ослабления и
КСВН каскадного соединения четырех таких четырехполюсников приведены на рис. 4
(кривые 2).
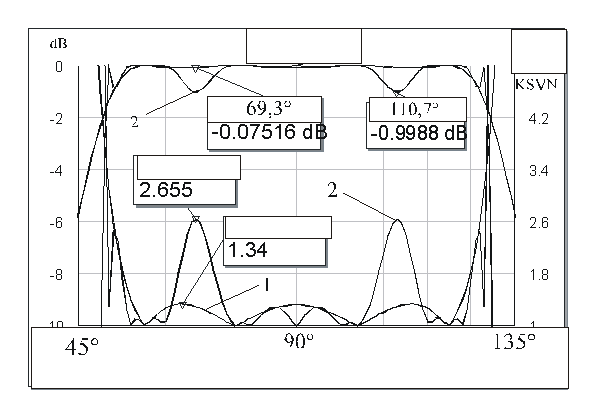
Рис. 4. Частотные характеристики 4-х шлейфного четырехполюсника.
Как видно, если для одиночного
четырехполюсника, представленного на рис. 1г, ослабление не превышает 0,08 дБ и
КСВН – 1,34, то для каскадного соединения четырех таких четырехполюсников,
ослабление увеличилось до 1 дБ, а КСВН до 2,7. Для объяснения этого факта
рассмотрим функцию ![]() , определяемую выражением (4).
Функция рабочего затухания
, определяемую выражением (4).
Функция рабочего затухания ![]() не превышает значения
1,01 (ослабление 0,08 дБ), следовательно числитель функции
не превышает значения
1,01 (ослабление 0,08 дБ), следовательно числитель функции ![]() близок к 0. Определим, как ведет себя
знаменатель.
близок к 0. Определим, как ведет себя
знаменатель.
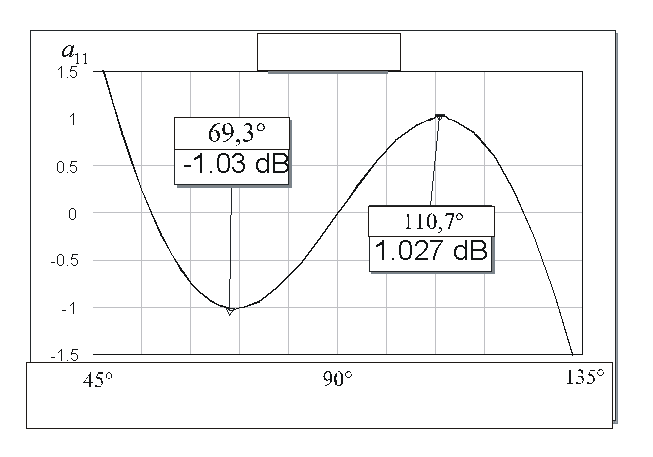
Рис. 5. Частотная зависимость элемента ![]() .
.
Элемент ![]() четырехполюсника на рис. 1d определяется
следующим выражением
четырехполюсника на рис. 1d определяется
следующим выражением
![]() (9)
(9)
где  ,
,
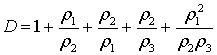 .
.
На рис. 5 приведена
частотная зависимость элемента ![]() , рассчитанная по
формулам (9). Как видно из приведенной зависимости, элемент
, рассчитанная по
формулам (9). Как видно из приведенной зависимости, элемент ![]() по абсолютной величине в диапазоне частот
принимает значения как больше, так и меньше 1.
по абсолютной величине в диапазоне частот
принимает значения как больше, так и меньше 1.
Элемент ![]() вблизи
вблизи ![]() =69,3°
(см. рис. 1.6) в двух точках принимает значение равное -1, следовательно
знаменатель функции
=69,3°
(см. рис. 1.6) в двух точках принимает значение равное -1, следовательно
знаменатель функции ![]() равен 0, а сама функция
стремится к
равен 0, а сама функция
стремится к ![]() . Между этими точками
. Между этими точками ![]() >1, функция
>1, функция ![]() не
существует, т.е. имеет разрыв. Вблизи
не
существует, т.е. имеет разрыв. Вблизи ![]() =110,7°
функция
=110,7°
функция ![]() также имеет разрыв. Следовательно, данный
четырехполюсник, рассчитанный как Чебышевский фильтр, в физической полосе
пропускания имеет «скрытые» математические полосы заграждение, которые
проявляются при каскадном соединении таких четырехполюсников. На рис. 6 приведена
частотная характеристика функция
также имеет разрыв. Следовательно, данный
четырехполюсник, рассчитанный как Чебышевский фильтр, в физической полосе
пропускания имеет «скрытые» математические полосы заграждение, которые
проявляются при каскадном соединении таких четырехполюсников. На рис. 6 приведена
частотная характеристика функция ![]() .
.
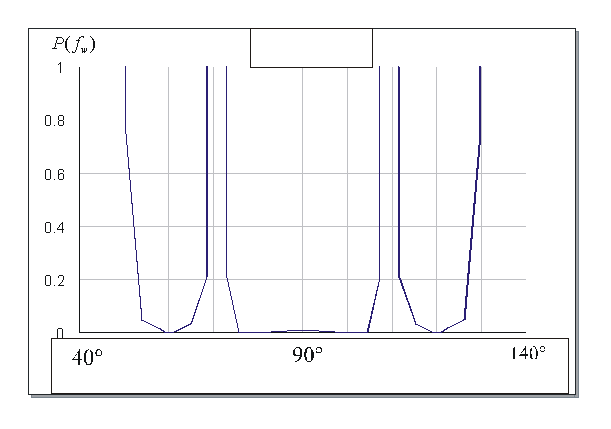
Рис. 6. Частотная характеристика функции ![]() 4-х
шлейфного четырехполюсника.
4-х
шлейфного четырехполюсника.
Естественно, изменяя
волновые сопротивления ![]() …
…![]() , можно
оптимизировать частотную характеристику с целью, чтобы функция
, можно
оптимизировать частотную характеристику с целью, чтобы функция ![]() не имела разрывов, не превышала
определенного значения, а элемент
не имела разрывов, не превышала
определенного значения, а элемент ![]() одиночного четырехполюсника
по абсолютной величине был менее 1 во всей физической полосе пропускания.
одиночного четырехполюсника
по абсолютной величине был менее 1 во всей физической полосе пропускания.
Четырехполюсники, у которых
в физической полосе пропускания функция ![]() не
имеет разрывов и не превышает определенного значения, а элемент
не
имеет разрывов и не превышает определенного значения, а элемент ![]() , будем называть четырехполюсниками с
оптимизированной функцией
, будем называть четырехполюсниками с
оптимизированной функцией ![]() .
.
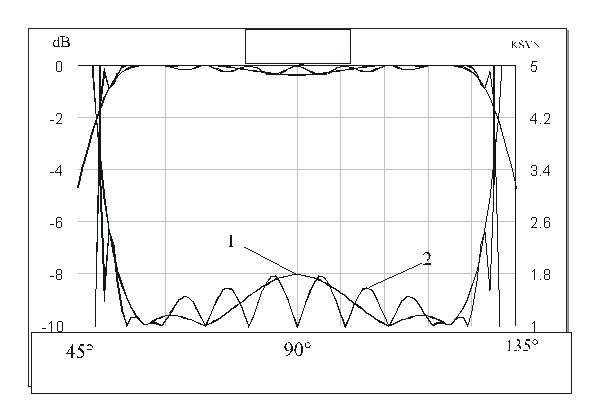
Рис. 7. Частотные характеристики 4-х шлейфного четырехполюсника.
Характеристики ослабления
и КСВН четырех шлейфного четырехполюсника с оптимизированной функцией ![]() и каскадного соединения четырех таких
четырехполюсников приведены на рис. 7 (кривые 1 и 2, соответственно). Волновые
сопротивления четырех шлейфного четырехполюсника после оптимизации имеют
следующие значения:
и каскадного соединения четырех таких
четырехполюсников приведены на рис. 7 (кривые 1 и 2, соответственно). Волновые
сопротивления четырех шлейфного четырехполюсника после оптимизации имеют
следующие значения: ![]() ,
, ![]() ,
, ![]() и
и ![]() Ом.
Частотные характеристики имеют не равномерную пульсацию и максимальное их
значение на центральной частоте.
Ом.
Частотные характеристики имеют не равномерную пульсацию и максимальное их
значение на центральной частоте.
Отметим, что при каскадном
соединении любого числа одинаковых четырехполюсников вида рис. 2а, 2b или 2c,
результирующий четырехполюсник будет иметь оптимизированную функцию ![]() .
.
3. Каскадные структуры с широкополосными разомкнутыми шлейфами.
Рассмотрим каскадную
структуру с Т - образными широкополосными шлейфами. Одиночный четырехполюсник
такой структуры представляет собой последовательное соединение двух отрезков
линий с волновым сопротивлением ![]() и длиной
и длиной ![]() , между которыми параллельно включен
разомкнутый шлейф с волновым сопротивлением
, между которыми параллельно включен
разомкнутый шлейф с волновым сопротивлением ![]() и
длиной
и
длиной ![]() . Элементов классической матрицы передачи
одиночного четырехполюсника равны:
. Элементов классической матрицы передачи
одиночного четырехполюсника равны:
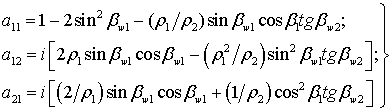 (10)
(10)
где, ![]() ,
, ![]() - частотные параметры.
- частотные параметры.
Используя выражения (4),
можно рассчитать функцию ![]() . На рис. 8 приведены характеристики
функции
. На рис. 8 приведены характеристики
функции ![]() и соответствующие значения КСВН в
зависимости от частотного параметра
и соответствующие значения КСВН в
зависимости от частотного параметра ![]() , а так же функция
, а так же функция ![]() при
при ![]() =10.
=10.
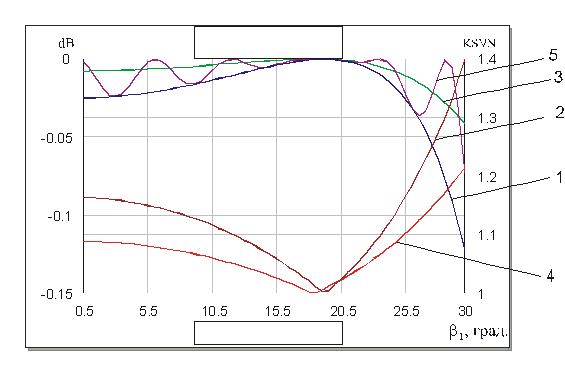
Рис. 8. Частотные характеристики функции ![]() .
.
Характеристики, приведенные
на рис. 8 показывают, что электрическую длину отрезка линии ![]() не следует выбирать более 25° для верхней
частоты рабочего диапазона устройства. Варьируя параметрами
не следует выбирать более 25° для верхней
частоты рабочего диапазона устройства. Варьируя параметрами ![]() ,
, ![]() ,
, ![]() ,
, ![]() , можно
получать структуры с любым максимальным значением коэффициента отражения в
заданной полосе рабочих частот.
, можно
получать структуры с любым максимальным значением коэффициента отражения в
заданной полосе рабочих частот.
Одиночный
четырехполюсник П - образной структуры представляет собой последовательный
отрезок линии с волновым сопротивлением ![]() и
электрической длиной
и
электрической длиной ![]() , по краям которого параллельно
включены разомкнутые шлейфы с волновым сопротивлением
, по краям которого параллельно
включены разомкнутые шлейфы с волновым сопротивлением ![]() и
электрической длиной
и
электрической длиной ![]() . Элементы классической матрицы
передачи можно определить на основании следующих выражений:
. Элементы классической матрицы
передачи можно определить на основании следующих выражений:
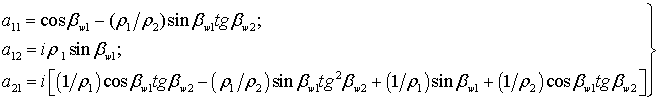 (11)
(11)
На основании выражений (4)
можно найти функцию ![]() , и определить частотные
свойства каскадного соединения подобных четырехполюсников.
, и определить частотные
свойства каскадного соединения подобных четырехполюсников.
На рис. 9 приведены частотные
характеристики КСВН Т – и П – образных одиночных четырехполюсников, а также их
каскадного соединения. На рис. 10 приведены характеристики разности фаз Т – и
П – образных одиночных четырехполюсников относительно фазовой длины отрезка
регулярной линии передачи. По оси абсцисс отложена электрическая длина
регулярной линии, изменяющаяся пропорционально частоте. Параметры элементов
одиночных четырехполюсников следующие: для Т – образного -![]() и
и ![]() Ом,
Ом, ![]() =12,2° и
=12,2° и ![]() =16,7°
на частоте 5 ГГц; для П– образного
=16,7°
на частоте 5 ГГц; для П– образного ![]() и
и ![]() Ом,
Ом, ![]() =20° и
=20° и ![]() =13,2° на частоте 5 ГГц.
=13,2° на частоте 5 ГГц.
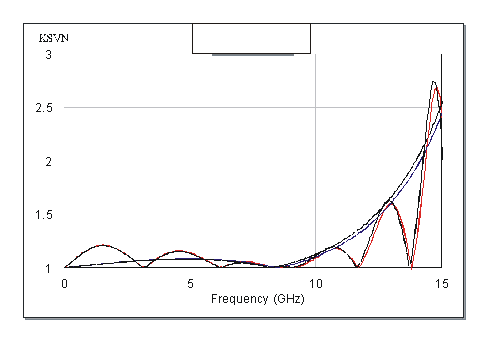
Рис. 9. Частотные характеристики Т – и П – образных четырехполюсников.
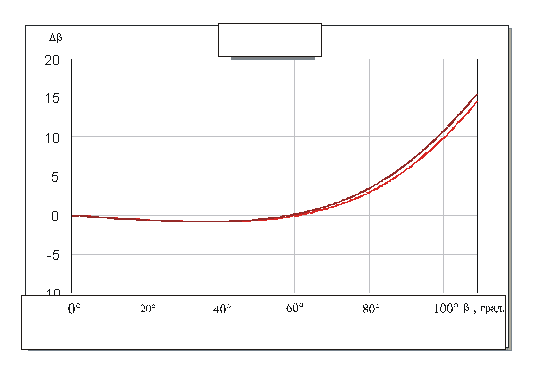
Рис. 10. Фазовые характеристики Т – и П – образных четырехполюсников.
Амплитудные и фазовые
характеристики Т – и П – образных одиночных четырехполюсников хорошо совпадают,
следовательно они тождественны. Фазовая длина Т – и П – образных одиночных
четырехполюсников по сравнению с регулярной линией увеличивается с ростом
частоты. Это связано с тем, что погонные емкости регулярной линии передачи
неизменны. В шлейфных четырехполюсниках входная проводимость разомкнутых
шлейфов, в точках подключения, равна  , т.е. не линейна.
Данное обстоятельство можно использовать для корректировки фазовых
характеристик в проектируемых устройствах. Отметим также, что при каскадном
включении П – образных четырехполюсников проводимости внутренних шлейфов (кроме
крайних) удваивается. Так для приведенных выше примеров, проводимости шлейфов
Т-образных четырехполюсников равны
, т.е. не линейна.
Данное обстоятельство можно использовать для корректировки фазовых
характеристик в проектируемых устройствах. Отметим также, что при каскадном
включении П – образных четырехполюсников проводимости внутренних шлейфов (кроме
крайних) удваивается. Так для приведенных выше примеров, проводимости шлейфов
Т-образных четырехполюсников равны ![]() , то проводимости
внутренних шлейфов каскадного соединения П – образных четырехполюсников равны
, то проводимости
внутренних шлейфов каскадного соединения П – образных четырехполюсников равны ![]() .
.
Структуры с разомкнутыми
шлейфами могут применяться для замены любого отрезка регулярной линии передачи
с любым волновым сопротивлением и с любой электрической длиной. Необходимую
электрическую длину и волновое сопротивление, рассмотренных выше структур,
синтезировать достаточно просто, меняя, например, только параметры отрезков ![]() и
и ![]() , а
волновые сопротивление соединительных отрезков задать, например, из конструктивных
и технологических соображений.
, а
волновые сопротивление соединительных отрезков задать, например, из конструктивных
и технологических соображений.
4. Комбинированные шлейфные структуры.
Широкополосные четырехполюсники с короткозамкнутыми и разомкнутыми шлейфами могут совмещаться между собой, в результате можно получать многочисленные варианты комбинированных шлейфных структур. На рис. 11 приведены три варианта комбинированных шлейфных структур.
На рис. 11а изображен Т – образный широкополосный четырехполюсник с короткозамкнутым шлейфом у которого все отрезки заменены широкополосными структурами с каскадным включением Т - образных разомкнутых шлейфов. На рис. 11б изображен П – образный широкополосный четырехполюсник с короткозамкнутыми шлейфами у которого последовательных отрезок заменен широкополосным четырехполюсником с Т - образным разомкнутым шлейфом. На рис. 11в изображен П – образный широкополосный четырехполюсник с короткозамкнутыми шлейфами у которого последовательных отрезок заменен широкополосным четырехполюсником с П - образными разомкнутыми шлейфами. Примеры применения комбинированных шлейфных структур приведены, например, работах [8, 9].
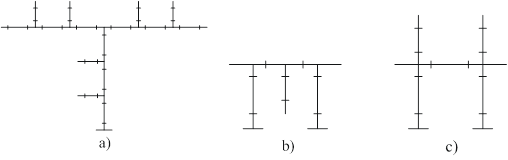
Рис. 11. Варианты четырехполюсников с комбинированными шлейфами.
Выводы:
1. На основе теоремы о каскадном включении реактивных симметричных четырехполюсников проанализированы свойства широкополосных структур с короткозамкнутыми и разомкнутыми шлейфами.
2. Дана трактовка математической полосы пропускания реактивных симметричных четырехполюсников и ее отличие от физической полосы пропускания.
3. На примере полосового фильтра с чебышевской характеристикой показано, что в физической полосе пропускания сложных четырехполюсников математическая полоса пропускания может иметь полосы заграждения, что приводит к увеличению уровня ослабления и коэффициента отражения при их каскадном включении.
Литература
1. Петров И.А. Многоканальный переключатель / Авторское свидетельство № 881902 H01P 1/15.. Приоритет от 06.09.1976. Опубликовано 15.11.1981, бюллетень № 42.
2. Петров И.А. Широкополосные согласующие структуры и их применение в устройствах СВЧ. // Физика волновых процессов и радиотехнические системы. 2010. Т. 13. № 2. С. 52-57.
3. Петров И.А. Проектирование устройств СВЧ путем совмещения их с широкополосными согласующими структурами. Сборник научных трудов ЦНИРТИ им. академика А.И. Берга. Под редакцией Б.С. Лобанова. М: ООО НИЦ «Инженер». 2011. Т.5, Ч.2. С. 34-61.
4. Неганов В.А., Петров И.А. Структурный синтез сверхширокополосных делителей мощности СВЧ. // Тезисы докладов и сообщений Х Международной научно-технической конференции «Физика и технические приложения волновых процессов», 11-17 сентября 2011 г. Самара. С. 97-98.
5. Лобанов Б.С., Петров И.А. Делители мощности СВЧ с заданными фазо-частотными характеристиками. // Тезисы докладов и сообщений Х Международной научно-технической конференции «Физика и технические приложения волновых процессов», Самара 2011 г. С. 98-100.
6. Петров И.А. Многоканальные СВЧ переключатели с полупроводниковыми элементами на основе широкополосных согласующих структур. // Физика волновых процессов и радиотехнические системы. 2011. Т. 14 . № 4. С. 60-66.
7. Петров И.А. Фильтры СВЧ с использованием широкополосных согласующих структур. // Физика волновых процессов и радиотехнические системы. 2011. Т. 14 . № 1. С. 51-56.
8. Петров И.А. Структурный синтез линейных и нелинейных СВЧ устройств с использованием широкополосных согласующих структур. // Кандидатская диссертация. Самара, 2011. - 133с. Поволжский государственный университет телекоммуникации и информатики. Научный руководитель д.ф-м.н., профессор В.А. Неганов, консультант, д.т.н. Б.С. Лобанов.
9. Петров И.А. Частотные свойства реактивных симметричных четырехполюсников на основе шлейфных структур. // I Всероссийская Микроволновая конференция. Доклады. Москва, ИРЭ им. В.А. Котельникова РАН. 2013. С. 366-369.
10. Фельдштейн А.Л., Явич Л.Р. Синтез четырехполюсников и восьмиполюсников на СВЧ (второе издание). - М.: Связь, 1971. – 388с.