УДК 621.396.677
ОПТИМИЗАЦИЯ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК АНТЕННОЙ РЕШЕТКИ С УЧЕТОМ ФЛУКТУАЦИЙ АМПЛИТУДНО-ФАЗОВОГО РАСПРЕДЕЛЕНИЯ И ОТКАЗОВ ОТДЕЛЬНЫХ ЭЛЕМЕНТОВ
С. Е. Мищенко, Н. В. Шацкий
Научно-исследовательский институт физики Южного федерального университета
Статья получена 20 декабря 2013 г.
Аннотация. Рассматривается задача максимизации отношения сигнал/помеха антенной решетки с отказами элементов и флуктуациями амплитудно-фазового распределения. Получено выражение для средней диаграммы направленности антенной решетки с учетом флуктуаций амплитудно-фазового распределения и отказов. Показано, что задача энергетической оптимизации с использованием полученного выражения не может быть решена с использованием методов матричного синтеза. Предложено использовать градиентный метод оптимизации. В ходе численных исследований установлено, что использование предлагаемого подхода позволяет стабилизировать, глубину формируемого «нуля» диаграммы направленности в направлении на источник помех.
Ключевые слова: антенная решетка, энергетическая оптимизация, амплитудно-фазовое распределение, отказ элемента, флуктуации.
Abstract. The problem of maximizing the signal / noise ratio of the antenna array elements with failures and fluctuations in the amplitude and phase distribution is considered. An expression for the average of the antenna array with fluctuations amplitude-phase distribution is obtained. It is shown that the problem of energy optimization using the resulting expression can not be solved using methods of matrix synthesis . We propose to use a gradient optimization method . During numerical studies it was found that the use of the proposed approach allows to stabilize the depth of the formed "zero" radiation pattern in the direction to the source of interference.
Key words: antenna array, energy optimization, amplitude and phase distribution, element failure, fluctuations.
Введение
Существующая статистическая теория антенн [1,2] позволяет при решении задач синтеза определять статистические характеристики направленности антенн с учетом флуктуаций амплитудно-фазового распределения (АФР) и координат излучателей. Использование данного подхода позволяет моделировать характеристики направленности реальных антенных систем с учетом отказов элементов или их конструктивных особенностей. Например, в приемной цифровой антенной решетке (АР) или передающей активной АР отказы малошумящих усилителей в отдельных каналах могут моделироваться путем уменьшения амплитуд комплексных весовых коэффициентов по сравнению с заданными. В передающих трактах флуктуации фазы могут увязываться с ошибками калибровки, дискретностью управления, а флуктуации амплитуд − с паразитной модуляцией коэффициента передачи фазовращателя при переключении ступеней дискретного фазовращателя. Использование адекватных моделей АР позволяет получать обоснованные технические решения при проектировании антенных систем. Для этого необходимо решать задачи синтеза АР с учетом флуктуаций амплитудно-фазового распределения и отказов элементов.
Целью работы является разработка метода оптимизации отношения сигнал/помеха цифровой антенной решетки с учетом флуктуаций амплитудного распределения и отказов отдельных элементов.
1 Математическая модель антенной решетки
Рассмотрим ![]() -элементную цифровую АР, ДН излучателей
которой описываются комплексными функциями
-элементную цифровую АР, ДН излучателей
которой описываются комплексными функциями ![]()
![]() .
.
ДН идеальной АР описывается выражением вида:
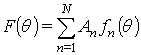 , (1)
, (1)
где ![]() −
комплексный весовой коэффициент
−
комплексный весовой коэффициент ![]() -го канала АР.
-го канала АР.
При наличии флуктуаций амплитудного распределения вектор амплитудно-фазового распределения может быть представлен в виде суммы регулярной части и случайной ошибки с одинаковыми фазами [1,2]:
![]() . (2)
. (2)
При малых фазовых ошибках, ограничиваясь только линейными членами разложения последней экспоненты в ряд, имеем:
![]() .(3)
.(3)
Учитывая порядок малости
случайной величины ![]() , выражение (3) можно упростить
к виду:
, выражение (3) можно упростить
к виду:
![]() . (4)
. (4)
Флуктуации амплитуд и фаз
могут отражать разброс параметров диаграммообразующей схемы, включающей в
каждом канале, малошумящий усилитель, преобразователь частоты и ![]() -разрядный АЦП [3], а также неточность
значений амплитуд и фаз комплексных отсчетов сигналов при преобразовании
аналог-цифра.
-разрядный АЦП [3], а также неточность
значений амплитуд и фаз комплексных отсчетов сигналов при преобразовании
аналог-цифра.
Пусть в составе решетки
имеются элементы с отказами, образующие множество ![]() . При
этом будет наблюдаться уменьшение амплитуды комплексного коэффициента передачи
канала.
. При
этом будет наблюдаться уменьшение амплитуды комплексного коэффициента передачи
канала.
Тогда ДН АР с отказами может быть представлена в виде:
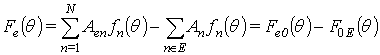 . (5)
. (5)
Представление результирующей ДН в виде разности (5) позволяет смоделировать ситуацию, при которой неисправные каналы являются источниками шума.
Найдем ДН АР по мощности:
![]() (6)
(6)
где символ «*» обозначает операцию комплексного сопряжения.
После большого количества
реализаций АФР с флуктуациями значений комплексных весовых коэффициентов
получим среднюю ДН АР по мощности ![]() , выражение для которой
на основании (5) составляют слагаемые:
, выражение для которой
на основании (5) составляют слагаемые:
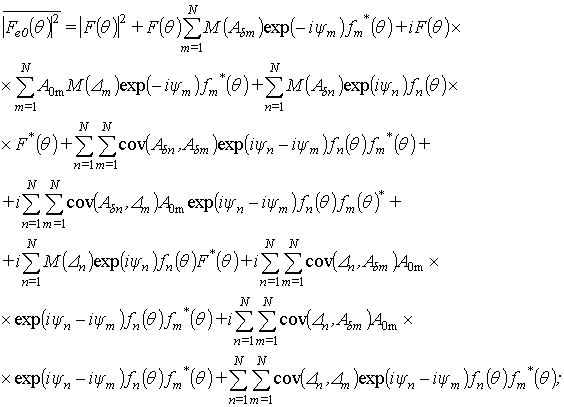 (7)
(7)
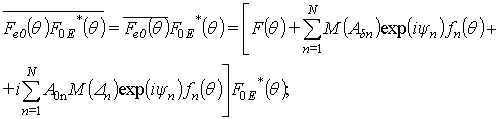 (8)
(8)
![]() ; (9)
; (9)
![]() ,
(10)
,
(10)
где ![]() обозначает
математическое ожидание случайной величины
обозначает
математическое ожидание случайной величины ![]() ;
; ![]() − ковариация случайных величин
− ковариация случайных величин ![]() и
и ![]() .
.
Здесь и в дальнейшем черта над функцией обозначает усреднение по множеству амплитудно-фазовых распределений со случайными ошибками амплитуд и фаз комплексных весовых коэффициентов.
Если допустить, что
ошибки различных типов и ошибки в каналах являются независимыми, а
математические ожидания ошибок ![]() и
и ![]() равны нулю, то выражения (7)-(9) существенно
упрощаются:
равны нулю, то выражения (7)-(9) существенно
упрощаются:
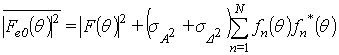 ;
(11)
;
(11)
![]() ,
(12)
,
(12)
где ![]() и
и ![]() − дисперсии амплитудных и фазовых
ошибок соответственно.
− дисперсии амплитудных и фазовых
ошибок соответственно.
С учетом полученных выражений имеем:
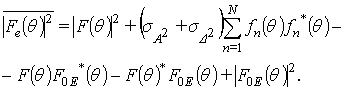 (13)
(13)
Выполним теперь
усреднение ДН по различным реализациям отказов элементов в составе АР. Для
этого введем параметр ![]() , характеризующий частоту выхода
из строя
, характеризующий частоту выхода
из строя ![]() -го элемента в статистической выборке:
-го элемента в статистической выборке:
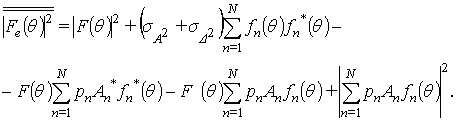 (14)
(14)
Здесь и в дальнейшем двойная черта над функцией обозначает операцию усреднения ДН по множеству реализаций различных конфигураций АР с отказами элементов и флуктуаций амплитудно-фазового распределения.
2 Метод энергетической оптимизации антенной решетки
Рассмотрим теперь задачу амплитудно-фазового синтеза нулей рассматриваемой АР в следующей постановке
Пусть задано
пространственное распределение мощности помех, описываемое функцией ![]() . Требуется найти комплексные весовые
коэффициенты
. Требуется найти комплексные весовые
коэффициенты ![]() , обеспечивающие максимизацию отношения
сигнал/шум, описываемое функционалом вида:
, обеспечивающие максимизацию отношения
сигнал/шум, описываемое функционалом вида:
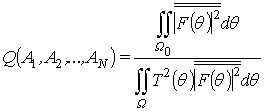 ,
(15)
,
(15)
где ![]() −
область углов, в которой расположен источник сигнала;
−
область углов, в которой расположен источник сигнала; ![]() −
область углов, в которой заданы источники помех.
−
область углов, в которой заданы источники помех.
Обычно для решения данной задачи используется матричный синтез [4,5], применимость которого определяется возможностью представления функционала (15) в виде отношения эрмитовых форм. Однако, при рассмотрении АР с отказами матричный синтез не может быть применен, что обусловлено тем, что третье и четвертое слагаемое в выражении (14), а также их сумма не могут быть представлены в виде эрмитовой формы.
В связи с этим для
решения сформулированной задачи воспользуемся классическим градиентным подходом
[6], в соответствии с которым поиск решения осуществляется в ходе итерационного
процесса. На шаге ![]() амплитудно-фазовое
распределение определяется путем смещения начального решения в сторону
градиента функционала (15) по формуле:
амплитудно-фазовое
распределение определяется путем смещения начального решения в сторону
градиента функционала (15) по формуле:
![]() ,
(16)
,
(16)
где ![]() −
заданная скорость приближения к экстремуму;
−
заданная скорость приближения к экстремуму; ![]() ;
;
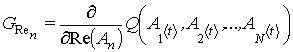 ;
(17)
;
(17)
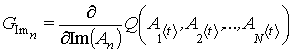 (18)
(18)
− действительная и мнимая части компонентов градиента функционала (15).
Если
![]() ,
,
то происходит дробление параметра ![]() и возвращение к предыдущим значениям
комплексных весовых коэффициентов. В частности [4, 6], один из возможных
вариантов состоит в том, что
и возвращение к предыдущим значениям
комплексных весовых коэффициентов. В частности [4, 6], один из возможных
вариантов состоит в том, что
![]() .
(19)
.
(19)
После этого осуществляется переход к следующему шагу итерационного процесса.
3 Численные исследования
Рассмотрим ![]() -элементную линейную эквидистантную АР
излучателей, комплексные ДН которых описываются функциями вида:
-элементную линейную эквидистантную АР
излучателей, комплексные ДН которых описываются функциями вида:
![]() ,
(20)
,
(20)
где ![]() −
координата
−
координата ![]() -го элемента АР;
-го элемента АР; ![]() −
шаг решетки.
−
шаг решетки.
Распределение вероятностей выхода из строя элементов АР было задано случайным образом. Вероятность выхода из строя каждого элемента изменялась в диапазоне от 0 до 0,75.
На рис. 1 приведено сгенерированное распределение вероятностей:
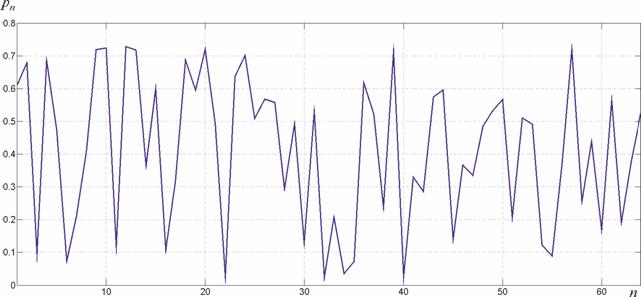
Рис. 1 − Распределение частот выхода из строя по элементам АР
Пусть необходимо снизить
уровень боковых лепестков в направлении ![]() (первый
боковой лепесток ДН с равномерным возбуждением).
(первый
боковой лепесток ДН с равномерным возбуждением).
На рис. 2 приведены средняя ДН АР с амплитудно-фазовым распределением, синтезированным с учетом статистики отказов антенных элементов (красная кривая) и одна из частных реализаций ДН, с использованием данного АФР при выходе из строя 9, 10, 12, 13, 20, 24, 39, 57-го элементов (зеленая кривая). Синим цветом показана ДН, полученная при использовании амплитудного распределения, найденного матричным методом в случае отказа перечисленных элементов. Наличие отказов приводит к уменьшению глубины формируемого «нуля» ДН. Так, в результате решения задачи энергетической оптимизации АР с отказами в направлении нуля был сформирован уровень −49,9 дБ. При выходе из строя указанных излучателей в направлении на источник помех УБЛ составляет −37,4 дБ. Для красной кривой этот уровень составил −25,7 дБ.
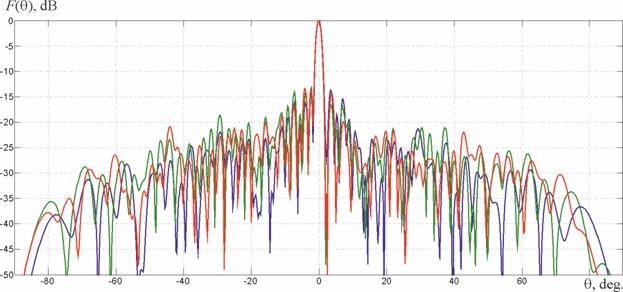
Рис. 2 − ДН АР после энергетической оптимизации
(красная кривая) и
для АР с отказами при использовании различных распределений
(зеленая кривая − синтез с отказами, синяя синтез идеальной АР при
наличии отказов)
Проведенные исследования показали, что формирование средней ДН с пониженным УБЛ в заданном направлении позволяет стабилизировать уровень боковых лепестков в условиях отказов, но зависит от имеющейся статистики отказов.
На рис. 3 и 4 представлены амплитуды и фазы комплексных весовых коэффициентов при решении задачи синтеза «нуля» матричным методом (красная кривая) и с использованием предлагаемого подхода (синяя кривая) соответственно. Изрезанная форма амплитудного и фазового распределения связана с заданной статистикой отказов и объясняется тем, что в формирование ДН АР увеличивается вклад тех элементов, вероятность отказов которых ниже.
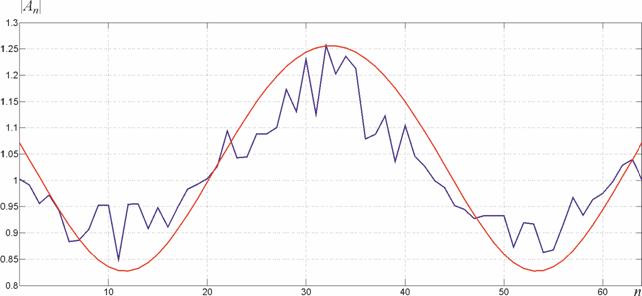
Рис. 3 − Синтезированное амплитудное
распределение , полученные матричным методом
в идеальной АР (красная кривая) и
предлагаемым методом (синяя кривая)
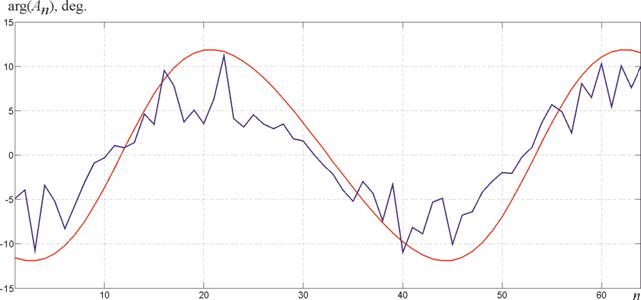
Рис. 4 − Синтезированные фазовые распределения в
АР, полученные матричным методом
в идеальной АР (красная кривая) и предлагаемым
методом (синяя кривая)
Выводы
Таким образом, предложена модель АР, позволяющая учесть влияние флуктуаций амплитудно-фазового распределения и отказов отдельных элементов на форму средней ДН по мощности. Сформулирована задача амплитудно-фазового синтеза нулей АР, для которой имеется статистика отказов элементов. Показано, что при формировании «нулей» средней ДН матричные методы синтеза не могут быть использованы, что приводит к необходимости решать оптимизационную задачу другими методами. Использование предлагаемого подхода позволяет стабилизировать характеристики направленности антенны, в частности, глубину формируемого «нуля» ДН при условии выхода из строя элементов за счет увеличения вклада наиболее работоспособных элементов в формирование ДН.
1 Шифрин Я.С. Вопросы статистической теории антенн. − М.: Сов радио, 1970, 384с.
2 Проблемы антенной техники/ Под ред. Бахраха Л.Д., Воскресенского Д.И. М.: Радио и связь, 1989, 368с.
3 Задорожный В.В., Ларин А.Ю., Оводов О.В., Христианов В.Д. Оптимизация приемных цифровых антенных решеток // Антенны, 2012, Вып. 9(184), С. 24-31.
4 Зелкин Е.Г., Соколов В.Г. Методы синтеза антенн: Фазированные антенные решетки и антенны с непрерывным раскрывом. - М.: Сов. радио, 1980. 290с.
5 Cheng David. K. Optimization techniques for antenna array// IEEE Proc. 1971. V.59. № 12. Р.1664-1674.
6 Шуп Т. Решение инженерных задач на ЭВМ// Практическое руководство / Пер. c англ. - М.: Мир, 1982.