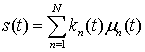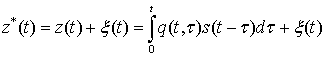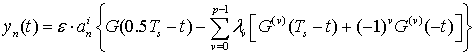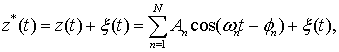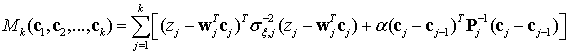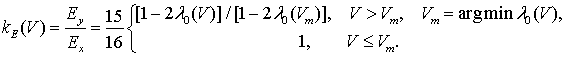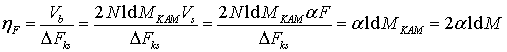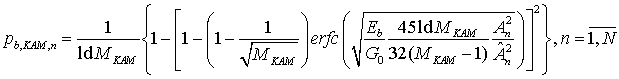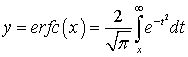ИНТЕЛЛЕКТУАЛЬНЫЙ МОДЕМ НА ОСНОВЕ МНОГОЧАСТОТНОЙ МОДУЛЯЦИИ

В. Г. Санников

Московский технический университет связи и информатики

Статья получена 29 декабря 2014 г.

Аннотация. В работе предлагается метод передачи дискретных сообщений на основе интеллектуального модема с многочастотной модуляцией. Оптимизация модема осуществляется на основе синтеза оптимальных финитных сигналов в индивидуальных каналах, не вызывающих межсимвольных искажений и обеспечивающих максимальное значение отношения сигнал/шум на входах согласованных фильтров демодулятора. Оценка параметров модема с целью выравнивания характеристик частотно-ограниченного канала связи осуществляется на основе метода оптимальной рекуррентной фильтрации. Дан теоретической анализ эффективности и помехоустойчивости модема. Основные результаты статьи докладывались и обсуждались на VII Всероссийской конференции «Радиолокация и радиосвязь», 24-26 ноября 2014 г.

Ключевые слова: система передача данных, интеллектуальный модем, многочастотный метод модуляции, оптимальные финитные сигналы, эффективность, помехоустойчивость.

Abstract. The method of transmission of the discrete messages on the basis of the intellectual modem with multifrequency modulation in-process is offered. Modem optimization is carried out on the basis of synthesis of optimum finite signals in the individual channels not calling the intersymbol distortions and ensuring maximum value of a signal/noise ratio on entries of matched filters of the demodulator. The estimation of parameters of the modem for the purpose of smoothing of performances of the is frequency-limited communication channel is carried out on the basis of a method of an optimum recurrent filtering. The analysis of effectiveness and a noise stability of the modem is given theoretical.

Keywords: system a data transmission, the intellectual modem, a multifrequency method of modulation, optimum finite signals, effectiveness, a noise stability.

1. Введение

В телекоммуникационной практике при передаче дискретных сообщений (ДС) по частотно-ограниченным каналам связи (КС), с целью нивелирования межсимвольных искажений (МСИ), широко применяется метод параллельной многочастотной модуляции (МЧМ), в англоязычной литературе это метод DMT (Discrete Multi None) [1-3]. Здесь для передачи ДС используется ряд параллельных индивидуальных каналов с центральными частотами , спектры сигналов в которых занимают полосу частот , много меньшую полосы частот канала связи (см. рис. 1). По сравнению с методом последовательной одночастотной передачи этот метод имеет то преимущество, что практически не чувствителен к искажениям амплитудно-частотных (АЧХ) и фазо-частотных (ФЧХ) характеристик КС и, как следствие, приводит к значительному упрощению задачи выравнивания на приеме передаточной функции КС.

Важное свойство модемов с МЧМ, заключающееся в слабой зависимости качества передачи ДС от искажений АЧХ и ФЧХ КС, обеспечило им широкое распространение в радиоканалах с многолучевым распространением и значительными селективными частотными искажениями. Известны различные модификации такого вида модемов, отличающиеся формой спектров сигналов-переносчиков, а также частотными характеристиками соответствующих приемных фильтров [1-3].

Рис. 1 – Размещение индивидуальных подканалов в частотно-ограниченном КС при МЧМ

Отличительной особенностью предлагаемого модема является использование в его индивидуальных подканалах полосовых фильтров, низкочастотным эквивалентом (НЧЭ) которых является формирующий фильтр (ФФ) Баттерворта (рис. 1), для которого синтезируются оптимальные финитные сигналы (ОФС), принципиально не вызывающие МСИ на его выходе [4-6]. При определении полосы частот подканалов, обеспечивающих заданный уровень ослабления АЧХ, ОФС обеспечивают минимальный уровень межканальных искажений.

2. Функциональная схема и принцип действия интеллектуального модема

Функциональная схема многочастотного модема приведена на рисунке 2 [5].

Рис. 2 – Функциональная схема интеллектуального модема с МЧМ

Данный модем относится к классу интеллектуальных модемов [2], так как оптимизация его характеристик осуществляется как на приемном, так и на передающем концах системы передачи ДС. В схеме модема (рис. 2) введены обозначения: ФС – формирователь ОФС, ФВ – фазовращатель на , БВС – блок вхождения в связь, БОП КПС – блок оценки параметров канала прямой связи, СФ – согласованный фильтр, СВТЧ – схема восстановления тактовой частоты, МПРУ – многопороговое решающее устройство.

В модуляторе двоичное сообщение с длительностью бита , представляющее собой «быстрый» поток прямоугольных импульсов разной полярности (), в демультиплексоре преобразуется в «медленных» импульсных потоков , с длительностью импульсов . Пример такого преобразования при показан на рисунке 3.

Рис. 3 – Сигналы на входе и выходе демультиплексора модема с МЧМ (N=3)

В блоке цифровой поток -ого индивидуального канала разбивается на два подканала:

· синфазный (ось ) со значениями , где 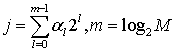, - двоичный эквивалент целого числа , - энергетическая база сигнала - ичной амплитудной манипуляции (АМ);

· квадратурный (ось ) со значениями , , 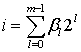- двоичный эквивалент целого числа .

На выходе -ого индивидуального канала на длительности символа

, (1)

формируется сигнал квадратурной АМ (КАМ)

, (2)

где - оптимальные финитные сигналы (ОФС), формируемые в блоках ФС (рис. 2), , - гармонические колебания, наблюдаемые на выходе генератора сетки частот, - гармонические колебания, наблюдаемые на выходах фазовращателей (ФВ) на , - двоичный логарифм, .

Отклик модулятора наблюдается на выходе сумматора и, соответственно, равен

, (3)

где - регулируемые коэффициенты передачи индивидуальных каналов модема.

На вход демодулятора модема с выхода шумового КС поступает сигнал вида

, (4)

где - импульсная реакция, связанная с комплексным коэффициентом передачи КС посредством преобразования Фурье, - аддитивный белый гауссовский шум (АБГШ).

Сигнал одновременно поступает на вход блока оценки параметров КС (БОП КПС) и входы индивидуальных квадратурных подканалов, содержащих перемножителей сигнала с опорными синфазными , колебаниями, формируемых на выходах генератора сетки частот демодулятора, и квадратурными колебаниями на выходах ФВ. Сигналы с выходов перемножителей поступают на фильтры (СФ) индивидуальных подканалов, согласованные с ОФС . Отклики СФ в моменты, кратные , поступают на блоки МПРУ, на выходах которых образуются оценки сигналов КАМ. На выходах блоков восстанавливаются «медленные» импульсные потоки индивидуальных подканалов , которые на выходе мультиплексора объединяются в «быстрый» импульсный поток , представляющий собой оценку переданного ДС .

В виду того, что возникает актуальная задача оптимизации работы модема, в результате решения которой обеспечивается минимизация вероятности ошибочных решений в МПРУ. Основными блоками, требующими оптимизации, являются блоки ФС формирования оптимальных финитных сигналов модулятора и блок оценки параметров КС (БОП КПС) демодулятора (рис. 2). Перейдем к их рассмотрению.

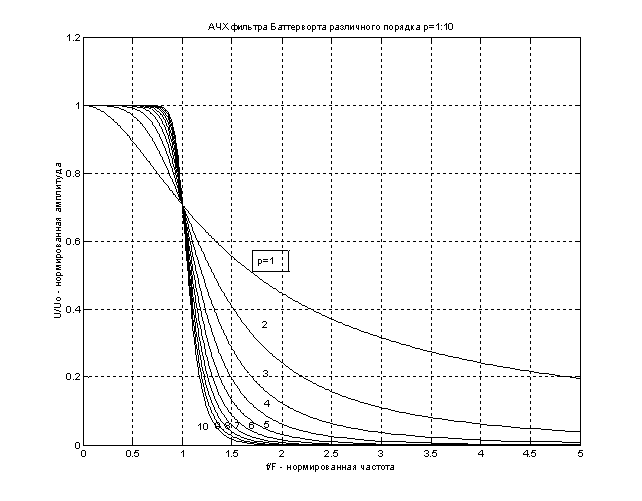
3. Метод формирования оптимальных финитных сигналов

В качестве низкочастотного эквивалента (НЧЭ) для фильтров индивидуальных каналов многочастотного модема (рис. 1) часто используют фильтр Баттерворта порядка , АЧХ которого: , приведена на рисунке 4.

Рис. 4 – Амплитудно-частотные характеристики фильтра Баттерворта

Оптимальные финитные сигналы (ОФС) модулятора одинаковы для всех каналов и синтезируются на основе фильтра Баттерворта по критерию максимума отношения сигнал/шум (ОСШ) в середине посылки длительностью на входе согласованного фильтра (СФ) демодулятора, в соответствие с соотношением [4]:

, (5)

где , - энергия ОФС на входе НЧЭ фильтра Баттерворта.

В (5) - канальная функция определяется по следующему соотношению [4,5]:

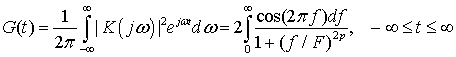На основе табличного интеграла [6], и последующего дифференцирования, канальная функция (v = 0) и её производные (v > 0) в (5) для фильтра Баттерворта порядка с граничной частотой , соответственно равны [4,5]:

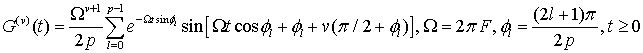(6)

с учетом следующего свойства: .

В (5) - множители Лагранжа решения вариационной задачи синтеза ОФС, определяемые из системы уравнений вида [5]:

, (7)

где , .

Временное и спектральное представления ОФС рассмотрены в работах [5,7].

4. Метод оценки параметров канала связи на основе полигармонической фильтрации

В современных интеллектуальных модемах для уменьшения межсимвольных искажений, возникающих из-за ограничения полосы частот индивидуальных каналов и приводящих к снижению помехоустойчивости системы передачи дискретных сообщений, часто используют выравниватели АЧХ и ФЧХ каналов связи (эквалайзеры) на приёме [1-3]. Это достаточно сложные устройства, не полностью устраняющие межсимвольные искажения и вносящие значительные задержки в процессе принятия решений по наблюдаемым данным о переданных дискретных сообщениях.

В рассматриваемом модеме в каждом индивидуальном частотно-ограниченном канале в блоках ФС (рис. 2) формируются такие «медленные» ОФС, которые принципиально не содержат межсимвольных искажений [4]. Однако, проходя далее по каналу прямой связи (КПС), ОФС искажаются из-за неравномерности его АЧХ и ФЧХ (рис. 1). Для устранения или компенсации этих искажений встает задача оптимальной оценки комплексного коэффициента передачи КПС. Перейдем к решению этой задачи.

Уравнения наблюдения канала связи

В режиме вхождения в связь из блока генератора сетки частот через блок БВС (рис. 2) в КС поступает полигармонический сигнал с единичными амплитудами и нулевыми начальными фазами:

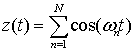Тогда отклик стационарного КС представляется в виде:

(8)

где , - амплитуды и начальные фазы колебаний, подлежащие оценке и определяемые АЧХ и ФЧХ канала связи (рис. 1).

Применяя в блоке БОП КПС к когерентное детектирование с опорным колебанием или любой метод преобразования частоты из области верхних в область нижних частот, приходим к низкочастотному эквиваленту (НЧЭ) сигнала

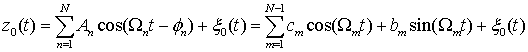, (9)

где , , , - низкочастотный эквивалент АБГШ.

Рассматривая в дискретном времени , формула (9) преобразуется к виду

, (10)

где введены следующие обозначения:

, , (11)

, , , , - интервал дискретизации.

Перейдем к вопросам оценки векторного параметра канала связи.

Рекуррентная оценка параметров шумового канала связи по известному тестовому сигналу

Для получения рекуррентной оценки параметров частотно-ограниченного канала связи при наличии шума наблюдения часто задаются уравнением состояния модели оценки [8]. Полагаем, что уравнение состояния представляется рекуррентным уравнением вида

(12)

где - мерный вектор шума оценки, являющийся гауссовской векторной случайной величиной с нулевым средним и корреляционной матрицей , - единичная матрица размера , - дисперсия шума модели оценки.

Ставится задача найти оценку вектора состояния , оптимальную по критерию минимума среднеквадратической погрешности, с учетом уравнения наблюдения (10). Для получения оптимальной регуляризованной оценки воспользуемся минимизацией эмпирического риска в форме функционала Тихонова [9]

, (13)

где - параметр регуляризации, - апостериорная корреляционная матрица погрешности оценки параметров модели (11).

С учетом (12), искомая оптимальная оценка ищется по критерию

. (14)

Дифференцируя (13) по и приравнивая производные нулю, после ряда преобразований получаем рекуррентный алгоритм оценки в виде следующих уравнений:

, (15)

(16)

(17)

, (18)

с начальными условиями: , , где - априорная корреляционная матрица погрешности оценки.

При отсутствии полигармонического тестового сигнала наблюдению подлежит только шум наблюдения, т.е. . Полагаем, что шум наблюдения представляет собой стационарный некоррелированный случайный процесс. Тогда для оценки его дисперсии можно воспользоваться следующим рекуррентным соотношением [8]:

(19)

Уравнения (15)÷(19) полностью решают задачу оптимальной рекуррентной оценки параметров частотно-ограниченного шумового канала связи.

По оценкам величин далее вычисляются оценки амплитуд АЧХ кс и фаз ФЧХ КС.

Оценки фаз {} из блока БОП КПС поступают на управляющий вход генератора сетки частот демодулятора для их компенсации при работе модема в режиме передачи информации (рис. 2). Оценки амплитуд {} из блока БОП КПС в режиме вхождения в связь с передающим модемом по каналу обратной связи поступают на управляющие входы усилителей, коэффициенты усиления которых выбираются обратно пропорциональными оценкам амплитуд КС, т.е. . Управление усилителями на передаче, а не на приеме приводит к выравниванию коэффициентов передачи КС в частотной области и перераспределению величин отношения сигнал/шум (ОСШ) по каждому из индивидуальных каналов интеллектуального модема.

Экспериментальная оценка параметров модели канала связи

Результаты проверки работоспособности метода рекуррентной оценки параметров шумового канала связи по известному полигармоническому сигналу получены с использованием системы MATLAB и иллюстрируются на рисунке 5 при ОСШ 0 дБ.

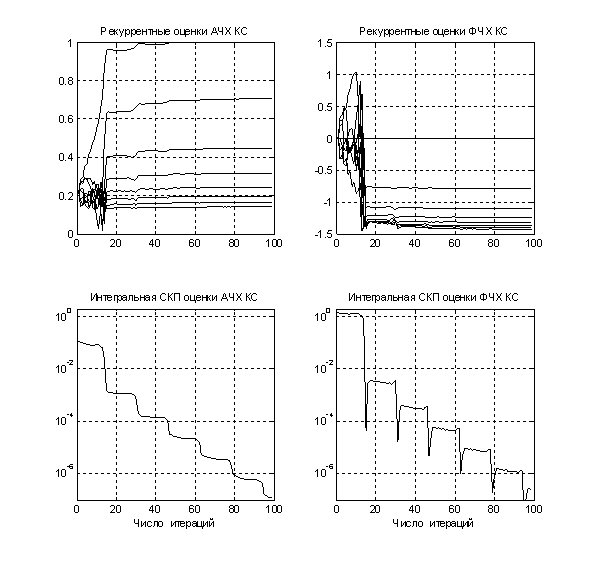
Рис. 5 – Результаты экспериментального исследования алгоритма рекуррентной оценки параметров модели канала связи

В качестве модели низкочастотного эквивалента канала связи выбран фильтр первого порядка с комплексным коэффициентом передачи вида:

, (20)
где - АЧХ, а - ФЧХ НЧЭ модели КС, .

Для цифровой реализации выбрано каналов, на частотах . В этом случае значения оцениваемых амплитуд и фаз модели НЧЭ КС приведены в таблице 1.

Таблица 1 – Оцениваемые параметры НЧЭ модели канала связи

0	1	2	3	4	5	6	7
1	0.70711	0.44721	0.31623	0.24254	0.19612	0.16440	0.14142
0	-0.7854	-1.1071	-1.2490	-1.3258	-1.3734	-1.4056	-1.4289

В качестве тестового сигнала на входе НЧЭ КС использовался полигармонический сигнал вида: 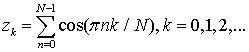. Тогда отклик модели КС в соответствие с (8) равен

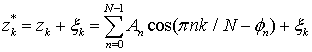. (21)

В качестве шумового сигнала моделировался некоррелированный гауссовский шум с дисперсией . Наблюдаемый на приеме сигнал характеризуется отношением сигнал/шум (ОСШ), выбранный равным дБ, где - соответственно, средние мощности сигнала и шума.

На рисунке 5 приведены графики, полученные согласно (14)-(17), рекуррентных оценок амплитуд {} (график верхний слева) и фаз {} (график верхний справа) при нулевом ОСШ дБ и . На нижних графиках приведены данные текущих интегральных среднеквадратических отклонений (СКО) оценок амплитуд и фаз от их априорных значений (таблица 1), определяемых следующим образом:

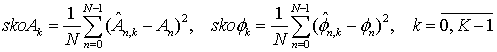, (22)

где - число итераций.

Апостериорная интегральная дисперсия оценки комплексного коэффициента передачи КС, определяемая по (15) и равная 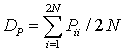, зависят от ОСШ в канале связи. Результаты этой зависимости для проведенного эксперимента приведены в таблице 2.

Таблица 2 – Зависимость апостериорной дисперсии оценки коэффициента передачи КС от ОСШ

ОСШ

(дБ)

-15

-10

-5

D_P

3.86

1.22

3.88∙10^-1

1.24∙10^-1

4.09∙10^-2

1.44∙10^-2

5.86∙10^-3

2.91∙10^-3

1.37∙10^-3

В работе [9] доказано, что рекуррентные оценки параметров, получаемые на основе минимизации эмпирического риска в форме функционала Тихонова (13) являются асимптотически оптимальными по критерию минимума среднеквадратической погрешности, т.е. асимптотически несмещенными и эффективными. Результаты проведенного исследования на примере оценки амплитуд и фаз НЧЭ КС полностью подтверждают этот вывод, что иллюстрируется экспериментальными данными, приведенными на рисунке 5 и в таблице 2.

5. Расчет эффективности и помехоустойчивости модема

Эффективность модема характеризуется максимально возможной скоростью передачи цифровых данных по КС, а помехоустойчивость – средней вероятностью ошибки на бит или символ. Рассмотрим эти вопросы применительно к рассматриваемому модему на основе работы автора [10]. Так, выбирая в каждом индивидуальном канале многочастотного модема в качестве НЧЭ фильтр Баттерворта восьмого порядка (ФБ-8) (см. рис. 4), из [10] находим зависимость коэффициента передачи по энергии (КПЕ) от скорости передачи в виде:

(23)

где - энергии ОФС на входе и выходе ФБ-8, - множитель Лагранжа в (7). График зависимости КПЕ от величины для ФБ-8 при кГц показан на рисунке 6.

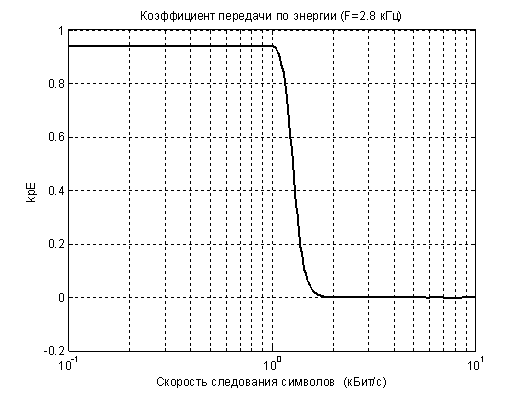
Рис. 6 – Зависимость КПЕ от скорости передачи символов при кГц

Изменяя частоту ФБ-8, находим величину из (23). Результаты сведены в таблицу 3.

Таблица 3 Значения скорости передачи ОФС от граничной частоты ФБ-8

№	(кГц)	(кбит/с)	№	(кГц)	(кбит/с)	№	(кГц)	(кбит/с)	№	(кГц)	(кбит/с)
1	0.03	1.0902∙10^-²	16	0.9	3.2573∙10^-¹	31	2.4	8.6207∙10^-¹	46	3.9	1.3889
2	0.04	1.4535∙10^-²	17	1.0	3.6232∙10^-¹	32	2.5	9.0090∙10^-¹	47	4.0	1.4286
3	0.05	1.8169∙10^-²	18	1.1	3.9841∙10^-¹	33	2.6	9.3458∙10^-¹	48	4.1	1.4706
4	0.06	2.1801∙10^-²	19	1.2	4.3478∙10^-¹	34	2.7	9.7087∙10^-¹	49	4.2	1.4925
5	0.07	2.5432∙10^-²	20	1.3	4.6948∙10^-¹	35	2.8	1.0101	50	4.3	1.5385
6	0.08	2.9070∙10^-²	21	1.4	5.0505∙10^-¹	36	2.9	1.0417	51	4.4	1.5625
7	0.09	3.2701∙10^-²	22	1.5	5.4348∙10^-¹	37	3.0	1.0753	52	4.5	1.6129
8	0.1	3.6337∙10^-²	23	1.6	5.7803∙10^-¹	38	3.1	1.1111	53	4.6	1.6393
9	0.2	7.2622∙10^-²	24	1.7	6.1350∙10^-¹	39	3.2	1.1494	54	4.7	1.6667
10	0.3	1.0893∙10^-¹	25	1.8	6.4935∙10^-¹	40	3.3	1.1905	55	4.8	1.7241
11	0.4	1.4514∙10^-¹	26	1.9	6.8493∙10^-¹	41	3.4	1.2195	56	4.9	1.7544
12	0.5	1.8149∙10^-¹	27	2.0	7.1942∙10^-¹	42	3.5	1.2500	57	5.0	1.7857
13	0.6	2.1739∙10^-¹	28	2.1	7.5758∙10^-¹	43	3.6	1.2987	58	5.1	1.8182
14	0.7	2.5381∙10^-¹	29	2.2	7.9365∙10^-¹	44	3.7	1.3333	59	5.2	1.8519
15	0.8	2.8986∙10^-¹	30	2.3	8.2645∙10^-¹	45	3.8	1.3699	60	5.3	1.8868

На рисунке 7 приведены графики зависимости скорости передачи ОФС от граничной частоты ФБ-8 для двух случаев: а) по данным таблицы 3 (красные точки), б) по результатам линейной аппроксимации данных таблицы 3 (сплошная линия), удовлетворяющих следующему соотношению:

, (24)

где величина в соответствии с методом наименьших квадратов равна . При этом минимальная СКП аппроксимации равна .

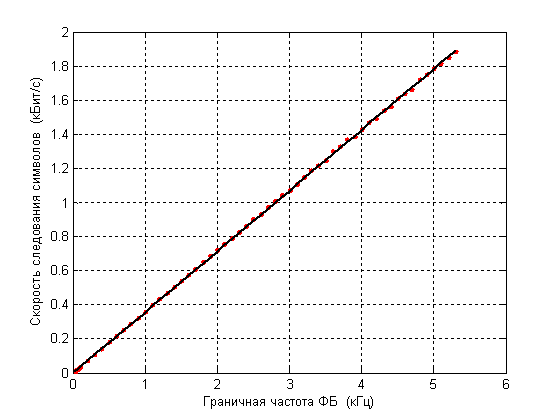
Рис. 7 – Зависимость скорости передачи ОФС от граничной частоты ФБ-8

Спектральная эффективность модема или эффективность использования полосы частот КС выражается удельной скоростью передачи , равной количеству переданных бит в секунду на один герц полосы (бит/(с∙Гц)) [11]. Для получения этой величины воспользуемся соотношениями (1) и (24). С учетом (1) находим скорость следования символов

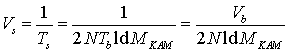. (25)

Теперь с учетом (24), полагая в (25) , находим величину по соотношению

, (26)

где учтено, что .

Следует отметить, что в соответствие с (23) и рисунком 6, при величина КПЕ постоянна и равна . При величина быстро уменьшается до нуля. Поэтому оценку помехоустойчивости модема будем рассчитывать при скорости , удовлетворяющей соотношению (23) с КПЕ, равным .

В этом случае, согласно работе [10], помехоустойчивость передачи символов в каждом индивидуальном канале модема с учетом неравномерности амплитуд АЧХ КС определяется средней вероятностью ошибки на бит следующего вида

, (27)

где - значения АЧХ КС (рис. 1) на центральных частотах индивидуальных каналов модема, - их оценки, - энергия, приходящаяся на один бит передаваемых данных, - односторонняя спектральная плотность мощности АБГШ, - функция ошибки вида

. (28)

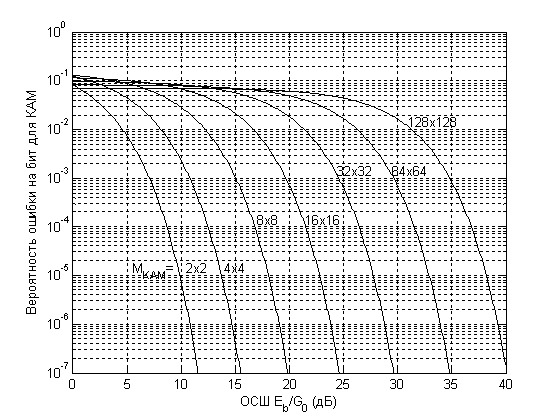
Зависимости (27) для случая, когда АЧХ КС, путем полученных оценок (см. раздел 4), полностью выравнена, характеризуют потенциальную помехоустойчивость многочастотного модема и показаны на рисунке 8.

Рис. 8 – Зависимости вероятности ошибки на бит от ОСШ для сигналов с КАМ

Покажем, что в случае, когда в модеме коррекция АЧХ (её выравнивание) не проводится (), его помехоустойчивость падает в зависимости от показателя неравномерности АЧХ.

Для примера, в качестве модели НЧЭ АЧХ КС примем соотношение (20), согласно которому значения АЧХ примем равными . Выбирая , , и , окончательно значения АЧХ представим в виде

, (29)

где - показатель неравномерности АЧХ, значения которого представлены во второй строке таблицы 4.

Таблица 4 – Показатель неравномерности модели НЧЭ АЧХ КС

0.25

0.1111

0.0625

0.04

0.0278

0.0204

0.0156

1.084∙10^-1

3.498∙10^-²

1.099∙10^-²

3.586∙10^-3

1.287∙10^-3

5.25∙10^-4

2.461∙10^-4

1.318∙10^-4

Подставляя выражение (29) в (27) и фиксируя параметр , определяем среднее значение вероятности ошибки на бит, обеспечиваемой в многочастотном модеме при :

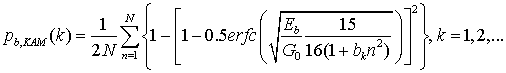(30)

Графики зависимости (30) для различных приведены на рисунке 8.

Рис. 9 – Зависимости вероятности ошибки на бит от ОСШ для сигналов с при различных показателях неравномерности АЧХ КС

Из графиков рисунка 9 следует, что при увеличении показателя неравномерности АЧХ помехоустойчивость модема существенно падает. Расчеты зависимости от , при фиксированном ОСШ=10 дБ, представлены в третьей строке таблицы 4. Так, при увеличении от до , вероятность ошибки увеличивается с 1.318∙10^-4 до 1.084∙10^-1. Следовательно, для повышения помехозащищенности модема (уменьшения средней вероятности ошибки) актуальной является задача выравнивания характеристик КС на основе оптимальной полигармонической фильтрации их параметров (см. раздел 4).

В заключение этого раздела рассмотрим вопрос близости показателя спектральной эффективности рассмотренного модема к его предельному значению. Согласно работе Шеннона [12], спектральная эффективность системы связи, работающей в условиях гауссовского канала связи, удовлетворяет эквивалентным неравенствам:

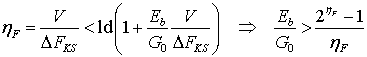. (31)

Граничная зависимость Шеннона от величины ОСШ приведена на рисунке 10.

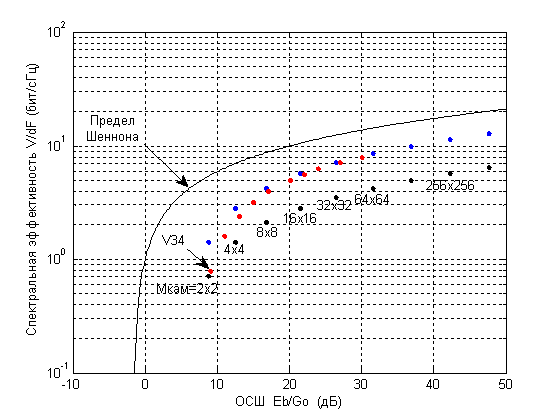
Рис. 10 – Зависимость спектральной эффективности модема от ОСШ при

Для оценки спектральной эффективности рассматриваемого модема воспользуемся соотношениями (26) и (27). Часто эффективность практических модемов оценивается при фиксированном значении допустимой вероятности ошибочного приема, равного [2,11]. Поэтому, принимая в (27) , получаем следующее соотношение для ОСШ , как функции от и ,

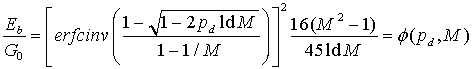, (32)

где - функция, обратная функции ошибки в (28).

При этом согласно (26), спектральная эффективность модема равна

. (33)

Результаты расчета спектральной эффективности модема по (33) с учетом (32) представлены на рисунке 10 (черные точки) и сведены в таблицу 5.

Таблица 5 – Зависимость спектральной эффективности модема при от ОСШ

	1	2	3	4	5	6	7	8	9
	2	4	8	16	32	64	128	256	512
ОСШ (дБ)	8.6785	12.485	16.8	21.482	26.42	31.539	36.789	42.138	47.563
(бит/с∙Гц)	0,7134	1.4268	2.1402	2.8536	3.567	4.2804	4.9938	5.7072	6.4206

Для сравнения на рисунке 10 приведены также данные спектральной эффективности для практического модема стандарта V.34 (красные точки). Анализ полученных результатов показывает, что предлагаемый модем с и модем стандарта V.34 для ОСШ, равного 9 дБ, равнозначны по спектральной эффективности. Для сигналов с модем V.34 спектрально более эффективен. Однако модернизация предлагаемого модема путем применения преобразования Гильберта к ОФС из (5) позволяет повысить спектральную эффективность многочастотного модема в два раза, как это показано на рисунке 10 (синие точки), но это требует другого исследования.

6. Заключение

В работе предложен метод передачи дискретных сообщений в системе цифровой связи с использованием модема с многочастной модуляцией, сравнимый с лучшими стандартными модемами. Новизна метода определяется использованием оптимальных финитных сигналов, не вызывающих межсимвольных искажений в индивидуальных каналах модема, и максимизирующих ОСШ на входе фильтров демодулятора, согласованных с оптимальными финитными сигналами модулятора. Оптимальная настройка параметров модема в условиях частотно-ограниченного шумового канала связи осуществляется по рекуррентным оценкам амплитуд и фаз АЧХ и ФЧХ канала связи с использованием канала обратной связи в режиме вхождения в связь. Проведен не приближенный, но точный теоретической расчет эффективности и помехоустойчивости модема.

Литература

1. Зяблов В.В., Коробков Д.Л., Портной С.Л. Высокоскоростная передача сообщений в реальных каналах. – М.: Радио и связь, 1991. – 288 с.

2. Лагутенко О.И. Современные модемы. – М.: Эко-Трендз, 2002. – 344 с.

3. Балашов В.А., Воробиенко П.П., Ляховецкий Л.М. Системы передачи ортогональными гармоническими сигналами. – М.: Эко-Трендз, 2012. – 228 с.

4. Санников В.Г. Интеллектуальный модем на основе многочастотной модуляции // Доклады VIII Всероссийской научно-технической конференции «Радиолокация и радиосвязь», 24-26 ноября 2014 г., Москва. – С. 119–123.

5. Санников В.Г. Синтез финитных сигналов Найквиста, согласованных с телефонным каналом связи // «ЭЛЕКТРОСВЯЗЬ». – 2012. – № 5. – С. 9-12.

6. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. – М.: «НАУКА», ГР ФМЛ, 1971. – 1108 с.

7. Санников В.Г. Метод оптимизации радиотелефонной связи // Журнал Радиоэлектроники: электронный журнал. 2014, № URL: http: // ire.cplire.ru / jre / nov 14 / 17 / text.pdf.

8. Роберт ЛИ. Оптимальные оценки, определение характеристик и управление / Пер. с англ. Ю.Ф. Кичатова и Л.П. Сысоева. – М.: Изд. «НАУКА», ГР ФМЛ, 1966. – 176 с. (Серия «Теоретические основы технической кибернетики»).

9. Шлома А.М. О решении операторных уравнений при неполной информации // Журнал вычислительной математики и математической физики. – 1966. Т. 36. № 3. – С. 15 – 27.

10. Санников В.Г. Помехоустойчивость системы передачи оптимальных финитных сигналов по телефонному каналу связи // «ЭЛЕКТРОСВЯЗЬ». – 2013. – № 5. – С. 39-44.

11. Феер К. Беспроводная цифровая связь. Методы модуляции и расширения спектра: Пер. с англ. / Под ред. В.И. Журавлева. – М.: Радио и связь, 2000. – 520 с.

12. Шеннон К. Работы по теории информации и кибернетике: Пер. с англ. / Под ред. Р.Л. Добрушина и О.Б. Лупанова с предисловием А.Н. Колмогорова. – М.: Издательство иностранной литературы, 1963. – 830 с.