УДК 621.372.2, 537.876.45
Анализ работы пассивного лучеводного спектрометра с охлаждаемым селективным прИемником
В. В. Завьялов
Институт физических проблем им. П.Л. Капицы РАН,
Московский физико-технический институт (государственный университет)
Статья получена 3 января 2015 г.
Аннотация. Представлена методика расчета потоков излучения и выведены формулы для вычисления коэффициентов отражения (R) и пропускания (T) образцов при использовании пассивного спектрометра, состоящего из холодной (с температурой жидкого гелия) и теплой (с комнатной температурой) камер, соединенных между собой лучеводом. Селективный приемник располагается в холодной камере. В теплой камере, перекрывая апертуру многоволновой моды лучевода и по нормали к ней, помещен механический зеркальный обтюратор, позволяющий использовать модуляционную методику и синхронное детектирование сигналов. При измерениях с образцом, он устанавливается а) перед обтюратором и б) после обтюратора. Полученные при этих позициях сигналы от селективного приемника позволяют вычислить коэффициенты R и T образца. Данная методика предназначена для работы со слабым тепловым излучением терагерцового диапазона длин волн, в котором охлаждаемые приемники практически не имеют альтернативы, а активная спектроскопия с использованием интенсивного источника излучения затруднена или нежелательна.
Ключевые слова: терагерцовая спектроскопия, пассивная спектроскопия, радиометрия, тепловое излучение, лучевод.
Abstract. The procedure of measurements and the formulas for calculating the sample's reflection (R) and transmission (T) coefficients with the use of a passive terahertz spectrometer are presented. The passive spectrometer comprises of cold and room-temperature chambers interconnected via a multimode waveguide (light pipe). Spectral selective liquid helium-cooled detector is placed at the cold side, and a specular disk shutter is positioned near the room-temperature end of the light pipe. The metered coefficients R and T can be calculated as a result of the two consecutive synchronous detection measurements — with the specimen placed before and after the shutter. Passive terahertz spectrometry based on the selective cooled detectors is a good alternative to active one when the use of a sophisticated teraherz radiation source is difficult or undesirable.
Key words: Terahertz spectroscopy, passive spectroscopy, radiometry, thermal radiation, light-pipe.
Спектрометр называют пассивным, если для определения спектральных зависимостей оптических свойств образца он использует лишь собственное тепловое излучение самого образца. Пассивные спектрометры применяются, например, для изучения атмосферы и ее загрязнения [1,2].
Отдельный интерес представляет случай, когда образец имеет температуру окружающей среды («комнатную» температуру) и находится с ней в тепловом равновесии. При этом справедлив закон Кирхгофа, согласно которому «в любой точке спектрального диапазона излучательная способность тела равна его поглощательной способности и не зависит от формы и химической природы тела». В результате, идущее от образца излучение имеет универсальное, описываемое формулой Планка «черно тельное» спектральное распределение и не несет информации о характеристиках самого образца. Чтобы обойти это ограничение достаточно, чтобы приемник, регистрирующий тепловое излучение от образца, находился при иной, лучше низкой температуре. В терагерцовом диапазоне длин волн для этой цели хорошо подходит, например, перестраиваемый селективный приемник [3], основанный на эффекте циклотронного резонанса электронов в кристалле InSb, работающий при температуре жидкого гелия. Использование терагерцового спектрометра в рассматриваемой нами конфигурации описано в работе [4]. Особый интерес представляет использование неселективных болометров совместно с охлаждаемым фурье-спектрометром.
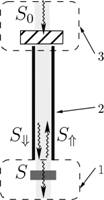

На рис.1 приведена схема, поясняющая принцип учета потоков излучения в пассивном лучеводном спектрометре. Селективный приемник 1 находится в холодной зоне. Многолучевой волноводный канал (лучевод) 2 ведет из холодной зоны в теплую зону 3. Измеряемый образец и прочие элементы спектрометра находятся в тепловом равновесии в теплой зоне, которая может быть заполнена теплообменным газом и имеет комнатную температуру.
При рассмотрении потоков излучения в
спектрометре следует учитывать только те лучи, которые попадают в пределы
многолучевой волновой моды. Диаграмма направленности этой моды формируется, в
основном, исходя из условий распространения излучения в лучеводе, – благодаря
малому поглощению параксиальных лучей при полном подавлении остальных,
испытывающих множественные отражения от стенок лучевода, лучей. Такая модель
хорошо подходит для металлических лучеводов и согласуется с результатами
анализа литературных данных по их оптическим свойствам, – см., например, [5]. В
формировании многолучевой волновой моды участвуют также параксиальные лучи,
отраженные от прочих объектов спектрометра. Эти объекты (приемник, измеряемый
образец, окно, дополнительное зеркало), как предполагается, имеют форму пластин
(пленок) и устанавливаются перпендикулярно оптической оси непосредственно у
концов лучевода. Рассматриваемая волновая мода характеризуется площадью
сечения ![]() и величиной
и величиной ![]() эффективного телесного угла выходящего из лучевода пучка
излучения. Далее мы будем считать, что угол
эффективного телесного угла выходящего из лучевода пучка
излучения. Далее мы будем считать, что угол ![]() достаточно
мал, чтобы оставаться в рамках параксиального приближения.
достаточно
мал, чтобы оставаться в рамках параксиального приближения.
Определим величину потоков теплового
излучения многолучевой волноводной моды вблизи холодного конца лучевода. Встречные
потоки идущего по лучеводу излучения ![]() и
и
![]() выражаются так:
выражаются так: ![]() ,
, ![]() . Здесь
. Здесь ![]() – энергетический коэффициент отражения от объектов,
находящихся в теплой зоне над верхним концом лучевода,
– энергетический коэффициент отражения от объектов,
находящихся в теплой зоне над верхним концом лучевода, ![]() – коэффициент отражения от элементов холодной зоны,
– коэффициент отражения от элементов холодной зоны, ![]() – коэффициент пропускания лучевода. Член
– коэффициент пропускания лучевода. Член ![]() , записанный для потока равновесного теплового излучения
объектов в теплой зоне, удовлетворяет волноводной форме закона Кирхгофа [6].
Что касается теплового излучения объектов в холодной зоне, то оно, при
использовании охлаждаемых до гелиевых температур приемников, является
несущественным, хотя в рамках данной модели его учет не представляет сложности.
В результате, поток излучения, выходящий из лучевода в холодную зону на
селективный приемник, можно записать в виде функции от
, записанный для потока равновесного теплового излучения
объектов в теплой зоне, удовлетворяет волноводной форме закона Кирхгофа [6].
Что касается теплового излучения объектов в холодной зоне, то оно, при
использовании охлаждаемых до гелиевых температур приемников, является
несущественным, хотя в рамках данной модели его учет не представляет сложности.
В результате, поток излучения, выходящий из лучевода в холодную зону на
селективный приемник, можно записать в виде функции от ![]() :
:
![]() (1)
(1)
Эта функция позволит нам далее проводить вычисления при различных сочетаниях устанавливаемых вблизи верхнего конца лучевода объектов в теплой зоне.
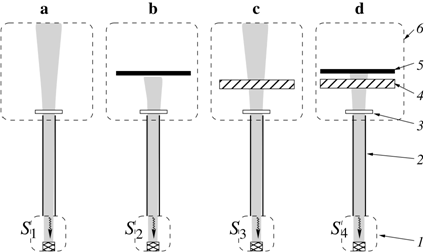
Рис. 2. Набор позиций, поясняющих работу
спектрометра.
1– холодная зона с приемником излучения;
2– многолучевой
волноводный канал; 3– окно;
4– образец в виде пластины или пленки; 5–
зеркало.
6– зона равновесного теплового излучения комнаты.
S1 ,
S2, S3, S4 – потоки излучения, прошедшие на
приемник.
Рассмотрим приведенные на рис.2 позиции объектов теплой зоны спектрометра и определим для каждой из них величину проходящего на приемник потока излучения. Измерив эти потоки, мы, далее, сможем вычислить спектральные энергетические характеристики измеряемого образца. При суммировании отраженных волн от объектов в теплой зоне спектрометра (образца, герметизирующего окна, дополнительного зеркала) мы будем для простоты считать излучение некогерентным, что справедливо, если длина когерентности, определяемая спектральным разрешением селективного приемника, достаточно мала. В то же время, спектральные характеристики самих элементов в спектрометре (измеряемый образец, окна), которые могут быть достаточно тонкими, могут проявлять интерференционный характер.
a) Верхний конец лучевода герметизирован
окном, имеющим известные спектрально зависимые коэффициенты пропускания ![]() и отражения
и отражения ![]() .
Так как это окно в данной позиции является единственным установленным в теплой
зоне объектом, то
.
Так как это окно в данной позиции является единственным установленным в теплой
зоне объектом, то ![]() и проходящее на приемник излучение,
согласно (1), равно:
и проходящее на приемник излучение,
согласно (1), равно:
![]() (2)
(2)
b) На верхнем конце лучевода над окном добавлено
зеркало. Расчет суммарного отражения этой пары дает ![]() и, следовательно,
и, следовательно,
![]() (3)
(3)
c) На верхнем конце лучевода над окном установлен
измеряемый образец, искомые коэффициенты пропускания отражения и поглощения
которого: ![]() ,
, ![]() ,
,
![]() . В этом случае
. В этом случае
![]() и, следовательно,
и, следовательно,
![]() (4)
(4)
d) На верхнем конце лучевода над окном и измеряемым образцом поставлено зеркало. Вычислив коэффициент отражения от этой трехэлементной системы, получим аналогично:
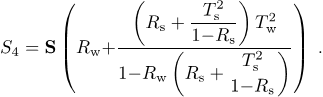 (5)
(5)
Оптические характеристики образца можно вычислить из результатов отдельных измерений, проведенных при рассмотренных на рис.2 позициях объектов в теплой зоне спектрометра. Если вместо стационарного зеркала взять механический зеркальный обтюратор, то вся процедура сводится к трем измерениям (см. рис.3), в каждом из которых попеременно, с частотой модуляции обтюратора, регистрируется разностный сигнал от следующих пар позиций:
• ![]() – «калибровка», – установлен только зеркальный обтюратор;
– «калибровка», – установлен только зеркальный обтюратор;
• ![]() – «отражение», – образец поставлен перед обтюратором;
– «отражение», – образец поставлен перед обтюратором;
• ![]() – «на проход», – образец установлен за обтюратором.
– «на проход», – образец установлен за обтюратором.
Следует отметить, что такая процедура, кроме всего прочего, позволяет использовать чувствительную модуляционную методику измерений с синхронным детектированием слабого сигнала с приемника.
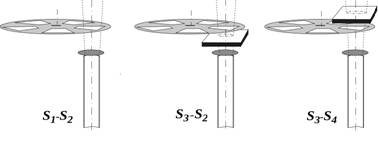
Рис. 3. Процедура измерений с зеркальным обтюратором при различных позициях измеряемого образца.
Введем величины ![]() и
и ![]() ,
значение которых получаются в результате измерений:
,
значение которых получаются в результате измерений:
![]() (6)
(6)
Решая систему алгебраических уравнений (1,3-7) получаем:
![]() (7)
(7)
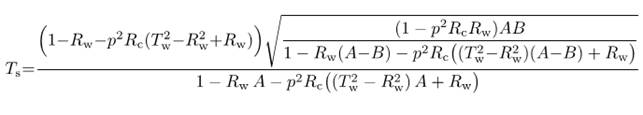 (8)
(8)
Отметим, что в формулу для ![]() входит лишь
входит лишь ![]() ,
то есть данные в позиции
,
то есть данные в позиции ![]() –
«отражение», что позволяет производить непрерывный контроль за изменением
отражения от образца без смены его позиции в спектрометре. При этом вначале
достаточно измерить калибровочные данные в позиции
–
«отражение», что позволяет производить непрерывный контроль за изменением
отражения от образца без смены его позиции в спектрометре. При этом вначале
достаточно измерить калибровочные данные в позиции ![]() .
.
Возможной альтернативой при выборе позиций может служить более сложное сочетание из четырех объектов с дополнительным зеркалом (на рис.2 и 3 не показано), а именно:
• (![]() ) – «на проход с отражением», – окно
) – «на проход с отражением», – окно![]() обтюратор
обтюратор![]() образец
образец![]() зеркало.
зеркало.
В такой конфигурации измеряемым
сигналом является ![]() , а коэффициент пропускания
вычисляется по формуле:
, а коэффициент пропускания
вычисляется по формуле:
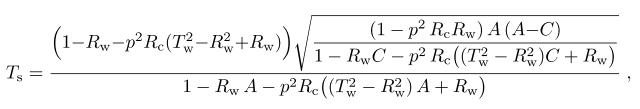 (9)
(9)
которая совпадает с (8), потому что,
как легко заметить, ![]() .
.
Особый интерес представляет случай,
когда величина ![]() (коэффициент пропускания лучевода)
мала. В этом случае многократно-отраженные лучи в лучеводе ослаблены и формулы
(7-9) упрощаются:
(коэффициент пропускания лучевода)
мала. В этом случае многократно-отраженные лучи в лучеводе ослаблены и формулы
(7-9) упрощаются:
 (10)
(10)
Замечательным свойством этого
предельного случая является то, что результат, с точностью до членов
разложения порядка ![]() , перестает зависеть от такой
трудно-определимой спектрально-зависимой величины как
, перестает зависеть от такой
трудно-определимой спектрально-зависимой величины как ![]() (коэффициент отражения от элементов холодной зоны). Однако
на практике это означает, также, и сильное ослабление измеряемых приемником
сигналов
(коэффициент отражения от элементов холодной зоны). Однако
на практике это означает, также, и сильное ослабление измеряемых приемником
сигналов ![]() ,
, ![]() ,
,
![]() .
.
Приложение.
При выборе приемника излучения
полезно иметь представление об абсолютной интенсивности «чернотельного»
теплового излучения ![]() (см. рис.1), поступающего из теплой
зоны.
(см. рис.1), поступающего из теплой
зоны.
Величину этого потока, зависящего от
угловой апертуры ![]() и сечения
и сечения ![]() в частотном интервале
в частотном интервале ![]() можно
оценить в соответствии с [7]:
можно
оценить в соответствии с [7]:
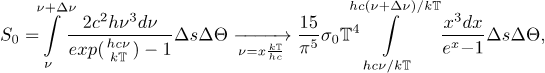 (11)
(11)
где ![]() –
температура,
–
температура,
![]() – постоянная Стефана-Больцмана, а
частоты
– постоянная Стефана-Больцмана, а
частоты ![]() измеряются в обратных длинах волн.
измеряются в обратных длинах волн.
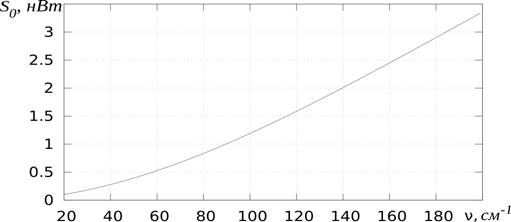

На рис.4 приведен
рассчитанный по этой формуле график спектральной зависимости мощности потока
теплового излучения ![]() для типичных параметров апертуры
лучевода реального прибора [3]:
для типичных параметров апертуры
лучевода реального прибора [3]: ![]() ,
,
![]() ,
, ![]() .
.
Литература
1. Rodgers C.D., «Retrieval of Atmospheric Temperature and Composition From Remote Measurements of Thermal Radiation» // Rev. Geophysics and Space Physics, vol. 14, pp. 609-624, Nov. 1976.
2. Kikuchi K., Kohjiro S., Yamada T., Shimizu N. and Wakatsuki A., «Compact terahertz passive spectrometer with wideband superconductor-insulator-superconductor mixer» //Rev Sci. Instr. Vol. 83, 023110, 2012.
3. Богомолов Г.Д., Завьялов В.В., Зотова Е.А., Шампаров Е.Ю., «Быстродействующий перестраиваемый детектор излучения субмиллиметрового диапазона на циклотронном резонансе в InSb» // ПТЭ 2002, вып. 1, стр.87-95.
4. Родэ, С.В., Шампаров Е.Ю. Установка для быстрой терагерцовой спектрометрии тонких диэлектрических материалов // Дизайн и технологии. 2010. № 18. С. 47-52.
5. Hawthorn D.G. and Timusk T., «Transmittance of skew rays through metal light pipes» // Appl. Opt., vol. 38, no. 13, pp. 2787—2794, May 1999.
6. Рытов С.М., Кравцов Ю.А., Татарский В.И. Введение в статистическую радиофизику, ч.2, гл.3, М.:Наука 1978.
7. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: том V, Статистическая физика, 5-е изд., ч.I, §63. М.: ФИЗМАТЛИТ 2002.