УДК 621.396.67.012.12
Методическая и шумовая погрешности восстановления диаграммы направленности антенны при измерениях в неидеальных условиях, представимых сходящимся пучком плоских волн
Ю. И. Чони1, И. Ю. Данилов2
1 Казанский национальный исследовательский технический университет им. А.Н. Туполева − КАИ
2 АО ”Информационные спутниковый системы им. академика М.Ф. Решетнёва”
Статья поступила в редакцию 12 декабря 2015 г.
Аннотация. Анализируется влияние методических и технических факторов на точность восстановления диаграммы направленности (ДН) антенны, измеренной в неидеальных условиях, под которыми понимаются любые отличия облучающего поля от плоской волны, в частности, из-за относительно близкого расположения вспомогательной антенны. Процедура восстановления ДН включает реконструкцию облучающего поля в виде сходящегося пучка плоских волн путем измерения и обработки сигнал от зонда, перемещаемого по граничной поверхности рабочей зоны. На примерах двухмерной скалярной задачи исследуется устойчивость задачи восстановления ДН, потенциальная точность и влияние погрешностей измерений, демонстрируются рельефы полей пучков волн внутри и вне рабочей зоны в вариантах цилиндрической или сферической облучающей волны. Представлены зависимости, позволяющие оценить достижимую точность восстановления ДН.
Ключевые слова: диаграмма направленности, сходящийся пучок плоских волн, алгоритм восстановления, погрешности, устойчивость, точность.
Abstract: The paper discusses methodological aspects, computing peculiarities and technical factors with regard to their impact on the accuracy of antenna pattern retrieval through the data, measured in non-ideal environments. We mean any circumstances giving rise to differences between the field in the working area and the ideal plane wave in the first place, a rather short distance from the illuminating antenna. The pattern retrieval procedure is based on the illuminating field reconstruction in the form of a converging cluster of plane waves. It is obtained by processing the data from the probe that is moved along the boundary surface of the working area. With regard to the two-dimensional scalar tasks we investigate the stability of a pattern retrieval problem, potential accuracy and the influence the of measurement errors. In cases cylindrical or spherical illuminating wave, the resultant fields of converging cluster of plane waves inside and outside the working area are demonstrated. The evaluation of the achievable retrieval accuracy is presented.
Key words: antenna radiation pattern, converging cluster of plane waves, antenna measurement accuracy, reconstruction algorithm, stability, precision.
1. Введение
Современные векторные анализаторы цепей позволяют в автоматическом режиме проводить амплифазометрические измерения с последующей цифровой обработкой данных. Благодаря этому, находят применение процедуры реконструкции диаграммы направленности (ДН) антенн при измерениях в далеко неидеальных условиях, когда облучающее поле существенно отличается от плоской волны из-за малого расстояния до вспомогательной антенны и/или отражений от стен. Тридцатилетней давности первые работы в этом направлении носили скорее теоретический, чем практический характер [1 − 2].
С тех пор выполнено немало работ, касающихся различных аспектов первичных измерений и алгоритмов обработки данных, например, [3]. Недавно защищенные диссертации [4, 5] подтверждают актуальность исследований в этой области и в наши дни. В работе [4] выделены три группы методов реконструкции ДН: 1) плоско параллельное сканирование ближнего поля антенны с пересчетом в дальнюю зону, 2) измерение поля антенны в зоне Френеля с пересчетом в дальнюю зону, 3) обследование облучающего поля в рабочей области с помощью антенны или зонда с известной ДН для последующей коррекции ДН испытуемой антенны. Рассматриваемый нами метод сходящегося пучка плоских волн (СППВ) относится к третьей группе, в отечественной литературе именуемой методом эталонной антенны [2], а в англоязычной − «test zone field compensation», что полнее отражает суть дела.
2. Идеология сходящегося пучка плоских волн
Возможность использования СППВ для аппроксимации поля в области, лишенной источников, базируется на двух обстоятельствах [3]. Во-первых, функция Грина свободного пространства и вместе с ней произвольное поле в любой области вне источников представимы интегральным преобразованием
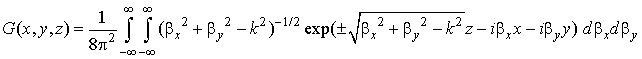
которое
с физической точки зрения есть сплошный телесный (двумерный) пучок плоских
электромагнитных волн, разбегающихся от расположенного в начале координат
источника. Этот пучок включает в себя как однородные (
),
так и поверхностные (
) волны. При антенных измерениях
неоднородности, способные порождать поверхностные волны, значительно удалены от
испытуемой антенны. Поэтому их вкладом в облучающее поле можно пренебречь, и
представить его в рабочей области как СППВ (сходящийся, т.к. источники поля
расположены за ее пределами). Во-вторых,
поскольку реакцию антенны на однородную плоскую волну определяет ее ДН, то
сигнал на выходе антенны, облучаемой СППВ, дается интегралом типа свертки,
ядром которого является ДН антенны.
Ограничимся двухмерной скалярной ситуацией (рис. 1) типичной для подавляющего большинства публикаций на эту тему, когда ДН F(φ) измеряется в плоскости, и облучающее ее поле есть СППВ в той же плоскости. Пусть облучающее поле создается источником цилиндрической волны, расположенным относительно близко в точке D. На первом этапе определяются комплексные амплитуды A(φ) волн пучка, воспроизводящего это поле. Для этого зонд, ДН которого f0(ψ) известна, вращается по окружности радиуса R0 (рис. 1(а)). Здесь «радужное» кольцо изображает СППВ в виде функции A(φ)пространственного спектра волн пучка, но не порождаемое им интерференционное поле. Белая пунктирная стрелка с поперечным отрезком, символизирующим фазовый фронт, изображает отдельную плоскую волну.
Очевидно, что принимаемый зондом сигнал 
связан с функцией A(φ)
интегралом свертки
где 
− угол поворота зонда, 
− ДН зонда, смещенного из
начала координат. По измеренному сигналу 
, из уравнения (1) находят 
.
(а) (б) (в)
Рис. 1. Геометрия задачи: (а) зондирование
сплошного СППВ; (б) измерение ДН в сплошном СППВ;
(в) дискретный СППВ,
зондирование и измерение ДН
На втором этапе вращают испытуемую
антенну, измеряют принимаемый ею сигнал 
и восстанавливают ДН антенны 
, решая аналогичное уравнение свертки
Зонд следует перемещать по поверхности S, охватывающей рабочую зону: R0 > Lа/2. Действительно, усматривая в равенстве (1) совпадение касательных составляющих электрических полей[1] облучающей волны и поля СППВ, на основании теоремы о единственности решения уравнений Максвелла можно утверждать, что в случае цилиндрической облучающей волны поле СППВ точно воспроизводит облучающее поле внутри S. При этом вне S, как показывают расчеты, поле имеет едва ли предсказуемую структуру.
На практике было бы выгодно в качестве вспомогательной антенны использовать источник сферической волны, например, небольшой рупор. При этом теорема единственности побуждает переходить к замкнутой поверхности S и телесному СППВ. Но результаты расчетов свидетельствуют о том, что если речь идет об измерении ДН антенны малого поперечного (относительно плоскости измерений) размера, то и в этом случае аппроксимация облучающего поля плоским пучком дает приемлемые результаты.
3. Вычислительный алгоритм. Аппроксимация облучающего поля
В отсутствии аналитического решения интегральное уравнение сводят к системе линейных алгебраических уравнений (СЛАУ). Простейший прием (едва ли уступающий методу Галеркина-Ритца) − заменить СППВ дискретным пучком из N плоских волн и осуществлять измерения в M > N точках (рис. 1(в)). При этом с учетом кардиоидной ДН зонда уравнение (1) трансформируется в систему M уравнений относительно N неизвестных An = A(φn)
где φn = (n − 1) Δ, φ'm = (m − 1), Δ = 2π/N, δ = 2π/M, и решается, стандартным приемом минимизации среднеквадратичного отклонения.
В моделируемой ситуации имеем: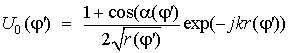 
, где 
− расстояние от источника в
точке D до зонда (см. рис. 1(а)) и 
.
Интересно выяснить, что за поле
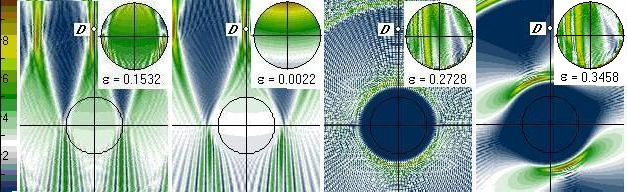
создается СППВ, аппроксимирующим исходящую из точки D цилиндрическую волну? На рис. 2 для
четырех значений числа волн пучка N представлены
нормированные амплитудные рельефы этого поля при следующей геометрии системы: R0 = 7.5
и D =25. Полоска слева на рис. 1(а) − это единая для
всех рисунков палитра близкая к цветовой гамме географической карты: от темно
синего цвета (нулевой уровень) до коричневого (единичный уровень). Рабочая
область S отмечена окружностью радиуса R0, что позволяет судить о масштабе изображений. Справа
вверху каждого рисунка укрупненно воспроизведено поле внутри S, нормированное к локальному
максимуму в S. Среднеквадратичные
отклонения поля пучка E(r,
) от истинного облучающего поля E0(r,) в рабочей области S 
приведены там же.
(а) N = 90 (б) N = 115 (в) N = 130 (г) N = 145
Рис. 2. Амплитудные рельефы полей СППВ: цилиндрическая волна из точки D
Значения N выбраны с таким расчетом, чтобы проиллюстрировать
характерные ситуации. Рис. 2(б)
представляет ситуацию с рациональным числом волн пучка N = 115. При этом линии уровня с визуальной точностью
соответствуют цилиндрической волне, и значение 
свидетельствует о высокой точности
аппроксимации не только амплитуды, но и фазы облучающего поля. Рис. 2(а) соответствует
явно недостаточному числу волн пучка, что проявляется в изрезанности рельефа
поля на периферии области S,
хотя в ее центральной части явственно просматривается цилиндрическая волна. Рис.
2(в) и 2(г) соответствуют другой крайности − излишне большому числу волн
пучка. При этом устойчивость СЛАУ (1')
снижается настолько, что возникает асимметрия поля относительно оси 0у,
разительно проявляющаяся при N = 145.
Эта асимметрия ничем другим не объяснима, кроме как ограниченной точностью вычислений
и представления чисел с плавающей запятой.
Для тех же ситуаций на рис. 3 представлены спектры {A(
)} пучков, аппроксимирующих облучающую
цилиндрическую волну из точки D.
Интервал углов ограничен «передним полупространством» 
. Жирные линии отображают амплитуды, тонкие − фазы волн.
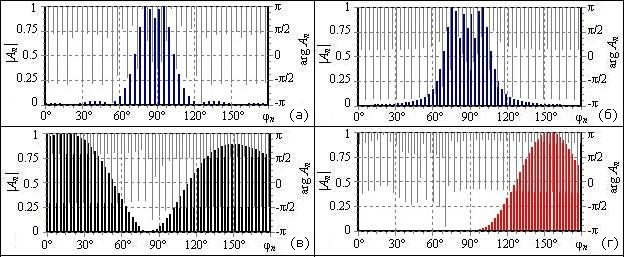
Рис. 3. Комплексные амплитуды {An} волн пучка.
На рис. 3(а), 3(б) (N = 90, N = 115) ожидаемо превалируют волны лучей из окрестности D. При N = 130 (рис. 3(в)) вопреки физике растет интенсивность
поперечных волн ( вблизи 0° и 180°) и появляется асимметрия, резко обостряющаяся
в ситуации N = 145 (рис. 3(г)). За пределами
некоторого углового сектора в окрестности направления = 90° на точку D комплексные
амплитуды соседних волн противофазны (скачки фазы на π), что и порождает «рябь» амплитудного рельефа, ярко
проявляющуюся за пределами области S, а при малом числе волн (рис. 2(а)) даже на ее периферии.
Ясно, что неумеренный рост числа N ухудшает устойчивость СЛАУ (1') из-за уменьшающегося отличия соседних волн на окружности R0 и, следовательно, малого отличия соседних столбцов матрицы СЛАУ. Но происходит это настолько катастрофично, что мы, авторы, потратили массу времени и сил на упорные поиски ошибки в разработанной ими Delphi-программе, интерфейс которой показан на (рис. 4).
Рис. 4. Интерфейс программы исследования алгоритма восстановления ДН
Для выяснения истины были выполнены тестовые расчеты в среде Mathcad, результаты которых (рис. 5) подтвердили состоятельность нашей программы.
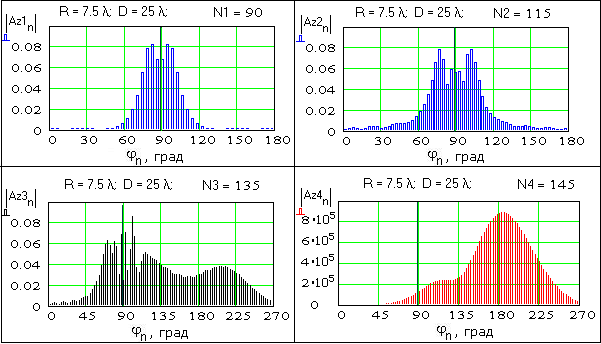
Рис. 5. Пространственные спектры, рассчитанные в среде Mathcad
Естественно, для неустойчивых решений играют роль и формат представления чисел с плавающей запятой, и возможные отличия алгоритмов решения СЛАУ, что приводит к отличиям в деталях, но структурно сопоставляемые решения одинаковы. В области умеренных значений N < 128 решения устойчивы и симметричны. Синий цвет подчеркивает гармоничность этих решений. Их максимальные значения |An|, не подвергнутые нормировке (рис. 5), имеют значения на уровне 0,08.
При N > 130 для нашей программы и N > 135 в случае Mathcad-программы возникает алогичное асимметричное решение (черный цвет). Причем норма решения еще сохраняется на прежнем уровне, что неожиданно, и причина этого заслуживает отдельного исследования. Дальнейшее увеличение числа волн пучка вызывает резко возрастающую асимметрию решения, связанную с его неустойчивостью, закономерным признаком которой служит резкое увеличение нормы решения (на семь порядков при N = 145). Красный цвет подчеркивает катастрофичность этой ситуации, проявляющаяся и в том, что поле пучка за пределами области S на порядки интенсивнее, чем внутри S (рис. 2(г)).
Облучение цилиндрической волной связано с обременительной необходимостью использовать в качестве вспомогательной антенны линейную антенную решетку или линейный раскрыв (пилбокс, например) достаточно большого габарита, ориентированные по нормали к плоскости измерений. Соображения физического толка дают надежду на то, что, если обследуемая антенна имеет малый поперечный размер, то облучающая сферическая волна может быть представлена с помощью СППВ без большого ущерба для воспроизведения реакции испытуемой антенны на облучающую волну. В практическом же плане использование вспомогательной антенны в виде рупора небольших волновых размеров для формирования сферической облучающей волны, чрезвычайно привлекательно.
На рис. 6 приведены поля, возникающие
при аппроксимации в области S сферической
волны, исходящей из точки D. Геометрические
соотношения прежние: R0 = 7.5, D =25. Сигнал зонда в поле сферической волны определялся
очевидной формулой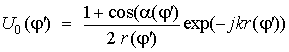 
с учетом обозначений, поясненных на рис.
2. При изменении числа N
волн СППВ проявляются те же закономерности, что и в случае цилиндрической
волны, за тем исключением, что точность аппроксимации сферической волны с
помощью плоского пучка волн существенно скромнее.
(а) N = 90 (б) N = 115 (в) N = 130 (г) N = 145
Рис. 6. Амплитудные рельефы полей СППВ: облучающая сферическая волна
На рис. 7 представлены зависимости 
погрешности восстановления облучающего поля для случаев цилиндрической (а)
и сферической (б) волн. Естественно, СППВ при рационально выбранном числе волн
практически идеально аппроксимирует цилиндрическую волну, в то время, как
точность аппроксимации сферической волны весьма умеренная. В центре рисунков как
визуальные образы соответствующих уровней −55дБ и −15,5дБ погрешности
размещены рельефы полей пучка в S при N
= 115 (жирные штрихи на оси N).
(а) (б)
Рис. 7. Погрешность
аппроксимации облучающего поля
Понятно, что волновой размер поверхности сканирования S предопределяет угловую разрешающую способность при тестировании облучающего поля. Поэтому попытки повысить точность восстановления этого поля за счет уменьшения углового дискрета пучка (увеличения числа волн) оказываются несостоятельными из-за ухудшения обусловленности СЛАУ. Неожиданным является тот выявляемый расчетами факт, что переход от области устойчивых решений к неустойчивым происходит настолько резко, что впору говорить о пороговом эффекте (в моделируемой ситуации при N = 130).
4. Точность восстановления ДН испытуемой антенны
Методические погрешности. Как отмечалось выше, основной фактор, ограничивающий потенциальную точность восстановления ДН антенны в условиях идеальных измерений, − это конечное число N волн пучка и отсчетных точек M. В рамках методологии СППВ число точек M может превышать число N волн пучка[2], обеспечивая определенное усреднение случайных погрешностей измеренных данных. Целесообразно это превышение выбрать кратным: M = K N для упрощения вычислений на этапе восстановления ДН. В расчетных примерах было принято K = 4.
В расчетах, результаты которых приведены ниже, в качестве
испытуемой рассматривалась возбуждаемая равномерно синфазная линейная щелевая
антенна длиной Lа, т.е. линейная антенна из элементов
Гюйгенса с кардиоидными ДН (пунктир на рис. 1(б)). При моделировании сигнал вычислялся интегрированием по Симпсону с точностью до 10−5:
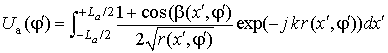в случае цилиндрической волны и 
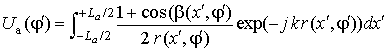в случае сферической волны, где (рис. 1(б)) 
и 
. Сигнал антенны 
связан со спектром пучка волн { An } и истинной ДН антенны 
очевидным образом: 
. N отсчетов, соответствующих индексам m = 1 + (p−1)K + k−1, т.е. N углам 
, где p = 1..N, образуют систему N уравнений относительно N отсчетов ДН с шагом Δ при любом значении k = 1..K, нумерующего отсчет (с шагом 
) в пределах дискрета 
(см. рис. 1(в)). Каждая из этих K СЛАУ приводится к стандартному виду
, (p = 1..N), (2')
если исходные коэффициенты An при n + p > N циклически продолжить: An+p = An+p−N .
Аппроксимация облучающего поля
− важный, но промежуточный этап. Мерилом качества процесса
измерений служит точность восстановления ДН. В отсутствии шумов и приборных
погрешностей эта точность ограничена методической погрешностью, слагаемыми
которой являются: пренебрежение поверхностными волнами (слабый фактор,
заслуживающий лишь упоминания), конечное число N волн пучка и, наконец, использование плоского пучка в
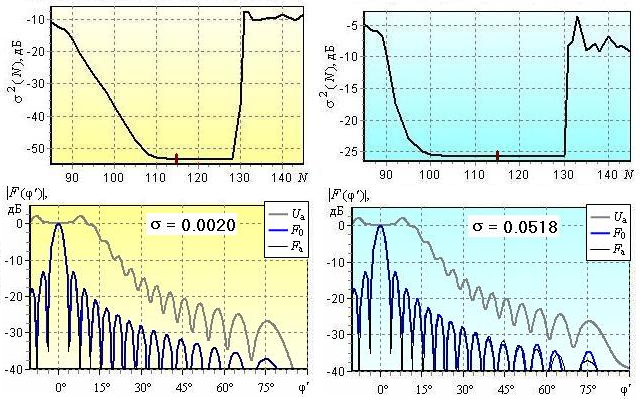
случае сферической облучающей волны. На рис. 8 вверху представлены зависимости
относительной среднеквадратической погрешности 
в децибелах от числа N волн пучка. Здесь 
− восстановленная ДН, Fа(φ') − истинная ДН антенны, 
− измеренная ДН, точнее угловая зависимость принимаемого антенной
сигнала. Песочный фон маркирует вариант цилиндрической волны, изумрудный
− вариант сферической волны.
Внизу на рис.8 представлены ДН при
рациональном выборе N
= 115. В случае цилиндрической волны ДН восстанавливается настолько точно (
< 0,002 = −54дБ), что толстая голубая кривая
и тонкая черная кривая 
сливаются (рис. 8(а)). Принимаемый антенной сигнала представлен толстой серой кривой. Естественно, для сферической волны
(рис. 8(б)) точность скромнее ( = 0,052 = −26дБ).
Но, во-первых, погрешность восстановления ДН заметно меньше погрешности
аппроксимации облучающего поля ( = − 15,5дБ,
рис. 7(б))[3].
Во-вторых, в области ближних боковых лепестков отличие восстановленной ДН от
точных значений не превышает 0.7 дБ, что на практике может быть вполне
приемлемым.
(а) (б)
Рис. 8. Методическая погрешность восстановления ДН при облучении
Шумовые погрешности. Ряд факторов обусловливает погрешности
измерений, носящие случайный характер. Основной среди них − внутренние
шумы измерительного прибора, наличие которых приводит к тому, что каждый отсчет
комплексных амплитуд 
и 
содержит статистически независимые аддитивные
слагаемые 
, реальные и мнимые составляющие которых распределены нормально
с нулевым средним и равной дисперсией 
.
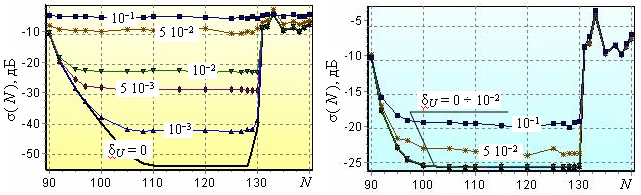
На рис. 9 представлены зависимости среднеквадратичной погрешности
восстановления ДН при различных уровнях нормированного к максимальному значению
принимаемых сигналов и , задаваемых стандартным отклонением 
(корень из дисперсии). Геометрические параметры оставались прежними: La = 15, D = 25. Рис. 9(а) соответствует варианту облучения
цилиндрической волной, рис. 9(б) − облучению сферической волной.
(а) (б)
Рис. 9. Шумовые погрешности восстановления ДН.
Понятно, что при номинальной точности
восстановления на уровне = −50 дБ (рис. 9(а)) даже
чрезвычайно слабые шумы = 10-3, соответствующие
соотношению с/ш = 60дБ, проявляются заметно, а в ситуации умеренной
точности восстановления = −25 дБ (рис. 9(а)) их наличие
не ощутимо вплоть до уровня с/ш = 40дБ (δU < 10-2).
В условиях умеренной точности измерений (при отношении с/ш в интервале от 20дБ до 26дБ), представляющих, по-видимому, наибольший практический интерес, точность восстановления ДН в случае сферической облучающей волны оказывается заметно лучшей, чем в случае облучения цилиндрической волной (естественно, при числе N волн аппроксимирующего пучка из диапазона рациональных значений). Это обусловлено большей устойчивостью соответствующего решения к шумовым погрешностям.
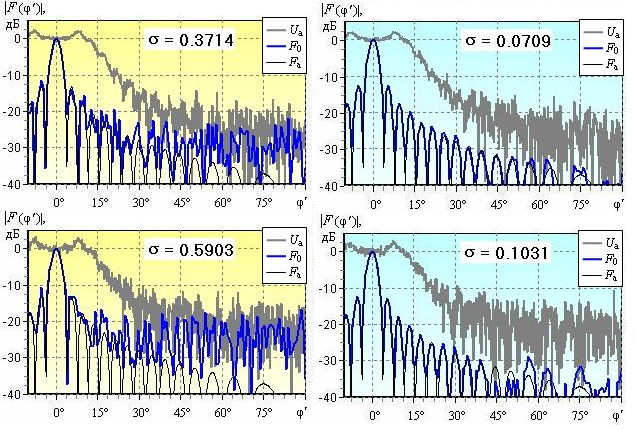
На рис. 10 представлены ДН в случае цилиндрической (а) и сферической (б) облучающей волны при с/ш = 26дБ и с/ш = 20дБ.
(а) (б)
Рис. 10. Восстановление ДН при умеренном уровне шумов:
с/ш=26 дБ (верхний ряд) и с/ш=20 дБ (нижний ряд).
Заметим, что существуют алгоритмические средства уменьшения «чувствительности» решений к случайным погрешностям исходных данных, реализующие классический способ Тихонова и Иванова [6] регуляризации некорректно поставленных задач или статистическую оптимизацию решений (см. [7], полемически изложенный раздел 3 «Optimization versus Regularization»), устраняющую неопределенность выбора значения параметра регуляризации. Очевидно, что с использованием этих программных средств обработки измеренных данных точность восстановления ДН испытуемой антенны при облучении цилиндрической волной и в условиях заметной зашумленности данных будет не хуже, чем в ситуации сферической волны, и единственным достоинством облучения сферической волной останется конструктивная простота вспомогательной антенны.
5. Выводы
Методология восстановления ДН испытуемой антенны, базирующаяся на аппроксимации облучающего поля сходящимся пучком плоских волн, во-первых, наполняет физическим содержанием постулат метода эквивалентной антенны об инвариантности матричного преобразования, связывающего принимаемый зондом или испытуемой антенной сигнала с их ДН. Во-вторых, выявляет факторы, обусловливающие методическую погрешность: пренебрежение поверхностными волнами, ограничения на минимальное и максимальное значение числа волн пучка. В-третьих, условие близости ДН эталонной и ДН испытуемой антенн как гарантии точности восстановления заменяется менее жестким условием близости угловых разрешающих способностей.
Результаты численного моделирования подтверждают возможность достижения приемлемой точности восстановления ДН, когда облучающая волна является сферической, измерения осуществляются в плоскости и поле в рабочей области аппроксимации плоским пучком волн. Более того, получающиеся при этом решения менее чувствительны к шумовым погрешностям измерений.
Литература
1. Бахрах Л.Д., Кременецкий С.Д., Курочкин А.П. Методы измерения параметров излучающих систем в ближней зоне. − Л.: Изд-во «Наука». 1985. 272 с.
2. Плохих С.А., Сазонов Д.М., Щербаков В.И. Восстановление диаграмм направленности антенн методом эталонной антенны по амплифазометрическим измерениям в ближней зоне // Известия вузов. Радиоэлектроника, т. 30. 1987. № 2. С. 59 – 64.
3. Чони Ю.И., Пироженко С.А. Восстановление ДН антенны по результатам измерений в неидеальных условиях // Известия вузов. Радиоэлектроника. т. 35. 1992. №2. С. 43-50.
4. Weixin Zhao. Retrieval of free space radiation patterns through measured data in a non-anechoic environment. PhD dissertation. Syracuse University. USA. December 2013. 165 p. // [Электронный ресурс]. URL: http://surface.syr.edu/cgi/viewcontent.cgi?article=1007&context=etd
5. Кривошеев Ю.В. Измерение характеристик антенн в зоне Френеля на разреженной сетке углов. Канд. диссертация. ФГБОУ ВПО «НИУ «МЭИ». 2014.
6. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач − М.: Наука. Главная редакция физико-математической литературы. 1979. 288 с.
7. Чони Ю.И. Adjoint operator method and its aspects in regard to antenna synthesis. IХ Proceedings of the 2013 IX International Conference on Antenna Theory and Techniques (ICATT). Одесса. Украина. Сентябрь 2013. С. 86-91.
[1] Заметим, что на поверхности S в соответствии с принципом эквивалентных поверхностных токов воспроизводятся касательные компоненты и Eτ (магнитным током), и Hτ (электрическим током). В результате чего внутри S воспроизводится облучающее поле, а вне S поле отсутствует, как если бы внешняя область была идеально проводящей.
[2] Заметим, что для метода эквивалентной антенны [2] неквадратные матрицы СЛАУ недопустимы.
[3] Причину этого можно видеть в том, что антенна является в определенном смысле фильтром слабо чувствительным к «высокочастотным» осциллирующим составляющим пространственного спектра {An}, в то время как в поле пучка E(r,φ) они присутствуют на периферии области S (рис. 6(б)), ухудшая аппроксимацию облучающего поля E0(r,φ).