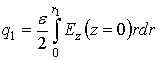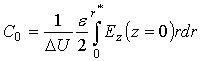УДК 53.083.2
Диагностика подповерхностных неоднородностей среды квазистатическими электрическими полями резонансных СВЧ-зондов
Д. В. Янин, А. Г. Галка, А. И. Смирнов, А. В. Костров
Институт прикладной физики РАН
Статья поступила в редакцию 23 декабря 2015 г.
Аннотация. Работа посвящена развитию метода диагностики подповерхностных неоднородностей диэлектрических сред квазистатическими электрическими полями резонансных СВЧ-зондов. В рамках данного метода источником информации о среде является импеданс электрически малых антенн, расположенных над поверхностью. Для модельных зондов (отрезок двухпроводной линии, краевая емкость цилиндрического конденсатора и т.п.) в рамках борновского приближения разработана схема решения обратной задачи по восстановлению пространственного распределения диэлектрической проницаемости.
Ключевые слова: квазистатическое поле, неоднородности среды, комплексная диэлектрическая проницаемость, электрически-малая антенна, обратная задача.
Abstract: The article is devoted to development of a method of diagnostics of subsurface inhomogeneity of dielectric medium by quasistatic electric fields of resonance microwave probes. Within the limits of this method the information source of mediums characteristic is the impedance of electrically-small antennas located over the mediums surface. The circuit of the decision of an inverse problem is developed for modelling probes (a cut of a two-wire line, edge capacity of the cylindrical capacitor, etc.) within the limits of Born approach on restoration of spatial distribution of a dielectric permittivity.
Key words: quasistatic electric field, medium inhomogeneity, complex dielectric permittivity, electrically-small antennas, inverse problem.
1. Введение
Дистанционная (бесконтактная) диагностика подповерхностных неоднородностей актуальна в различных областях науки и техники (например, в медицине, материаловедении, дефектоскопии, геологоразведке и т.д.). Одним из перспективных методов такой диагностики является резонансная ближнепольная СВЧ-томография, позволяющая визуализировать пространственное распределение электродинамических характеристик (диэлектрической проницаемости и проводимости) исследуемых объектов [1-4]. Основные принципы, на которых базируется этот метод диагностики, можно пояснить следующим образом.
Область среды, находящаяся в ближнем поле электрически малой антенны, оказывает влияние на ее импеданс. Если антенна включена в качестве нагрузки в резонансную систему, то по смещению резонансной частоты и изменению добротности можно судить об электродинамических параметрах среды вблизи антенного устройства. Располагая антенну рядом с поверхностью исследуемого объекта, изменяя ее размеры (глубину зондирования) и местоположение, удается получать информацию о его подповерхностной структуре. Частота зондирующего сигнала, как правило, выбирается из условия, чтобы характерный масштаб локализации квазистатического поля зонда был меньше глубины “скин-слоя” в исследуемой среде. Исходными данными для решения обратной задачи резонансной ближнепольной СВЧ-томографии являются результаты измерения резонансных характеристик диагностической системы при сканировании над поверхностью среды ее измерительной частью, представляющей собой систему электрически малых антенн с разными глубинами зондирования.
В данной статье анализируются особенности постановки обратной задачи ближнепольной СВЧ-томографии на примере резонансных датчиков с зондирующими элементами в виде цилиндрических конденсаторов с металлическим фланцем. Такие датчики успешно применялись нами для изучения изменений в структуре кожного покрова при различных патологиях [5].
2. Резонансные измерительные системы
Измерительная система для исследования подповерхностных
неоднородностей диэлектрической проницаемости представляет собой СВЧ-резонатор
в виде отрезка коаксиальной линии длиной ![]() ~10см, с волновым сопротивлением
~10см, с волновым сопротивлением ![]() =50ом, на одном конце которого находится
нагрузка, включающая в себя зондирующую электрически малую антенну
(измерительную ёмкость Сх), рис. 1. На противоположном конце расположена магнитная
рамка диаметром 0,5 см (для этого центральный проводник коаксиальной линии
замыкается на экран, образуя индуктивную нагрузку
=50ом, на одном конце которого находится
нагрузка, включающая в себя зондирующую электрически малую антенну
(измерительную ёмкость Сх), рис. 1. На противоположном конце расположена магнитная
рамка диаметром 0,5 см (для этого центральный проводник коаксиальной линии
замыкается на экран, образуя индуктивную нагрузку ![]() ).
Возбуждение резонатора и прием его отклика осуществляется при помощи петель
магнитной связи, расположенных вблизи магнитной рамки резонатора.
).
Возбуждение резонатора и прием его отклика осуществляется при помощи петель
магнитной связи, расположенных вблизи магнитной рамки резонатора.
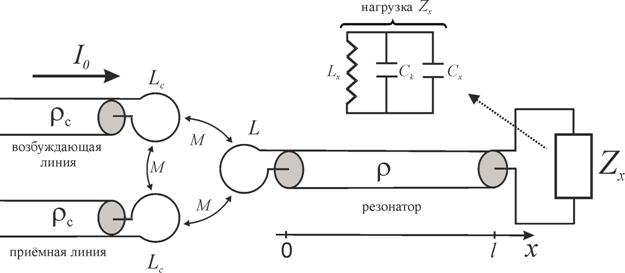
Рис.1. Схема ближнепольной измерительной системы.
|
|
|
Рис.2. Внешний вид резонансной ближнепольной измерительной системы.
Измерительная емкость Сх представляет собой
краевую емкость цилиндрического конденсатора с фторопластовым заполнением. Внешняя
обкладка конденсатора оканчивается плоским металлическим фланцем, рис.2 (![]() – емкость цилиндрического конденсатора
без учета краевого эффекта). Длина конденсатора составляла 5мм, радиус
внутреннего проводника – 3мм. Глубина зондирования системы определяется
расстоянием между внешней и внутренней обкладками конденсатора, которое
варьировалось в пределах от 0,25мм до 2мм. Для сильноконтрастных объектов такие
зазоры обеспечивали глубины зондирования от 0.1мм до 1мм. Коррекция резонансной
характеристики системы для конкретной исследуемой среды осуществляется при
помощи индуктивности Lx, включённой параллельно с Сх.
Торец цилиндрического конденсатора с плоским металлическим фланцем
прикладывается к поверхности исследуемой среды. Наличие вещества в области
краевого квазистатического поля цилиндрической емкости приводит к изменению
резонансной частоты и добротности системы. Собственная резонансная частота измерительных
систем
– емкость цилиндрического конденсатора
без учета краевого эффекта). Длина конденсатора составляла 5мм, радиус
внутреннего проводника – 3мм. Глубина зондирования системы определяется
расстоянием между внешней и внутренней обкладками конденсатора, которое
варьировалось в пределах от 0,25мм до 2мм. Для сильноконтрастных объектов такие
зазоры обеспечивали глубины зондирования от 0.1мм до 1мм. Коррекция резонансной
характеристики системы для конкретной исследуемой среды осуществляется при
помощи индуктивности Lx, включённой параллельно с Сх.
Торец цилиндрического конденсатора с плоским металлическим фланцем
прикладывается к поверхности исследуемой среды. Наличие вещества в области
краевого квазистатического поля цилиндрической емкости приводит к изменению
резонансной частоты и добротности системы. Собственная резонансная частота измерительных
систем ![]() составляла порядка 800 МГц, добротность
составляла порядка 800 МГц, добротность ![]() ~ 150.
~ 150.
Согласно [3,4], резонансная частота ![]() и амплитуда сигнала
и амплитуда сигнала ![]() в максимуме резонансной кривой датчика определяется величиной измерительной
емкости в соответствии со следующими выражениями:
в максимуме резонансной кривой датчика определяется величиной измерительной
емкости в соответствии со следующими выражениями:
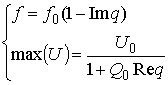 (1)
(1)
где
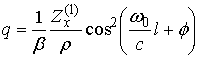 (2)
(2)
 (3)
(3)
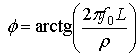 (4)
(4)
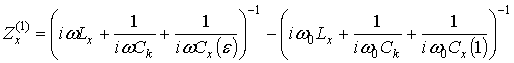 (5)
(5)
Таким образом, выражения (1)–(5) позволяют определить
величину измерительной емкости ![]() при контакте ее с
поверхностью неоднородной среды по экспериментально найденным
при контакте ее с
поверхностью неоднородной среды по экспериментально найденным ![]() и
и ![]() .
.
Значения ![]() для измерительных
емкостей с разным масштабом локализации зондирующего поля (с разными зазорами
между центральным и внешним проводниками цилиндрического конденсатора) являются
исходными данными для решения обратной задачи по восстановлению
пространственного распределения электродинамических характеристик среды.
для измерительных
емкостей с разным масштабом локализации зондирующего поля (с разными зазорами
между центральным и внешним проводниками цилиндрического конденсатора) являются
исходными данными для решения обратной задачи по восстановлению
пространственного распределения электродинамических характеристик среды.
3. Краевая емкость цилиндрического конденсатора
Рассмотрим цилиндрический конденсатор в виде двух проводящих коаксиальных цилиндра радиусами r1 и r2 (r2 > r1). Внешняя обкладка конденсатора оканчивается бесконечным металлическим фланцем, рис.3.
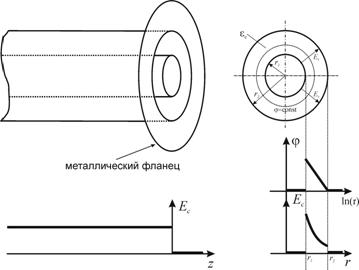
Рис.3. Цилиндрический конденсатор с
бесконечным металлическим фланцем.
Распределение электрического поля и его
потенциала без учета краевого эффекта
Пространство между обкладками заполнено средой с
диэлектрической проницаемостью ![]() . Распределение
электрического поля в такой системе без учёта краевых эффектов на торцах цилиндров
хорошо известно. В плоскости поперечного сечения конденсатора радиальные линии
представляют собой силовые линии электрического поля, концентрические
окружности – линии равного потенциала. Электрическое поле вне конденсатора
равно нулю.
. Распределение
электрического поля в такой системе без учёта краевых эффектов на торцах цилиндров
хорошо известно. В плоскости поперечного сечения конденсатора радиальные линии
представляют собой силовые линии электрического поля, концентрические
окружности – линии равного потенциала. Электрическое поле вне конденсатора
равно нулю.
Если ![]() –
поверхностная плотность заряда на центральном цилиндре
–
поверхностная плотность заряда на центральном цилиндре ![]() ,
разность потенциалов
,
разность потенциалов ![]() между обкладками и радиальное
электрическое поле
между обкладками и радиальное
электрическое поле ![]() выражаются в следующем виде:
выражаются в следующем виде:
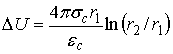 , (6)
, (6)
Ёмкость на единицу длины конденсатора определяется выражением:
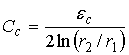 (8)
(8)
Учёт краевого эффекта приводит к изменению распределения поля в окрестности торца конденсатора. Во-первых, наличие электрического заряда на металлическом фланце и торце центрального проводника приводит к появлению электрического поля вне конденсатора. Во-вторых, внутри конденсатора наблюдается усиление поля вблизи торца с увеличением поверхностной плотности заряда на внешней и центральной обкладке и появление аксиальной компоненты электрического поля.
Для того, чтобы исключить взаимное влияние торцов конденсатора друг на друга, будем предполагать, что длина цилиндрического конденсатора неограниченна. Именно такая модель наиболее приближена к случаю, когда зазор между обкладками существенно меньше их длины.
Краевое электрическое поле ![]() цилиндрического
конденсатора при контакте с поверхностью неоднородного полупространства с
диэлектрической проницаемостью
цилиндрического
конденсатора при контакте с поверхностью неоднородного полупространства с
диэлектрической проницаемостью ![]() описывается уравнением
Пуассона:
описывается уравнением
Пуассона:
c граничным условием в плоскости торца
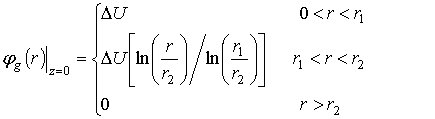 (10)
(10)
Если комплексную диэлектрической проницаемость среды ![]() можно представить в виде малого
отклонения
можно представить в виде малого
отклонения ![]() , занимающего конечную область в
полупространстве
, занимающего конечную область в
полупространстве ![]() , от некоторого постоянного
значения
, от некоторого постоянного
значения ![]() в остальной части этого пространства:
в остальной части этого пространства:
![]() (11)
(11)
решение задачи (9)-(11) можно искать методом теории возмущений.
Потенциал ![]() , электрическое поле
, электрическое поле ![]() и поверхностную плотность заряда
и поверхностную плотность заряда ![]() на торце центрального проводника
представим в виде невозмущенных значений
на торце центрального проводника
представим в виде невозмущенных значений ![]() ,
, ![]() и
и ![]() ,
соответствующих однородной среде и малых добавок
,
соответствующих однородной среде и малых добавок ![]() ,
, ![]() и
и ![]() ,
связанных с малой неоднородной компонентой комплексной диэлектрической
проницаемости среды
,
связанных с малой неоднородной компонентой комплексной диэлектрической
проницаемости среды ![]() .
.
![]() (12)
(12)
В нулевом приближении (среда однородная) электрическое поле вне конденсатора описывается уравнением:
![]()
![]() (13)
(13)
с граничным условием (9). Решение этой задачи будем искать альтернативным способом. Краевые поля цилиндрического конденсатора с бесконечным металлическим фланцем могут быть вычислены как поля плоского кольцевого магнитного тока. Действительно, без учёта краевого эффекта на торце конденсатора, в плоскости z=0 имеется скачок радиального электрического поля.
![]() (14)
(14)
В соответствии с граничным условием (14) данному разрывному
полю соответствует поверхностный кольцевой магнитный ток ![]() (
(![]() -
единичный орт вдоль азимутального направления), текущий в плоскости раскрыва
между центральным и внешним проводниками цилиндрической емкости, рис. 4.
-
единичный орт вдоль азимутального направления), текущий в плоскости раскрыва
между центральным и внешним проводниками цилиндрической емкости, рис. 4.
 (15)
(15)
Стоит отметить, что таким путем, в частности, решаются задачи о возбуждении электромагнитного поля в волноводах щелями и другими отверстиями, прорезанными в их стенках.
Магнитный векторный потенциал ![]() ,
создаваемый током
,
создаваемый током ![]() , в случае однородной среды вне
конденсатора равен:
, в случае однородной среды вне
конденсатора равен:
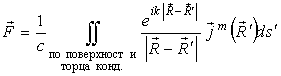 (16)
(16)
(штрихом отмечены координаты источника).
Величина ![]() , как легко установить
из рис. 4, равна:
, как легко установить
из рис. 4, равна: ![]() . Электрическое поле
. Электрическое поле ![]() выражается через магнитный векторный
потенциал
выражается через магнитный векторный
потенциал ![]() следующим образом:
следующим образом:
![]() .
.
При вычислении вектора ![]() рассмотрим
элементарную площадку
рассмотрим
элементарную площадку ![]() на плоском кольце. Если сначала
проводить интегрирование по
на плоском кольце. Если сначала
проводить интегрирование по ![]() , а затем по
, а затем по ![]() , то плоское кольцо разбивается на систему
магнитных кольцевых токов шириной
, то плоское кольцо разбивается на систему
магнитных кольцевых токов шириной ![]() каждый. В силу осевой
симметрии задачи (все величины не зависят от азимутального угла) можно без
потери общности выбрать точку наблюдения в плоскости
каждый. В силу осевой
симметрии задачи (все величины не зависят от азимутального угла) можно без
потери общности выбрать точку наблюдения в плоскости ![]() (при
этом
(при
этом ![]() ). При вычислении вклада
). При вычислении вклада ![]() в интеграл
в интеграл ![]() введен
множитель
введен
множитель ![]() , а интегрирование по
, а интегрирование по ![]() проводится от 0 до
проводится от 0 до ![]() . В результате, магнитный векторный
потенциал принимает вид:
. В результате, магнитный векторный
потенциал принимает вид:
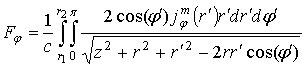 (17)
(17)
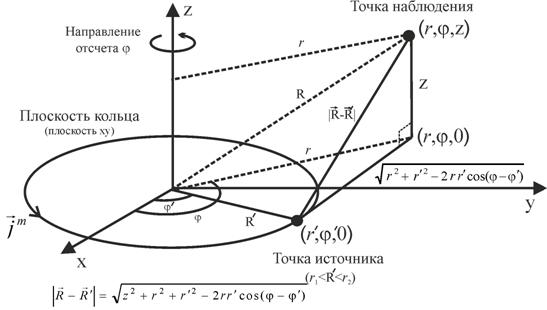
Рис.4. Расположение источника и точки наблюдения для кольцевого магнитного тока.
Составляющие поля ![]() и
и ![]() находятся путём дифференцирования
находятся путём дифференцирования ![]() , и выражаются следующими формулами:
, и выражаются следующими формулами:
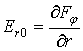 (19)
(19)
Выполнение процедуры дифференцирования позволяет получить
выражения для ![]() и
и ![]() в виде
двукратных интегралов. Проведя интегрирование по переменной
в виде
двукратных интегралов. Проведя интегрирование по переменной ![]() можно свести интегралы к однократным:
можно свести интегралы к однократным:
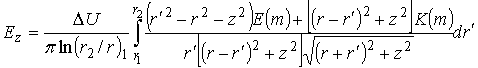 (21)
(21)
где ![]() и
и ![]() полные
эллиптические интегралы Лежандра первого и второго рода соответственно.
полные
эллиптические интегралы Лежандра первого и второго рода соответственно.
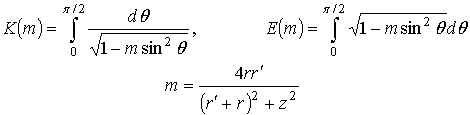 (22)
(22)
![]() и
и ![]() представляются
в виде степенного ряда:
представляются
в виде степенного ряда:
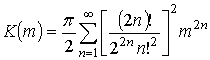 ,
, 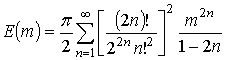 (23)
(23)
В соответствии с этим, полные эллиптические интегралы можно с заданной точностью аппроксимировать полиномиальной зависимостью. Это обстоятельство позволяет сократить вычислительное время при расчете полей с помощью (20) и (21) по сравнению с численным интегрированием двукратных интегралов, соответствующих (18)–(19).
На рис. 5-8 представлен
численный расчёт ![]() и
и ![]() компонент
электрического поля вне цилиндрического конденсатора с бесконечным
металлическим фланцем. Радиус внутреннего проводника составлял r1=3мм,
радиус внешнего проводника – r2=3.5мм. Видно, что в плоскости
раскрыва радиальная компонента поля
компонент
электрического поля вне цилиндрического конденсатора с бесконечным
металлическим фланцем. Радиус внутреннего проводника составлял r1=3мм,
радиус внешнего проводника – r2=3.5мм. Видно, что в плоскости
раскрыва радиальная компонента поля ![]() отлична от нуля только
в зазоре между внешним и внутренним проводником конденсатора. По величине
отлична от нуля только
в зазоре между внешним и внутренним проводником конденсатора. По величине ![]() совпадает с полем
совпадает с полем ![]() в
конденсаторе без учёта краевого эффекта.
в
конденсаторе без учёта краевого эффекта. ![]() компонента
монотонно растет по координате r, достигает максимума при r=r1,
затем уменьшается, меняет знак и достигает минимума при r=r2.
При r=r* (r1<r*<r2)
компонента
монотонно растет по координате r, достигает максимума при r=r1,
затем уменьшается, меняет знак и достигает минимума при r=r2.
При r=r* (r1<r*<r2) ![]() обращается в нуль. По мере удаления от
плоскости раскрыва, электрическое поле спадает с характерным масштабом порядка
зазора между внутренней и внешней обкладками конденсатора.
обращается в нуль. По мере удаления от
плоскости раскрыва, электрическое поле спадает с характерным масштабом порядка
зазора между внутренней и внешней обкладками конденсатора.

Рис. 5. Радиальное
распределение ![]() (а) и
(а) и ![]() (б)
компонент электрического поля в плоскости раскрыва
(б)
компонент электрического поля в плоскости раскрыва
цилиндрического конденсатора
с бесконечным металлическим фланцем. (r1=3мм, r2=3,5мм)
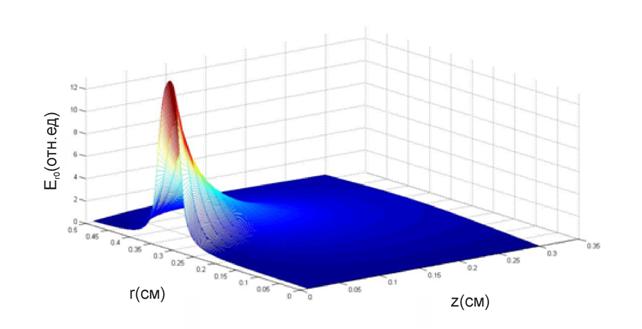
Рис.6. Пространственная структура ![]() компоненты краевого электрического поля
компоненты краевого электрического поля
цилиндрического конденсатора с бесконечным металлическим фланцем (r1=3мм,
r2=3,5мм)
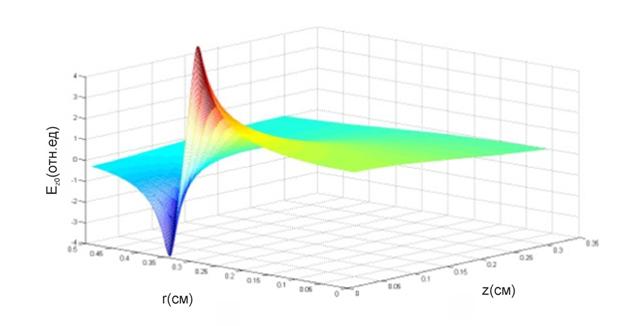
Рис.7. Пространственная структура ![]() компоненты краевого электрического поля
компоненты краевого электрического поля
цилиндрического конденсатора с бесконечным металлическим фланцем (r1=3мм,
r2=3,5мм)

Рис.8. Пространственная структура модуля краевого
электрического поля
цилиндрического конденсатора с бесконечным металлическим
фланцем (r1=3мм, r2=3,5мм)
Поверхностная плотность заряда ![]() на
торце центрального проводника определяется в соответствии с граничным условием
на металле:
на
торце центрального проводника определяется в соответствии с граничным условием
на металле:
![]() (24)
(24)
где ![]() – аксиальная компонента вектора индукции
электрического поля. Если ε – диэлектрическая проницаемость среды вне
конденсатора (считается, что среда однородная), то
– аксиальная компонента вектора индукции
электрического поля. Если ε – диэлектрическая проницаемость среды вне
конденсатора (считается, что среда однородная), то ![]() .
.
Полный заряд ![]() на торце центральной
жилы определяется путём интегрирования
на торце центральной
жилы определяется путём интегрирования ![]() по
соответствующей ему поверхности:
по
соответствующей ему поверхности:
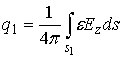 (25)
(25)
(![]() – поверхность торца центральной жилы).
– поверхность торца центральной жилы).
В силу азимутальной симметрии, имеем:
Внутри конденсатора электрическое поле можно представить в
виде суперпозиции однородного радиального электрического поля ![]() , соответствующего (7), как для случая
безграничных коаксиальных проводников и поправки
, соответствующего (7), как для случая
безграничных коаксиальных проводников и поправки ![]() ,
обусловленной краевым эффектом. В первом приближении силовые линии поля
,
обусловленной краевым эффектом. В первом приближении силовые линии поля ![]() являются продолжением аксиального поля
являются продолжением аксиального поля ![]() в плоскости раскрыва внутрь конденсатора:
линии поля
в плоскости раскрыва внутрь конденсатора:
линии поля ![]() , имеющие начало на поверхности
центрального проводника, соответствуют полю
, имеющие начало на поверхности
центрального проводника, соответствуют полю ![]() при r1<r<r*,
линии
при r1<r<r*,
линии ![]() , оканчивающиеся на поверхности внешнего
цилиндра, соответствуют полю
, оканчивающиеся на поверхности внешнего
цилиндра, соответствуют полю ![]() при r*<r<r2.
Качественно структура силовых линий
при r*<r<r2.
Качественно структура силовых линий ![]() представлена на рис. 9.
Пунктирной линией показана “нулевая” силовая линия, упирающаяся в точку r*
в плоскости торца. Нахождение аналитического выражения для поля
представлена на рис. 9.
Пунктирной линией показана “нулевая” силовая линия, упирающаяся в точку r*
в плоскости торца. Нахождение аналитического выражения для поля ![]() представляет собой довольно сложную
задачу и в рамках данной работы не проводится.
представляет собой довольно сложную
задачу и в рамках данной работы не проводится.
Полю ![]() соответствует дополнительная
плотность заряда
соответствует дополнительная
плотность заряда ![]() на поверхности центрального
проводника внутри конденсатора и, соответственно, дополнительный заряд
на поверхности центрального
проводника внутри конденсатора и, соответственно, дополнительный заряд ![]() :
:
где ![]() – боковая поверхность центрального
проводника.
– боковая поверхность центрального
проводника.
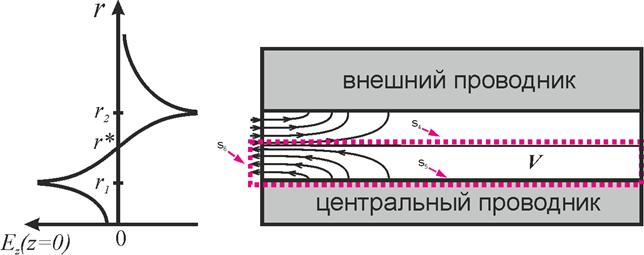
Рис.9. Справа показана
качественная картина силовых линий электрического поля внутри коаксиала,
обусловленного краевым эффектом. Слева иллюстрируется Ez
компонента электрического поля в плоскости раскрыва.
Для нахождения ![]() рассмотрим область
рассмотрим область ![]() внутри конденсатора, содержащую силовые
линии поля
внутри конденсатора, содержащую силовые
линии поля ![]() , оканчивающиеся на центральном
проводнике, рис.9. Трубчатая поверхность
, оканчивающиеся на центральном
проводнике, рис.9. Трубчатая поверхность ![]() ,
ограничивающая область V, состоит из поверхности
,
ограничивающая область V, состоит из поверхности ![]() ,
соответствующей “нулевым” силовым линиям поля
,
соответствующей “нулевым” силовым линиям поля ![]() ,
поверхностью
,
поверхностью ![]() центрального проводника и кольцом
центрального проводника и кольцом ![]() в плоскости раскрыва с внутренним
радиусом r1 и внешним r*.
в плоскости раскрыва с внутренним
радиусом r1 и внешним r*.
Для поверхности ![]() применим теорему
Гаусса. Поскольку в области V отсутствуют заряды, поток вектора индукции
поля
применим теорему
Гаусса. Поскольку в области V отсутствуют заряды, поток вектора индукции
поля ![]() через поверхность
через поверхность ![]() равен
нулю:
равен
нулю:
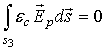 (28)
(28)
В плоскости торца, в силу непрерывности нормальной компоненты
индукции электрического поля получаем связь между ![]() и
полем вне конденсатора:
и
полем вне конденсатора:
![]() (29)
(29)
На поверхности центрального проводника имеем:
![]() (30)
(30)
Поток поля ![]() через поверхность
через поверхность ![]() равен нулю.
равен нулю.
В соответствии с (29) и (30), учитывая азимутальную симметрию, перепишем (28) в виде:
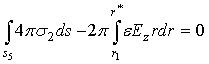 (31)
(31)
Откуда с учётом (27) получаем
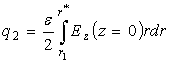 (32)
(32)
Таким образом, учёт краевого эффекта приводит к появлению
дополнительного заряда на поверхности центрального проводника и на его торце,
который определяет краевую ёмкость ![]() цилиндрического
конденсатора:
цилиндрического
конденсатора:
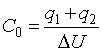 (33)
(33)
Учитывая (26) и (32), получаем:
При наличии неоднородной составляющей комплексной
диэлектрической проницаемости среды ![]() , в первом порядке
теории возмущений для потенциала
, в первом порядке
теории возмущений для потенциала ![]() имеем:
имеем:
![]() (35)
(35)
с граничным условием
![]() (36)
(36)
Правую часть уравнения (35) можно рассматривать в виде объёмной
плотности заряда ![]() в полупространстве
в полупространстве ![]() .
.
Плоскость торца конденсатора является эквипотенциальной
поверхностью, которую можно заметализировать, и для нахождения ![]() воспользоваться методом электрических
изображений.
воспользоваться методом электрических
изображений.
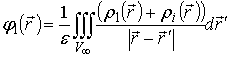 (37)
(37)
![]() – область, соответствующая безграничному
пространству, занятого исследуемой средой,
– область, соответствующая безграничному
пространству, занятого исследуемой средой, ![]() –
объемная плотность зарядов изображения.
–
объемная плотность зарядов изображения.
Поверхностная плотность заряда ![]() в
плоскости торца связана с
в
плоскости торца связана с ![]() соотношением
соотношением
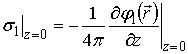 (38)
(38)
Перейдя в интеграле (37) к цилиндрической системе координат,
с учётом зеркальной симметрии объёмной плотности заряда относительно плоскости ![]() получаем:
получаем:
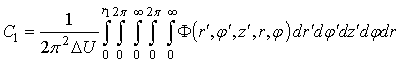 (39)
(39)
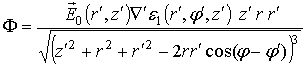 (40)
(40)
В результате, согласно (34), (39) и (40), краевая ёмкость
цилиндрического конденсатора ![]() в случае неоднородной
среды определяется следующим соотношением:
в случае неоднородной
среды определяется следующим соотношением:
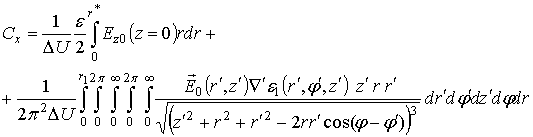 (41)
(41)
Выражение (41) связывает зондирующую краевую емкость цилиндрического конденсатора с металлическим фланцем с неоднородной в пространстве комплексной диэлектрической проницаемости среды. Для системы резонансных датчиков с разными глубинами зондирования совокупность соответствующих выражений (41) представляет собой систему интегральных уравнений для нахождения электродинамических параметров неоднородного полупространства.
4. Выводы
Таким образом, в работе изучены особенности постановки обратной задачи резонансной ближнепольной СВЧ-томографии на примере ближнепольных зондов в виде краевой емкости цилиндрического конденсатора с металлическим фланцем. При такой диагностике источником информации о подповерхностной структуре среды являются результаты измерения импеданса набора зондов с разными масштабами локализации квазистатического электрического поля. В рамках борновского приближения получено интегральное уравнение, связывающее емкость зонда с пространственным распределением комплексной диэлектрической проницаемости неоднородного полупространства.
Работа выполнена при поддержке РФФИ, грант № 15-47-02294-р_поволжье_а, грант № 16-02-00823.
Литература
1. М.И. Эпов, В.Л. Миронов, П.П. Бобров, И.В. Савин, А.В. Репин. Исследование диэлектрической проницаемости нефтесодержащих пород в диапазоне частот 0.05—16 ГГц // Геология и геофизика, 2009, т. 50, № 5. С. 613—618.
2. T Sunaga, H Ikehira, S Furukawa, H Shinkai, H Kobayashi, Y Matsumoto, E Yoshitome, T Obata, S Tanada, H Murata and Y Sasaki. Measurement of the electrical properties of human skin and the variation among subjects with certain skin conditions // Physics in Medicine and Biology. Volume 47, Number 1, 7 January 2002. P. N11-N15.7.
3. Д.В. Янин, А.В. Костров, А.И. Смирнов, М.Е. Гущин, С.В. Коробков, А.В. Стриковский, В.И. Гундорин, В.В. Назаров, М.В. Стародубцев. Диагностика параметров плазмы атмосферного давления методом ближнепольного СВЧ-зондирования // ЖТФ, 2012, том 82, вып. 4. С. 42-51
4. Янин Д.В., Галка А.Г., Костров А.В., Смирнов А.И., Стриковский А.В., Кузнецов И.В. Подповерхностная диагностика квазиодномерных неоднородностей методом резонансного ближнепольного СВЧ-зондирования // Известия вузов. Радиофизика. 2014. Т.57. №1. С. 35-47.
5. Д.В. Янин, А.Г. Галка, А.И. Смирнов, А.В. Костров, А.В. Стриковский. Резонансная ближнепольная СВЧ-диагностика неоднородных сред // Успехи прикладной физики. 2014. Т.2. №6. С. 555-570.