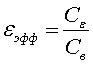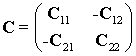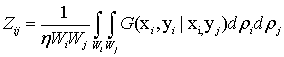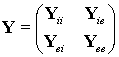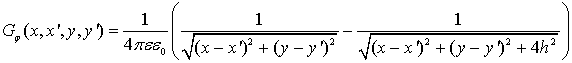"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 2016

оглавление

Моделирование электромагнитных связей между планарными резонаторами

 

Д. В. Денисенко, В. В. Радченко

ФГУП «ЦНИРТИ им. академика А.И. Берга

 

Статья поступила в редакцию 22 декабря 2015 г.

 

Аннотация.  В работе рассматривается метод моделирования характеристик передачи связанных планарных резонаторов произвольной формы. Используются волноводная модель резонатора, квазистатическое приближение, методы сегментации и моментов. Разработанный метод ориентирован на применение в задачах параметрической оптимизации широкого круга планарных СВЧ устройств.

Ключевые слова: планарные резонаторы, квазистатическое моделирование, метод сегментации, волноводная модель.

Abstract. This paper discusses the method for modeling the characteristics of the transmission coupled planar resonators of arbitrary shape. Cavity model of planar resonator, method of segmentation, method of moments and quasi-static approximations are used. The developed method is applied to the problems of parametric optimization of a wide range of planar microwave devices.

Key words:  planar resonator, quasi-static, segmentation method, cavity model, coupled lines.

1.      Введение

Планарные устройства СВЧ представляют собой композицию из отрезков полосковых линий передачи (ПЛП) и неоднородностей, которые связаны между собой по электромагнитному полю. В процессе разработки таких устройств находят широкое применение системы автоматизированного проектирования (САПР), которые позволяют прогнозировать характеристики реального устройства по заданной модели. В них реализованы различные методы численного анализа, которые позволяют решить электромагнитную задачу в строгой постановке или используют упрощенные модели с целью сокращения времени расчета.

 На начальных этапах разработки большинства СВЧ устройств необходима оптимизация геометрических размеров линий и неоднородностей путем перебора множества вариантов с целью получения заданной характеристики. Время однократного расчета задачи методами полного электромагнитного анализа измеряется десятками минут в зависимости от сложности задачи и требуемой точности моделирования. Это не позволяет перебрать нужное количество вариантов за приемлемое время. С этой задачей позволяют справиться приближенные методы квазистатического анализа и декомпозиции. При таком подходе устройство разбивается на отдельные элементы, которые заменяются эквивалентными многополюсниками, соединенными в общую схему. За пределами многополюсников электромагнитные связи между отдельными элементами обычно полагают отсутствующими. Если внутренние электромагнитные связи существенно влияют на характеристики устройства, они могут быть смоделированы отдельно и добавлены в цепь в качестве отдельного многополюсника.

 

5

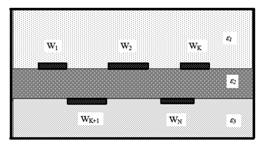
Рис. 1. Поперечное сечение экранированной многосвязной полосковой структуры

 

В квазистатическом приближении предполагается, что в элементах на основе ПЛП распространяются только TEM-волны. Это позволяет рассчитать характеристики передачи многополюсников методами электростатического анализа [1] на нулевой частоте с последующим распространением на СВЧ диапазон. Для квазистатического расчета электромагнитных связей между планарными элементами обычно используются модели связанных линий, которые справедливы в предположении, что они имеют бесконечную длину, а их ширина не может существенно превышать толщину диэлектрической подложки. Внешний вид поперечного сечения такой модели показан на рис.1.

Погонные параметры планарной структуры [2] рассчитываются в поперечном сечении, что означает, что  продольное электрическое поле однородно, все полосковые линии одинаковой длины, параллельны друг другу и постоянной ширины. Для определения характеристики передачи такой структуры используются телеграфные уравнения. В случае, когда длина полосковых линий сравнима с их шириной, ошибка приближения не позволяет получить адекватные результаты из-за пренебрежения неоднородностями поля вблизи краев разомкнутых концов. В моделях зазоров между открытыми концами линий, напротив, их ширина не должна сильно превышать величину толщины диэлектрической подложки. В общем случае отрезки связанных линий могут иметь разную длину. Все это вносит существенные ограничения на возможности оптимизации устройств с наличием электромагнитных связей между более сложными элементами. Другой подход предполагает определение параметров матриц рассеяния отдельных элементов и дополнительных матриц связей, которые моделируют эффекты излучения и приема сигнала [3], однако с точки зрения корректности и эффективности, каждая задача в этом случае требует индивидуального подхода.

Целью работы является разработка метода квазистатического моделирования и его реализация в виде программы ЭВМ, которая предназначена для сокращения времени решения задачи параметрической оптимизации планарных неоднородностей с учетом электромагнитных связей между элементами, размеры и взаимное расположение которых не укладываются в допущения существующих моделей.

2.      Модель связанных резонаторов

Рассмотрим неоднородность в виде двух планарных резонаторов произвольной формы в многослойном диэлектрике, как показано на рис.2. Чтобы определить характеристику передачи такого элемента, будем рассчитывать многомодовые матрицы параметров каждого из резонаторов независимо друг от друга, затем определим распределение частичных емкостей для восстановления электромагнитных связей между различными участками резонаторов. В процессе расчета нам будет необходимо определить эффективную диэлектрическую проницаемость среды, которая может быть найдена в квазистатическом приближении как отношение его собственной емкости при заполнении диэлектриком к собственной емкости в воздушном заполнении [4]:

 

(1)

 

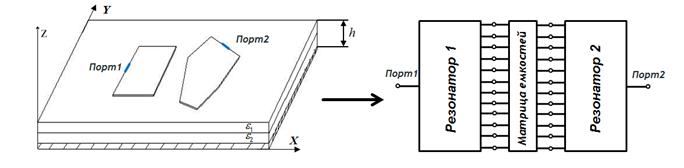
Рис. 2. Планарные резонаторы на диэлектрической подложке

 

Емкости резонаторов и матрицу связей между их отдельными частями, а также собственные частичные емкости можно получить на нулевой частоте из решения уравнения Пуассона методом моментов. Решение выполняется для среды, скалярная функция Грина которой может быть найдена аналитически. Интегральное уравнение для потенциала на поверхности S проводника запишется как:

,

(2)

где  - поверхностная плотность заряда,  - функция Грина уравнения Лапласа, r – точка наблюдения, r’ – точка источника возбуждения.

Разбиение поверхности проводников на N конечных элементов (КЭ) приводит к симметричной матрице связей между зарядами и потенциалами размера NxN. Решение интегрального уравнения с заданной разностью потенциалов между проводниками даст информацию о распределении поверхностного заряда по проводникам, зная которое можно определить параллельно распределенные взаимные частичные емкости. В случае с кусочно-постоянной аппроксимацией плотности заряда, обращение матрицы коэффициентов даст полную матрицу частичных емкостей для системы проводников [5], представляющих собой КЭ:

,

(3)

где  и  – матрицы собственных частичных емкостей для КЭ каждого из проводников, а  и  – матрицы связей между КЭ отдельных резонаторов. Сумма всех элементов матрицы  есть собственная емкость первого проводника, которая необходима для использования в формуле (1). Аналогично емкость второго проводника находится из суммы всех элементов . Связь между резонаторами по электромагнитному полю может быть записана в виде матрицы проводимостей , где , а f – частота. Для составления полной матрицы проводимостей системы двух резонаторов, нужно найти Y11 и Y22 для выводов по периметру резонаторов путем инвертирования соответствующих матриц Z - параметров.

Для структур с относительно тонкими диэлектрическими подложками по сравнению с размерами резонаторов можно считать, что вся энергия электрического поля сосредоточена в диэлектрике между проводником и проводящей плоскостью, силовые линии электрического поля E направлены строго вдоль оси z, что эквивалентно наличию магнитных стенок по периметру проводника. В таком приближении каждый резонатор можно представить в виде эквивалентного многополюсника с произвольным количеством выводов, матрицы параметров которого можно получить, используя эквивалентную волноводную модель планарной линии [6]. Волновое уравнение для потенциала V на поверхности проводника записывается в виде:

,

(4)

где Jz  – плотность вертикального фиктивного тока в сечении вывода, d – толщина подложки,

k – волновое число,  – магнитная постоянная.

Решение этого уравнения может быть выражено через функцию Грина  области проводника:

,

(5)


где- координата в произвольной точке в области резонатора, а - точка источника возбуждения, D – область проводника

Если ширина выводов достаточно мала, то плотность тока в них можно считать распределенной равномерно, и тогда при помощи (5) элементы матрицы Z-параметров находятся как

,

(6)

 

где Wi  - ширина i -го вывода, – расстояния между точками выводов,  - коэффициент, который показывает, какая часть полного фиктивного тока вытекает из вывода на заземляющую плоскость, так = 2 для симметричной полосковой линии (СПЛ) и можно считать = 1 для микрополосковой линии (МПЛ).

Функции Грина планарных элементов известны только для простых областей, таких как прямоугольник, окружность, равносторонний и прямоугольный равнобедренный треугольники, сектор окружности [4]. Матрицы Z-параметров более сложных элементов могут быть получены путем сложения матриц простых элементов. Функции Грина вышеперечисленных элементов представляют собой двойные ряды, поскольку находятся из разложения решения уравнения по собственным функциям. В выражении для прямоугольного элемента, одна из сумм находится аналитически, что существенно сокращает объем необходимых вычислений и делает прямоугольные элементы наиболее привлекательными для практического применения с точки зрения затрат машинного времени. Интегралы в формуле (6) берутся аналитически для прямоугольных элементов, окружности и сектора окружности, что избавляет от необходимости численного интегрирования. Если же форма не может быть получена путем комбинирования простых элементов, то возможно нахождение матрицы Z-параметров путем численного решения интегрального уравнения с использованием двумерной функции Грина свободного пространства [3].

Данная модель не учитывает эффекта увеличения электрической длины линии из-за краевой емкости. Он может быть компенсирован сдвигом магнитных стенок на некоторое расстояние от края проводника, что эквивалентно замене реальных геометрических размеров на эффективные, для которых в частных случаях существуют способы оценки. Также возможно заземление краев проводника через соответствующие частичные краевые емкости, что также дает необходимый эффект.

     Чтобы соединить неиспользуемые выводы между собой и определить матрицу соответствующего многополюсника, общая матрица Y параметров представляется в виде:

,

(7)

где e – индексы, которые соответствуют выбранным внешним выводам, а i – индексы внутренних соединений [7]. Тогда

(8)

 

3.      Численная реализация и анализ результатов

Для проведения численного эксперимента была написана многопоточная программа на языке программирования C++ с использованием оптимизированных библиотек высокопроизводительных вычислений BLAS для операций с матрицами и LAPACK для решения систем алгебраических линейных уравнений (СЛАУ). С целью упрощения процесса отладки программы и проверки работоспособности предложенной модели, была рассмотрена задача определения матрицы рассеяния двух прямоугольных бесконечно тонких проводников с размерами длины и ширины одного порядка и расположенных на высоте h над проводящей плоскостью. Диэлектрическое заполнение со всех сторон считается однородным с диэлектрической проницаемостью , экран отсутствует. Оба резонатора разбивались равномерно на одинаковое количество выводов по периметру и одинаковое количество прямоугольных элементов, по которым плотность заряда аппроксимировалась кусочно – постоянной функцией.

Трехмерную функцию Грина уравнения Лапласа для проводящей плоскости можно записать в виде:

(9)

где x, y – координаты точки наблюдения, x’, y’ – координаты точки источников возбуждения,

– электрическая постоянная.

Элементы матрицы СЛАУ вычисляются следующим образом:

,

(10)

 

где индекс i соответствует КЭ с точкой наблюдения в ее центре (x, y), а j – КЭ, по координатам которой производится интегрирование.

В рассматриваемой задаче эти интегралы берутся аналитически и высокая точность коэффициентов СЛАУ гарантирована. Для более сложных представлений функций Грина существуют специальные численно-аналитические методы интегрирования функций с особенностями, которые позволяют существенно снизить объем необходимых вычислений.

Из полученной методом моментов матрицы частичных емкостей  были выбраны элементы краевых и взаимных емкостей, которые дают наибольший вклад, и сгруппированы по соответствию заданным входам и выходам эквивалентного многополюсника. Затем формировалась общая матрица проводимостей. Отметим, что не существует универсального алгоритма для распределения по выводам емкостных связей, которые соответствуют элементам из внутренних областей резонаторов, поэтому в представленной реализации брались усредненные величины так, чтобы суммарная взаимная емкостная связь оказалась полной. Краевые собственные частичные емкости присоединялись к выводам и заземлялись.

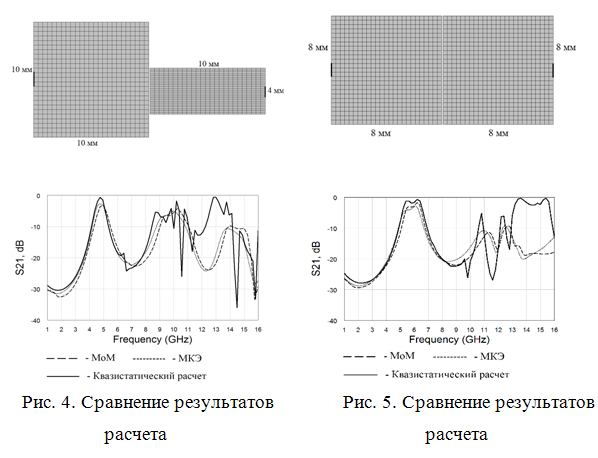
Для демонстрации работы программы были рассчитаны две конфигурации из близкорасположенных проводников прямоугольной формы толщины T=0. Ширина зазора составляет 0,1 мм, диэлектрическая проницаемость материала . Размеры выбраны так, чтобы получить наглядную характеристику передачи. В общем случае размеры ограничиваются областью применимости используемой волноводной модели резонатора. Полученные результаты сравнивались c расчетами методами полного электромагнитного анализа: методом моментов (МоМ) и методом конечных элементов (МКЭ). Итоговые результаты представлены в виде матрицы рассеяния четырехполюсника с выводами шириной 1 мм по центрам противоположных друг другу краев резонаторов. Графики соответствуют 5625 КЭ и 300 выводам на каждом резонаторе. Количество элементов в данном примере взято с излишком, чтобы гарантировать низкую погрешность моделирования. Время расчета 100 частотных точек составило менее одной минуты. Применение более высокого порядка аппроксимации плотности заряда в методе моментов позволит существенно снизить количество элементов и время расчета. Видно хорошее совпадение расчетных характеристик в диапазоне частот до 10 ГГц при равномерном диэлектрическом заполнении, что согласуется с принятыми приближениями. Внешний вид топологий и соответствующие коэффициенты передачи S21 приведены на рис.4 и рис.5.

В процессе проведения численного эксперимента было установлено, что ширина кривой в области резонанса зависит от корректности распределения по выводам взаимных частичных емкостей, которые моделируют эффекты излучения и приема сигнала. На сдвиг по частоте влияет точность определения краевой емкости. Высота пика превышает пики в расчетах строгими методами. Это объясняется тем, что в решаемой задаче слой безграничного диэлектрика над проводником имеет такую же высокую диэлектрическую проницаемость, как и подложка, из-за чего распределение поля хуже соответствует приближению волноводной модели резонатора. Более интересные для практики конфигурации диэлектриков, такие как МПЛ или СПЛ, больше соответствуют физическим приближениям метода. Поэтому дальнейшее развитие программы планируется в направлении модификаций квазистатического расчета на основе многослойных планарных структур. Планируется также повысить точность существующей модели и сократить объем необходимых вычислений путем аппроксимации распределения зарядов базисными функциями более высокого порядка и оптимизации количества необходимых соединений.

4.      Заключение

Представленная реализация разработанного метода позволила рассчитать приближенные характеристики коэффициентов передачи связанных резонаторов в диапазоне частот от 1 до 10 ГГц за приемлемое время и может быть оптимизирована и обобщена на практически интересные случаи. Для эффективного применения на практике, программа требует детальной проработки алгоритмической реализации методов композиции сложных схем.

Литература

1. В.В.Радченко, Исследование методов повышения точности электростатического моделирования пассивных СВЧ устройств на основе планарных структур. // Сборник научных трудов ФГУП «ЦНИРТИ им. академика А.И.Берга».2011г.- ч .2, - с.76-98.

2. R. Mongia, I. Bahl, and P. Bhartia, RF and Microwave Coupled-Line Circuits // Artech House, Norwood, MA, 1999.

3. K. C. Gupta, Peter S. Hall - Analysis and Design of Integrated Circuit-Antenna Modules // by John Wiley & Sons, 2000.

4.  Гупта К., Гардж Р., Чадха Р., Машинное проектирование СВЧ устройств // М: Радио и связь, 1987.

5. Иосель Ю. Я., Кочанов Э. С., Струнский М. Г. Расчет электрической емкости // Энергоатомиздат, 1981.

6. T. Okoshi, T. Miyoshi: The Planar Circuit – An Approach to Microwave Integrated Circuitry // IEEE Trans. MTT-20, pp. 245–252, 1972.

7. Janusz A. Dobrowolski., Introduction to Computer. Methods for Microwave Circuit. Analysis and Design. // Warsaw University of Technology. Artech House, 1991.