| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 7 , 2000 |
СЛУЧАЙНЫЕ ПОТОКИ ИМПУЛЬСОВ С ЗАДАННЫМИ КОРРЕЛЯЦИОННЫМИ СВОЙСТВАМИ
Голик Ф.В.
Новгородский государственный университет им. Ярослава МудрогоПолучена 6 июля 2000 г.
Исследуются случайные потоки импульсов с независимыми длительностями импульсов и пауз и постоянной амплитудой. Сформулировано требование к автоковариационной функции потока (АКФ) – АКФ монотонно убывает на интервале заданной длины. Доказано существование потоков, удовлетворяющих этому требованию, и решена задача их синтеза. Определены характеристики потоков и проведена их классификация. Синтезированные потоки могут найти применение в асинхронных системах передачи информации с вероятностным разделением каналов, в радиолокационных системах с перестраиваемыми параметрами, а так же в других системах, эффективность функционирования которых повышается при уменьшении корреляционной связи между импульсными воздействиями.
Введение
Под случайными потоками импульсов будем понимать потоки, длительности импульсов t и пауз q которых случайны, а амплитуды импульсов постоянны и равны единице. Процессы такого типа широко используются в качестве моделей при исследовании систем передачи информации, радиолокационных систем, систем управления и др.
Исследованию потоков посвящены многочисленные работы отечественных и зарубежных авторов, усилиями которых решены вопросы анализа потоков. Вместе с тем в связи с широким внедрением асинхронных методов передачи информации, активным использованием методов оперативной перестройки параметров радиолокационных систем с целью обеспечения скрытности их работы, появилась необходимость решения задач синтеза потоков, обладающих заданными свойствами. Дело в том, что рассматриваемые потоки используются в этих системах в качестве управляющих. Так, в импульсных асинхронных системах с многократной передачей сообщений потоки управляют режимом информационного обмена. При этом вероятность искажения сигналов вследствие их временного наложения зависит от корреляционных свойств управляющего потока. При прочих равных условиях вероятность искажения минимальна, если автоковариационная (АКФ) функция потока быстро затухает и равна нулю при задержках, больших длительности сигнала [1].
Аналогичные требования предъявляются к потокам, используемым в качестве управляющих сигналов в радиолокационных системах с перестраиваемыми параметрами.
Проблема синтеза потока с "узкой" АКФ возникает при формировании стимулирующих электрических сигналов в медицине.
Настоящая работа посвящена решению задачи синтеза случайных потоков с независимыми длительностями импульсов и пауз и имеющих АКФ, не равные нулю на интервале заданной длины и монотонно убывающие в пределах этого интервала.
y ,a
-потокиИзвестно [2], что изображение Лапласа нормированной АКФ потока импульсов с независимыми длительностями импульсов и пауз равно:
где
,
,
![]() -математические ожидания длительностей
импульсов и пауз соответственно; a(s),
b(s) -
изображения плотностей распределения
длительностей импульсов a (x)
и пауз b
(x).
-математические ожидания длительностей
импульсов и пауз соответственно; a(s),
b(s) -
изображения плотностей распределения
длительностей импульсов a (x)
и пауз b
(x).
Приведем выражение (1) к следующему виду:
где d - постоянный коэффициент, а
y - некоторая функция a(s).Поток, изображение АКФ которого задано выражением (2), будем называть y
,a -потоком, а плотность распределения a (x) - порождающей.Потребуем выполнения следующих условий:
1) a (x
) - финитная функция, заданная на2) r (t
) - нормированная АКФ, отличная от 0 на3) r (t
) монотонно убывает на интервалеПоток, для которого выполняются условия 2), 3) обладает "хорошей" АКФ. Задача синтеза потока с заданными корреляционными свойствами будет решена, если удастся найти функцию
y .Доказана теорема, утверждающая, что условия
2) и 3) выполняются тогда и только тогда, когда выполняется условие 1) и функция y равна:Введем коэффициенты
Тогда АКФ потока, удовлетворяющего условиям 1), 2), 3), равна:
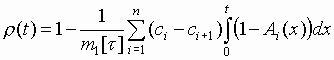 ,
,
где
 ,
,
Свойства и характеристики
y ,a -потоковЕсли упорядочить множители
![]() ,
,
то АКФ
y , a -потока монотонно убывает. Действительно, производная нормированной АКФ неположительна во всей области определения: .
.
Более того, из выражения для производной видно, что она остается неположительной независимо от выполнения условия 1) – финитности порождающей плотности распределения. Отсюда следует, что АКФ
y ,a -потока монотонно убывает наВажной характеристикой потока является время корреляции. Можно показать, что время корреляции y
,a -потока равно:где
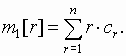
Поток случайных импульсов полностью задан, если известны плотности распределения длительностей импульсов и пауз. Плотность распределения импульсов a
(x) известна, а плотность длительности пауз b (x) можно найти по ее изображению b(s), которое достаточно просто определяется на основании соотношений (1), (2) и (3):Поскольку
 <1,
то выражение (6) представимо
бесконечной геометрической прогрессией.
При этом нахождение оригинала плотности
распределения b (x)
в большинстве случаев не вызывает
затруднения.
<1,
то выражение (6) представимо
бесконечной геометрической прогрессией.
При этом нахождение оригинала плотности
распределения b (x)
в большинстве случаев не вызывает
затруднения.
На основании выражения (6) можно найти числовые характеристики длительности пауз q
:математическое ожидание:
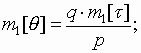
дисперсия
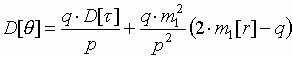 ,
,
где
D[t ] – дисперсия длительности импульсов потока.Коэффициенты
![]()
Этим требованиям удовлетворяют дискретное равномерное и геометрическое распределения. Для пуассоновского и биномиального законов необходимо наложить ограничения на параметры. Таким образом, можно синтезировать
y ,a -потоки с заданным распределением коэффициентовy ,a -поток:Равномерный
![]()
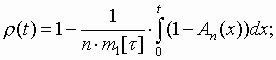
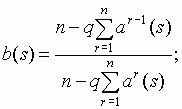
Геометрический
y ,a -поток:![]()
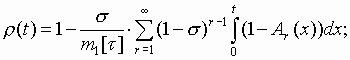

Пуассоновский
y ,a -поток:
y , a -потоки с минимальным временем корреляции
Из соотношения (5) следует, что
при прочих равных условиях время
корреляции ![]() принимает минимальное значение при n=1.
принимает минимальное значение при n=1.
Тогда
Из выражения (9) видно, что плотность распределения длительности пауз b
(x) равна смеси k-кратных сверток порождающей плотности a (x) с весами, равными вероятностям геометрического распределения. Это дает основание называть такой поток y ,a -геометрическим.Рассмотрим наиболее интересные с практической точки зрения частные случаи потоков при различных порождающих плотностях
a .1.При постоянной длительности импульсов (
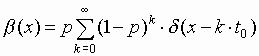 .
.
Время корреляции равно
2. Если импульсы потока состоят из случайного числа
k+1 блоков фиксированной длительности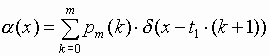 .
.
В частном случае при биномиальном распределении
 .
.
Здесь
Нормированная АКФ равна:
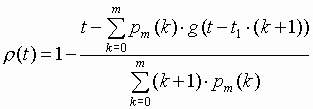 ,
,
где
 .
.
3. Пусть порождающая функция
a (x) - произвольная плотность распределения неотрицательной случайной величины. Зададим плотность распределения длительности импульсов выражением: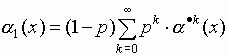 .
.
Из (8) следует, что
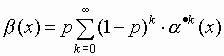 .
.
При этом АКФ в точности совпадает с АКФ a -геометрического потока (7). Потоки с такими "симметричными" распределениями длительностей импульсов и пауз будем называть двусторонними
a -геометрическими [4].Классификация
y ,a -потоковКак следует из
выражения (2) АКФ потока зависит от
функции y
, которая в свою очередь определяется
совокупностью множителей ![]() (или коэффициентов
(или коэффициентов ![]() из (3)) и их количеством n. Кроме
того, АКФ зависит от порождающей плотности
распределения
a
. Поэтому y
,a -потоки
можно классифицировать:
из (3)) и их количеством n. Кроме
того, АКФ зависит от порождающей плотности
распределения
a
. Поэтому y
,a -потоки
можно классифицировать:
При n>1 различают потоки с произвольной совокупностью множителей
При
n=1 различают односторонние и двусторонние a -геометрические потоки. Они имеют одинаковые АКФ, однако отличаются числовыми характеристиками длительностей импульсов и пауз.Порождающую плотность распределения a можно классифицировать по протяженности области определения. Если a определена на интервале конечной длины
Заключение
Итак, на основании приведенных соотношений можно синтезировать случайные потоки импульсов, АКФ которых удовлетворяют достаточно жестким требованиям. Выбор порождающих функций позволяет решать задачи синтеза применительно к конкретным прикладным проблемам.
Полученные результаты могут быть использованы при оптимизации процедуры стохастического временного разделения каналов в импульсных асинхронных системах передачи информации. В частности, реализация предложенных методов позволила существенно повысить эффективность систем вторичной радиолокации и бортовых
систем предотвращения столкновений самолетов в воздухе. Кроме того, синтезированные потоки могут с успехом применяться и в других технических системах, эффективность функционирования которых повышается при уменьшении корреляционной связи между импульсными воздействиями.ЛИТЕРАТУРА
1. Голик Ф.В. Многомерные импульсные потоки в теории асинхронных радиотехнических систем //Радиотехника. - 1991. - с. 18-19.
2. Седякин Н.М. Элементы теории случайных импульсных потоков. М.: Сов. радио, 1965.
3. Левин Б.Р. Теоретические основы статистической радиотехники. М.: Сов. радио, 1966. Кн.1.
4. Голик Ф.В. Потоки прямоугольных импульсов с "хорошей" автоковариационной функцией //Радиотехника и электроника. - 1991. - т. 36, № 11, с. 2141-2147.
Автор:
Голик Феликс Валентинович, профессор кафедры "Радиосистемы" Новгородского государственного университета им. Ярослава Мудрого, e-mail: gfv@info.novsu.ac.ru