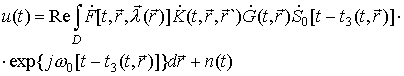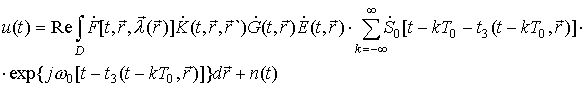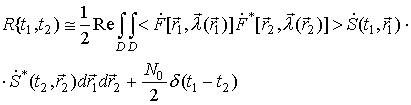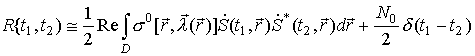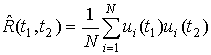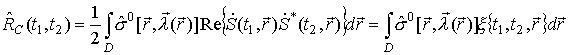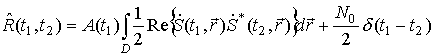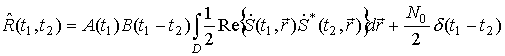"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 6, 2001

оглавление

дискуссия

СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОТРАЖЕННЫХ СИГНАЛОВ ДЛЯ СТОХАСТИЧЕСКИХ МОДЕЛЕЙ ПОВЕРХНОСТИ И ИХ ОЦЕНКА

А. В. Ксендзук

Харьковский Национальный Аэрокосмический Университет им Н. Е. Жуковского

 

Получена 30 мая 2001 г.

 

В статье рассмотрены основные свойства отраженных сигналов для стохастических моделей рассеянного электромагнитного поля. Для систем РСА получено аналитическое выражение для статистических характеристик принимаемого антенной сигнала в случае непреравного и импульсного излучаемого сигналов. Рассмотрены различные методы оценки корреляционных функций принимаемого сигнала и получены характеристики таких оценок (смещения относительного истинного значения и дисперсии). Показано поведение рассмотренных оценок на основании данных спутниковой системы РСА SIR/X-SAR.

 1  Модель отраженного сигнала

При отражении радиолокационный сигнал претерпевает ряд изменений, связанных со свойствами отражающих (рассеивающих) объектов. При этом, например, для задач картографирования естественно различать полезный сигнал, полученный в результате отражения от зондируемой поверхности и мешающие сигналы, обусловленные отражениями от маскирующих объектов (облака и другие гидрометеоры, турбулентности атмосферы), собственными шумами приемника, атмосферным шумом, активными помехами и др.

Общие соотношения для принимаемого сигнала можно установить через зависимость мощности отраженного сигнала от дальности до цели и ее эффективной отражающей поверхности, частоты и задержки - от скорости взаимного движения цели относительно носителя и дальности, соответственно.

Более точные соотношения находятся в результате решения прямых дифракционных задач при заданных граничных условиях. Однако в большинстве случаев решение таких задач возможно только для достаточно узкого класса моделей поверхности. Наиболее часто используемыми являются модели мелкомасштабной и крупномасштабной поверхности, фацетная модель  и также другие комбинированные модели, [1], [2].

Зависимость мощности и амплитуды отраженного сигнала от ракурса облучаемого участка поверхности представляется обычно  в виде диаграммы вторичного излучения. Для объектов простой геометрической формы диаграмма вторичного излучения может быть рассчитана теоретически в результате решения электродинамических задач. Но для реальных сложно конфигурированных элементов провести такой расчет обычно не удается. Более того, в реальных условия функционирования РЛС такие диаграммы являются лишь статистическими характеристиками, так как за счет взаимного движения элементов картографируемой поверхности и РЛС,  изменения условий распространения радиоволн отраженный сигнал всегда флуктуирует.  При этом причинами флуктуаций могут также выступать вибрация (изменение) поверхности объектов, случайные изменения диаграмм направленности антенн, положения зондирующей РЛС и др.

В силу вышеперечисленных причин отраженный от поверхности сигнал можно представить случайным процессом, [3], поэтому возможно перейти к  стохастическим моделям отраженного (рассеянного) электромагнитного поля. Данные модели,  в отличие от функционально - детерминированных,  содержат флуктуации амплитуды и фазы отраженного от поверхности поля. Рассмотрим основные статистические характеристики для таких моделей.

Уравнение наблюдения запишем в виде:

 ,                                                                            (1)

где- сигнал, отраженный от зондируемой поверхности ;  - комплексная функция, характеризующая отражающие свойства элемента поверхности с координатами  и электрофизическими параметрами  (диэлектрическая проницаемость, проводимость, влажность и др.);- сигнал, который был бы принят от элемента поверхности с координатами  при условии ;  - аддитивный шум, который далее будем полагать нормальным с равномерной  спектральной плотностью  и нулевым средним.

По своему физическому смыслу  соответствует отношению коэффициента рассеяния (отражения) элемента поверхности  к площади этого участка и находится в результате решения прямых дифракционных задач при регулярных или случайных граничных условиях. При использовании стохастических моделей отраженного электромагнитного поля  представляет собой случайный процесс, обычно нестационарный в пространстве. Так как для принятых к рассмотрению моделей поверхности отражающая способность является случайной величиной, то впоследствии  будем называть стохастическим изображением поверхности, а  - статистически  усредненным изображением.

Адекватное описание процесса   достаточно сложно, наиболее полной его характеристикой является совокупность многомерных распределений вероятности значений , [3]. Однако найти такую статистическую характеристику для широкого класса поверхностей достаточно трудно. В связи с этим обычно используются некоторые упрощенные модели поверхности. В качестве такой модели удобно использовать представление зондируемой поверхности в виде большой совокупности независимо и случайно расположенных отражающих элементов (элементарных отражателей), которые могут быть неподвижными либо перемещаться в пространстве. Физическим обоснованием такой модели является принцип Гюйгенса- Кирхгофа, по которому каждая точка пространства, в которую приходит электромагнитная волна, может рассматриваться как источник вторичной сферической волны, [4]. Причем такая модель охватывает не только  поверхности со случайными изменениями рельефа, но и поверхности с изменяющимися электрофизическими параметрами. Об эквивалентности (в смысле формирования отраженного сигнала) изменяющихся электрофизических характеристик поверхности и шероховатости ее поверхности упоминается, в частности, в работе [5].

Запишем сигнал, подводимый к антенне (сигнал передатчика):

,                                           

где  - комплексная огибающая, ;  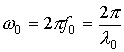 -параметры несущей (частота, длина волны) излучаемого сигнала.

Излучаемый антенной сигнал в направлении i-й точки поверхности (элементарного рассеивателя/отражателя):

,

где   - комплексная переменная, учитывающая диаграмму  направленности антенны на передачу (или диаграмму направленности передающей антенны, если для приема и передачи используются различные антенны) для i-й точки, в общем случае зависит от времени по причине, например, движения и/или вращения антенны.

Отраженный от i-й точки поверхности сигнал определяется выражением:

,

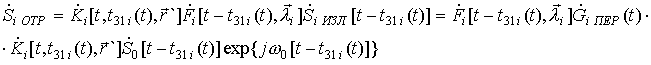где     - комплексная огибающая излучаемого сигнала, задержанная на  - время запаздывания, связанное с прохождением сигнала от антенны (в случае разнесенных в пространстве антенн – от передающей антенны) к i-й отражающей точке; - комплексный коэффициент отражения сигнал от i-й точки поверхности, в общем случае зависит от времени и  электрофизических параметров поверхности (диэлектрическая проницаемость, проводимость, влажность и другие);  - коэффициент, учитывающий искажения сигнала при распространении его через атмосферу от передающей антенны к точке поверхности, - координаты раскрыва антенны.

Принимаемый антенной сигнал после отражения его от i-го элемента поверхности:

 

,

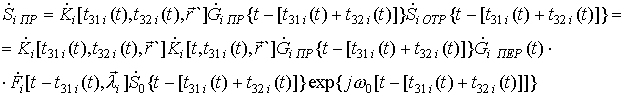где - время запаздывания, связанное с прохождением сигнала от отражающей точки к антенне (к приемной антенне);  - комплексная переменная, учитывающая диаграмму  направленности приемной антенны для i-й точки поверхности; - коэффициент, учитывающий искажения сигнала при  распространении через атмосферу от отражающей точке к приемной антенне.

Вышеприведенное выражение описывает общий случай дистанционного зондирования. Однако обычно более удобно воспользоваться упрощенным выражением.  Рассмотрим случай моностатической радиолокации – передающая и приемная антенна совмещены. При этом будем полагать, что коэффициенты, описывающие диаграммы направленности антенны  и искажения при распространении сигнала через атмосферу  не изменяются за время задержки импульса. Также будем считать, что коэффициент отражения не является функцией времени , время задержки аппроксимируем его средним значением , где  - изменение расстояния между антенной и элементарным отражателем.

С учетом этих упрощений, сигнал, отраженный от элемента поверхности с координатами , запишем таким образом:

 

,                                        (2)

 

где  - коэффициент, отражающий влияние диаграмм направленности антенны;  - описывает изменение (искажение) сигнала при распространении его через атмосферу; - комплексная огибающая излучаемого сигнала; - закон изменения фазы излучаемого сигнала;  - полное время задержки на распространение сигнала (от момента его излучения антенной до момента приема отраженного от точки с координатами  ).

Если излучаемый сигнал представляет собой последовательность импульсов, выражение (2) можно записать следующим образом:

,                                       (3)

где  - комплексная огибающая пачки импульсов; - комплексная огибающая одиночного импульса; - период повторения зондирующих импульсов.

В выражении (3) суммирование по  взято в бесконечных пределах, так как существует срезающая во времени функция , которая вырезает некоторую конечную последовательность импульсов.

Тогда принимаемый антенной сигнал в рамках принятой упрощенной модели будет представлять собой сумму сигналов , отраженных от отдельных элементов в пределах следа диаграммы направленности на поверхности , и шума : . В силу центральной предельной теоремы процесс на входе антенны можно считать распределенным по нормальному закону; экспериментальные исследования, [3], показывают, что в большинстве случаев предположение о нормальном характере отраженного поля верно.

Переход от совокупности элементарных отражателей к сплошной поверхности можно осуществить при предельном переходе к бесконечно малым элементарным отражателям  следующим образом: , где  - след антенны на поверхности;  -  координаты пространства;  - принимаемый сигнал от элементарного отражателя . Такой переход не вполне корректен, однако может использоваться, если в пределах элемента разрешения содержится множество независимых отражателей. Окончательно, модель принимаемого антенной сигнала зададим, используя (1) и (2), следующим образом:

 

,                                                     (4)

Для импульсного излучаемого сигнала принимаемый антенной сигнал можно записать при учете (1), (3) следующим образом:

.         (5)

В дальнейшем будем полагать принимаемый антенной сигнал  распределенным по нормальному  закону. Как известно, для полного описания такого класса случайных процессов  достаточно знание первых двух статистических моментов – математического ожидания и корреляционной функции.

 

2 Статистические характеристики отраженного поля

Рассмотрим статистические характеристики принимаемого сигнала для стохастических моделей поверхности. Обычно среднее значение отраженного от поверхности сигнала равно нулю, [4]. Это означает что , ранее оговаривалось, что среднее аддитивного шума полагается равным нулю. Таким образом, для того чтобы полностью описать принимаемый сигнал достаточно найти его корреляционную функцию, определяемую выражением  . Подставив сюда уравнение наблюдения (1) , получим:

.  

Поле несложных преобразований, при условии что случайные процессы  и  статистически независимы, причем , получим:

.                  

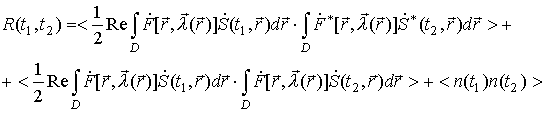Считая, что членами, содержащие удвоенную несущую частоту, можно пренебречь (в силу леммы Римана для конечного промежутка, [6]), получим следующее выражение для корреляционной функции:

,                                                    (6)

Это же выражение для импульсного излучаемого сигнала можно записать следующим образом:

 

(7)

В рамках принятой упрощенной модели поверхности можно считать процесс  дельта-коррелированным в пространстве , то есть:

 

                                                          (8)

где - величина, равная удельной эффективной поверхности рассеяния (УЭПР) элемента поверхности; - дельта-функция.

Как упоминалось ранее, данное представление не вполне корректно, однако может использоваться, если в пределах элемента разрешения содержится большое число элементарных отражателей. Тогда (6) при  учете (8) примет вид:

.                                                (9)

Для импульсного излучаемого сигнала это же выражение может быть записано следующим образом:

 

.(10)

Из выражений (9), (10) нетрудно увидеть, что максимальная длительность корреляционной функции ограничивается двойным потенциальным интервалом синтезирования . В случае бокового обзора и равномерного прямолинейного движения вдоль одной из осей  это время определяется соотношением , где - след диаграммы направленности антенны на поверхности по оси  движение ЛА,   - скорость движения носителя по этой оси.

Так как интегрирование по пространству осуществляется в области, определяющейся произведением следов диаграмм направленности антенны на поверхности, очевидно, что корреляционная функция в общем случае будет убывать при увеличении разности между отсчетами времени  и . Также необходимо отметить, что в общем случае корреляционная функция является несимметричной по причине несимметричности ЭПР в зоне обзора.

При импульсном режиме работы эта функция будет иметь периодический характер с периодом повторения равным периоду следования зондирующих импульсов .

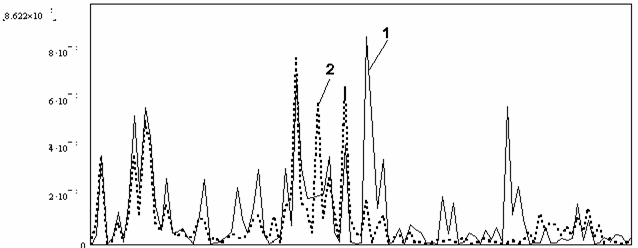
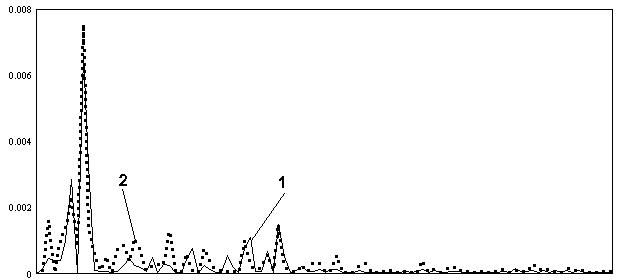
Пример поведения корреляционной функции (10) для импульсного режима работы РСА и укрупненный вид одного из периодов приведены ниже на рис.1 (в качестве изображения поверхности использовались данные путника SIR/X SAR, [7]).

 

Рис.1. Общий вид сечения корреляционной функции принимаемого сигнала.

 

На рисунке 1 приняты следующие обозначения: -сечение корреляционной функции при фиксированном значении ; -потенциальное время синтеза; - период повторения зондирующих импульсов; - длительность импульса.

 

3 Оценка статистических характеристик принимаемого сигнала

 

Оценка корреляционной функции по ансамблю реализаций

Если имеется набор из  независимых реализаций входного сигнала, полученных, например, с помощью многолучевой РСА, то оценку корреляционной функции   можно произвести путем усреднения по ансамблю реализаций:

.                                                                                                      (11)

При этом характеристики такой оценки определяется выражениями:

,                                            

.                

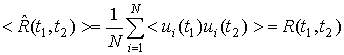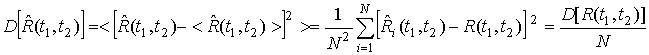С помощью среднего значения и среднеквадратического отклонения можно для любых  оценить вероятность отклонений оценки, не зная ее точной функции распределения  . Для этого используется  неравенство  Чебышева:

 

,

где - некоторая константа; - вероятность события .

Здесь знак равенства определяет граничные значения, между которыми с  вероятностью не меньшей  лежит среднее значение оценки :

.

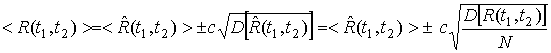Из этого выражения следует, в частности, что, независимо от величины дисперсии корреляционной функции  и закона распределения, при   оценка всегда будет состоятельной при конечном математическом ожидании выборки независимо от величины дисперсии.

При коррелированных реализациях в ансамбле (функция  корреляции ), по которому производится оценка, дисперсии полученной оценки корреляционной функции будет определяться следующим образом:

.

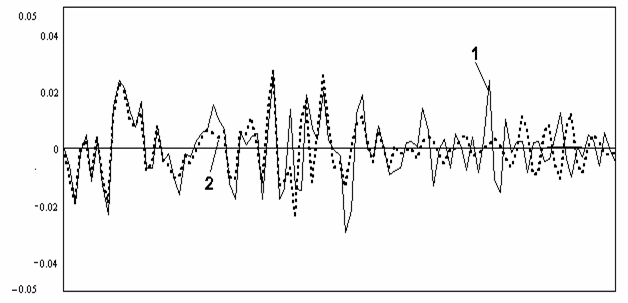
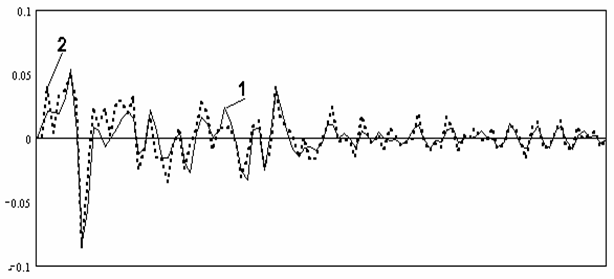
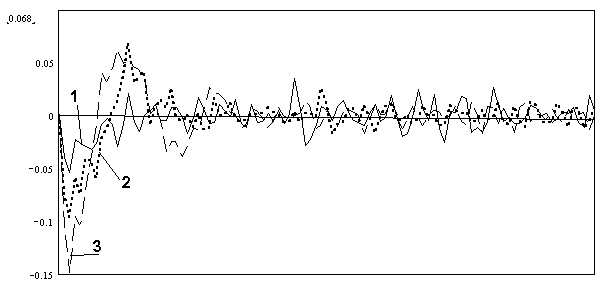
На рисунках 2, 3 приведен пример поведения  смещения и дисперсии оценок корреляционной функции принимаемого сигнала при таком методе получения статистических характеристик. При этом в качестве исходных данных использовались параметры спутниковой РСА SIR/X-SAR, [7].

 

Рис.2. Смещение оценки корреляционной функции. 1- усреднение по 10 реализациям; 2- по 20 реализациям; 3- по 50 реализациям.

 

Рис.3. Дисперсия оценки корреляционной функции. 1- усреднение по 10 реализациям; 2- по 20 реализациям; 3- по 50 реализациям.

 

Как видно из рисунков 2, 3 при усреднении по большему ансамблю реализаций входного сигнала происходит уменьшение смещения и дисперсии оценки корреляционной функции принимаемого сигнала.

 

Оценка корреляционной функции по одной реализации.

Часто приходится иметь дело с одной реализацией случайного процесса (например, в однолучевой РСА), что делает невозможным нахождение статистических характеристик принимаемого сигнала путем усреднения по ансамблю. В такой ситуации для оценки корреляционной функции принимаемого сигнала можно воспользоваться определением статистических характеристик поверхности (УЭПР). Обычно величину  полагают известной и находят в процессе калибровки РЛС, поэтому для оценки корреляционной функции принимаемого сигнала  достаточно найти удельную эффективную поверхность рассеяния  в пределах области обзора. После этого оценку корреляционной функции можно произвести путем подстановки соответствующих параметров РСА в выражения (9), (10).

При таком методе оценочное значение сигнальной части корреляционной функции принимаемого сигнала записывается следующим образом:

 

, (12)

где  - полученная оценка УЭПР.

Найдем характеристики такой оценки:

 

,

.

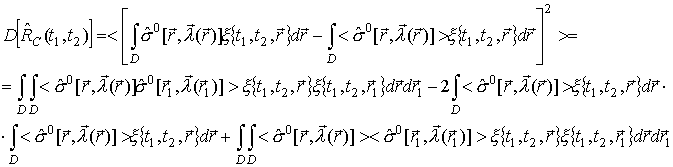Последнее выражение может быть записано следующим образом:

 

,

где  пространственные корреляционные функции оценки УЭПР и среднего оценки УЭПР.

Для дальнейших рассуждений ниже приведено поведение пространственно-временной гармоники  в пределах области обзора на примере системы SIR/X-SAR. Рассмотрим ее пространственные частоты; аналитические выражения для них получены в декартовых координатах  для равномерного движения РСА вдоль одной из осей (ОХ):

 

,     

,

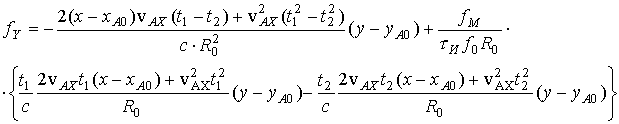где  - начальное положение фазового центра антенны; - скорость движения носителя;  - координаты точки поверхности.

Графическое представление поведения функции   в области обзора показано ниже.

 

 

 

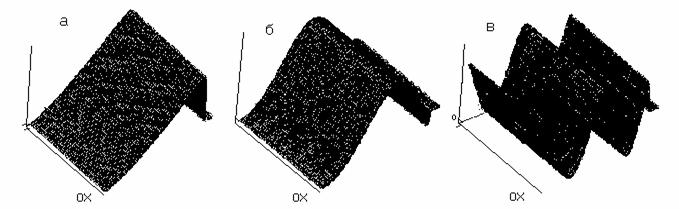
Рис.4. Поведение пространственно-временной гармоники.

 

  На рисунках 4 а-в изображено поведение пространственно-временной гармоники в пределах области обзора, разность  невелика (значения равны  0.01, 0.1, 0.2 длительности импульса, соответственно). При некотором значении разности  частота пространственно-временной гармоники становится такой, что в пространственном интервале разрешения РСА находится несколько периодов пространственной гармоники. Пример такого поведения функции  показан на рисунке 5.

 

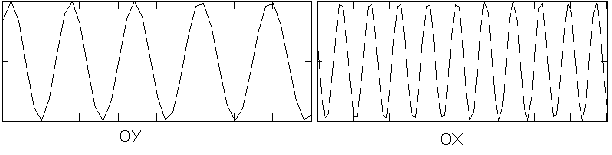
Рис.5.  Поведение пространственно-временной гармоники, размер рисунков соответствует разрешающей способности РСА.

 

Исходя из поведения функции  можно сделать несколько выводов:

при таком способе оценки корреляционной функции принимаемого сигнала неизбежно будет возникать ошибка, связанная с тем, что пространственная частота гармоники  выше обеспечиваемого системой разрешения;

ошибки оценки УЭПР наиболее влияют на вид корреляционной функции при малых разностях ;

при таком оценивании наиболее значительный вклад вносят погрешности оценки низкочастотных компонент  .

 

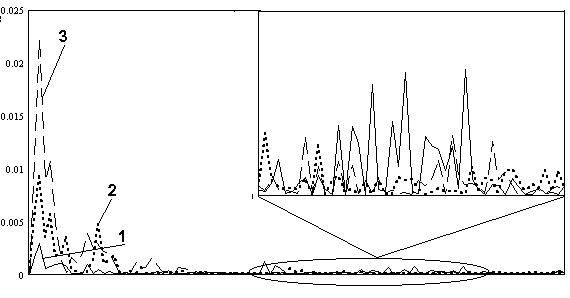
Ниже на рисунках 6, 7 приведены характеристики оценки корреляционной функции, выполняемые в соответствии с (12). При моделировании использовались данные системы SIR/X-SAR, для большей наглядности применялся континуальный аналог корреляционной функции принимаемого сигнала.

 

 

Рис.6. Смещение оценки корреляционной функции (19). 1- при узкой искажающей функции (пространственно функции неопределенности); 2- при широкой.

 

 

 

Рис.7. Дисперсия  оценки (19). Здесь 1- при узкой искажающей функции; 2- при широкой искажающей  функции.

 

Соотношение (12) можно представить как выражение для коэффициентов ряда разложения  по функциям . В таком контексте можно приближенно оценить корреляционную функцию   путем усечения ряда до нескольких членов. Этот факт позволяет приближенно оценивать статистические характеристики сигнала в реальном масштабе времени.

Пусть в некоторый момент времени  фазовый центр антенны находится в точке 1, тогда корреляционная функция  будет отлична от нуля на интервале , как показано ниже на рис.8. Для некоторого момента времени можно получить приближенное выражение для  в соответствии с (12) путем использования в качестве функции  среднего значения в пределах области обзора. Это значение можно получить, например, путем вычисления мгновенной мощности отраженного от поверхности сигнала.

 

Рис.8. Геометрия РСА.

 

Тогда выражение ля корреляционной функции может быть записано так:

,                                              (13)

где - среднее значение ЭПР в момент .

Характеристики такой оценки определяются следующими  выражениями:

 

,

,

где - корреляционная функция ЭПР поверхности.

Другим вариантом при этом может являться использование некоторых функций, зависящих от разности :

,                             (14)

где - среднее значение ЭПР в момент , - некоторая выбранная функция.

Смещение и дисперсия такой оценки определяются следующими выражениями:

 

,

,

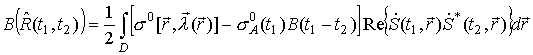где - корреляционная функция ЭПР поверхности относительно выбранной модели.

Ниже на рисунках 9, 10 приведены характеристики оценки корреляционной функции, выполняемые в соответствии с (13), (14). При моделировании использовались данные системы SIR/X-SAR, для большей наглядности применялся континуальный аналог корреляционной функции принимаемого сигнала.

 

Рис.9. Смещение оценки корреляционной функции при оценке в реальном масштабе времени. 1- при использовании (13); 2- при использовании (14), - экспоненциальная функция.

 

 

 

Рис.10. Дисперсия оценки корреляционной функции при оценке в реальном масштабе времени. 1- при использовании (13); 2- при использовании (14), - экспоненциальная функция.

 

 

Одним из вариантов оценки в реальном режиме времени является усреднение полученных значений оценок корреляционной функции на нескольких периодах повторения зондирующих импульсов. Такая оценка может быть получена следующим образом:

                                                                             (15)

Это выражение может использоваться, если расстояние, проходимое носителем за время повторения импульса невелико, а зондируемую поверхность в пределах этого расстояния не содержит элементов, существенно влияющих на  общие характеристики отраженного сигнала. Погрешность усреднения по различным периодам может быть записана  следующим образом: 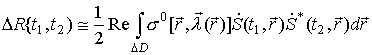, где - интервал "несовпадения" диаграмм направленности в пространстве. Геометрические характеристики данного метода показаны на рис. 11.                                                           

 

Рис.11. Ошибка при усреднении по соседним периодам.

 

При использовании этого метода необходимо учесть, что усреднение происходит по небольшому числу условно независимых реализаций, поэтому результат такой оценки не является "достаточно хорошим". При этом характеристики такой оценки будут следующими:

,                                                

.

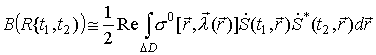На рисунках 12, 13 приведены характеристики оценки корреляционной функции, выполняемые в соответствии с (15). При моделировании использовались данные системы SIR/X-SAR, для большей наглядности применялся континуальный аналог корреляционной функции принимаемого сигнала.

 

 

Рис.12. Смещение оценки (15). 1- при усреднении в пределах 3-х периодов повторения импульсов; 2- в пределах 9; 3- в пределах 15 периодов.

 

 

Рис.13. Дисперсия оценки (15). Здесь 1- при усреднении в пределах 3-х периодов  повторения импульсов; 2- в пределах 9; 3- в пределах 15 периодов

 

 

На основании приведенных выше соотношений и графиков для различных методов оценки корреляционной функции можно сделать следующие выводы:

·        Усреднение по ансамблю реализаций дает достаточно хорошие результаты при большом наборе независимых реализаций. Однако получение такого ансамбля достаточно сложно технически.

·        При оценке статистических характеристик поверхности с последующим использованием их для оценки корреляционной функции ошибки зависят от разрешающей способности системы. При плохой разрешающей способности наибольшие ошибки наблюдаются при больших разностях  (область высоких пространственных частот), что можно объяснять наличием спекл-шума высокой пространственной частоты. При высокой разрешающей способности большие ошибки возникают в области "средних пространственных частот", что объясняется тем, что пространственная частота полученных оценок мала. В области высоких частот не наблюдается значительных всплесков, так как производится сглаживание в большем пространственном интервале.

·      При оценке в реальном режиме времени ошибки оценки корреляционной функции достаточно велики по сравнению с предыдущими методами. При этом использование некоторых фиксированных функций  не дает значительного выигрыша по сравнению с использованием соотношения (14).

·      При усреднении по нескольким соседним периодам ошибки оценивания зависят от характеристик поверхности. В общем случае наиболее велики искажения при малой разности , величина искажений определяется характеристиками поверхности, скоростью перемещения носителя и периодом повторения импульсов. Усреднение в небольшом числе соседних периодов начиная с некоторой разности во времени дает меньшую ошибку, чем при оценке в соответствии с выражениями (13), (14).

 

Литература

 

1.      Радиолокационные методы исследования земли под ред. Ю.А. Мельника, -

Москва: 1980

2.      Волосюк В.К. Статистические методы оценивания параметров электродинамических моделей земной поверхности при дистанционном зондировании- Харьков: ХАИ 1991

3.      Бакут П.А. Вопросы статистической теории радиолокации, том 1, - Москва: Советское радио, 1963

4.      Зубкович Статистические характеристики радиосигналов, отраженных от земной поверхности - Москва: Советское радио 1968

5.      Фейнберг Е.Л. Распространение радиоволн вдоль земной поверхности - Изд АН СССР, 1961

6.      Левин, Теоретические основы статистической радиотехники.

7.      СD SIR/X-SAR, Deutsche Agentur fur Raumfahrtangelegenheiten (DARA) GmbH