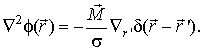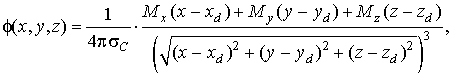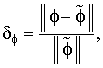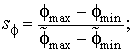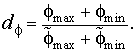Неоднородная электродинамическая модель грудной клетки человека в форме эллиптического цилиндра
Н. О. Стрелков, М. Н. Крамм, Г. В. Жихарева
Московский энергетический институт (Технический Университет)
Получена 12 июля 2011 г.
Аннотация. Целью данной работы является сравнение различных моделей грудной клетки (ГК), которые позволяют исследовать распределения электрического потенциала, возбуждаемого токовым источником в проводящей среде внутри ГК в квазистатическом приближении. Необходимость этого сравнения связана с задачей построения такой модели, которая, с одной стороны, была бы достаточно простой для интерпретации сигналов ЭКГ и для расчетов потенциала в прямых задачах электрокардиографии, и, с другой стороны, не вносила бы заметных искажений в карту потенциала на поверхности ГК. В работе рассматриваются модели ГК, в которых поверхность ГК имеет вид эллиптического цилиндра, а внутренняя проводящая среда содержит различные неоднородности, учитывающие проводимость и конфигурацию различных органов – сердца, заполненного кровью, легких, скелетных мышц, костей скелета и т.п. Проводится сравнение карт поверхностного потенциала (КПП), возбуждаемого дипольным токовым источником, по форме – с помощью коэффициента корреляции и нормированной погрешности, и по уровням потенциалов. Показано, что, полная неоднородная модель, включающая различные неоднородности, имеет карту поверхностных потенциалов, близкую по форме к карте для однородной грудной клетки, с коэффициентом корреляции, превышающим уровень 0.99.
Ключевые слова: грудная клетка, электрокардиография, прямая задача ЭКГ, карта поверхностного электрического потенциала, неоднородность, проводимость среды, картины линий токов.
Abstract. The aim of this study was to compare several torso models, which helps to analyze electric potential distributions caused by current source in conductive medium inside torso with quasi-static approximation. The necessity of such comparison comes from construction a model, which in on the one hand will be simple for electrocardiographic (ECG) signal interpretation and on the other hand will not add sufficient distortion to body surface potential map (BSPM). In this paper we presented different torso models, in which torso was constructed from elliptic cylinder with several inhomogeneities (represent heart with blood, lungs, skeletal muscle, skeletal bones, etc.). We did a comparison of BSPMs calculated from dipolar current source with help of correlation coefficient, normalized relative error, and potential levels. The results show that full inhomogeneous model (contains all inhomogeneities) has a BSPM which is similar to homogeneous torso model with correlation coefficient over 0.99.
Keywords: torso, electrocardiography, ECG forward problem, body surface potential map, inhomogeneity, medium conductivity, current streamline figure.
Введение
Основной методикой электрофизиологической диагностики состояния сердца является электрокардиография (ЭКГ). В ЭКГ широкое распространение получила дипольная концепция, согласно которой при определенных допущениях электрическую деятельность сердца можно описывать с помощью единого токового диполя, создающего в окружающем его объемном проводнике (теле человека) электрическое поле, которое может быть зарегистрировано с помощью электродов, расположенных на поверхности тела. Вектор единого сердечного диполя (ЕСД) представляет собой суммарный моментный вектор всех элементарных источников тока, существующих в данной фазе кардиоцикла [1].
Распределение электрического потенциала на поверхности грудной клетки (ГК) зависит не только от ориентации и координат ЕСД, но и от формы поверхности ГК и параметров внутренних неоднородностей – легких, костей скелета, мышечной ткани и т.п. [1]. В то же время в кардиологической практике для объяснения формы зубцов ЭКГ-сигналов в различных отведениях широко пользуются представлением об ЕСД в безграничной однородной проводящей среде [1-4]. В этой связи возникает вопрос о степени влияния неоднородностей ГК на распределение поверхностных потенциалов (ПП) и о правомочности использования модели безграничной однородной среды.
Следует также отметить, что в классической методике ЭКГ отсутствует количественное соотнесение поверхностных электрических потенциалов с характеристиками токовых источников сердца. Представляет интерес обратная задача электрокардиографии в терминах эквивалентных токовых источников: численная реконструкция параметров ЕСД (координаты и вектор токового момента) по измеренным электрическим потенциалам в точках расположения электродов [5]. Решение обратной задачи теми или иными итерационными процедурами предполагает использование алгоритма решения прямой задачи – расчета потенциалов на поверхности грудной клетки. При этом важным моментом является выбор адекватной электродинамической модели грудной клетки (ГК), которая должна учитывать форму поверхности ГК, а также параметры внутренней среды. Достоинством моделей простой формы является возможность представления поверхностного потенциала (ПП) в удобном для расчетов виде – с использованием аналитических формул и разложений в ряды. Таким образом, снова возникает вопрос о погрешностях, вносимых моделью ГК, и о влиянии учета неоднородностей внутренней среды.
Целью настоящей работы является анализ влияния неоднородностей внутренней среды и учета границы между ГК и воздухом на карты распределения поверхностного потенциала (КПП) и диапазон изменения ПП. В статье [6] проводится численно анализ влияния неоднородностей ГК на КПП, причем расчет основывается на конкретной записи потенциалов, снятых с поверхности эпикарда. Однако представляет интерес провести анализ при различном направлении перемещения волны возбуждения миокарда, отображаемой во многих моделях ориентацией единого сердечного диполя.
Модель ГК. Известны следующие модели: однородный шаровой проводник [1, 7]; кусочно-однородная модель в виде концентрических сфер [1]; кусочно-однородная модель в виде эксцентрических сфер [8]; модель в форме вытянутого [9] или сжатого проводящего сфероидов [10]; модель в форме кругового цилиндра [11-14]; модель в форме эллиптического цилиндра [13, 14]. В представленных моделях окружающей средой является воздух, причем две последние модели в большей степени приближены к анатомическим особенностями тела человека.
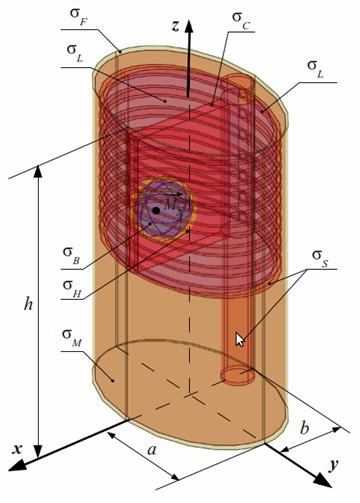
В настоящей работе предложена неоднородная модель ГК человека в форме эллиптического цилиндра, содержащего миокард и полость с кровью, кости (ребра, грудину и позвоночный столб), легкие, скелетные мышцы и слой подкожного жира (рис. 1). При расчете распределений электрического потенциала в качестве эквивалентного генератора сердца выступает токовый диполь, расположенный в центре сердца. Данная модель не ставит своей целью полностью повторить внутреннее строение тела человека, но, несмотря на это, нужна для выявления основных закономерностей в получаемых распределениях потенциалов при учете тех или иных неоднородностей.
В качестве примера размеры большой и малой полуосей
эллиптического цилиндра ГК взяты соответственно a = 18 см и b = 12 см, высота цилиндра h = 50 см (рис. 1).
Цилиндр окружен непроводящей средой – воздухом. Геометрические размеры
элементов модели подобраны в приближении к реальной анатомии человека [15]. Сердце представлено двумя
концентрическими сферами (соответствуют полости с
кровью и миокарду) радиусами 4.25 и 5 см с центром в точке (5, 0, 33.33) см. Данная модель содержит 7 ребер, называемыми в
анатомии “истинными”. Каждое ребро характеризуется
длинами большой и малой полуосей эллипсов – соответственно для внутренней и
внешней поверхностей – 15.9 и 10.6, 16.7 и 11.1 см. Высота отдельного
ребра принята равной 1.5 см, расстояние между ребрами составляет 2 см. Точка
пересечения осей эллипсов нижнего основания 7-го ребра
имеет координаты (0, 0, 25) см. Позвоночный столб представлен круговым
цилиндром радиуса 2.5 см и высоты 50 см,
центр нижнего основания которого расположен в точке (-8.8, 0, 0) см. Грудина
имеет вид эллиптического цилиндра с длинами полуосей 1.25 и 0.5 см, высотой 22.5 см, центр
нижнего основания находится в точке (10.8, 0, 25) см. Полость
грудной клетки представлена параллелепипедом с длиной, шириной и высотой
соответственно 22, 2 и 22.5 см, точка пересечения диагоналей нижнего
основания которого имеет координаты (-0.11, -0.01, 0.25) см.
Пространство легких формируется указанным параллелепипедом
и эллиптическим цилиндром с полуосями 15.1 и 10.1 см, высотой 22.5 см
и центром нижнего основания в точке (0, 0, 25) см. Слой кожи и подкожного жира
заключен между эллиптическими цилиндрами ГК и цилиндром с длинами полуосей 17.6
и 11.8 см и высотой 49 см с центром нижнего основания в точке (0, 0,
0.5) см. Скелетные мышцы ограничены с
одной стороны цилиндром кожи и подкожного жира, а с другой стороны – легкими. В соответствии с [6, 8] значения проводимостей выбраны следующими:
полость сердца с кровью – ![]() См/м, миокард –
См/м, миокард – ![]() См/м,
кости –
См/м,
кости – ![]() См/м, легкие –
См/м, легкие – ![]() См/м,
полость грудной клетки –
См/м,
полость грудной клетки – ![]() См/м, скелетные мышцы –
См/м, скелетные мышцы – ![]() См/м, кожа и подкожный жир –
См/м, кожа и подкожный жир – ![]() См/м. Оси декартовой системы координат показаны на рис. 1.
См/м. Оси декартовой системы координат показаны на рис. 1.
|
|
|
|
а) |
б) |
|
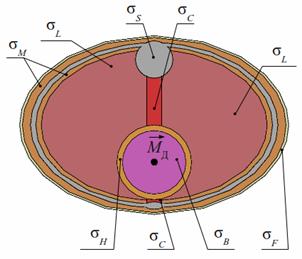
Рис. 1. Неоднородная модель грудной клетки человека в форме эллиптического цилиндра а) в объеме; б) сечение при z = 2h/3 (экватор сферы сердца) |
|
Расчет распределений потенциалов. Электрический потенциал в каждой точке пространства
однородной области внутри ГК с проводимостью ![]() подчиняется
уравнению Пуассона:
подчиняется
уравнению Пуассона:
|
|
(1) |
где радиус-вектор ![]() соответствует точке
наблюдения,
соответствует точке
наблюдения, ![]() - объемная плотность стороннего тока. Для
точечного дипольного источника
- объемная плотность стороннего тока. Для
точечного дипольного источника ![]() имеет вид
имеет вид
|
|
(2) |
где ![]() определяет момент токового
диполя, а
определяет момент токового
диполя, а ![]() - его расположение. Подставив (2) в
(1), получим:
- его расположение. Подставив (2) в
(1), получим:
|
|
(3) |
Потенциал ![]() на
границе ГК должен удовлетворять граничному условию Неймана
на
границе ГК должен удовлетворять граничному условию Неймана
|
|
(4) |
где ![]() – нормаль к поверхности
цилиндра.
– нормаль к поверхности
цилиндра.
При наличии внутренних неоднородностей для каждой пары с
известными проводимостями ![]() и
и ![]() справедливы граничные
условия:
справедливы граничные
условия:
|
|
(5) |
В настоящей работе распределения потенциалов на боковой поверхности эллиптического цилиндра, содержащего неоднородности (рис. 1), рассчитаны численно, методом конечных элементов.
Для определения влияния внутренних неоднородностей и внешней границы ГК с воздухом были выполнены сравнения распределений потенциалов для следующих типов моделей:
1) модель со всеми внутренними неоднородностями (НГК) и модели с единственной внутренней неоднородностью сравнивались с моделью без внутренних неоднородностей (модель однородной грудной клетки – ОГК). При этом во всех моделях учитывалась граница между ГК и воздухом.
2) модель ОГК и модели с внутренними неоднородностями и одной исключенной неоднородностью сравнивались с полной неоднородной моделью НГК. При этом во всех моделях присутствовала внешняя граница ГК с воздухом.
Дополнительно было выполнено сравнение распределений ПП, полученных в обоих типах моделей, с распределением потенциала точечного токового диполя, расположенного в безграничной однородной среде:
|
|
(6) |
где ![]() –
координаты точки на поверхности ГК;
–
координаты точки на поверхности ГК; ![]() – координаты
точечного токового диполя с проекциями вектора дипольного момента
– координаты
точечного токового диполя с проекциями вектора дипольного момента ![]() .
.
Для сравнения пары распределений потенциалов во всех случаях использовались следующие количественные характеристики:
– коэффициент корреляции Пирсона (КК)
|
|
(7) |
где 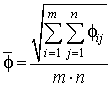 и
и 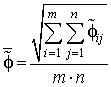 –
средние значения распределений
–
средние значения распределений ![]() и
и ![]() , заданных в виде матриц размерности
, заданных в виде матриц размерности ![]() ;
;
– относительное отклонение (ОО)
|
|
(8) |
где 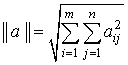 – норма матрицы.
– норма матрицы.
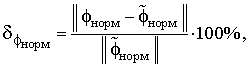
– относительное отклонение нормированных потенциалов (ООН)
|
|
(9) |
где  и
и
 – нормированные
распределения потенциалов;
– нормированные
распределения потенциалов;
– коэффициент масштаба (КМ), характеризующий отличие в диапазонах изменения ПП:
|
|
(10) |
– коэффициент сдвига (КС), показывающий отличие в средних уровнях ПП:
|
|
(11) |
Параметры КК и ООН позволяют сделать вывод относительно сходства или различия распределений потенциалов по форме, а остальные параметры – КМ и КС − позволяют выявить амплитудные отличия в распределениях. При известных значениях КМ и КС можно на основе (10), (11) перейти от максимального и минимального значения потенциалов в референтном распределении ПП к этим значениям в текущем распределении ПП.
Были рассчитаны распределения потенциала для
следующих моделей: диполь в однородной безграничной среде с проводимостью ![]() (БС); внутренне однородная модель
в форме эллиптического цилиндра с проводимостью
(БС); внутренне однородная модель
в форме эллиптического цилиндра с проводимостью ![]() с воздушной границей (ОГК);
неоднородная модель в форме эллиптического цилиндра с воздушной границей и
всеми внутренними неоднородностями с соответствующими им проводимостями (НГК);
модель ОГК с добавлением одной внутренней неоднородности – сердца, заполненного
кровью (ОГК+сердце), легких (ОГК+легкие), скелета (ОГК+скелет), мышц
(ОГК+мышцы), кожи и подкожного жира (ОГК+жир) в соответствии с рис. 1; полная неоднородная модель НГК и с исключенной
парциальной неоднородностью – сердцем (НГК-сердце), легкими (НГК-легкие),
скелетом (НГК-скелет), мышцами (НГК-мышцы), кожей и подкожным жиром (НГК-жир).
При этом проводимость области исключенной неоднородности равнялась проводимости
ОГК
с воздушной границей (ОГК);
неоднородная модель в форме эллиптического цилиндра с воздушной границей и
всеми внутренними неоднородностями с соответствующими им проводимостями (НГК);
модель ОГК с добавлением одной внутренней неоднородности – сердца, заполненного
кровью (ОГК+сердце), легких (ОГК+легкие), скелета (ОГК+скелет), мышц
(ОГК+мышцы), кожи и подкожного жира (ОГК+жир) в соответствии с рис. 1; полная неоднородная модель НГК и с исключенной
парциальной неоднородностью – сердцем (НГК-сердце), легкими (НГК-легкие),
скелетом (НГК-скелет), мышцами (НГК-мышцы), кожей и подкожным жиром (НГК-жир).
При этом проводимость области исключенной неоднородности равнялась проводимости
ОГК ![]() См/м.
См/м.
Для всех моделей токовый диполь располагался в
точке центра сферы сердца (см. рис. 1) с координатами
![]() м. Для всех
расчетов величина дипольного момента выбрана
м. Для всех
расчетов величина дипольного момента выбрана ![]() мА·м,
чтобы в модели БС разность потенциалов между точками (0, 0.18, 0.5) и
(0, –0.18, 0.5), соответствующими первому электрокардиографическому
отведению, составляла -2 мВ при ориентации вектора дипольного момента
мА·м,
чтобы в модели БС разность потенциалов между точками (0, 0.18, 0.5) и
(0, –0.18, 0.5), соответствующими первому электрокардиографическому
отведению, составляла -2 мВ при ориентации вектора дипольного момента ![]() вдоль линии плеч (ось OY).
вдоль линии плеч (ось OY).
Чтобы исключить влияние сдвига нуля потенциала при сравнении моделей, в каждой модели осуществлялась привязка нуля к точке с координатами (– 0.12, 0, 0.3333) м (соответствует центру спины на уровне диполя) путем вычитания потенциала в этой точке. Результаты сравнения моделей для различных ориентаций диполя представлены в таблицах 1 и 2, где обозначения моделей соответствуют приведенным выше.
Таблица 1. Сравнение распределений поверхностного потенциала различных моделей с однородной моделью в форме эллиптического цилиндра с воздушной границей (ОГК).
Фиолетовым цветом здесь и в табл. 2 отмечены ячейки с заметным отличием параметра сравниваемой модели, голубым цветом – ячейки с малым отличием.
|
Модель |
Ось
|
ОГК |
||||
|
|
% |
|
|
|
||
|
БС |
x |
6.0·10-3 |
3.314 |
0.445 |
0.636 |
0.636 |
|
y |
4.7·10-2 |
11.606 |
0.606 |
0.615 |
0.114 |
|
|
z |
1.5·10-1 |
23.422 |
0.774 |
0.570 |
-0.072 |
|
|
НГК |
x |
6.3·10-3 |
4.426 |
0.247 |
0.646 |
0.644 |
|
y |
6.1·10-3 |
3.612 |
0.459 |
0.583 |
0.926 |
|
|
z |
5.3·10-3 |
11.528 |
0.135 |
0.758 |
5.678 |
|
|
ОГК+сердце |
x |
8.7·10-6 |
0.206 |
0.428 |
0.568 |
8.7·10-6 |
|
y |
3.3·10-6 |
0.141 |
0.425 |
0.573 |
3.3·10-6 |
|
|
z |
2.0·10-6 |
0.170 |
0.427 |
0.571 |
2.0·10-6 |
|
|
ОГК+легкие |
x |
1.1·10-2 |
6.200 |
1.635 |
2.152 |
2.143 |
|
y |
6.1·10-3 |
3.281 |
0.649 |
0.364 |
0.270 |
|
|
z |
5.0·10-3 |
9.445 |
1.231 |
2.162 |
19.107 |
|
|
ОГК+скелет |
x |
8.1·10-4 |
1.663 |
0.068 |
0.884 |
0.882 |
|
y |
1.9·10-3 |
2.248 |
0.121 |
1.033 |
2.412 |
|
|
z |
4.5·10-4 |
3.585 |
0.062 |
0.961 |
0.827 |
|
|
ОГК+мышцы |
x |
5.5·10-4 |
0.512 |
0.099 |
1.107 |
1.107 |
|
y |
9.8·10-4 |
1.588 |
0.151 |
1.110 |
1.040 |
|
|
z |
5.3·10-4 |
3.653 |
0.100 |
1.129 |
-2.437 |
|
|
ОГК+жир |
x |
1.2·10-4 |
0.557 |
0.026 |
1.048 |
1.048 |
|
y |
5.2·10-5 |
0.540 |
0.034 |
1.049 |
1.033 |
|
|
z |
2.5·10-5 |
0.528 |
0.036 |
1.049 |
1.092 |
|
Таблица 2. Сравнение распределений поверхностного потенциала различных моделей с неоднородной моделью в форме эллиптического цилиндра с воздушной границей (НГК)
|
Модель |
Ось
|
НГК |
||||
|
|
% |
|
|
|
||
|
НГК-сердце |
x |
7.9·10-6 |
0.182 |
1.135 |
2.147 |
2.147 |
|
y |
1.2·10-6 |
0.051 |
1.236 |
2.234 |
2.234 |
|
|
z |
2.4·10-6 |
0.112 |
1.139 |
2.144 |
2.163 |
|
|
НГК-легкие |
x |
8.0·10-3 |
4.000 |
0.233 |
0.889 |
0.891 |
|
y |
1.3·10-2 |
5.921 |
0.399 |
1.190 |
1.982 |
|
|
z |
6.1·10-3 |
11.305 |
0.257 |
0.854 |
-0.244 |
|
|
НГК-скелет |
x |
2.0·10-3 |
2.313 |
0.226 |
1.186 |
1.187 |
|
y |
2.2·10-3 |
1.840 |
0.160 |
0.869 |
0.239 |
|
|
z |
1.6·10-3 |
6.819 |
0.127 |
1.042 |
0.779 |
|
|
НГК-мышцы |
x |
6.9·10-4 |
0.722 |
0.188 |
0.821 |
0.820 |
|
y |
5.5·10-4 |
0.986 |
0.232 |
0.780 |
0.796 |
|
|
z |
2.7·10-4 |
3.241 |
0.189 |
0.797 |
1.179 |
|
|
НГК-жир |
x |
3.4·10-4 |
0.895 |
0.073 |
0.901 |
0.901 |
|
y |
3.1·10-4 |
0.913 |
0.101 |
0.884 |
0.788 |
|
|
z |
6.8·10-5 |
0.607 |
0.091 |
0.899 |
0.862 |
|
|
ОГК |
x |
6.3·10-3 |
4.585 |
0.324 |
1.549 |
1.553 |
|
y |
6.1·10-3 |
3.632 |
0.837 |
1.715 |
1.080 |
|
|
z |
5.3·10-3 |
10.425 |
0.151 |
1.319 |
0.176 |
|
|
БС |
x |
1.8·10-2 |
7.793 |
0.305 |
0.986 |
0.988 |
|
y |
4.1·10-2 |
9.817 |
0.338 |
1.054 |
0.123 |
|
|
z |
2.0·10-1 |
30.907 |
0.772 |
0.752 |
-0.013 |
|
Анализ распределений потенциалов. Рассмотрим подробнее влияние отдельных неоднородностей на распределение поверхностного электрического потенциала (ПП).
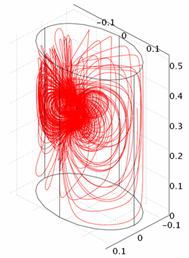
Влияние миокарда. Учет сердца, заполненного кровью, в модели ОГК уменьшает уровень
поверхностных потенциалов: в табл. 1 ![]() практически независимо от
ориентации диполя. Это связано с тем, что большая часть токов протекает в среде
с повышенным уровнем проводимости (кровь) и форма поверхности тела практически не
влияет на протекание токов (ср. рис. 2а и рис. 2б).
практически независимо от
ориентации диполя. Это связано с тем, что большая часть токов протекает в среде
с повышенным уровнем проводимости (кровь) и форма поверхности тела практически не
влияет на протекание токов (ср. рис. 2а и рис. 2б).
|
а) |
б) |
в) |
|
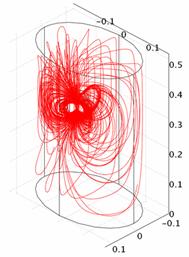
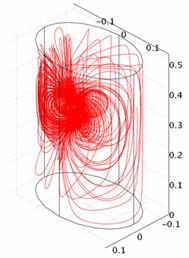
Рис. 2. Картины растекания токов вертикального диполя для различных моделей: а) ОГК; б) ОГК+сердце; в) ОГК+легкие. Оси соответствуют рис. 1 |
||
Наоборот, исключение данной неоднородности из
полной неоднородной модели (НГК) приводит к увеличению уровня ПП: ![]() в табл. 2.
В то же время учет сердца, заполненного кровью, практически не влияет на вид
КПП: на это указывают малые значения параметров
в табл. 2.
В то же время учет сердца, заполненного кровью, практически не влияет на вид
КПП: на это указывают малые значения параметров ![]() и
и ![]() как при сравнении моделей
ОГК+сердце и ОГК, так и при сравнении НГК-сердце и НГК.
как при сравнении моделей
ОГК+сердце и ОГК, так и при сравнении НГК-сердце и НГК.
Влияние мышц, жира и скелета. Добавление этих неоднородностей в модель однородной
грудной клетки (ОГК) незначительно сказывается на уровне потенциалов и на
форме карты поверхностных потенциалов (КПП): ![]() и
и ![]() . Однако можно отметить некоторое
уменьшение плотности токов у поверхности ГК в связи с пониженными значениями
удельной проводимости в этих тканях.
. Однако можно отметить некоторое
уменьшение плотности токов у поверхности ГК в связи с пониженными значениями
удельной проводимости в этих тканях.
Влияние легких.
Влияние легких в модели ОГК существенно зависит от ориентации диполя: при
ориентации вдоль проводящего промежутка между легкими (вдоль осей OX и OZ)
токи достигают поверхности ГК и уровень потенциалов, пропорциональный плотности
тока, возрастает (![]() ) по сравнению с
моделью ОГК, в которой значительная часть силовых линий токов замыкается во
внутренней среде ГК, не достигая поверхности ГК (ср. рис. 2а и
рис. 2в). При ориентации диполя перпендикулярно промежутку между легкими
значительная часть пространства перекрыта легкими для протекания токов и
поверхности ГК достигает малая часть токов (
) по сравнению с
моделью ОГК, в которой значительная часть силовых линий токов замыкается во
внутренней среде ГК, не достигая поверхности ГК (ср. рис. 2а и
рис. 2в). При ориентации диполя перпендикулярно промежутку между легкими
значительная часть пространства перекрыта легкими для протекания токов и
поверхности ГК достигает малая часть токов (![]() в табл. 1). Аналогично
прослеживается влияние неучета легких в неоднородной модели (ср. НГК-легкие и
НГК в табл. 2).
в табл. 1). Аналогично
прослеживается влияние неучета легких в неоднородной модели (ср. НГК-легкие и
НГК в табл. 2).
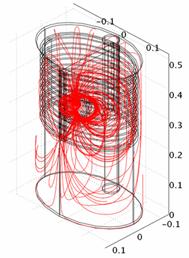
Однородная грудная клетка. Модель однородной грудной клетки (ОГК) по сравнению
с полной неоднородной моделью (НГК) дает повышенный уровень ПП (![]() , ср. рис. 3а и рис. 3б,
однако по форме КПП ближе к НГК, чем НГК без учета только легких (НГК-легкие):
для ОГК
, ср. рис. 3а и рис. 3б,
однако по форме КПП ближе к НГК, чем НГК без учета только легких (НГК-легкие):
для ОГК ![]() и
и ![]() %. Это связано с противоположным
влиянием отдельных неоднородностей в полной модели, особенно сердца и легких.
%. Это связано с противоположным
влиянием отдельных неоднородностей в полной модели, особенно сердца и легких.
|
а) |
б) |
|
Рис. 3. Картины растекания токов вертикального диполя для различных моделей: а) ОГК; б) полная НГК. Оси соответствуют рис. 1 |
|
Безграничная однородная среда. Что касается модели безграничной однородной
среды (БС), то она, имея схожий уровень ПП с НГК, дает существенные отличия в
форме КПП, особенно при вертикальной ориентации диполя: ![]() доходит до 0.2 (коэффициент
корреляции
доходит до 0.2 (коэффициент
корреляции ![]() ) и
нормированная погрешность – до уровня 30 %. Это связано с тем, что
сердечный диполь смещен от центра ГК в сторону груди (рис. 1б). Поэтому
грудная часть поверхности ГК в наибольшей степени препятствует симметричному
растеканию токов диполя, особенно при вертикальной ориентации и при ориентации
вдоль линии плеч (ось OY). Именно
этот фактор исключен из модели БС.
) и
нормированная погрешность – до уровня 30 %. Это связано с тем, что
сердечный диполь смещен от центра ГК в сторону груди (рис. 1б). Поэтому
грудная часть поверхности ГК в наибольшей степени препятствует симметричному
растеканию токов диполя, особенно при вертикальной ориентации и при ориентации
вдоль линии плеч (ось OY). Именно
этот фактор исключен из модели БС.
Качественное сравнение распределений потенциала на боковой поверхности ГК (рис. 1) для различных моделей может быть выполнено с помощью рис. 4. Здесь оцифровка шкалы псевдоцветов (в мВ) выбрана так, что границы диапазона для каждой карты ПП соответствуют минимальному и максимальному значению поверхностного потенциала. Из рис. 4 видно, что уровень изменения потенциала самый большой для модели ОГК при всех ориентациях диполя. Однако визуально более близки друг к другу карты ПП для моделей НГК и ОГК. Отмеченные особенности полностью согласуются с предыдущим анализом на базе табл. 1, табл. 2 и картин линий токов. Поскольку при ориентации диполя по оси OY он расположен симметрично относительно центрального сечения ГК (плоскость XOZ), то карты ПП для этого случая симметричны относительно нулевого уровня потенциала. Сравнивая результаты с данными работы [6], можно отметить сходство значений коэффициентов корреляции для различных видов неоднородностей, несмотря на различие моделей ГК и моделей возбуждения ПП.

В заключение следует отметить, что отдельные неоднородности (особенно это относится к легким и сердцу, заполненному кровью) могут существенно влиять на картину растекания токов дипольного источника и на уровень изменения поверхностных потенциалов. Однако, полная неоднородная модель, включающая различные неоднородности, имеет карту поверхностных потенциалов, близкую по форме к карте для однородной грудной клетки (коэффициент корреляции превышает уровень 0.99). Более того, полученные результаты подтверждают возможность использования представления о дипольном источнике в однородной безграничной среде при анализе ЭКГ сигналов в медицинской практике.
Литература
1. Титомир Л. И., Кнеппо П. Математическое моделирование биоэлектрического генератора сердца. – М.: Наука. Физматлит, 1999. – 447 с.
2. Einthoven, W. Weiteres uber das Elektrokardiogramm. // Pflüger Archiv fur die Gesamte Physiologie. 1908. V. 122. P. 517-548.
3. Geselowitz D.B. Dipole theory in electrocardiography. // Amer. J. of Cardiology. 1964. V. 14. Issue 3. P. 301-306.
4. Мурашко В.В., Струтынский А.В. Электрокардиография. − М.: МЕДпресс-информ, 2007. – 320с.
5. Лебедев В.В., Крамм М.Н., Жихарева Г.В., Иванов Г.Г., Попов Ю.Б. Система электродных отведений для измерения координат источников в области миокарда. // Медицинская техника. – 2006. – № 4. С. 7-9.
6. Klepfer R.N., Johnson C.R., MacLeod R.S.. The Effects of Inhomogeneities and Anisotropies on Electrocardiographic Fields: A Three-Dimensional Finite Element Study // IEEE Trans. Biomed. Eng. 1997. V. 44. N. 8. P. 706-719.
7. Wilson F.N., Вау1еу R.Н. The electric field of an eccentric dipole in а homogeneous spherical conducting medium //Circulation. 1950. V. 1. P. 84.
8. Rudy Y., Plonsey R. The eccentric spheres model as the basis for a study of the role of geometry and inhomogeneities in electrocardiography // IEEE Trans. Biomed. Eng. 1979. V. 7. P. 392.
9. Yeh G.C.K., Martinek J. The potential of a general dipole in a homogeneous conducting prolate spheroid. // Ann. N. Y. Acad. Sci. 1957. V. 65. N. 6. P. 1003-1006.
10. Berry P.M. N, M space harmonics of the oblate spheroid // Ann. N. Y. Acad. Sci. 1957. V. 65. N. 6. P. 1126-1134.
11. Frank E. The Zero-Potential Contour on a Homogeneous Conducting Cylinder. IRE Trans. Med. Electron. 1, 27 (1953).
12. Burger H.C., Tolhoek H.A., Backbier F.G. The potential distribution on the body surface caused by a heart vector. // Amer. Heart. J. 1954. V. 48. N. 2. P. 249-263.
13. Стрелков Н.О., Жихарева Г.В., Крамм М.Н. Влияние параметров грудной клетки на результаты реконструкции эквивалентного токового диполя сердца. // Материалы XXII международной конференции “Биотехнические, медицинские и экологические системы и комплексы. Биомедсистемы – 2009”. – Рязань: РГРТУ, 2009 – 560 с. С. 201-204.
14. Стрелков Н.О., Жихарева Г.В. Сравнение моделей грудной клетки для решения прямой и обратной задач ЭКГ // Сборник статей IV Всероссийской научно-технической конференции "Информационные и управленческие технологии в медицине и экологии". - Пенза: Приволжский Дом знаний, 2010. – 152 с. С. 120-122.
15. Bergman R.A., Afifi A.K., Jew J.Y., Reimann P.C.. Atlas of Human Anatomy in Cross Section. – München: Urban & Schwarzenberg, 1991. – 426 p.