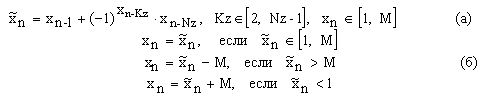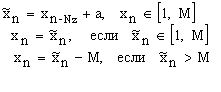УДК 621.391

РАЗРАБОТКА И ИССЛЕДОВАНИЕ СЛОЖНЫХ ХАОТИЧЕСКИХ СИГНАЛОВ ДЛЯ ИСПОЛЬЗОВАНИЯ В ШИРОКОПОЛОСНЫХ ИНФОРМАЦИОННЫХ ЦИФРОВЫХ ТЕХНОЛОГИЯХ

Р. В. Беляев, В. В. Колесов

Институт радиотехники и электроники им. В.А.Котельникова РАН

Получена 20 июля 2012 г.

 

Аннотация. Для эффективного применения широкополосных информационных цифровых технологий в радиолокационных и гидролокационных системах, а также в системах связи, навигации и позиционировании объектов необходима разработка псевдослучайных кодирующих последовательностей большой длительности. В работе на основе хаотического порождающего дискретного алгоритма с запаздыванием, заданном на ограниченном интервале, в многомерном фазовом пространстве исследованы свойства дискретной целочисленной динамической системы. Численным экспериментом показано, что при надлежащем выборе параметров порождающего алгоритма такая система обладает всеми свойствами динамического хаоса и способна формировать непрерывную псевдослучайную целочисленную последовательность большой длины: порядка N=10¹² и более.

Ключевые слова: широкополосные информационные технологии, динамический хаос, хаотические сигналы, порождающие алгоритмы, псевдослучайные последовательности.

Abstract: For the effective application of wide-band information digital technologies in the radar and sonar systems, and also in the systems of communications, navigation and positioning of objects it is necessary the development of the pseudorandom coding sequences of large duration. In the work on the basis of the chaotic generating discrete algorithm with the delay, assigned in the limited interval, in the multidimensional phase space the properties of discrete integral dynamic system are investigated. The numerical experiment showed that with the proper selection of the parameters of the generating algorithm this system possesses all properties of dynamic chaos and is capable of forming the continuous pseudorandom integral sequence of the large length: the order of N=10¹² and more.

Key words: wide-band information technologies, dynamic chaos, chaotic signals, generating algorithms, pseudorandom sequences.

 

ВВЕДЕНИЕ

Поиск информационных носителей (процессов и сигналов), обладающих повышенной информационной емкостью, и математических алгоритмов, порождающих такие процессы, является наиболее актуальной задачей при разработке новых информационных технологий [1]. К информационным системам относятся все устройства, обеспечивающие получение, обработку, передачу и хранение информации. Это различные датчики, преобразующие внешние воздействия (звук, изображение в виде светового поля различной локальной интенсивности, давление, температура, химический состав среды и др.) в электрические сигналы, электронные системы преобразования и обработки этих сигналов на основе компьютерной техники, это средства радиосвязи и телекоммуникаций. Информация в этих системах записывается либо в виде непрерывного электрического сигнала- аналоговая форма кодирования информации, либо в виде последовательности электрических импульсов- цифровая форма кодирования. При аналоговом кодировании необходимая информация передается при манипуляции параметрами непрерывного электрического сигнала. В цифровой форме информация выражается в виде двоичного кода, задаваемого электрическим импульсом, для которого, например, логическому состоянию"0" соответствует отсутствие электрического напряжения (или тока), а состоянию "1"- его наличие. Цифровые коды благодаря хорошей защищенности от ошибок и помех, высоким скоростям обработки в вычислительных системах и высокой плотности передачи по каналам связи преимущественно распространены в современных информационных системах.

Прикладное применение информационных технологий предполагает физическую реализацию конкретного кодирующего процесса при передаче, обработке и хранении информации в телекоммуникационных системах и компьютерных сетях. Прогресс в данной области связан с увеличением быстродействия и повышением помехозащищенности информационных каналов.

Проблема защиты информации в открытых информационных каналах и компьютерных сетях, а также задача повышения помехоустойчивости телекоммуникационных каналов связаны с применением сложных кодирующих алгоритмов и шумоподобных сигналов с большой информационной емкостью. Поэтому разработка сложных кодирующих алгоритмов и критериев объективной оценки их статистических свойств является достаточно актуальной [2].

Для целей кодирования информации очень перспективно применение псевдослучайных последовательностей (ПСП) целых чисел, подобных известным [3] последовательностям Фибоначчи x_n=(x_n-1+x_n-Nz)mod(M) в ограниченном объеме фазового пространства (ФП). После применения необратимой операции клипирования такая последовательность превращается в непериодическую бинарную последовательность, обладающую высокой стойкостью к возможности предсказания ее поведения и раскрытию формулы порождающего алгоритма. В то же время последовательности такого типа вследствие детерминированности используемых преобразований и действий на поле целых чисел могут быть воспроизведены совершенно точно на любом вычислительном устройстве.

Класс целочисленных детерминированных псевдослучайных сигналов с динамическим хаосом, воспроизводимых с высокой точностью на любом компьютере, делает проблему взаимной синхронизации устройств с динамическим хаосом простой и естественной, и является достаточно перспективным для применения в телекоммуникационных системах для потокового кодирования информации [4].

Несмотря на достаточно простой алгоритм, дискретная динамическая система с хаосом при определенных условиях формирует псевдослучайный процесс с хорошими статистическими свойствами. Необходимо отметить, что после применения операции клипирования многоуровневого псевдослучайного процесса задача восстановления исходной формулы порождающего алгоритма практически становится невыполнимой. Таким образом реализуется высокая криптостойкость кодирования информации. При этом можно в достаточно широких пределах менять значения параметров алгоритма, такие как область определения и, главное, размерность фазового пространства. Тем самым имеется возможность в широких пределах изменять статистические и корреляционные свойства формируемого данным алгоритмом псевдослучайного процесса.

ФАЗОВОЕ ПРОСТРАНСТВО АЛГОРИТМА

В качестве тестируемого рассмотрен хаотический алгоритм с запаздыванием, формирующий псевдослучайную последовательность (ПСП) целых чисел, определенный на конечном замкнутом интервале натурального ряда [1, М], M>1 [5]:

(1)

Здесь Nz - параметр запаздывания, определяющий размерность фазового пространства (ФП) алгоритма, а число Kz выбирается из целочисленного интервала задержки [1,Nz].

Основным в алгоритме является отображение типа Фибоначчи (1а), а операция преобразования интервала [1,M] самого в себя с "отражающими границами" (1б) ограничивает объем ФП данной дискретной динамической системы (ДС). ФП представляет собой конечное множество из N_ФП=M^Nz точек возможных состояний системы с координатами (x_-1,x_-2,… x_-Nz) и соответствующим радиус-вектором . В зависимости от выбора начальных условий  ДС (1) на каждом шаге алгоритма (итерации) дискретно переходит из одного своего состояния в другое, из одной точки ФП в другую. Здесь осуществляются только дискретные переходы, для наглядного представления которых можно проводить лишь условные "траектории", показывающие направление и длину ΔR перехода. Из-за ограниченности объема ФП движение системы (1) происходит по замкнутым "траекториям"- циклам, которые, вследствие однозначности используемых преобразований, не имеют общих точек. Все точки ФП принадлежат только одному определенному циклу, либо являются изолированной точкой с координатами (M,M,… M). Так, например, при Nz=4, Kz=3, M=5 в ФП алгоритма присутствует один 562-тактный цикл, два цикла с периодом N_p=27, один 8-тактный цикл и одна особая точка. При Nz=5, Kz=3 и M=13 (M^Nz=371293) в ФП существуют циклы с периодами N_p =332373, 21721, 7966, 4959, 3640, а при Nz=6, Kz=4 и M=15 один "длинный" цикл с периодом N_p=11099897 включает в себя подавляющее большинство (0.974·M^Nz) точек ФП.

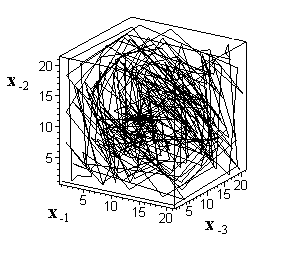
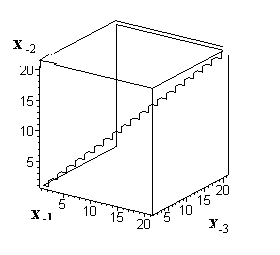
Введем следующие определения. Цикл с переходами между соседними состояниями, имеющими случайную длину и направление, назовем псевдослучайным циклом (ПСЦ). Цикл же с регулярными переходами будем называть регулярным циклом (РЦ) [6]. Циклы алгоритма (1) имеют важную отличительную особенность: поведение динамической системы на цикле до его замыкания имеет случайный, хаотический характер (Рис.1), а порождаемая при этом алгоритмом непериодическая последовательность {x_n} длиной N<N_p имеет псевдослучайный характер. Множество точек состояний динамической системы в ФП, объединенных в такой цикл, образуют псевдослучайный цикл. В отличие от регулярного цикла, простой пример которого в 3-мерном пространстве приведен на Рис.2а. Этот цикл является одним из 147 циклов с периодом N_p=63 отображения (2) с параметрами Nz=3, a=1, M=21.

(2)

Таким образом, псевдослучайный цикл представляет собой конечное множество внешне хаотически, но строго детерминированным образом следующих одна за другой точек состояний дискретной ДС в ФП алгоритма.

Рис.1. Фазовый портрет 290 точек цикла алгоритма (1) с параметрами Nz=3, Kz=2, M=21, R0(1,1,1), период цикла Nп=4340.	Рис.2а Фазовый портрет цикла алгоритма (2) c параметрами Nz=3, a=1, M=21, R0(1,1,1), период цикла Np=63.

 

Пример более сложного регулярного цикла приведен на Рис.2б:

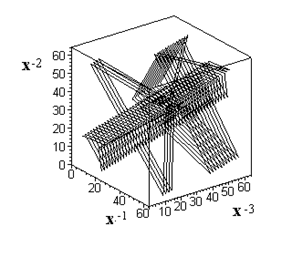
Рис.2б Фазовый портрет цикла, формируемого тем же алгоритмом (2) c параметрами Nz=3, a=2, M=63.

 

Механизм динамического хаоса

Причины хаотического поведения системы (1) до замыкания цикла укладываются в общие представления о механизме, приводящему к динамическому хаосу. Этот механизм достаточно универсален. Два его основных элемента- растяжение и складывание- являются главными свойствами любого хаотического отображения [7]. В общем случае нелинейного отображения интервала [1,M] в себя имеет место комбинация растяжений и складывания, которая постоянно возвращает итерации начальной точки на интервал [1,M] каждый раз на разную заранее непредсказуемую величину, что и ведет к хаотическому поведению динамической системы.

В отличие от динамических систем с непрерывным временем в случае дискретной ДС непрерывная траектория движения отсутствует. Система эволюционирует дискретными скачками, заданными на поле целых чисел. Тем не менее по аналогии с непрерывными ДС, можно показать, что отображение (1а) обеспечивает растягивающие преобразования в движении исследуемой дискретной системы. Для этого исследуем изменение расстояний DR(n)=function(n) в ФП между соседними точками состояний на "траектории" движения анализируемой целочисленной дискретной ДС. Это, по-видимому, самая близкая аналогия по отношению к непрерывным системам, т.к. анализируется расстояние между самыми близкими траекториями, которые проходятся системой с отставанием во "времени" на одну итерацию.

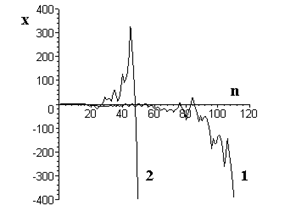
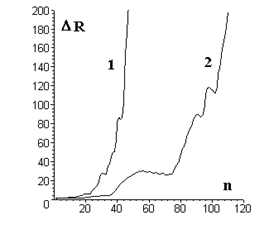
На рис.3 и рис.4 показаны графики изменения значений чисел x(n), генерируемых отображением (1а) в неограниченном объеме фазового пространства на множестве целых положительных и отрицательных чисел (x Î [-∞,+∞]), и соответствующие изменения расстояний ΔR между соседними состояниями при значениях параметров отображения Nz=5, Kz=3, и Nz=16, Kz=9. В обоих случаях в качестве начального выбирался вектор с координатами, равными единице.

 

Рис.3. Последовательность чисел, генерируемых отображением (1а) в неограниченном ФП.	Рис.4. Соответствующие изменения расстояний ΔR между соседними состояниями.
Значения параметров Nz=5, Kz=3, R0(1,1,1) (кривые 1) и Nz=16, Kz=9, R0(1,1,…1) (кривые 2).

 

Эти данные показывают, что отображение (1а) обуславливает расходимость, в среднем по экспоненциальному закону, движения динамической системы в неограниченном ФП. При этом следует подчеркнуть, что определяющим фактором здесь является не столько экспоненциальное увеличение генерируемых чисел x(n), сколько экспоненциально нарастающий вид зависимости ΔR(n). Например, для регулярного цикла, показанного на рис.2, график x(n) в неограниченном ФП также является монотонно возрастающей функцией, но изменения длины переходов между состояниями при этом не наблюдается: ΔR(n)=Const=1.

Таким образом, аналогом экспоненциального расхождения бесконечно близких траекторий динамических систем с непрерывным временем в системах с дискретным временем можно считать экспоненциальное увеличение расстояний между соседними состояниями, что при наличии в алгоритме преобразований, ограничивающих объем ФП, приводит к перемешиванию и хаотизации движения системы в фазовом пространстве.

Если при отражении от границ ФП, что в алгоритме обеспечивается преобразованиями (1б), дискретная система в результате "складывания" в интервал [1,M] попадает в новое состояние, то хаотическое движение продолжается. Если же система при этом попадает в одно из прежних состояний, то вследствие однозначности преобразований цикл замыкается и далее система идет по кругу.

Вид зависимости ΔR(n) в (неограниченном ФП) и характер (дискретных) распределений вероятностей p(ΔR_i) по множеству {ΔR_i} всех возможных длин переходов между состояниями уже в ограниченном объеме ФП алгоритма позволяет более точно отнести конкретный цикл к разряду псевдослучайных или же регулярных. Необходимо отметить, что, как показывает численный эксперимент, для хаотического движения дискретной ДС вид зависимости ΔR(n) не обязательно должен быть экспоненциальным, достаточно уже его линейного роста с большой крутизной.

 

 

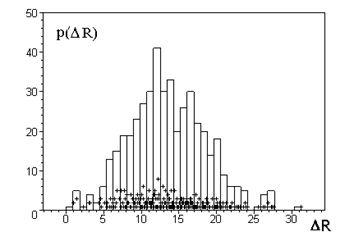
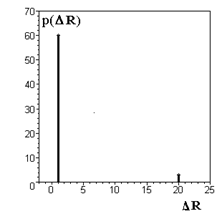
Рис.5. Распределение и гистограмма длин и переходов между точками цикла алгоритма (1) с параметрами Nz=3, Kz=2, M=21, R0(1,1,1), период цикла Np=4340.	Рис.6. Распределение длин переходов цикла алгоритма (2) c параметрами Nz=3, a=1, M=21, R0(1,1,1), период цикла Np=63.

 

Простыми критериями стохастичности дискретного алгоритма в совокупности являются: вид основных преобразований алгоритма, характер поведения ДС на цикле (фазовый портрет или его проекции меньшей размерности), вид функции распределения вероятностей длин переходов на цикле, когда в распределении p(ΔR) присутствуют практически все возможные длины переходов (рис.5) или же такого не наблюдается (рис.6), а также непосредственный анализ формируемой алгоритмом последовательности.

КРИТЕРИЙ СУЩЕСТВОВАНИЯ ПСЦ В ОДНОМЕРНОМ И ДВУМЕРНОМ ПРОСТРАНСТВЕ

Рассмотрим одномерный алгоритм (одномерное ФП) [8]:

,                                                                  (3)

 

с параметрами: a=10, c=0, x₀=7, М=2551.

На следующем рисунке представлена реализация процесса {x_n}, генерируемого данным алгоритмом

 

Рис.7. Реализация последовательности, формируемая алгоритмом (3), М=2551.

 

Из рисунка видно, что система формирует псевдослучайную последовательность. При этом преобразование (3) в неограниченном ФП демонстрирует не экспоненциальное, а чисто линейное возрастание расстояний между соседними состояниями DR.

Хаотическое поведение ДС в двумерном пространстве можно исследовать на примере генератора типа Фибоначчи, дополненного операцией отражения от границ:

                                      (4)

 

Сначала проанализируем поведение данной дискретной ДС с параметром М=25. В этом случае фазовое пространство алгоритма объемом V_ФП=625 состоит их непересекающихся 5 циклов с периодом N_p=100, 6 циклов с периодом N_p=200, одного 4-тактного цикла и одной изолированной точки.

На следующем рисунке представлена реализация процесса {x_n}, генерируемого алгоритмом с начальным вектором R₀(1,1). Из графика видно, что система находится на цикле с периодом N_p=100, а поведение ДС внутри цикла до его замыкания хаотично. Что, естественно, т.к. преобразование Фибоначчи в неограниченном ФП демонстрирует экспоненциально возрастающее увеличение расстояний между соседними состояниями DR.

 

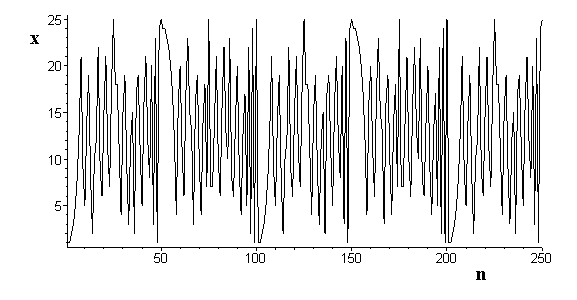
Рис.8. Реализация последовательности, формируемая алгоритмом (3), М=25.

 

На Рис.9 представлен фазовый портрет данного цикла:

Рис.9. Фазовый портрет цикла с периодом N_p=100.

 

На рисунке приведены условные траектории, которые показывают порядок и направления переходов анализируемой дискретной ДС.

Проведем аналогичное численное исследование поведения системы при большем объеме фазового пространства: Nz=2, М=255, V_ФП =65025. В этом случае спектр циклов в фазовом пространстве следующий: N_p=360(128), 180(32), 72(160), 40(4), 36(4), 20(1), 8(5), Т4(1), Т1(1). (В круглых скобках указана кратность соответствующих циклов). Реализация процесса с начальным вектором (1,1) показана на рис. 10.

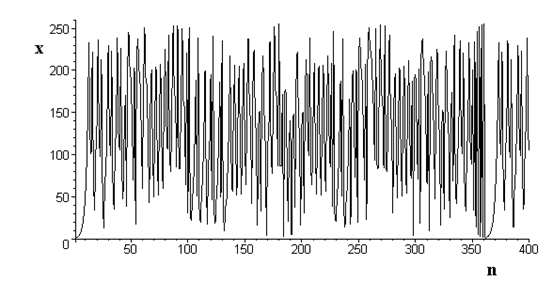
Рис.10. Реализация последовательности, формируемая алгоритмом (3), М=255, N_p=360.

 

Поведение системы до замыкания цикла вполне хаотическое. Исследуем зависимость DR(n):

 

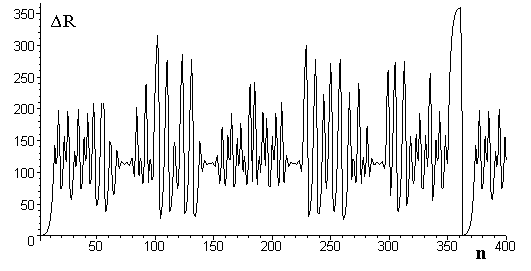
Рис.11. Изменения расстояний между точками цикла N_p=360.

 

Учитывая, что наибольшее расстояние между состояниями системы в данном случае равно sqrt(2*254^2)=359, видно, что разброс расстояний между точками на цикле происходит на всю доступную область фазового пространства. Фазовый портрет исследуемого псевдослучайного цикла показан на рис.12.

 

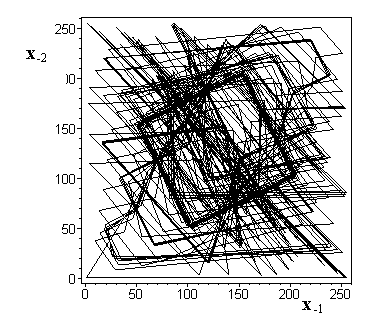
Рис.12. Фазовый портрет цикла N_p=360.

 

Таким образом, можно сделать вывод, что в двумерном ФП могут существовать ПСЦ, но, статистические свойства формируемого хаотического процесса далеки от идеального. Например, на представленном, на рис.12 фазовом портрете наблюдаются несколько аттракторов, а не семейство полностью случайных скачков, как это происходит в случае ПСЦ большой размерности с некоррелированной последовательностью.

 Плотность распределения вероятностей

Как показал анализ, формируемые алгоритмом (1) ПСП на длинном (N_p/N_ФП ~0.3) псевдослучайном цикле, по своим статистическим свойствам близки к последовательности с равномерным распределением вероятностей генерируемых чисел p(x). Количественные результаты приведем для алгоритма (1) с параметрами: Nz=16, Kz=9 и M=255.

Принимая во внимание, что

{x_n} - последовательность чисел x_i (x_i Î [1, М]), n=1,2,3…N.

N - длина последовательности,

n_i - количество чисел x_i в реализации последовательности длиной N,

{p_i=n_i/N}] - массив частот появления числа x_i на длине реализации N,

{p₌=1/M] - плотность равномерного распределения вероятностей,

обозначим среднее по модулю отклонение частот p_i от равномерного распределения как:

наибольшее по модулю отклонение частот p_i от равномерного:

,

и среднеквадратичное отклонение частот p_i от равномерного распределения как:

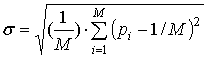
На Рис.13 приведены графики отличий распределений от равномерного на различных длинах N анализируемой ПСП, формируемой алгоритмом (1):

 

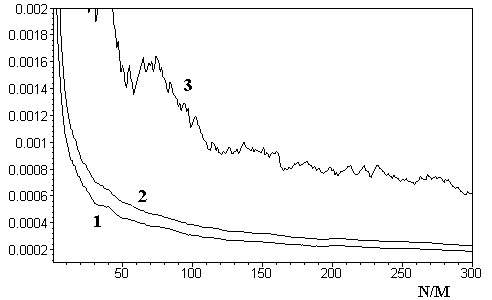
Рис.13. 1) Dp_ср, 2) s, 3) Dp_макс.

 

Сопоставим полученные результаты с аналогичными для последовательностей формируемых генератором случайных чисел RND математического пакета Maple:

 

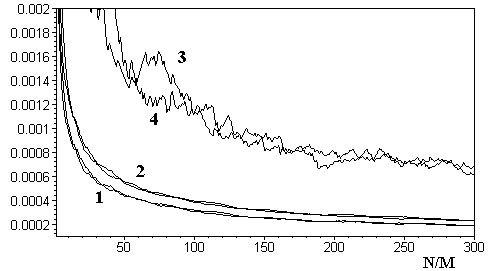
Рис.14. 1) Dp_ср, 2) s, 3) Dp_макс, 4) Dp_макс (RND).

 

Из сопоставления хода зависимостей для алгоритма (1) и генератора RND видно, что результаты фактически идентичны.

В Таблице 1 приведены результаты численного эксперимента по сопоставлению отличия от равномерного распределения p₌=1/M распределений вероятностей чисел, формируемых алгоритмом (1) (Nz=16, Kz=9, M=255) и генератором случайных чисел RND-Maple (трансформированного к генерации целых чисел на интервале [1,255]):

 

Таблица 1

Среднее по модулю Dp_ср, среднеквадратичное s и максимальное Dp_макс отклонение частоты появления чисел в ПСП относительно равновероятного значения (1/M)

	N/M	50	100	150	200	250	300
Dpср /p=	RND и алгоритм(1)	0.11	0.08	0.07	0.065	0.055	0.05
s/p=	RND и алгоритм(1)	0.14	0.10	0.08	0.07	0.065	0.06
Dpмакс/p=	RND	0.36	0.29	0.22	0.19	0.18	0.18
	Алгоритм(1)	0.39	0.29	0.23	0.20	0.19	0.17

 

Из приведенных данных следует, что распределения вероятностей для ПСП, сформированных алгоритмом (1) и генератором RND очень близки: разница между этими генераторами по относительной величине отличия плотности распределения от равновероятного значения не более 1% при длине реализации N>100×M. 

Сверхдлинные ПСП

Для практических применений наибольший интерес представляют непериодические псевдослучайные последовательности большой длины. При надлежащем выборе параметров алгоритма (1) и начальных условий сегмент непериодической ПСП, формируемой алгоритмом на псевдослучайном цикле до выхода системы на период, может быть произвольно большой длины и, как показал анализ, по своим статистическим свойствам близок к последовательности с равномерным распределением вероятностей генерируемых чисел p(x). Для подтверждения этого было проведено численное моделирование по определению периода ПСП, формируемой алгоритмом (1) при сравнительно небольших (по сравнению с возможными и практически значимыми) объемах ФП. Поскольку в ФП алгоритма при любых значениях параметров и начальных условий (кроме, конечно, (М,М,…М)) могут существовать только циклы, то признаком выхода системы на период является простое повторение начальных условий, т.е. вектора начального состояния. Для численного эксперимента были выбраны следующие параметры алгоритма: Nz=3, 5, 7, 9 и М=63 так, чтобы в течение реального времени достигнуть замыкания цикла. В качестве начальных условий каждый раз выбирался вектор с координатами, равными единице. Получены следующие результаты:

1) Nz=3, M=63, N_ФП=2.50047*10⁵, найденный период цикла N_з=7.8317*10⁴, N_p/N_ФП=0.31,

2) Nz=5, M=63, N_ФП=9.9243365*10⁸, период цикла N_п=3.3174*10⁸, N_p/N_ФП =0.33,

3) Nz=7, M=63, N_ФП=3.93898*10¹², найденный период N_p=1.676*10¹², N_p/N_ФП =0.425,

4) Nz=9, M=63, N_ФП=1.56338*10¹⁶, замыкания цикла не достигнуто за 4.518*10¹² итераций.

Следовательно прямым численным экспериментом показано, что с помощью анализируемого алгоритма с запаздыванием (1) можно формировать непериодические последовательности с длиной, большей, чем N=4.5*10¹² целых чисел. При выборе соответствующих начальных условий на длинном цикле следует ожидать, что длина непериодической ПСП может быть порядка 0.3*M^Nz [9].

 ЗАКЛЮЧЕНИЕ

Таким образом, показано, что исследованный порождающий алгоритм, формирует псевдослучайные последовательности большой длины и может быть эффективно использован в телекоммуникационных системах для потокового кодирования информации, обеспечивая необходимую помехоустойчивость и криптостойкость. При этом семейство целочисленных детерминированных хаотических алгоритмов воспроизводится на любой вычислительной платформе и делает проблему взаимной синхронизации устройств с динамическим хаосом простой и естественной, и является достаточно перспективным для применения в широкополосных цифровых технологиях.

Работа выполнена при финансовой поддержке Минобрнауки ГК № 07.514.11.4080 и 14.740.11.0645.

 

Литература

1.       Гуляев Ю.В., Беляев Р.В., Воронцов Г.М., Залогин Н.Н., Калинин В.И., Кальянов Э.В., Кислов В.В., Кислов В.Я., Колесов В.В., Мясин Е.А., Чигин Е.П., Информационные технологии на основе динамического хаоса для передачи, обработки, хранения и защиты информации, Радиотехника и электроника, 2003г., т.48, № 10. С. 1157-1185.

2.       Р.В. Беляев, Г.М. Воронцов, В.Я. Кислов, В.В. Колесов, С.В. Крупенин, А.М. Попов, В.И. Рябенков, Сложные хаотические дискретные сигналы в системах телекоммуникации, радиолокации и навигации, Радиотехника и электроника, 2006г., т.51, № 9. С. 1116-1128.

3.       Кнут Д. Искусство программирования для ЭВМ. Получисленные алгоритмы. Т.2. Пер. с англ. М.: Мир, 1977.

4.       Kolesov V.V., Potapov A.A., The Information Technologies on Dynamic Chaos for Telecommunication, Radar and Navigation Systems, Electromagnetic Phenomena, V5, N2(15), 2005, P 89-104.

5.       Kolesov V.V., The phase space of the digital encoding algorithm for telecommunication systems, 14th Int. Crimean Conference “Microwave & Telecommunication Technology” (Crimico’2004), 13-17 September 2004, Sevastopol, Crimea, Ukraine, Proceedings, P.306-307.

6.       Ryabenkov V.I., Kolesov V.V., Belyaev R.V., Popov A.M., The structured characteristics of the pseudorandom sequences, formed by discrete algorithm with delay, 7th International Conference and Exhibition on digital signal processing and its applications, DSPA`2005, 16-18 March, 2005, Moscow, Russia, Proceedings, V.1, P. 7-11.

7.       Г.Шустер Детерминированный хаос: Введение — М.: Мир, 1988. — 240 с.

8.       Kolesov V.V., The chaotic encoding algorithm on the basis of two-dimensional mapping, 14th Int. Crimean Conference “Microwave & Telecommunication Technology” (Crimico’2004), 13-17 September 2004, Sevastopol, Crimea, Ukraine, Proceedings, P. 294-295.

9.       R.V.Belyaev, G.V.Vorontsov, N.N.Zalogin, V.V.Kolesov, The largest period of pseudo-random sequence forming by discrete algorithm with delay, The 3st International Conference and Exhibition “Digital Signal Processing and its Applications (DSPA-2000), 22-24 November 2000, Moscow, Russia, Abstracts of reports, P 53-57.