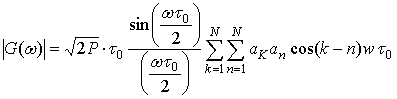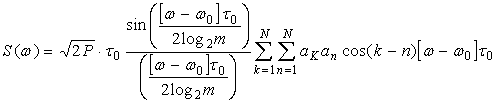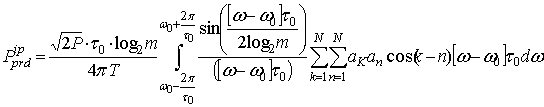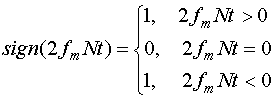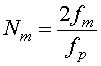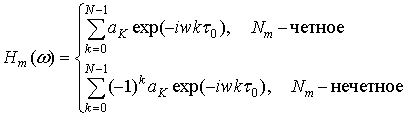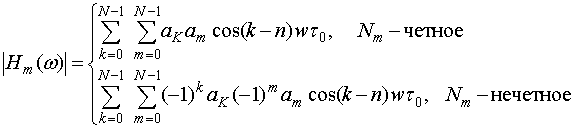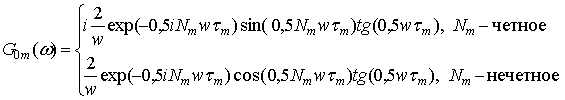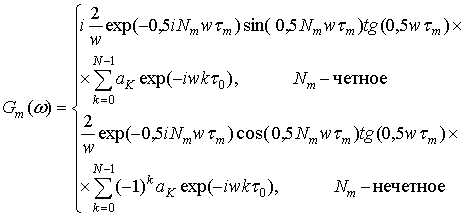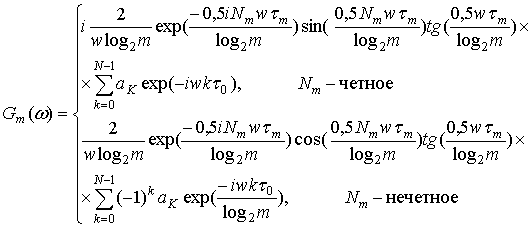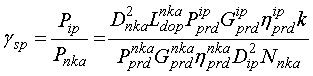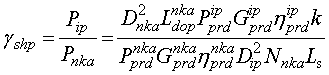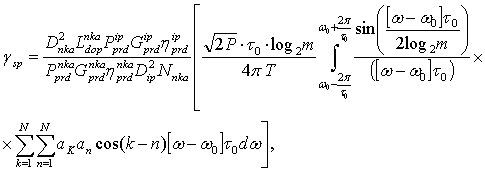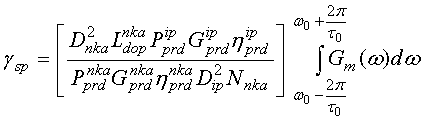ОЦЕНКА ЭФФЕКТИВНОСТИ ПОДАВЛЕНИЯ СИГНАЛОВ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ ПРЕДНАМЕРЕННЫМИ ПОМЕХАМИ
А. А. Кащеев, В. И. Кошелев
ФГБОУ ВПО «Рязанский государственный радиотехнический университет»
Получена 26 июня 2012 г.
Аннотация. Рассмотрены математические модели преднамеренных помех спутниковым радионавигационным системам (СРНС) ГЛОНАСС, GPS и Galileo. По критерию отношения помеха-сигнал на выходе коррелятора наземной аппаратуры потребителя проведена оценка эффективности подавления сигналов СРНС ГЛОНАСС, GPS и Galileo структурными и шумовыми помехами.
Ключевые слова: спутниковые радионавигационные системы; преднамеренные помехи; меандровые шумоподобные помехи; структурные помехи; наземная аппаратура потребителя.
Abstract. Mathematical models of the intentional hindrances satellite radio navigational system (SRNS) GLONASS, GPS and Galileo are considered. The estimation of efficiency of the suppression of signal SRNS GLONASS, GPS and Galileo structured and noise hindrance is made according to criterion of relations hindrance-signal on the correlator output of the overland equipment of the consumer.
Keywords: the satellite radio navigational systems; the intentional hindrances; the noise-like meanders hindrances; the structured hindrances; the overland equipment of the consumer.
Введение
В условиях информационного конфликта актуальной задачей является разработка эффективных средств подавления радионавигационных систем и средств их защиты, обеспечивающих возможность функционирования аппаратуры потребителей (АП) навигационных систем при действии помех в области расположения АП. Для разработки таких средств защиты необходимо исследовать характер и степень влияния помех на АП.
Целью работы является сравнительная оценка влияния преднамеренных помех различного вида на эффективность подавления сигналов СРНС ГЛОНАСС, GPS и Galileo.
Математические модели преднамеренных помех
Преднамеренные помехи, формируемые спутниковым радионавигационным системам, условно можно разделить на структурные и шумовые [1, 2].
Структурные помехи повторяют структуру спутникового навигационного сообщения форматов ГЛОНАСС, GPS или Galileo и могут содержать или не содержать произвольных данных о местонахождении объекта. К числу таких помех можно отнести: помехи с фазовой манипуляцией, модулированные М-последовательностью (ПФМП) или кодом Голда (ПФМГ); меандровые шумоподобные помехи (МШП).
Помехи ПФМП и ПФМГ. Помеха с фазовой манипуляцией, модулированная М-последовательностью, по своей структуре подобна сигналам СРНС ГЛОНАСС, которую математически можно представить следующим образом [3]:
|
|
(1) |
где 
-
мощность помехи сигналу i-го спутника ГЛОНАСС; 
-
данные i-го спутника ГЛОНАСС, учитываемые при формировании помехи; 
- код спутника ГЛОНАСС; 
- круговая частота i-го спутника
ГЛОНАСС, соответствующая частоте L1 с учетом доплеровского
сдвига; 
- круговая частота i-го спутника
ГЛОНАСС, соответствующая частоте L1 с учетом доплеровского сдвига; 
- начальный фазовый сдвиг.
Помеха с фазовой манипуляцией, модулированная кодом Голда, по своей структуре подобна сигналам СРНС GPS, математическое описание которой имеет вид [3]:
|
|
(2) |
|
|
где 
-
помеха сигналу i-го спутника GPS; t - системное время соответствующего
спутника; 
- мощность синфазной составляющей i-го
спутника GPS; 
-
данные i-го спутника GPS; 
- С/А-код i-го
спутника GPS; 
- круговая частота спутника
GPS, соответствующая частоте L1 с учетом доплеровского сдвига; 
- начальный фазовый сдвиг; 
- мощность квадратурной составляющей i-го
спутника GPS; 
- P-код i-го спутника GPS; 
- круговая частота спутника GPS,
соответствующая частоте L2 с учетом доплеровского сдвига; 
- круговая частота спутника GPS,
соответствующая частоте L5 с учетом доплеровского сдвига
Рассматривая ПФМГ и ПФМП
как суммарное произведение прямоугольных импульсов с единичной амплитудой и
длительностью 
и кодовой последовательностью A
= (a1 a2… aN), комплексную огибающую
спектра помехи можно представить как [4, 5]:
|
|
(3) |
где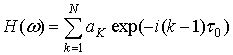 
- спектр кодовой
последовательности A;
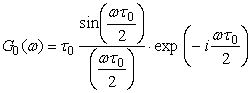- спектр
прямоугольного импульса;
- длительность
прямоугольного импульса.
Здесь коэффициенты ak являются элементами кодовой последовательности A, которая представляет собой М-последовательность для ПФМП или код Голда – для ПФМГ.
Амплитудный спектр ПФМП и ПФМГ является модулем от спектра комплексной огибающей спектра помехи, который после преобразования выражения (3) приобретает следующий вид:
|
|
(4) |
Так как помеха
представляет собой фазоманипулированное колебание с частотой 
, спектр помехи в окончательном виде может
быть представлен как:
|
|
(5) |
Приведенное выражение позволяет оценить только спектральную плотность мощности помехи с двухпозиционной фазовой манипуляцией. С учетом того, что ПФМП и ПФМГ имеет характер многократной фазовой манипуляции, выражение (5) можно представить следующим образом:
|
|
(6) |
Учитывая выражение (6), среднюю мощность передатчика источника помех с многократной фазовой манипуляцией можно представить как:
|
|
Помехи МШП. Меандровые шумоподобные помехи по своей структуре идентичны сигналам СРНС Galileo, которые математически можно представить следующим образом [6]:
|
|
(8) |
где 
-
меандровая шумоподобная помеха; 
- двухпозиционная
фазоманипулированная помеха; 
- частота меандра,
кратная 511 или 1023 кГц; Nm – коэффициент кратности меандровых импульсов; 
- расширяющий меандр, определяемый как [6]:
|
|
(9) |
Показатель Nm, приведенный в выражении (8), согласно [6] определяется следующим уравнением:
|
|
(10) |
где 
-
частота меандрового колебания; 
- частота следования
символов псевдослучайной последовательности помехи.
Используя выражение (5), и, согласно [4], комплексную огибающую спектральной плотности мощности меандровой шумоподобной помехи можно представить следующим образом:
|
|
(11) |
где 
-
спектральная плотность мощности одиночного символа меандровой псевдослучайной
последовательности (ПСП); 
- спектральная
плотность мощности меандровой ПСП.
В соответствии с [6]
величина 
может быть представлена как:
|
|
(12) |
Амплитудный спектр
меандровой ПСП является модулем функции 
:
|
|
(13) |
Спектральная плотность
мощности одиночного символа меандровой ПСП 
может
быть вычислена в соответствии с выражением [6]:
|
|
(14) |
где 
-
длительность символа меандровой ПСП.
Учитывая выражения (11), (12) и (13), получим формулу для спектра меандровой шумоподобной помехи:
|
|
(15) |
Выражение (15) позволяет оценить спектральную плотность мощности помехи с двухпозиционной фазовой манипуляцией. Тогда для помехи с многократной фазовой манипуляцией имеем:
|
|
(16) |
Оценка средней мощности МШП, согласно [5], может быть вычислена как:
|
|
Прямошумовая помеха. Прямошумовую помеху, формируемую генератором помех, можно рассматривать как стационарный белый гауссовский шум (БГШ) с ограниченным спектром и нулевым математическим ожиданием [2]:
|
|
(18) |
где 
-
математическое ожидание БГШ; 
- корреляционная
функция БГШ; 
- спектральная плотность БГШ.
Анализ эффективности подавления сигналов СРНС
В качестве критерия, определяющего воздействие преднамеренных помех на АП, примем отношение помеха-сигнал на выходе коррелятора:
|
|
(19) |
где 
- мощность
сигнала на входе АП СРНС от НКА; 
- мощность помехи на
входе АП СРНС от источника помех; 
, 
, 
-
мощность передатчика, коэффициент усиления антенны и коэффициент полезного
действия антенно-фидерного тракта НКА соответственно; 
-
количество НКА, сигналы от которых действуют на входе АП СРНС; 
- коэффициент использования мощности
передатчика; 
- спектральная плотность мощности передатчика;
- дополнительное затухание сигнала от
НКА; 
, 
и 
- мощность передатчика, коэффициент
усиления антенны и коэффициент полезного действия антенно-фидерного тракта
источника помех соответственно; 
- количество НКА,
сигналы от которых действуют на входе АП СРНС.
Выражение (19) справедливо в случае действия на входе АП СРНС структурных помех типа ПФМГ, ПФМП и МШП. Так как БГШ является некоррелированным процессом, выражение (17) для шумовой помехи можно представить как:
|
|
(20) |
где 
-
длительность кодовой посылки сигнала СРНС.
Подставив (7) в (19), получим выражение для оценки отношение помеха-сигнал при работе генератора в режиме формирования ПФМП или ПФМГ:
|
|
(21) |
где m – индекс фазовой манипуляции помехи.
Учитывая (17), отношение помеха-сигнал при работе генератора в режиме формирования МШП, определяется как:
|
|
(22) |
Результаты расчетов отношения помеха-сигнал на выходе коррелятора АП, полученные из выражений (20) – (22), приведены на рис. 1…3.
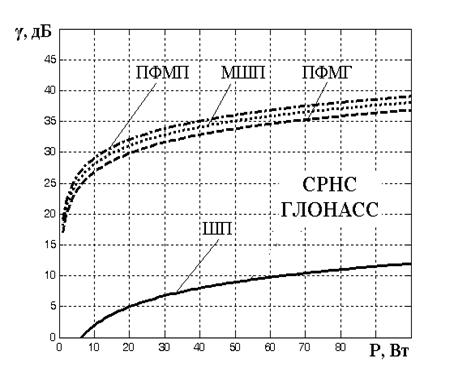
Рис.1. Отношение помеха-сигнал на
выходе коррелятора АП
при разных режимах работы генератора помех для СРНС ГЛОНАСС
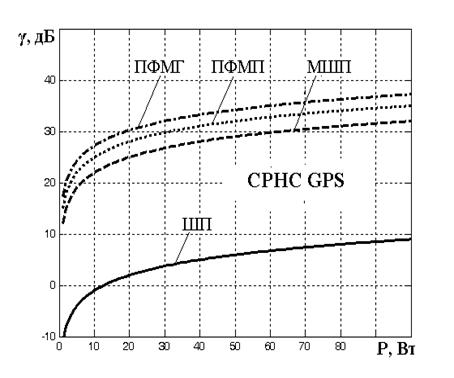
Рис.2. Отношение помеха-сигнал на
выходе коррелятора АП
при разных режимах работы генератора помех для СРНС GPS
Рис.3. Отношение помеха-сигнал на
выходе коррелятора АП
при разных режимах работы генератора помех для СРНС ГЛОНАСС
Анализ результатов и выводы
Результаты проведенных расчетов позволяют сделать следующие выводы: эффективность подавления сигналов СРНС ГЛОНАСС ПФМП превышает эффективность подавления МШП до 1,5 дБ, ПФМГ – до 2,5 дБ и прямошумовыми помехами – до 27 дБ (рис.1); эффективность подавления сигналов СРНС GPS ПФМГ превышает эффективность подавления ПФМП до 2,5 дБ, МШП – до 7 дБ и шумовыми помехами – до 28 дБ (рис.2); эффективность подавления сигналов СРНС Galileo МШП превышает эффективность подавления ПФМП до 3 дБ, ПФМГ – до 4,8 дБ и шумовыми помехами – до 30 дБ (рис.3).
Полученные результаты справедливы при подавлении сигналов одного навигационного космического аппарата (НКА). Однако, для срыва работы АП, как правило, требуется одновременное подавление сигналов от нескольких НКА. Частотное разделение каналов, используемое в СРНС ГЛОНАСС, с энергетической точки зрения делает ее более помехоустойчивой по сравнению с СРНС GPS и СРНС Galileo, в которых применяется кодовое разделение сигналов.
Литература
1. Куприянов А.И., Сахаров А.В. Теоретические основы радиоэлектронной борьбы. Учебное пособие. М.: Вузовская книга, 2007. – 356 с
2. Шебшаевич В.С., Дмитриев П.П. и др. Сетевые спутниковые радионавигационные системы. М.: Радио и связь. – 1993. – 408 с.
3. Конин В.В., Конина Л.А. Спутниковые системы навигации. Учебное пособие. Киев – 2008. – 286 с.
4. ГЛОНАСС. Принципы построения и функционирования/ Под ред. А.И. Перова, В.Н. Харисова. Изд. 3-е, перераб. – М.: Радиотехника – 2005. – 688 с.
5. Варакин Л.Е. Системы связи с шумоподобными сигналами. – М.: Радио и связь. – 1985. – 344 с.
6. Ярлыков М.С. Меандровые шумоподобные сигналы (ВОС-сигналы) в новых спутниковых радионавигационных системах // Радиотехника. – 2007. – с. 3-12.