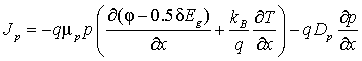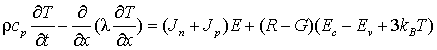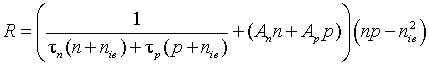УДК 621.382

МОДЕЛИРОВАНИЕ ТЕПЛОВОГО ПОРАЖЕНИЯ ДИОДНЫХ ПОЛУПРОВОДНИКОВЫХ СТРУКТУР
ПОЛИИМПУЛЬСНЫМ СВЕРХВЫСОКОЧАСТОТНЫМ РАДИОИЗЛУЧЕНИЕМ

 

С. А. Мещеряков

Федеральное автономное учреждение "Государственный научно-исследовательский
испытательный институт проблем технической защиты информации ФСТЭК России"

 

Получена 2 апреля 2013 г., после доработки - 3 июля 2013г.

 

Аннотация. В рамках численной модели в диффузионно-дрейфовом тепловом приближении приведены результаты моделирования энергомощностных и температурных характеристик для диодных биполярной структуры и структуры с барьером Шоттки на основе кремния при воздействии последовательности импульсов сверхвысокочастотного (СВЧ) электромагнитного излучения. Показана определяющая роль тепловой релаксации в поведении энергетических характеристик полупроводниковых структур при тепловом поражении полиимпульсным СВЧ-воздействием. Определены характерные области частотных зависимостей полученных энергомощностных характеристик.

Ключевые слова: численная модель, диодная структура, СВЧ-импульс, полиимпульсный режим, тепловое поражение.

Abstract: Within the limits of numerical model in drift-diffusion thermal approach results of microwaves multipulse mode thermal failure power and temperature characteristics simulation for silicon diode bipolar and Schottky-barrier structures are presents. Determinative function of thermal relaxation in behavior of energy semiconductor structures characteristics by multipulse microwave action thermal failure is demonstrated. Characteristic regions of power characteristic frequency dependences are determinate.

Key words: numerical model, diode structure, microwave pulse, multipulse mode, thermal failure.

 

Введение

Исследованию влияния мощного сверхвысокочастотного (СВЧ) импульсного электромагнитного излучения (ЭМИ) посвящен ряд работ в отечественной и зарубежной литературе. Среди них следует отметить работы [1–3], позволившие дать описания энергомощностных характеристик теплового поражения полупроводниковых структур однократным импульсом ЭМИ в рамках решения аналитического уравнения теплопроводности и статистическую модель накопления повреждений [4, 5] полиимпульсного воздействия.

Указанные модели используют ряд определенных допущений и предположений. Во-первых, воздействующая энергия импульса ЭМИ рассматривается исключительно как тепловая энергия, эквивалентно замещающая реальные процессы саморазогрева, связанного с протекающим внутри структуры электрическим током. Это позволяет решать только уравнение теплопроводности без расчета "электрической" составляющей. Во-вторых, в большинстве случаев считается, что эта энергия изменяет температурное состояние достаточно ограниченной обедненной области структуры, поведение которой определяет характеристики структуры в рабочем режиме. В-третьих, тепловая релаксация данной области к исходной температуре (температуре окружающей среды) по окончании импульсного воздействия считается достаточно быстрой, и при полиимпульсном воздействии с малой частотой следования импульсов накопления тепла не происходит [4,5]. Между тем, при импульсных воздействиях, существенно превышающих параметры рабочих сигналов, в структуре начинают сказываться физические эффекты, связанные с высоким уровнем инжекции носителей заряда. В данном режиме указанные допущения уже не являются справедливыми, а на механизмы токопереноса и, соответственно, рассеивания электрической мощности, начинают влиять остальные области структуры (подложка, квазинейтральные области и т.д.) [6,7]. Это требует совместного рассмотрения электрической и тепловой составляющей процесса воздействия наведенного на структуру импульсами ЭМИ сигнала с учетом ее реальной конструкции, электро- и теплофизических характеристик полупроводникового материала и теплоотводящих характеристик контактно-металлизационных систем.

Цель настоящей работы – в рамках численной модели в диффузионно-дрейфовом тепловом приближении (ДДМТ) продемонстрировать поведение энергомощностных характеристик диодных биполярной (p – n-переходной) структуры и униполярной структуры с барьером Шоттки в условиях мощного полиимпульсного СВЧ-воздействия на основе решения полной электротепловой задачи.

 

Математическая модель

Для описания кремниевой диодной структуры в динамическом режиме полиимпульсного воздействия воспользуемся системой уравнений одномерной ДДМТ, содержащей уравнение полного тока, два уравнения непрерывности для электронов и дырок, дополненные уравнениями переноса тока, и уравнение теплопроводности, позволяющее учитывать разогрев структуры в процессе протекания тока:

                                                                (1)

                                    (2)

                                     (3)

                      (4)

где φ – электрический потенциал, e₀ – диэлектрическая постоянная, e – диэлектрическая постоянная полупроводника, n, p – концентрация электронов и дырок, q – заряд электрона, J_n, J_p – плотность тока электронов и дырок, G – темп генерации, R – темп рекомбинации, m_n, m_p – подвижность электронов и дырок, dE_g – сужение ширины запрещенной зоны в зависимости от степени легирования, D_n, D_p – коэффициенты диффузии электронов и дырок, E_c, E_v – энергетические уровни дна зоны проводимости и потолка валентной зоны полупроводника, r – плотность вещества, c_p – удельная теплоемкость вещества, l –коэффициент теплопроводности вещества, T – абсолютная температура, k_B – постоянная Больцмана.

Темп генерации G, входящий в уравнения системы (1) и уравнение (4), с учетом процессов ударной ионизации и туннелирования может быть представлен как

                                      (5)

где α_n, α_p – коэффициенты ударной ионизации электронов и дырок, A, B – эмпирические коэффициенты туннельной генерации.

Общий темп рекомбинации, включающий рекомбинацию Шокли-Рида-Холла и рекомбинацию Оже представляется уравнением

                      (6)

где τ_n, τ_p – времена жизни электронов и дырок; n_ie – собственная концентрация примеси в полупроводнике с учетом эффектов сильного легирования и сужения запрещенной зоны; A_n, A_p – коэффициенты Оже-рекомбинации электронов и дырок.

Согласно уравнению (4), рассеиваемая внутри диодной структуры электрическая мощность преобразуется в Джоулево тепло и термостимулированные генерационно-рекомбинационные процессы. Это приводит к изменению объемной температуры, и, следовательно, через изменение электрофизических параметров материала к изменению электрического режима, а через измененную электрическую рассеиваемую мощность к новому изменению температуры (тепловая обратная связь).

Интегрирование по длине моделируемой структуры правой части уравнения (4) дает мгновенную рассеиваемую плотность мощности P. Плотность энергии W, рассеиваемой за время полиимпульсного воздействия t_пи, вычисляется из выражения (7), а средняя плотность мощности P_ср за время полиимпульсного воздействия – из выражения (8)

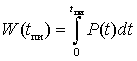,                                                                               (7)

.                                                                    (8)

Система (1) – (4) содержит нелинейные дифференциальные уравнения в частных производных, разрешимые в общем случае только численными методами. Начальным условием для динамической задачи являются статические распределения j(x), n(x), p(x) и T(x) при нулевом постоянном смещении.  Граничные условия для электрического потенциала j на омических контактах полупроводниковых структур в каждый момент времени воздействия импульса определяются приложенным напряжением СВЧ-сигнала u(t) и равны нулю в его отсутствии (с учетом контактной разности потенциалов). Граничные условия для концентраций носителей на омических контактах берутся термодинамически равновесными. Тепловой поток на теплоизолированном контакте приравнивается к нулю (). Температура на теплоотводящем контакте принимается равной температуре окружающей среды (T₀ = 20 ºС) в случае коэффициента теплопереноса h = ¥ или определяется согласно выражению в случае его конечной величины.

 

Результаты моделирования

Вычисления будем проводить для p – n-переходной структуры и структуры с барьером Шоттки на основе кремния. Электрофизические параметры кремния (подвижности свободных носителей заряда, теплопроводность и др.) и их зависимости от температуры взяты в соответствии с [8].

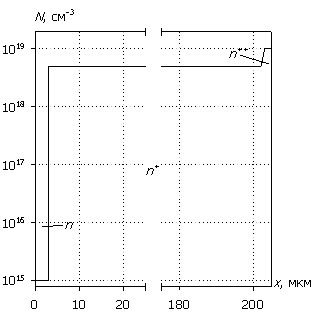
На рис. 1а представлен профиль распределения легирующей примеси N(x) в биполярной  n⁺ – p – p⁺ – p⁺⁺-диодной структуре. Он состоит из четырех областей: эмиттера с глубиной залегания перехода 1 мкм и уровнем донорного легирования N_d+ = 10¹⁹ см^-3 (в максимуме); базовой области (низколегированной эпитаксиальной пленки) с толщиной w_p = 3 мкм и уровнем акцепторного легирования N_a = 10¹⁵ см^-3; высоколегированной акцепторами монокристаллической подложки с толщиной w_p+ = 200 мкм и уровнем легирования N_a+ = 5×10¹⁸ см^-3 и области приконтактного акцепторного легирования с толщиной w_p++ = 2 мкм и уровнем  N_a++ = 10¹⁹ см^-3. К эмиттеру примыкает теплоизолированный омический контакт, с другой стороны структуры – омический теплоотводящий контакт.

На рис. 1б представлен профиль распределения легирующей примеси N(x) в диодной n – n⁺ – n⁺⁺-структуре с барьером Шоттки. Он состоит из трех областей: низколегированной эпитаксиальной пленки с толщиной w_n = 3 мкм и уровнем донорного легирования N_d = 10¹⁵ см^-3, высоколегированной монокристаллической подложки с толщиной w_n+ = 200 мкм и уровнем донорного легирования N_d+ = 5×10¹⁸ см^-3 и области приконтактного легирования с толщиной w_n++ = 2 мкм и уровнем донорного легирования N_d++ = 10¹⁹ см^-3. К эпитаксиальной пленке примыкает теплоизолированный выпрямляющий контакт Шоттки с высотой потенциального барьера F_b = 0.75 эВ, с другой стороны структуры – омический теплоотводящий контакт. Приведенные параметры соответствуют промышленно выпускаемым диодным структурам для СВЧ электроники.

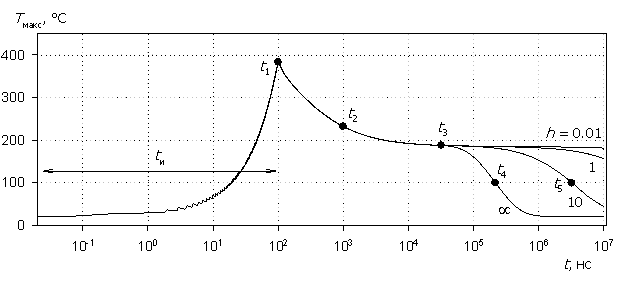
На рис. 2 представлены результаты моделирования в рамках ДДМТ процессов нагревания при воздействии и тепловой релаксации после воздействия однократного СВЧ-импульса с несущей частотой f_и = 1 ГГц, амплитудой U₀ = 200 В и длительностью t_и = 100 нс. Максимальная температура T_макс приходится на теплоизолированный эмиттерный контакт.

 

  

(а)                                                            (б)

Рис. 1. Профили легирующей примеси диодных структур: (а) – биполярная структура, (б) – структура с барьером Шоттки.

 

Рис. 2. Нагревание и тепловая релаксация температуры в биполярной
n⁺ – p – p⁺ – p⁺⁺-структуре.

 

Из графиков на рис. 2 следует, что процесс термического саморазогрева структуры за весьма короткое время действия однократного СВЧ-импульса не зависит от значения коэффициента теплопереноса h теплоотводящего омического контакта. Процесс тепловой релаксации температуры к исходному состоянию, напротив, имеет существенную зависимость от h для значений t > 30 мкс. На представленных графиках можно выделить три области тепловой релаксации. Первая область соответствует достаточно быстрому снижению температуры с 400 °С до 200 °С во временном интервале 100 нс…5 мкс. Далее следует область некоторой стабилизации температуры во временном интервале, длительность которого существенно зависит от значения h. В частности для h = ¥ правая граница интервала соответствует t = 30 мкс, для h = 0.01 Вт/(°С×см2) – t = 7 мс. Далее снова следует область снижения максимальной температуры до температуры окружающей среды, длительность которой также находится в зависимости от значения h.

На рис. 3 представлены внутренние распределения температуры по длине моделируемой структуры, соответствующие отмеченным на рис. 2 временным точкам t₁ – t₅.

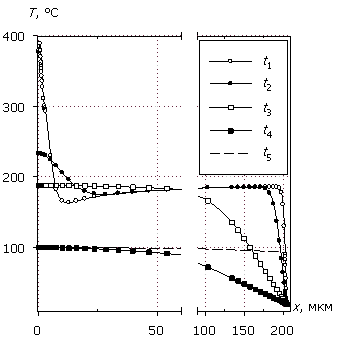
Рис. 3. Распределения T(x) в различные моменты времени процесса
тепловой релаксации.

 

Приведенные пространственные распределения температуры детализируют особенности временных диаграмм рис. 2. В момент окончания импульсного воздействия t₁ наблюдается резкая неравномерность распределения температурного поля. Вблизи теплоизолированного контакта в активной рабочей области полупроводниковой структуры (порядка 10 мкм) локализованная при воздействии импульса электрическая мощность создает двукратно превышающую по сравнению с остальным объемом температуру. Тепловая релаксация начинается с выравнивания температурного распределения по длине структуры за счет взаимно уравновешивающих друг друга процессов. С одной стороны, за счет механизмов теплопроводности мы получаем диффузию тепла от теплоизолированного контакта к теплоотводящему контакту, с другой стороны – отвод тепла от теплопроводящего контакта (рис. 3, момент времени t₂). Этот процесс дополнительно поддерживается тепловыми составляющими токов проводимости (см. уравнения (2), (3)), и рекомбинационными процессами существенной концентрации избыточных электронов и дырок, накопленных в низколегированной области полупроводниковой структуры за время действия мощного СВЧ-импульса. При этом следует отметить низкую теплопроводность наиболее разогретых областей [8], что также вносит вклад в замедление релаксационного процесса.

После выравнивания температурного поля в большей части структуры процесс теплоотвода начинает превалировать и структура начинает остывать со стороны теплоотводящего контакта с общим снижением температуры по всей длине (рис. 3, моменты времени t₃, t₄). Именно в этом временном интервале важную роль начинают играть теплоотводящие характеристики обратного контакта, и чем меньше коэффициент h, тем более ровное распределение температурного поля мы будем наблюдать (рис. 3, момент времени t₅).

Так как для теплоотводящих систем полупроводниковых электронных компонентов h не превышает значения 1 Вт/(°С×см²) [9,10], становится очевидным факт – накопление тепла и рост температуры в структуре от импульса к импульсу при мощном полиимпульсном СВЧ-воздействии возможен даже при частотах следования импульсов в единицы и десятки герц, что опровергает исходное предположение статистической модели [4,5] о быстром восстановлении температуры. В зависимости от того, на какую область тепловой релаксации будет приходиться очередной импульс СВЧ-воздействия (другими словами, какая частота их следования) будут наблюдаться различные участки поведения энергетических характеристик разогрева.

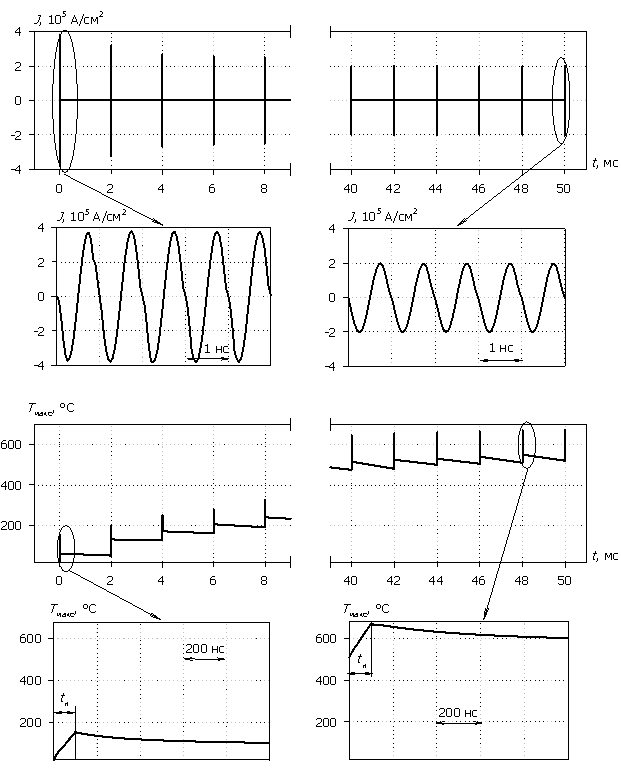
На рис. 4 представлены временные зависимости плотности тока J и максимальной температуры T_макс в диодной биполярной структуре при мощном полиимпульсном СВЧ-воздействии с частотой следования импульсов f = 500 Гц, демонстрирующие динамику теплового саморазогрева до максимальной температуры 675 °С (температура плавления алюминиевой металлизации). На врезках в увеличенном масштабе показаны начало и конец полиимпульсного воздействия. Из представленных данных видно, что при столь мощном воздействии диодная структура пропускает ток в обоих направлениях и с каждым последующим импульсом плотность его несколько снижается, стабилизируясь на некотором уровне к окончанию воздействия. Аналогичное поведение демонстрируют экспериментальные данные для точечного смесительного СВЧ диода Д405, полученные в [5]. Причиной подобного поведения является снижение величин подвижности и коэффициентов диффузии свободных носителей, входящих в уравнения переноса тока (2) и (3) при увеличении температуры, в результате чего падает общая проводимость структуры. Дополнительно к этому снижается коэффициент теплопроводности в областях максимального разогрева, что ухудшает теплоотвод из этих областей.

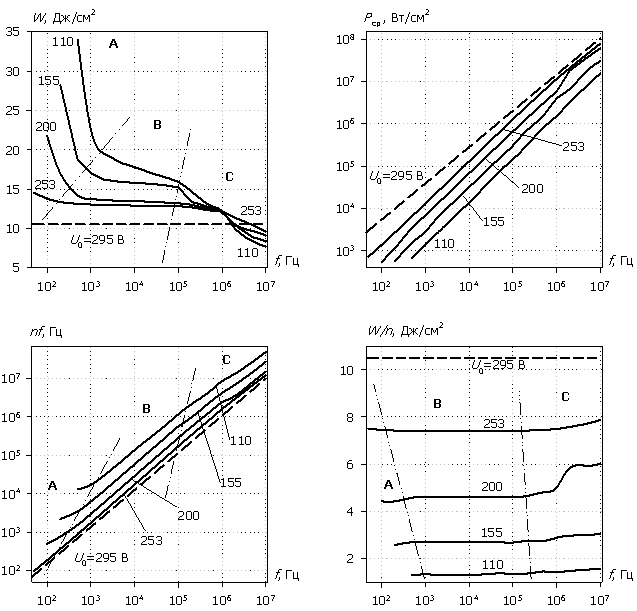
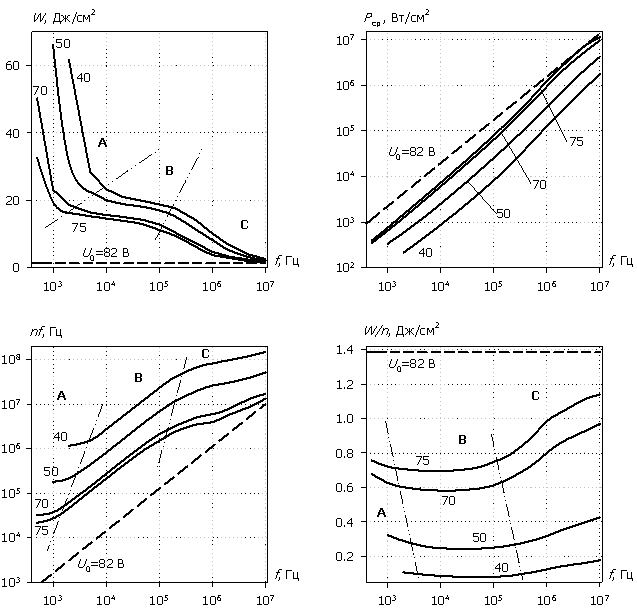
На рис. 5, 6 приведены рассчитанные в рамках ДДМТ энергомощностные характеристики диодных структур – биполярной и униполярной с барьером Шоттки – в зависимости от частоты следования импульсов и амплитуды напряжения воздействующего сигнала. Пунктирными линиями на графиках показаны характеристики однократного СВЧ-импульса, приводящие к одинаковому с полиимпульсным воздействием разогреву до T_макс = 675 °С. Согласно графикам для обоих типов структур частотные зависимости энергомощностных характеристик имеют три характерные области.

 

Рис. 4. Временные зависимости J(t) и T_макс(t), биполярная структура, U₀ = 110 В, f_и = 1 ГГц, t_и = 100 нс,  f = 500 Гц.

 

 Область А соответствует относительно низким частотам следования импульса, не превышающим 5 кГц. Для этой области свойственны асимптотический рост плотности энергии W, необходимой для разогрева структуры до определенной температуры, и насыщение характеристики n´f (f) (произведение количества импульсов на их частоту повторения). В пределе мы имеем для данной области некоторую минимальную частоту  f_мин, выше которой саморазогрев еще возможен, и определяемую условием n´f = const. Физически это соответствует

 

Рис. 5. Энергомощностные характеристики биполярной структуры.

 

Рис. 6. Энергомощностные характеристики структуры с барьером Шоттки.

 

ситуации, когда между импульсами структура успевает практически полностью остывать (по расчетам до 40…50 °С), при этом чем выше амплитуда воздействующего сигнала, тем меньше значение f_мин. Асимптотическое поведение энергии в области А, связанное с f_мин, позволяет говорить о некотором пороговом "частотном скачке" при фиксированной мощности воздействия. В частности, на рис. 5 при U₀ = 200 В и f = 100 Гц достигается T_макс = 675 °С, но уже при f = 50 Гц достигнуть данную температуру не удалось при весьма длительных моделируемых временах воздействия.

Указанная f_мин для униполярной структурой с барьером Шоттки имеет в сравнении с биполярной структурой большее значение (рис. 6) в силу лучших частотных свойств барьеров Шоттки, связанных с меньшей концентрацией неосновных носителей заряда и малым временем их рассасывания. Это приводит к меньшей зависимости тока (а через тепловую обратную связь и саморазогрева) от эффектов их инжекции и экстракции.

Область B приблизительно соответствует диапазону частот следования импульсов 10 … 100 кГц. Для этой области характерны достаточно слабые зависимости от частоты плотности энергии W и количества импульсов n. При увеличении амплитудного значения U₀ воздействующего импульса энергия, необходимая для разогрева структуры до определенной температуры, стремится к постоянному значению, а число импульсов соответствует условию n » const >1. Физически это соответствует ситуации, когда, в общем, неравномерное температурное распределение, сформированное за время действия импульса, выравнивается в интервалы отсутствия воздействия. Часть тепла при этом успевает отводиться, но от импульса к импульсу мы имеем достаточно существенное его накопление.

Область C соответствует диапазону частот следования импульсов от 100 кГц до f = 1/t_и (в нашем случае 10 МГц). Особенностью данной области является стремление параметров энергомощностных зависимостей к характеристикам одиночного воздействия. С ростом частоты количество импульсов n, требуемое для разогрева структуры падает, а характеристика n´f изменяет наклон в сравнении с областью B, что наиболее выражено для униполярной структуры с барьером Шоттки. В данной ситуации мы имеем во время воздействия СВЧ-импульса локальный разогрев части структуры (как правило, со стороны теплоизолированного контакта), сформированное при этом температурное поле в интервалы отсутствия воздействия не успевает выравниваться по структуре, а накопленное тепло практически не отводится. В работах [2,3] для однократного импульсного воздействия такой режим определяется как  адиабатический.

Отметим еще одну особенность области C. Как следует из рис. 5, 6 в диапазоне 1…10 МГц для биполярной структуры полиимпульсные зависимости W(f) имеют точки пересечения с моноимпульсной характеристикой, стремясь к ней при увеличении U₀ и больших частотах "снизу". Униполярные структуры с барьером Шоттки таких точек не имеют и их полиимпульсные зависимости стремятся к моноимпульсной характеристике исключительно "сверху". Причина этому в следующем. Рекомбинационные процессы в биполярных структурах более существенны, чем в структурах с барьером Шоттки, и согласно уравнению (4) вклад в тепловые процессы рекомбинации как источника тепла более значим. Это позволяет достаточно эффективно компенсировать приемник тепла, связанный с генерацией свободных носителей заряда, однако с увеличением амплитуды воздействующего импульса (или ростом мощности воздействия) степень компенсации уменьшается (темп генерации растет быстрее темпа рекомбинации). Генерационными эффектами объясняется и рост в указанном диапазоне частот зависимости W/n (плотности энергии, приходящейся на один импульс).

 

Заключение

Приведенные результаты моделирования мощного полиимпульсного СВЧ-воздействия на диодные полупроводниковые структуры в рамках ДДМТ показывают, что основным физическим процессом их поражения следует считать накопление тепловой энергии от импульса к импульсу и термический разогрев различных областей структуры. При этом термин "тепловое поражение" может быть рассмотрен, в общем случае, несколько шире, чем катастрофический отказ, связанный с выгоранием. К нему можно также отнести и функциональный сбой (с температурой саморазогрева 200…350 °С) при относительно невысоких уровнях полиимпульсного воздействия, который потенциально возможен даже при частотах следования импульсов в единицы и десятки Гц и будет иметь аналогичные представленным в этой работе тенденции поведения.

Характер электрических и энергомощностных зависимостей для диодных структур в условиях полиимпульсного воздействия, модельно полученных в рамках ДДМТ, соответствует известным экспериментальным данным. К ним можно отнести снижение и последующую стабилизацию токового отклика диодной структуры при полиимпульсном воздействии [5] и меньшие уровни энергетического воздействия, приходящиеся на один импульс, в сравнении с тепловым поражением однократным импульсом [5,11]. При этом следует заметить, что общая затрачиваемая энергия полиимпульсного воздействия на разогрев структуры до определенной температуры в большинстве случаев выше, чем энергия моноимпульсного воздействия.

Причинами статистической флуктуации энергомощностных характеристик [5], полученных экспериментальным путем, по всей видимости, следует считать известные в микроэлектронике факты – локализацию тока в достаточно ограниченных областях полупроводниковых структур ("шнурование") и флуктуации характеристик теплоотвода.

 

Литература

1.            Wunsh D., Bell R. Determination of threshold failure levels of semiconductor diodes and transistors due to pulse voltage // IEEE Trans. 1968. V. NS-15. P.244–259.

2.            Taska D.M. Pulse power failure modes in semiconductors // IEEE Trans. 1970. V. NS-17. P.364.

3.            Dwyer V.M., Franklin A.J., Campbell D.S. Thermal failure in semiconductor devices// Solid-State Electron. 1990. V.33. P.553–560.

4.          А.В. Ключник, А.В. Солодов  Статистическая модель повреждения цифровых интегральных схем импульсным радиоизлучением // Радиотехника. 2010. № 2. С. 37–42.

5.            А.В. Ключник, Ю.А. Пирогов, А.В. Солодов Статистика повреждения СВЧ диодов импульсным радиоизлучением // Журнал радиоэлектроники: электронный журнал. 2010. № 12. URL: http://jre.cplire.ru/jre/dec10/1/text.pdf

6.            С.А. Мещеряков, А.И. Прокопьев  Влияние барьерных свойств низкоомной подложки на модуляцию сопротивления базы диода Шоттки // Изв. вузов. Электроника. 1998. № 2. С. 27–29.

7.          Prokopyev A.I., Mesheryakov S.A.  Static characteristics of high-barrier Schottky diode under high level injection // Solid-St. Electron. 1999. V 43.  N 9. P. 1747–1753.

8.            NSM Archive – Physical Properties of Semiconductors // [Электронный ресурс]. URL: http://www.ioffe.rssi.ru\SVA\NSM\Semicond\index.html

9.            Дульнев Г.Н. Теплообмен в радиоэлектронных устройствах – М.-Л.: Госэнергоиздат, 1963. – 288 с.

10.       Тугов Н.М. и др. Полупроводниковые приборы – М.: Энергоатомиздат, 1990. – 576 с.

11.      Юшков Ю.Г., Чумерин П.Ю., Артеменко С.Н. и др. Экспериментальное исследование воздействия сверхвысокочастотных импульсов на работу персонального компьютера // Радиотехника и электроника. 2001. Т. 46. №8. С. 1020–1024.