УДК 538.566.2:621.372.8
Возбуждение линии поверхностной волны электрическим дипольным источником
Г. Г. Грачев, В. В. Шевченко
Институт радиотехники и электроники им. В.А.Котельникова РАН
Статья получена 4 июля 2014 г.
Аннотация. Приводятся результаты решения задачи о возбуждении паразитной поверхностной волны в направляющей линии типа Губо-Хармса внешним дипольным источником.
Ключевые слова: поверхностные волны, линии поверхностной волны, ЛПВ для телевидения.
Abstract. The problem solution results of parasitic surface wave excitation in the surface wave Goubau-Harms line by an external dipole source are presented.
Key words: surface waves, surface wave lines, SWL for the television.
При передаче информации, в частности телевидения, по линии поверхностной волны (ЛПВ), открытой волноведущей структуре, возникают помехи из-за возбуждения в ней паразитной волны внешними источниками. Для оценки величины мощности такой волны в данной работе приводятся результаты решения задачи о возбуждении поверхностной волны дипольным источником. Использовалась модель ЛПВ типа Губо-Хармса в виде импедансного провода, то есть провода с конечным поверхностным импедансом.
Из работы [1] следует, что задача о возбуждении волн, направляемых открытыми волноводами, в частности поверхностных волн, составляющих дискретную часть полного спектра волн открытого волновода, может быть решена тем же векторным методом, который был развит для волн закрытых полых волноводов. Поэтому полученные для таких волноводов результаты [2] были использованы при решении векторной задачи о возбуждении поверхностной волны, распространяющейся вдоль импедансного провода, дипольным источником.
Отличные от нуля компоненты поля
гармонической по времени с частотой ![]() поверхностной волны на
круглом импедансном проводе имеют вид [1-3]
поверхностной волны на
круглом импедансном проводе имеют вид [1-3]
 (1)
(1)
где опущена зависимость от времени exp(iωt); ![]() ,
,![]() , z – поперечные и продольная цилиндрические координаты,
, z – поперечные и продольная цилиндрические координаты, ![]() ,
, ![]() - длина
волны в свободном пространстве (с параметрами
- длина
волны в свободном пространстве (с параметрами ![]() ,
,![]() ),
), ![]() [Ом]
– волновое сопротивление свободного пространства,
[Ом]
– волновое сопротивление свободного пространства,
![]() =(1+p2)1/2
(2)
=(1+p2)1/2
(2)
- коэффициент замедления поверхностной волны, p – решение дисперсионного уравнения
![]() ,
Zs – индуктивный поверхностный импеданс
провода,
,
Zs – индуктивный поверхностный импеданс
провода, ![]() - радиус провода,
- радиус провода, ![]() ,
,
![]() - цилиндрические функции Макдональда.
- цилиндрические функции Макдональда.
На основании [1,2] амплитуда А
поверхностной волны, возбуждаемой током J
электрического диполя малой длины ![]() , была получена в
виде
, была получена в
виде
где ![]() - угол между осью
провода и направлением проекции оси диполя на координатную плоскость
- угол между осью
провода и направлением проекции оси диполя на координатную плоскость ![]() ,z;
,z; ![]() ,
, ![]() -
компоненты электрического поля поверхностной волны (1) при А=1,
-
компоненты электрического поля поверхностной волны (1) при А=1, ![]() - координаты расположения центра
дипольного источника,
- координаты расположения центра
дипольного источника,
Мощность, переносимая поверхностной волной в одну из сторон (вдоль оси z и в противоположном направлении) равна
Приложения
1. Поверхностные импедансы [3-5]
Поверхностный импеданс линии Зоммерфельда – немагнитного металлического провода –
![]() ,
(7)
,
(7)
где ![]() – толщина скин-слоя:
– толщина скин-слоя:
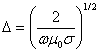 ,
(8)
,
(8)
![]() – удельная
проводимость металла.
– удельная
проводимость металла.
Для меди и алюминия [3]
где f –
частота поля в Гц. При f в МГц величина ![]() получается в мкм (вместо мм).
получается в мкм (вместо мм).
Поверхностный импеданс линии Губо-Хармса,
т.е. металлического провода покрытого слоем диэлектрика с относительной диэлектрической
проницаемостью ![]() , равен
, равен
 (10)
(10)
при ka<<1. Здесь не учитываются диэлектрические потери мощности поля и потери из-за проводимости в проводе (p –вещественно), которые рассчитываются отдельно и приводятся ниже.
2. Решение дисперсионного уравнения (3) при pka<<1 для ЛПВ Губо-Хармса рекуррентным методом
Здесь и ниже используются приближения:
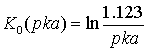 ,
, 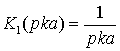 ,
, 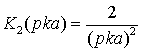 . (11)
. (11)
На основании (3), (11) получаем
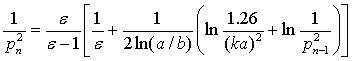 ,
(12)
,
(12)
где n=1,2,3… шаги итерации,
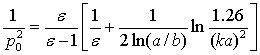 . (13)
. (13)
Расчет ведется до стабилизации pn с точностью до трех значащих цифр.
3. Коэффициент передачи мощности от источника к поверхностной волне
На основании (5), (6), (11) для коэффициента передачи мощности от диполей, оси которых ориентированы соответственно параллельно и ортогонально к оси провода, имеем
![]() ,
, 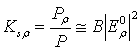 , (14)
, (14)
где Р – полная мощность, излучаемая диполем,
приближенно равная мощности излучения в свободное пространство ![]() ,
,
 , (15)
, (15)
![]() ,
, ![]() . (16)
. (16)
4. Потери энергии при распространении поверхностной волны вдоль ЛПВ Губо-Хармса
Потери в диэлектрической оболочке [3,4]
 , (17)
, (17)
где ![]() - потери мощности в
диэлектрике на единицу длины линии (1 м),
- потери мощности в
диэлектрике на единицу длины линии (1 м), ![]() -
полный поток мощности, переносимый волной,
-
полный поток мощности, переносимый волной, ![]() -
тангенс угла потерь,
-
тангенс угла потерь,
 . (18)
. (18)
Потери в немагнитной металлической сердцевине линии [3,4]
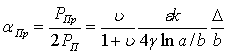 , (19)
, (19)
где Δ – толщина скин-слоя (9).
Полные потери ![]() в
децибелах равны
в
децибелах равны
![]() [Дб/м].
[Дб/м].
5. Численные результаты
На Рис. 1 представлено поперечное сечение
ЛПВ Губо-Хармса.
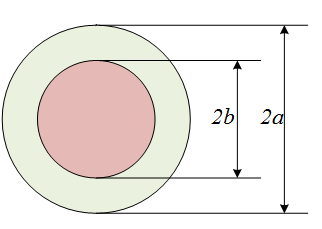
Рис. 1. Сечение ЛПВ Губо-Хармса – цилиндрической однопроводной металлической линии, покрытой слоем диэлектрика.
Численные результаты, полученные для коэффициентов
передачи мощности трех видов указанной линии с параметрами ![]() =2,25 (эквивалентная оценочная величина
между 2 и 2,5, соответствующая полиэтилену),
=2,25 (эквивалентная оценочная величина
между 2 и 2,5, соответствующая полиэтилену), ![]() (TV стандарт, применяемый в ФРГ [4]) по
приведенным выше формулам, даны на рис.2-4.
(TV стандарт, применяемый в ФРГ [4]) по
приведенным выше формулам, даны на рис.2-4.
a=0,2см, b=0,085см
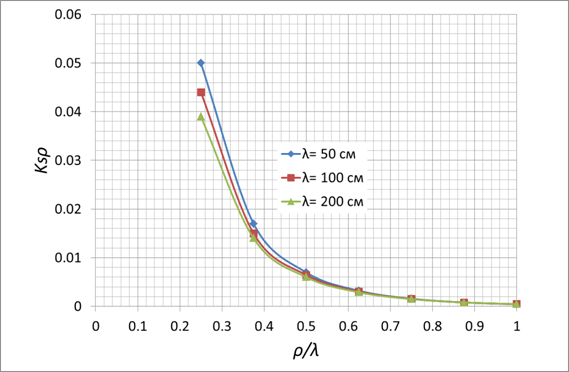

Рис. 2.
a=0,5см, b=0,2см
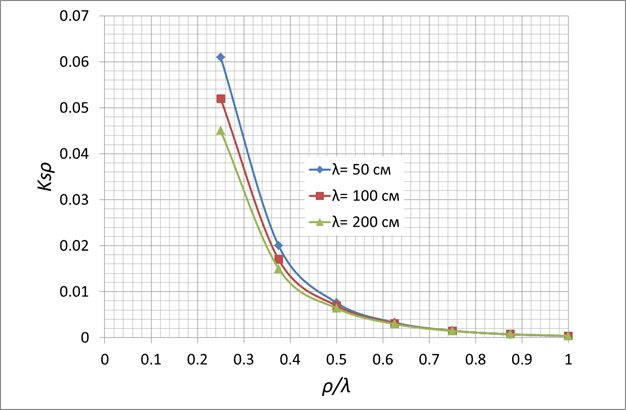
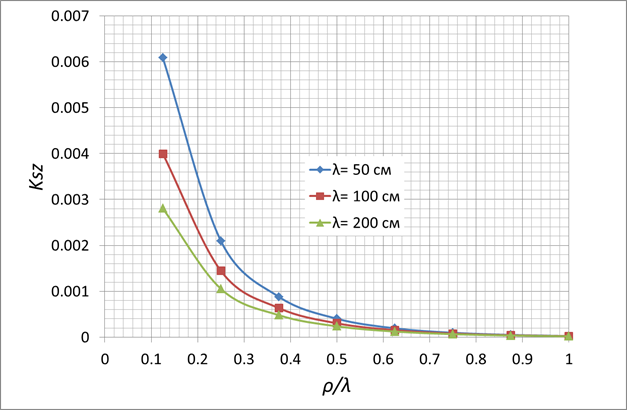
Рис. 3.
a=0,9см, b=0,6см
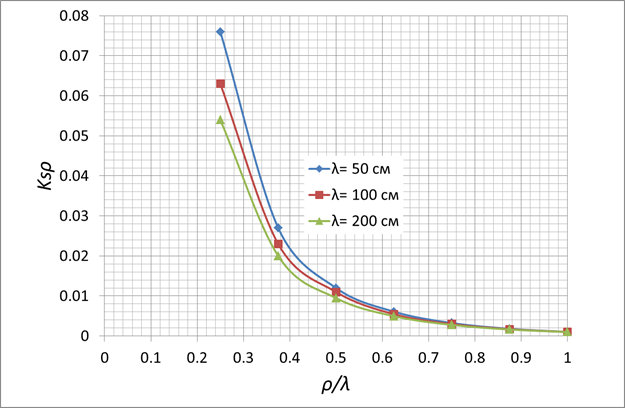
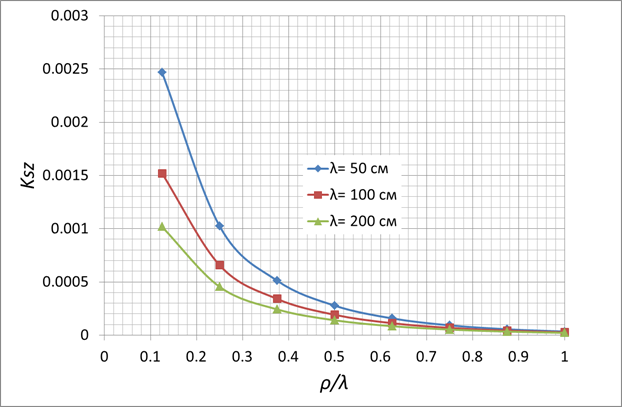
Рис. 4.
Аналогичные результаты, полученные методом
вычислительного эксперимента, даны на рис. 5-7, а на рис. 8-10 представлены графики
сравнения этих результатов. Заметим, что на всех представленных графиках по
горизонтальной оси под ![]() понимается координата
расположения центра дипольного источника, ранее обозначенная в объяснении
формулы (4) через
понимается координата
расположения центра дипольного источника, ранее обозначенная в объяснении
формулы (4) через ![]()
Некоторое расхождение кривых в рамках одного
и того же порядка величины на графиках сравнения связано с тем, что формулы
были выведены для возбуждения поверхностной волны диполями малых размеров (l<<![]() ),
а вычислительный эксперимент был выполнен для резонансных диполей (l=
),
а вычислительный эксперимент был выполнен для резонансных диполей (l=![]() /2).
/2).
На рис. 11-15 представлены результаты
расчетов частотных зависимостей потерь энергии при распространении
поверхностной волны для линий Губо-Хармса с медной и алюминиевой жилами по приведенным
формулам и, для сравнения, полученные методом вычислительного эксперимента для ![]() =2,25,
=2,25, ![]() .
.
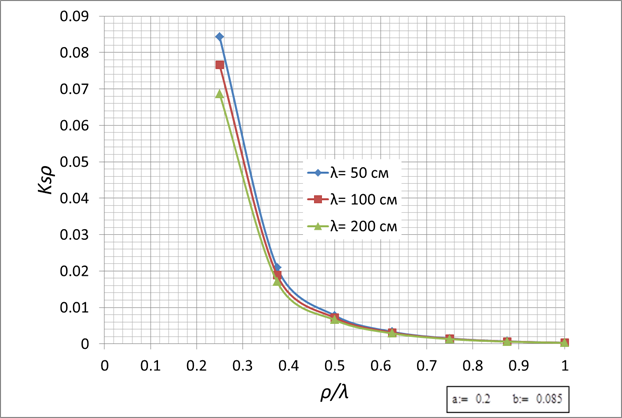
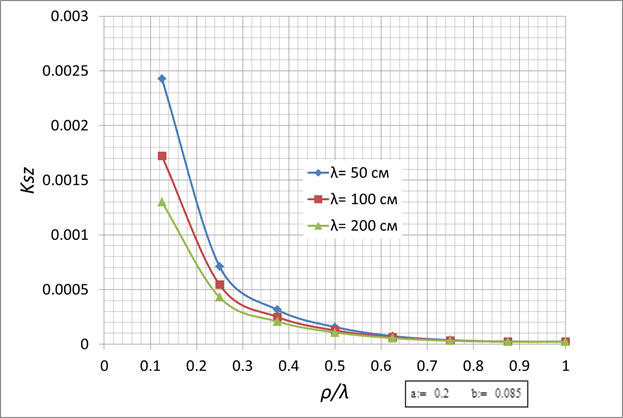
Рис. 5.
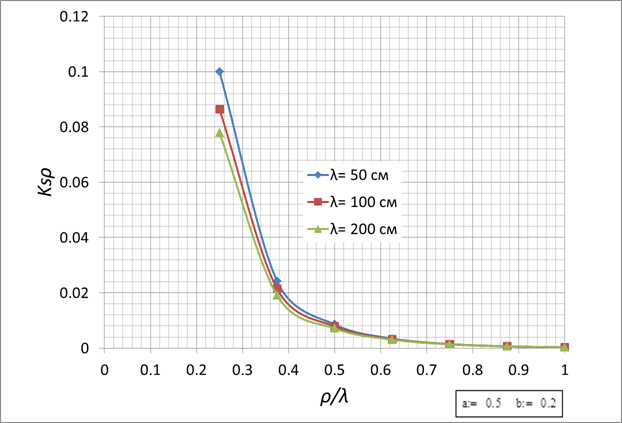
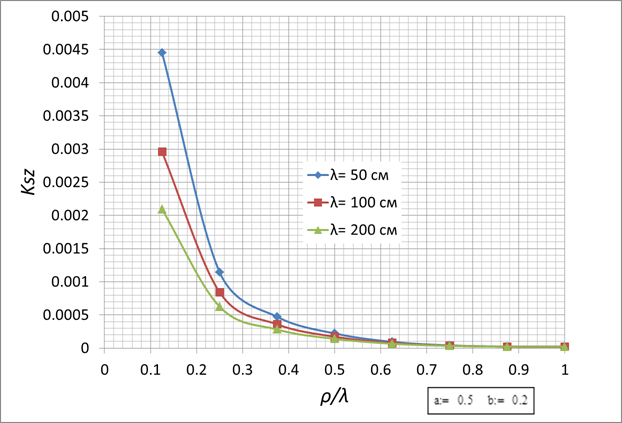
Рис. 6.
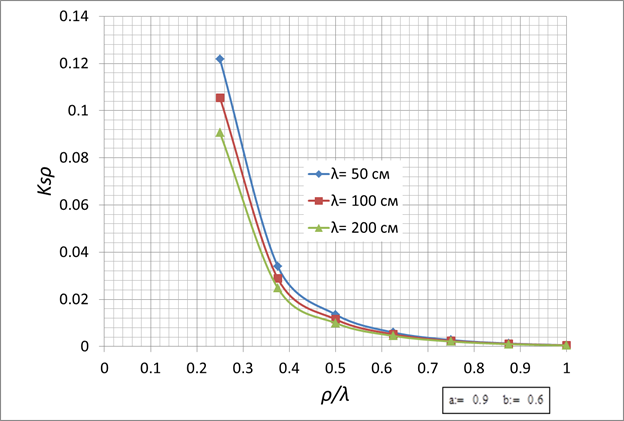
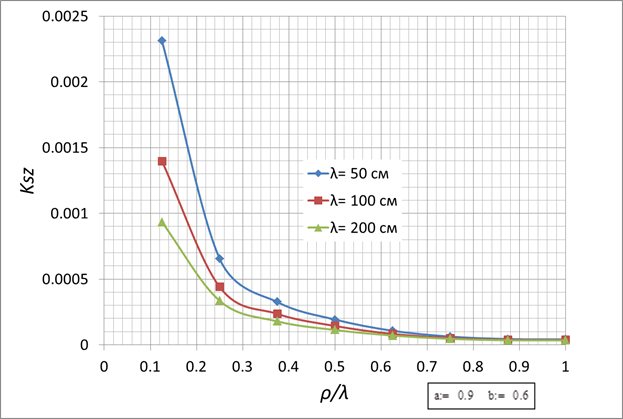
Рис. 7.
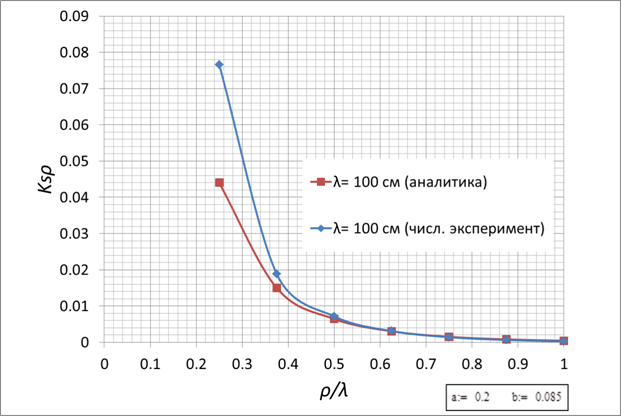

Рис. 8.
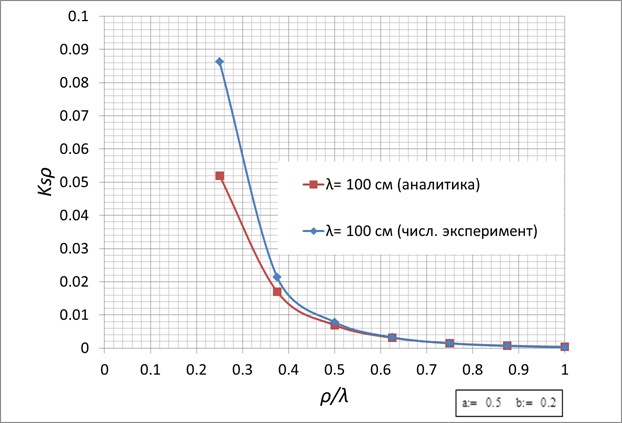

Рис. 9.
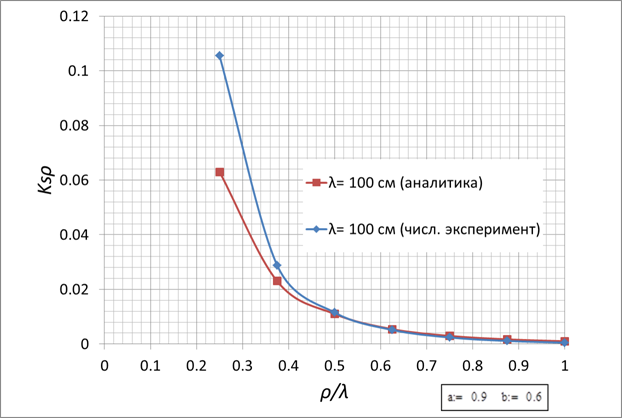
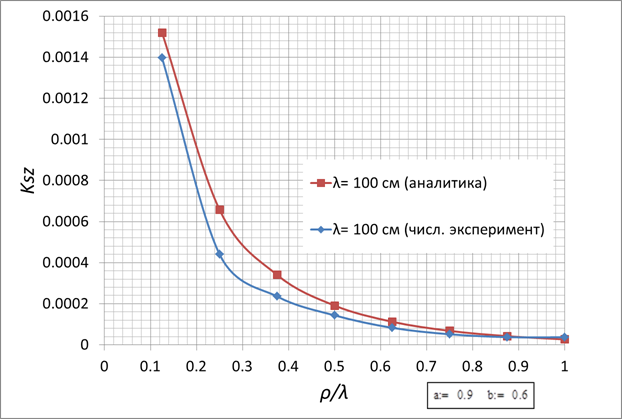
Рис. 10.
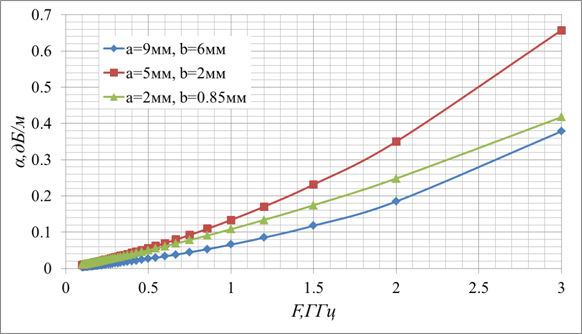
Частотная зависимость тепловых потерь в регулярной
линии Губо-Хармса из медного проводника, покрытого диэлектриком с ![]() для трех параметров линии.
для трех параметров линии.
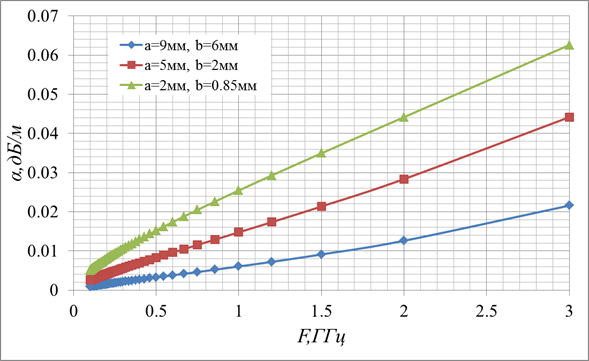
Частотная зависимость тепловых потерь в регулярной
линии Губо-Хармса из медного проводника, покрытого диэлектриком с ![]() для трех параметров линии.
для трех параметров линии.
Рис. 11.

Частотная зависимость тепловых потерь в регулярной
линии Губо-Хармса из алюминиевого проводника, покрытого диэлектриком с ![]() для трех параметров линии.
для трех параметров линии.
Рис. 12.
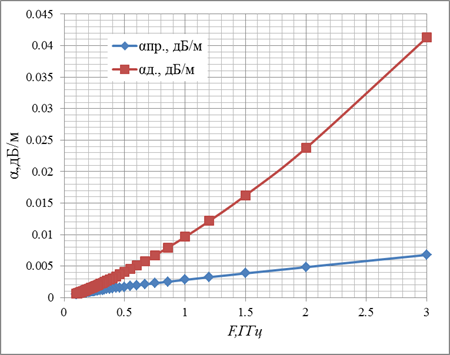
Сравнение частотных зависимостей тепловых
потерь в металлическом проводе ![]() пр. и в диэлектрическом
слое
пр. и в диэлектрическом
слое ![]() д. для провода из медного проводника, покрытого
диэлектриком с
д. для провода из медного проводника, покрытого
диэлектриком с ![]() . a=2мм b=0,85мм.
. a=2мм b=0,85мм.

Сравнение частотных зависимостей тепловых
потерь в металлическом проводе αпр. и в диэлектрическом слое αд. для
провода из медного проводника, покрытого диэлектриком с ![]() .
a=2мм b=0,85мм.
.
a=2мм b=0,85мм.
Рис. 13.
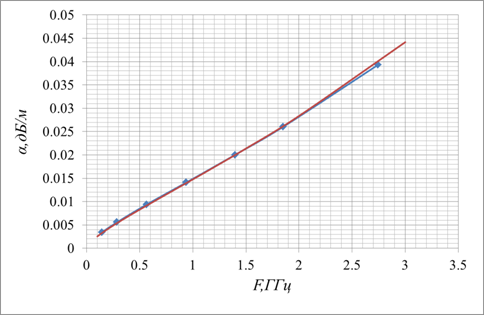
Сравнение частотных зависимостей тепловых потерь в линии Губо-Хармса с медным проводником, с параметрами a/b = 5мм/2мм, рассчитанных по аналитическим формулам и полученных в результате численных экспериментов.
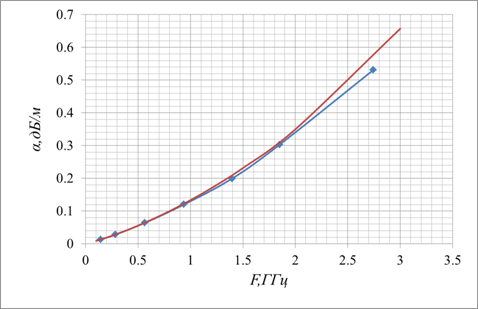
Диэлектрик с ![]() .
Красный- аналитические формулы, синий – численный эксперимент.
.
Красный- аналитические формулы, синий – численный эксперимент.
Диэлектрик с ![]() .
Красный- аналитические формулы, синий – численный эксперимент.
.
Красный- аналитические формулы, синий – численный эксперимент.
Рис. 14.
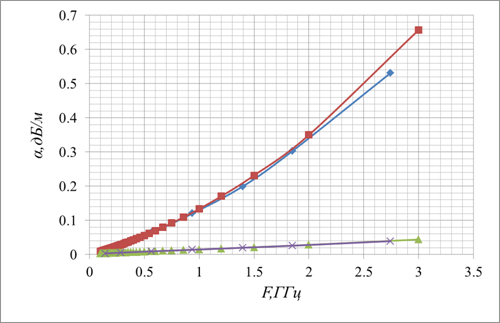
Красный- аналитические формулы, синий –
численный эксперимент для ![]() и зеленый –
аналитические формулы, фиолетовый – численный эксперимент для
и зеленый –
аналитические формулы, фиолетовый – численный эксперимент для ![]() .
.
Рис. 15.
Литература
1. Шевченко В.В. Плавные переходы в открытых волноводах. М.: Наука, 1969.
2. Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь, 1988.
3. Семенов Н.А. Техническая электродинамика. М.: Связь, 1973.
4. Семенов Н.А., Полыковский А.М. Линии поверхностной волны для передачи телевидения. М.: ВЗЭИС, 1964.
