УДK: 621.37/.39;621.38;621.37;621.39
ЭЛЕКТРОДИНАМИЧЕСКИЙ АНАЛИЗ И КОНСТРУКТИВНЫЙ СИНТЕЗ НЕЛИНЕЙНОЙ МИКРОПОЛОСКОВОЙ РЕШЕТКИ С ПОДЛОЖКОЙ ИЗ МЕТАМАТЕРИАЛА
Д.В. Семенихина, Н.И. Чиков, А.И. Семенихин, Н.Н. Горбатенко
Южный Федеральный Университет, г. Таганрог
Статья получена 15 июля 2015 г.
Аннотация. Рассмотрен электродинамический анализ нелинейной микрополосковой решетки с подложкой из метаматериала на основе решения уравнений Максвелла с заданными граничными условиями и условием излучения на бесконечности. Показаны особенности в составлении системы нелинейных интегральных уравнений за счет использования подложки из метаматериала. Представлены численные результаты в виде зависимостей коэффициентов отражения на основной и кратных гармониках от параметров нелинейной нагрузки. Также представлен конструктивный синтез геометрических размеров микрополосковых элементов, позволяющий увеличить эффективность работы отражательной решетки за счет увеличения уровня отраженного поля на кратной гармонике.
Ключевые слова: нелинейное рассеяние, микрополосковые решетки, метаматериалы, электродинамический анализ, конструктивный синтез.
Abstract: The electrodynamic analysis of a nonlinear microstrip lattice with a metamaterial substrate on the basis of the solution of Maxwell's equations with the given boundary conditions and a radiation condition is considered. Singularities in compilation of a system of nonlinear integral equations due to use of a metamaterial substrate are shown. Numerical results are presented in the form of dependences of reflection coefficients on the main and the multiple harmonics from parameters of nonlinear loads. The constructive synthesis of the geometrical sizes of the microstrip elements allowing to increase functioning efficiency of a reflective lattice due to increase of the reflected field on the multiple harmonica is also provided.
Key words: nonlinear scattering , microstrip array, metamaterials, electrodynamic analysis, constructive synthesis.
Введение
Известно, что при облучении электромагнитной волной нелинейных элементов и нелинейных контактов, в спектре отраженного поля появляются частотные составляющие, которые отсутствовали в падающем поле [1]. Структуры с нелинейными элементами способны преобразовывать электромагнитную энергию падающего на них поля в энергию отраженного поля с обогащением спектра сигнала. Они могут использоваться в ретрансляторах для создания скрытых каналов связи, а также для создания маркеров, применяемых для обнаружения терпящих бедствие людей, попавших под завалы или лавины.
Одним из способов реализации устройства с описанными свойствами является использование микрополосковой отражательной решетки, с включенными в нее нелинейными элементами (НЭ) (диоды, транзисторы и др.) [2,3].
В [2,3] рассматривается электродинамическая модель бесконечной периодической микрополосковой структуры, нагруженной на диоды. Микрополосковая решетка располагается на диэлектрическом слое. Недостатком подобной структуры является то, что в спектре отраженного поля уровни кратных гармоник существенно, на десятки децибел, ниже уровня основной гармоники. Для применения в ретрансляторах, маркерах и т.п., требуется разработать устройство, которое бы обеспечивало в спектре отраженного поля уровни кратных гармоник, соизмеримые с уровнем основной гармоники или превышающие его.
После анализа свойств метаматериалов (ММ) [4-9], было выдвинуто предположение, что проблему выравнивания уровней гармоник можно решить применением слоя метаматериала в качестве подложки микрополосковой решетки. Например, в литературе обсуждается использование ММ в антенной технике для миниатюризации антенн [7], повышения частотной избирательности и чувствительности [5], обеспечения требуемых обратных потерь [8] и широкоугольного согласования входного сопротивления микрополосковых антенных решеток в заданной полосе частот [9].
1. Модель периодической микрополосковой структуры с НЭ
За основу математической
модели бесконечной периодической микрополосковой структуры с включенными в нее НЭ,
расположенной на слое ММ (рис.1) взята модель, описанная в [2,3], за
исключением того, что диэлектрический слой заменяется на слой ММ. Структура
представляет собой бесконечную периодическую решетку прямоугольных
микрополосковых элементов. Микрополоски лежат на слое ММ, между полосками включены
НЭ. Ток через них может течь по оси x
или y. Область между экраном
и плоскостью полосков, занятую ММ, обозначаем через V2.
ММ описывается как вещество и характеризуется эффективными проницаемостями ![]() . Внешнюю полубесконечную область
z>0, заполненную
однородной изотропной линейной средой
. Внешнюю полубесконечную область
z>0, заполненную
однородной изотропной линейной средой ![]() обозначаем через V1.
Нелинейные элементы описываются известной полиномиальной вольт-амперной
характеристикой [12]:
обозначаем через V1.
Нелинейные элементы описываются известной полиномиальной вольт-амперной
характеристикой [12]:
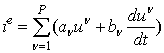 ,
,
где ![]() –
ток, проходящий через нагрузку, u
– напряжение
на ее зажимах,
–
ток, проходящий через нагрузку, u
– напряжение
на ее зажимах, ![]() ,
,
![]() – коэффициенты,
определяемые электрофизическими свойствами нагрузки, P
– степень полинома.
– коэффициенты,
определяемые электрофизическими свойствами нагрузки, P
– степень полинома.
На данную структуру
падает плоская монохроматическая волна с векторами напряженностей
электрического и магнитного полей ![]() частотой ω.
Определяются составляющие рассеянного поля в точке p
на
частотах nω,
где
n – номер частотной
гармоники.
частотой ω.
Определяются составляющие рассеянного поля в точке p
на
частотах nω,
где
n – номер частотной
гармоники.
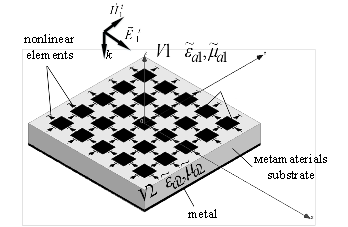
Рисунок 1 – Общий вид микрополосковой структуры
Электродинамический анализ структуры аналогичен приведенному в [1] и основан на решении уравнений Максвелла с заданными граничными условиями и условием излучения на бесконечности.
На поверхности ММ, не занятом нелинейными нагрузками и проводниками, выполняются условия непрерывности касательных составляющих векторов напряженностей электрического и магнитного полей. На поверхности проводников составляющие вектора напряженности электрического поля равны нулю.
Граничные условия на
поверхности нелинейных нагрузок (при z=0), имеющих размеры ![]() , описываются следующими выражениями
[1,2]:
, описываются следующими выражениями
[1,2]:
когда ток течет вдоль x
(![]() ) –
) –
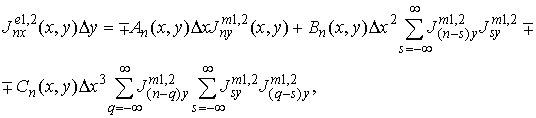
когда ток течет
вдоль y
(![]() ) –
) –
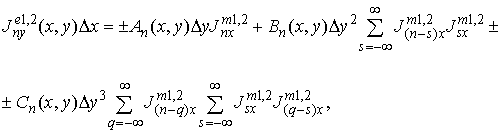
где ![]() -
комплексные амплитуды плотностей поверхностных магнитного и электрического
токов;
-
комплексные амплитуды плотностей поверхностных магнитного и электрического
токов; ![]()
![]() ,
,![]() (an,bn
–параметры
нелинейной нагрузки);
(an,bn
–параметры
нелинейной нагрузки); ![]() - поверхность микрополосковых
элементов в доль оси x
и y
верхний
знак соответствует области V1,
нижний – V2.
- поверхность микрополосковых
элементов в доль оси x
и y
верхний
знак соответствует области V1,
нижний – V2.
Для отыскания полных
полей в областях V1
и V2
вводится вспомогательный магнитный диполь с
координатами (![]() ). Вспомогательный магнитный
диполь возбуждает поле, комплексные амплитуды напряженностей которых обозначаются
через
). Вспомогательный магнитный
диполь возбуждает поле, комплексные амплитуды напряженностей которых обозначаются
через ![]() .
.
Решение задачи проводится
в двух областях – V1
(решается внешняя задача) и V2
(решается внутренняя задача). При составлении интегральных уравнений [10] возникает
трудность, которая отсутствовала при исследовании подобных структур с «обычной»
диэлектрической подложкой. Она связанна с частотной дисперсией
электрофизических параметров ММ [4]. Появляется необходимость в задании
частотной зависимости проницаемостей ![]() и коэффициента
распространения k
в
среде. Поэтому
появляются отличия от системы нелинейных интегральных уравнений (СНИУ), приведенной
в [2].
и коэффициента
распространения k
в
среде. Поэтому
появляются отличия от системы нелинейных интегральных уравнений (СНИУ), приведенной
в [2].
В частности, для решения
вспомогательной задачи определения поля ![]() в
области V2
при
описании магнитного векторного потенциала вводятся частотные зависимости
в
области V2
при
описании магнитного векторного потенциала вводятся частотные зависимости ![]() :
:
![]()
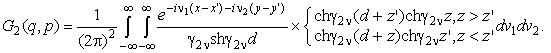
Здесь,![]() - функция Грина
плоскопараллельного волновода;
- функция Грина
плоскопараллельного волновода; ![]()
![]() .
.
Следовательно, выражения для векторов напряженностей вспомогательного электрического и магнитного полей в области V2 также будут иметь несколько другой вид.
Вывод интегральных соотношений для полей
основан на применении леммы Лоренца для рассеянных полей, записанной для каждой
спектральной компоненты и применении граничных условий [12]. В
итоге получается бесконечная СНИУ относительно поверхностных токов![]() :
:
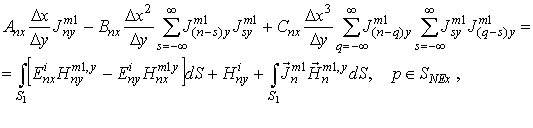
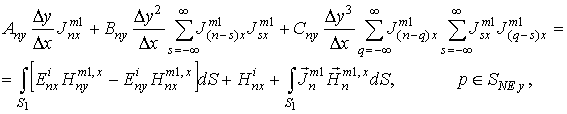
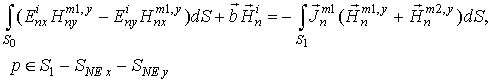 .
.
Здесь ![]() - поверхность ММ при z=0.
- поверхность ММ при z=0.
Затем, на основе условия периодичности решетки, выводится система уравнений относительно поверхностных токов на одном периоде решетки. Далее, по методу Крылова-Боголюбова, задача сводится к системе нелинейных алгебраических уравнений, которая решается методом Бройдена [11].
2. Численные результаты
При численном решении задачи нелинейные
нагрузки полагаются безинерционными;
ВАХ представляется полином третьей степени ![]() .
В
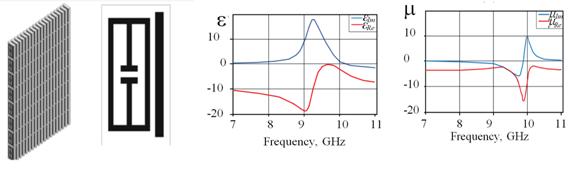
качестве ММ берется структура, описанная в [5]. Структура ММ и его частотные
зависимости параметров εeff,
μeff
показаны на рисунке 2.
.
В
качестве ММ берется структура, описанная в [5]. Структура ММ и его частотные
зависимости параметров εeff,
μeff
показаны на рисунке 2.
(а) (б) (в) (г)
Рисунок 2 ––Фрагмент слоя ММ (а); структура одиночного элемента ММ (б); эффективная диэлектрическая проницаемость ММ (в); эффективная магнитная проницаемость ММ (г)
Реальные части эффективных проницаемостей εeff, μeff имеют отрицательные значения в диапазоне частот, что соответствует DNG-материалу (Double Negative).
Численные результаты представляются ниже в виде зависимостей модулей коэффициентов отражения полей на кратных гармониках от параметров нелинейных нагрузок a1 и a2 (зависимость от a3 не приводится, так как вклад от этого параметра незначителен). Под коэффициентом отражения |Rn| на частоте n-й гармоники здесь понимается отношение модуля напряженности отраженного поля на кратной гармонике к модулю напряженности падающего поля на основной частоте.
Частота падающей волны 9.95 ГГц. Эффективные значения диэлектрической и магнитной проницаемостей на этой частоте согласно [5] равны ε2= –1.57, μ2= –2.35 . Для определения влияния ММ расчет проводится также для модели аналогичной структуры, в которой подложка представлена обычным диэлектриком. В качестве диэлектрика берется материал FR-4 (ε2,= 4.4, μ2= 1). На рисунке 3 приведены результаты численного эксперимента. Как видно, при определенных значениях параметров нелинейных нагрузок (при a2=0.002, a1=0.00105; a1=0.019, a2=0.0445) происходит существенное подавление уровня отраженного поля на основной гармонике.
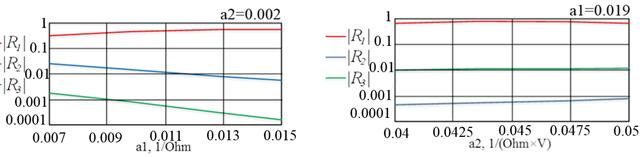
(а) (б)
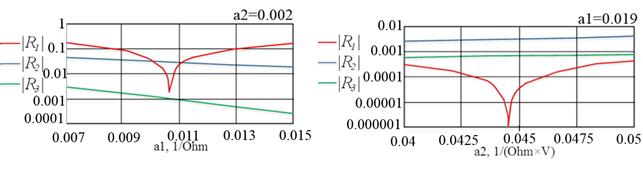
(в) (г)
Рисунок 3 – Зависимости коэффициентов отражения от параметров нелинейных нагрузок (а, б – подложка из FR-4; в, г – подложка из ММ)
Подобрав значения a1 и a2, можно получить в спектре отраженного сигнала вторую и третью гармоники, соизмеримые по уровню с основной гармоникой или превышающие ее. Стоит отметить, что выравнивание уровней сигналов на кратных гармониках происходит благодаря подавлению основной гармоники, т.е. нет существенного изменения в характере поведения коэффициентов отражения на кратных гармониках при использовании ММ, поскольку на кратных частотах электрофизические параметры ММ соответствуют параметрам обычного диэлектрика (FR-4). Подавление основной гармоники происходит из-за того, что при определенных условиях активная составляющая поверхностного импеданса Z на слое ММ возрастает до 377 Ом, а мнимая часть равна нулю [5], что соответствует известным термодинамическим ограничениям, накладываемым на пассивный импеданс пассивных структур [12].
3. Конструктивный синтез геометрических размеров микрополосковой решетки
Для увеличения эффективности описанного выше устройства проводится конструктивный синтез геометрических размеров микрополосковой решетки. Расчет структуры выполняется методом конечных элементов при линейной аппроксимации ВАХ нелинейных нагрузок. Модель содержит фрагмент микрополосковой решетки, с подложкой из ММ (рисунок 4). В данной задаче модель ММ описывается не веществом, а структурой, показанной на рисунке 2a. Фрагмент структуры является каналом Флоке. При падении поля на данную структуру происходит возбуждение НЭ на второй и третьей гармониках. Таким образом, НЭ выступают в качестве источников. Поэтому в данной задаче на месте НЭ установлены источники (порты) гармонических колебаний на частотах кратных гармоник (рисунок 4).
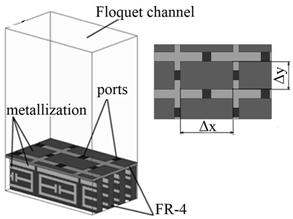
Рисунок 4 – Канал Флоке
Расчеты зависимости напряженности электрического поля в дальней зоне от геометрических размеров микрополосков Δx, Δy на второй и третьей гармониках (рисунки 5, 6) показывают, что имеются геометрические размеры Δx, Δy, при которых рассеянное поле на частоте третьей гармоники имеет явный экстремум. Используя полученные данные можно увеличить эффективность работы нелинейной микрополосковой решетки на кратных гармониках.
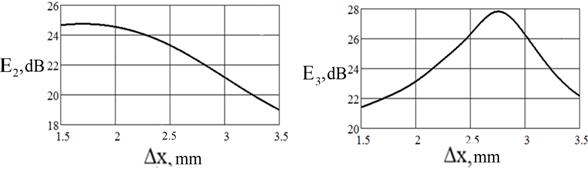
(а) (б)
Рисунок 5 – Зависимость интенсивности поля от Δx: отраженное поле на второй гармонике(а); отраженное поле на третьей гармонике (б)
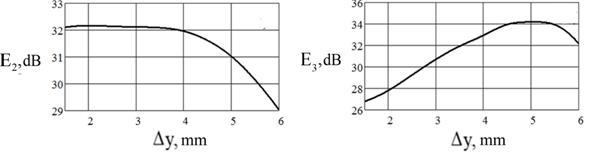
(а) (б)
Рисунок 6 – Зависимость интенсивности поля от Δy : отраженное поле на второй гармонике(а); отраженное поле на третьей гармонике (б)
4. Выводы
В результате проведенной работы было установлено, что применение ММ в нелинейных микрополосковых решетках в качестве подложки способствует выравниванию уровней кратных гармоник в сравнении с основной гармоникой в отраженном поле. Это достигается за счет подавления уровня основной гармоники в отраженном поле. Конструктивный синтез позволяет определить геометрические размеры микрополосков, при которых отражательная решетка будет работать эффективнее за счет увеличения уровня отраженного поля на кратной гармонике.
Литература
1. Штейншлегер В.Б. Нелинейное рассеяние радиоволн металлическими обьектами// Успехи физических наук, 1984. Т.141. Вып.1. С.131-145.
2. Семенихина Д.В., Гамолина И.Э. Рассеяние плоской электромагнитной волны бесконечной периодической микрополосковой нелинейно нагруженной структурой //Радиотехника и электроника, 2000. Т.45, №5. С.552-556.
3. Семенихина Д.В. Возбуждение решетки нелинейных нагрузок на идеально проводящем экране , покрытом диэлектриком// Изв.Вузов. Радиофизика, 2001, №7, с. 592-599.
4. Веселаго В. Г. Электродинамика материалов с отрицательным коэффициентом преломления // Успехи физических наук, 2003. Т. 173. № 7. С. 790-794.
5. H.-M. Lee, H.-S. Lee. А metamaterial based microwave absorber composed of coplanar electric-field-coup-led resonator and wire array.// Progress In ElectromagНЭtics Research C, Vol. 34, 111{121}, 2013.
6. Wu M.F., Meng F.Y., Wu Q., Wu J , Lee J.C. An approach for small omnidirectional microstrip antennas based on the backward waves of double negative metamaterials// Appl. Phys. A 87, 193–198.2007.
7. Singh G. Double Negative Left-Handed Metamaterials for Miniaturization of Rectangular Microstrip Antenna// J. Electromagnetic Analysis & Applications, No 2, PP. 347-351. 2010.
8. Mahdy M. R. C., Zuboraj M. R. A., Ovi A. A. N. , Matin M. A., A Novel Design Algorithm And Practical Realization of Rectangular Patch Antenna Loaded with SNG Metamaterial// Progress In Electromagnetics Research M, Vol. 17, PP. 13-27, 2011.
9. Lei Xing, Qian Xu, Jing Li, Zhixia Wei, Jun Ding, Chenjiang Guo Broaden the Bandwidth of Patch Antenna by Using Inhomogeneous Metamaterial Substrate// Progress In Electromagnetics Research Symposium Proceedings, Xi'an, China, March 22-26, 2010.
10. Чиков Н.И. Электродинамическое моделирование отражающей нелинейной микрополосковой структуры с использованием DNG-материала в качестве подложки//Изв. ЮФУ. Технические науки, 2013, c 135-141.
11. Mordecai A. Nonlinear Programming: Analysis and Methods. — Dover Publishing, 2003, 332рр.
12. Capek V., Sheehan D.P. Challenges to The Second Law of Thermodynamics: Theory and Experiment (Fundamental Theories of Physics), Springer, Dordrecht, Netherlands, 2010. 366 pp.