| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6 , 2000 |
ДИФРАКЦИЯ ПЛОСКОЙ
ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
НА ПОЛОМ ДИЭЛЕКТРИЧЕСКОМ КОНУСЕ
Л.М. Минокин
Получена 26 июня 2000 г.
Рассмотрен уточненный метод расчета электромагнитного поля внутри полого диэлектрического конуса на основе решения интеграла Кирхгофа и метода стационарной фазы. Разработан метод измерения и приведены экспериментальные результаты распределения амплитуды электромагнитного поля внутри полого диэлектрического конуса.
ВВЕДЕНИЕ
Методы расчета и измерения распределения электромагнитного поля внутри полого диэлектрического конуса представляют практический интерес например для разработчиков антенных обтекателей (АО) летательных аппаратов [1]. Разработка таких методов позволяет лучше понять физику явления прохождения электромагнитных волн через диэлектрические оболочки и сократить сроки и стоимость проектирования системы антенна-обтекатель. Цель данной работы уточнение метода расчета электромагнитного поля и сопоставление рассчитанных значений (различными методами) и экспериментальных данных.
ЧАСТЬ ПЕРВАЯ. МЕТОД РАСЧЕТА
В силу больших математических сложностей строгого решения задачи расчета электромагнитного поля внутри антенного обтекателя до настоящего времени не разработано. На наш взгляд наиболее приемлемое решение получено в работе [2] на основе асимптотического решения интеграла Кирхгофа и метода стационарной фазы.
В этой работе поле на внутренней поверхности конуса определяется по формулам геометрической оптики [3], считая, что прохождение каждого луча через стенку диэлектрического конуса определяется как для бесконечного плоского слоя.
Значение вектора электромагнитного поля в произвольной точке наблюдения
N со значением вектора на внутренней границе замкнутой поверхности S окружающей эту точку определяется решением интеграла Кирхгофа [4]. Считая диэлектрический полый конус замкнутым на бесконечности, возможно применение этого интеграла для решения данной задачи:где
![]() –
векторы электрического и магнитного поля,
–
векторы электрического и магнитного поля,
S– поверхность интегрирования,
![]() –
нормаль в точке пересечения с конусом,
–
нормаль в точке пересечения с конусом,
![]() –
радиус-вектор точки наблюдения,
–
радиус-вектор точки наблюдения,
![]() –
магнитная проницаемость среды,
–
магнитная проницаемость среды,
G– функция Грина,
![]() –
расстояние
между точкой наблюдения и текущей точкой на
внутренней поверхности,
–
расстояние
между точкой наблюдения и текущей точкой на
внутренней поверхности,
k– волновое число,
![]() –
длина волны.
–
длина волны.
В работе [2] окончательное выражение для поля в точке наблюдения на основе асимптотического решения интеграла Кирхгофа получено в следующем виде:
При нахождении этого решения автор работы [2] использует вклады от двух стационарных точек, одна из них находится на действительном конусе
S1, а вторая на мнимом конусе S2 (что, строго говоря, не соответствует реальной физической картине). При этом пределы интегрирования по переменной j раздвигаются в бесконечность, что фактически превращает задачу дифракции на полом конусе в задачу дифракции на полом клине.Принятые в данной статье обозначения и постановка задачи (рис. 1,2,3) как и формулы описывающие геометрию полого диэлектрического конуса, повторяют обозначения, постановку задачи и формулы работы [2]. Дополнительно в данной статье введена координата крена j
(рис.2) и два новых ортаРис.1
Рис.2
Рис. 3
По нашему мнению более корректно, применить метод стационарной фазы одновременно для функции от двух переменных, а пределы интегрирования по j брать физически реальные ± p
.Таким образом, необходимо вычислить интеграл следующего вида:
Будем применять метод стационарной фазы для функции от двух переменных сразу. Обозначим:
![]() (6)
(6)
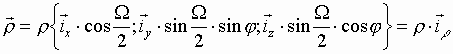 .
.
Здесь
Точки стационарной фазы определяются из условия:
Находим:
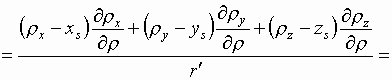
(9)
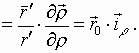
Получаем:
Аналогично находим:
Таким образом, стационарные точки должны удовлетворять условию:
Эти условия удовлетворяются в двух случаях:
где
Первый случай соответствует точке пересечения прямой, проведенной из точки наблюдения параллельно вектору падающего поля, с поверхностью АО. Второй случай соответствует равенству угла падения и угла отражения. Это было отмечено и в работе [2].
Разложим функцию
В этом выражении второй член ряда равен нулю (условие стационарности), поэтому:
Здесь
Вычисление производных дает:
Применяя метод стационарной фазы к вычислению интеграла
Нами были проведены численные расчеты коэффициентов
Здесь
![]()
В качестве пути интегрирования по
r выберем для первой стационарной точки от –¥ доДля первой стационарной точки:
Для второй стационарной точки:
Как можно заметить
, проекции пути интегрирования на плоскость, проведенную через вершину полого конуса перпендикулярно направлению падения поля, одинаковы (как и в работе [2]).Пределы интегрирования по координате
j выберем как ± p , тогда при замене переменных пределы интегрирования по v примут значения:Тогда для первой стационарной точки:
Для второй стационарной точки:
Все три интеграла в правых частях выражений (25) и (26) переходят в интегралы Френеля вида:
После преобразований получаем значение напряженности электрического поля в точке наблюдения:
где
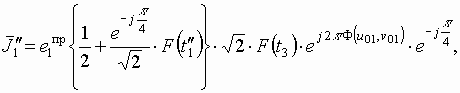
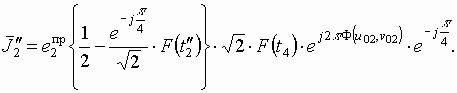
Здесь
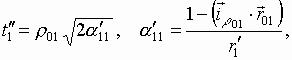
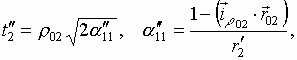
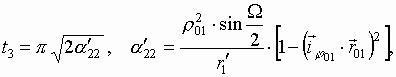
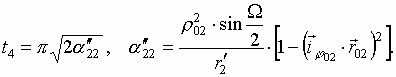
Как можно заметить, в частных случаях при раздвижении пределов интегрирования по координате j в бесконечность
Для большей наглядности приведем пример расчета амплитудного и фазового распределения поля по формулам геометрической оптики, по формулам работы [2] и по формулам полученным автором данной статьи. Пусть антенный обтекатель представляет собой полый диэлектрический конус постоянной толщины с относительными к длине волны размерами, показанными на рис.4.
Рис.4
Пусть диэлектрическая проницаемость и тангенс угла диэлектрических потерь соответственно равны e
= 3,42 ; tgd = 0,01. Определим поле в центральном сечении антенного обтекателя в 13 точках, при угле отворота антенны a = 8 градусов.На рис.5 и 6 показаны рассчитанные значения соответственно квадрата модуля коэффициента прохождения и фазового набега для трех случаев: 1 – метод геометрической оптики, 2 – метод разработанный в работе [2], 3 – метод автора данной статьи.
Рис.5
Рис.6
Как видно из рисунков, основой решения является метод геометрической оптики. Учет конечных пределов интегрирования приводит к большей амплитуде осцилляций кривых как по амплитуде, так и по фазе.
Из опыта использования различных методов расчета считаем, что наиболее перспективным направлением дальнейшего развития методов расчета применительно к антенным обтекателям хорошей аэродинамической формы является использование математического аппарата на основе численного решения известного интеграла Кирхгофа. При этом пределы интегрирования по внутренней поверхности произвольной оболочки антенного обтекателя должны выбираться реальными (в том числе и по координате крена). Пример определения поверхности интегрирования для произвольного угла отворота показан на рис.7. Так, например, сделано в работе [5].
Рис.7
ЧАСТЬ ВТОРАЯ. РЕЗУЛЬТАТЫ ИЗМЕРЕНИЯ АМПЛИТУДНОГО РАСПРЕДЕЛЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ ВНУТРИ АНТЕННОГО ОБТЕКАТЕЛЯ
ОБЪЕКТ ИССЛЕДОВАНИЯ
В качестве объекта исследования был выбран макет антенного обтекателя (АО) из кварцевой керамики в виде полого диэлектрического конуса. Диэлектрические характеристики материала: диэлектрическая проницаемость e = 3,42; тангенс угла диэлектрических потерь tgd = 0,005. Геометрические размеры конуса: длина – 652 мм, диаметр у основания – 274 мм, толщина стенки – 10 мм.
ОПИСАНИЕ ИЗМЕРИТЕЛЬНОЙ УСТАНОВКИ И МЕТОДИКА ИЗМЕРЕНИЙ
Функциональная схема измерительной установки приведена на рис.8. Установка состоит из генератора СВЧ – 1, передающей антенны линейной поляризации – 2, приемной антенны линейной поляризации – 3, измерительного СВЧ приемника – 4, антенного обтекателя – 5, механизма перемещения антенного обтекателя – 6.
Рис.8
Передающая и приемная антенны расположены неподвижно на радиолинии – 7. Выбор приемной антенны должен был отвечать условию обеспечения наиболее широкой диаграммы направленности в обоих плоскостях и наименьшему раскрыву. В качестве приемной антенны был выбран сужающийся открытый конец волновода, заполненный диэлектриком с большим значением диэлектрической проницаемости. Раскрыв приемной антенны в длинах волн составлял примерно 0,27l ´ 0,27l . Измеренные диаграммы направленности приемной антенны в E и H плоскостях показаны на рис.9.
Рис.9
Расстояние между передающей и приемной антеннами соответствовало условию дальней зоны. Измерения распределения амплитуды электромагнитного поля проводились в сечении АО на расстоянии 160 мм от торца.
Антенный обтекатель перемещался в горизонтальном направлении перпендикулярно радиолинии (параллельно самому себе), и отворачиваться на произвольные углы, относительно радиолинии. Кроме того установка позволяла перемещать антенный обтекатель вверх и вниз относительно радиолинии на фиксированную величину (± a). При измерении фиксировались уровни сигнала принимаемого антенной зонда (Pi), относительно уровня сигнала без антенного обтекателя (P0). Все измерения проводились в безэховой камере.
Конструкция механизма перемещения антенного обтекателя выбиралась также из условия минимального влияния механизма перемещения на распределение электромагнитного поля в измеряемом сечении. Экспериментально определялось влияние механизма перемещения, при сканировании в выбранном сечении (без антенного обтекателя), на уровень принимаемого сигнала.
Экспериментальные данные влияния механизма перемещения АО приведены на рис.10. Измерения проводились в E и H плоскостях. По оси абсцисс отложено расстояние перемещения механизма (без антенного обтекателя) в поперечной плоскости, относительно радиолинии, по оси ординат – относительное изменение мощности принимаемого сигнала (Pi) к его максимальному значению (Pmax).
Рис.10
РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТА
1. Результаты измерений
распределения амплитуды поля (относительной
мощности принимаемого сигнала) в основном
сечении АО при трех углах отворота АО (0,-10, 10
градусов) приведены на рис.11.Случай
измерения соответствует горизонтальной
поляризации, и относительной толщины
стенки к длине волны ![]() =
0,3380.
=
0,3380.
Рис.11
2. На рис.12 приведены результаты измерений распределения амплитуды поля (относительной мощности принимаемого сигнала) при различных соотношениях длины волны к толщине стенки: 1 кривая – 0,3134, 2 – 0,3127, 3 – 0,3137, 4 – 0,3140, 5 – 0,3130 при горизонтальной поляризации поля.
Рис.12
3.На рис.13 приведены результаты измерений распределения амплитуды поля (относительной мощности принимаемого сигнала) при соосном положении АО и при трех значениях высоты оси АО a = 0, a = 10 мм (выше радиолинии) и a = -10 мм (ниже радиолинии).
Рис.13
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ
Как видно из рис. 5, 6, 11, 12 и 13 распределение поля имеет явно выраженный дифракционный характер. Наиболее сильное изменение распределения поля наблюдается на углах отворота близких к половине угла при вершине диэлектрического конуса (так называемых "скользящих углах"). Наблюдается симметричный переворот кривых при смене знака угла отворота (рис.11).
Изменение рабочей частоты в диапазоне частот 0,4 % приводит к смещению кривых амплитудных распределений параллельно самим себе, не изменяя при этом принципиально вид дифракционной картины (рис.12).
Наибольшая изрезанность кривой наблюдается в основном сечении (a = 0). При смещении диэлектрического конуса (антенного обтекателя) вверх либо вниз на одну и ту же величину зависимости амплитудных распределений приблизительно повторяют друг друга (рис.13).
При сопоставлении рассчитанных и экспериментальных значений необходимо пояснить, что расчет производился для диэлектрического конуса бесконечных размеров, в то время как эксперимент проводился на реальном объекте с ограниченными размерами, кроме того в отличии от расчета поля в точке наблюдения, реальная антенна-зонд имела определенный (хотя и небольшой) раскрыв. Несмотря на это качественно результаты расчета и эксперимента совпадают.
ВЫВОДЫ
Разработан уточненный метод расчета электромагнитного поля внутри полого диэлектрического конуса на основе решения интеграла Кирхгофа и метода стационарной фазы. Приведены экспериментальные данные, подтверждающие дифракционный характер распределения электромагнитного поля внутри полого диэлектрического конуса.
ЛИТЕРАТУРА
1. Минокин Л.М. Антенные обтекатели зенитных ракет. – "Антенны", выпуск 2 (39), 1997, с. 79-86.
2. Измайлов Ф.Ф. Применение метода Кирхгофа для асимптотического решения задачи дифракции плоской волны на диэлектрических телах вращения, Сб. "Антенны", вып.12, изд. "Связь", 1971, с.13-24.
3. Борн М., Вольф Э. Основы оптики, пер. с англ., М., 1973, с.74-75.
4. Стрэттон Дж. Теория электромагнетизма, пер. с англ., М.-Л., 1948, с.411.
5. Колосов Ю.А., Левков Ф.Е. Расчет влияния криволинейных диэлектрических структур на характеристики направленности излучающих систем в приближении физической оптики, Радиотехника и электроника, 1996, том 41, № 6, с. 655-660.