|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6 , 2000 | |
ВОЗБУЖДЕНИЕ ИМПЕДАНСНОЙ
ПОВЕРХНОСТИ ЦИЛИНДРА
ПРОДОЛЬНЫМ ЭЛЕКТРИЧЕСКИМ ДИПОЛЕМ
Габриэльян
Д.Д., Звездина М.Ю.,
Костенко П.И.,
Ростовский военный институт ракетных войск
Получена 25 июня 2000 г.
Анализируются закономерности распределения токов на импедансной поверхности кругового цилиндра, возбуждаемой продольным электрическим диполем. Приводятся соотношения и результаты исследований распределения поверхностных токов при различных значениях импеданса.
Исследование вопросов, связанных с нахождением полей и токов в излучающих системах, электромагнитной совместимостью и неразрушающим контролем радиоэлектронной аппаратуры, требует знания распределения полей в ближней зоне. Основой рассмотрения указанных вопросов является решение представляющей во многих случаях и самостоятельный интерес задачи о нахождении поля электрического или магнитного диполя, расположенного вблизи поверхности тела
[1].Возбуждение импедансных поверхностей электрическими и магнитными диполями для ряда случаев рассмотрено в работах
[2-5]. Однако существенного продвижения в анализе закономерностей влияния собственно импедансной поверхности на излучение диполя удается добиться, когда решение задачи может быть представлено в замкнутой форме. Последнее возможно для тел, поверхность которых совпадает с координатной поверхностью, допускающей разделение переменных в волновом уравнении.Исходя из вышесказанного, целью статьи является решение задачи о нахождении поля продольного электрического диполя, расположенного вблизи импедансной поверхности кругового цилиндра.
Рассмотрим однородный и безграничный вдоль оси
круговой цилиндр радиуса 
с поверхностным импедансом 
,
возбуждаемый продольным электрическим
диполем (рис.1). Ток в диполе с
длиной плеча 
определяется выражением
где
- координаты центра диполя.
Выражения для
-составляющих
электрического и магнитного полей,
создаваемых электрическим током (1), имеют
вид [2]
где
- электрический векторный потенциал; 
- волновое число; 
- длина волны; 
Ом – волновое сопротивление свободного
пространства; 
- радиус-вектор произвольной точки; 
- мнимая единица. Сомножитель 
,
описывающий зависимость всех величин от
времени, опущен.
Отличная от нуля продольная компонента электрического векторного потенциала может быть описана с использованием представления функции Грина свободного пространства в цилиндрической системе координат
[6]:
где
;
;
-го
порядка и функции Ганкеля 2-го рода -го
порядка.
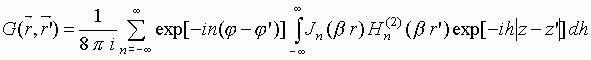После подстановки выражения (3) в соотношения (2) последние принимают вид
где
Поскольку электродинамические и геометрические параметры цилиндра не зависят от координаты z, решение задачи будем искать в предположении, что рассеянное поле имеет такую же зависимость от данной координаты, как и в падающем поле:
Коэффициенты
,
описывающие дифракцию волны на импедансном
круговом цилиндре, могут быть найдены из
граничных условий 
[6]:
В соотношении (7) поперечные компоненты электрического и магнитного полей в соответствии с
[6] представляются через продольные компоненты полягде
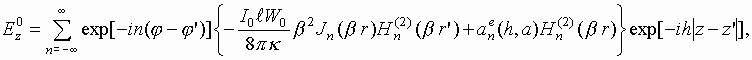
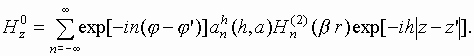
С учетом соотношений (7) и (8) коэффициенты
,
как было показано в [7], описываются
выражениями
Как было показано в
[8,9], при анализе поля в ближней зоне трудно получить численные результаты по данным формулам. Поэтому в соответствии с предложенным там же и использованном в [10] для данного вибратора подходом преобразуем приведенные выше выражения в форму интеграла по комплексному переменному с соответствующей деформацией первоначального пути интегрирования (рис.2). Выполнив преобразования, подробно описанные в [8], можно записать следующие выражения для продольных компонент электрического и магнитного полей:где * - символ комплексного сопряжения;
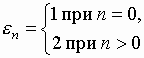- числа Неймана;
Из формулы (11) следует, что для частного случая идеально проводящей поверхности (
)
коэффициент 
и, соответственно, 
.
С использованием соотношений (8), (14)-(16) несложно получить выражения, описывающие поперечные компоненты ближнего поля продольного диполя, расположенного вблизи однородного и безграничного вдоль оси
импедансного кругового цилиндра. На основе
данных соотношений можно также получить и
выражения, позволяющие вычислять
возбуждаемые на поверхности цилиндра
электрический и магнитный поверхностные
токи:
где
- единичные координатные векторы
цилиндрической системы координат;
-компонента
вектора напряженности магнитного поля при
вычислении поверхностного тока (случай 
)
описывается соотношением:
.
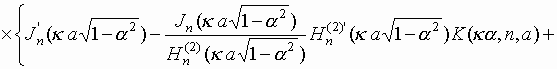
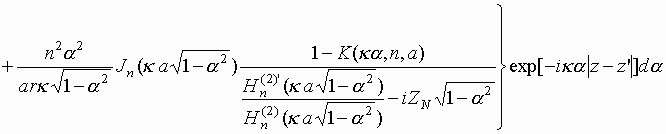Продольная компонента
вычисляется в соответствии с формулой (14)
при условии 
.
Прежде, чем обращаться к результатам численных исследований распределения плотности поверхностного тока, проведем качественный анализ возникающих особенностей. Из формул (14)-(16) следует, что, если для
поверхностный ток имеет только 
-компоненту,
то на импедансной поверхности существуют
как продольная, так и поперечная компоненты.
При этом в направлении оси 
амплитуда поверхностного тока, как для
продольной, так и для поперечной компонент,
затухает по экспоненциальному закону.
Однако в поперечной плоскости характер
распределения данных компонент является
различным. Так, если для основной (продольной)
компоненты максимальное значение
плотности поверхностного тока
соответствует точке, наименее удаленной от
диполя, то для поперечной компоненты
поверхностного тока максимум наблюдается
при углах 
,
близких к 
,
а в сечениях цилиндра плоскостью,
проходящей через оси диполя и цилиндра,
величина -компоненты
поверхностного тока обращается в нуль.
Максимум плотности полного поверхностного
тока, как и в случае падения плоской волны,
приходится на ближайшую к диполю точку
поверхности, что характерно и для
импедансных плоскостей [3].
Результаты исследований распределения плотности поверхностного тока, возбуждаемого электрическим диполем, удаленным на расстояние
от кругового цилиндра радиуса 
,
для различных значений поверхностного
импеданса, представлены на рис.3-8.
На всех иллюстрациях с индексом "а"
показано распределение модуля 
-компоненты
поверхностного тока, с индексом "б" –
модуля -компоненты,
а с индексом "в" – модуля полного
поверхностного тока. При проведении
расчетов рассматривался случай
расположения диполя на оси 
(
).
Значения поверхностного импеданса
принимались соответственно равными 
,
, 
,
, 
,
(рис.3-8). С учетом
симметрии законов распределения
поверхностного тока как относительно
продольной, так и азимутальной координат,
на рисунках приводятся только данные,
соответствующие 
и 
.
Полученные распределения нормированы к
максимальному значению плотности
поверхностного тока на идеально проводящем
цилиндре.
Как следует из приведенных результатов, размещение диполя вблизи импедансной цилиндрической поверхности приводит к эффективному взаимодействию поля с импедансной структурой, что выражается в возбуждении поверхностных волн, амплитуды которых существенным образом зависят как от величины импеданса, так и от кривизны поверхности. Сказанное подтверждается сопоставлением результатов, приведенных на рис.3-8.
Наличие поверхностного импеданса по-разному сказывается и на амплитуде продольной и поперечной компонент поверхностного тока. Так, переход от индуктивного к емкостному импедансу приводит к увеличению амплитуды основной компоненты и уменьшению поперечной компоненты. При этом если для индуктивного импеданса в поперечном направлении не наблюдается возбуждения поверхностных волн, о чем свидетельствует отсутствие осцилляций в распределении тока, то в случае емкостного поверхностного импеданса существуют поверхностные волны, что подтверждается наличием резко выраженных осцилляций.
При отрицательном активном импедансе происходит значительное увеличение как продольной, так и поперечной компонент поверхностного тока, а также возбуждение поверхностных волн. Изменение знака поверхностного импеданса приводит к уменьшению амплитуд обеих компонент и уменьшению амплитуд поверхностных волн. Для выбранного случая смешанного импеданса как положительная активная, так и отрицательная реактивная части приводят к уменьшению амплитуды обеих компонент плотности поверхностного тока, а также к уменьшению амплитуды поверхностных волн.
Таким образом, полученные соотношения и представленные результаты численных исследований позволяют выявить основные закономерности в распределении поверхностных токов на импедансных цилиндрах, возбуждаемых продольными электрическими диполями.
Рис.3 (
)
|
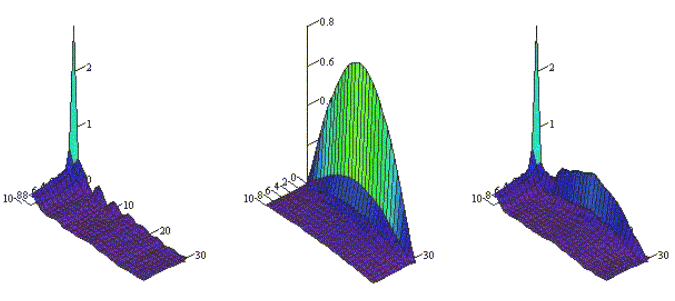
а) |
б) |
в) |
Рис.6 (
)
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
Авторы:
Габриэльян Дмитрий Давидович – д.т.н.
профессор, РВИ РВ,
Звездина Марина Юрьевна – к.т.н., РВИ РВ,
 |
 |
,
(1)
(2)
,
(3)
(4)
.
(5)
.
(6)
(7)
(8)
,
(9)
,
(10)
,
(11)
(14)
(15)
(16)
(17)
(18)
