"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6, 2002

ИНТЕРФЕРЕНЦИОННЫЕ ЭФФЕКТЫ В ДВУМЕРНО-ПЕРИОДИЧЕСКИХ ДИФРАКЦИОННЫХ РЕШЕТКАХ

Ветлужский А.Ю., e-mail: vay@ofpsrv.bsc.buryatia.ru

Отдел физических проблем при Президиуме

Бурятского научного центра СО РАН

Получена 15 июня 2002 г.

Рассмотрена дифракция электромагнитных волн на двумерно-периодической решетке, образованной бесконечно протяженными цилиндрическими элементами малого поперечного сечения. Показано, что ранее обнаруженный эффект «прозрачности» таких структур, заключающийся в превышении значениями уровня поля в решетке соответствующих его значений в отсутствие структуры и наблюдающийся при определенных параметрах решетки, связан с интерференцией падающей волны и волн, однократно рассеянных на элементах из ближайшей окрестности погруженной в структуру точки наблюдения.

Дифракционные решетки различной геометрии широко используются в различных радиотехнических устройствах, а также для моделирования искусственных и естественных дискретных сред. В настоящее время достаточно полно исследованы свойства одномерно-периодических решеток [1], создана строгая теория дифракции волн на таких структурах. Однако свойства объемных, в частности, двумерно-периодических решеток остаются изученными недостаточно. В особенности это относится к специфическим эффектам, сопровождающим рассеяние волн на таких структурах и не имеющим аналогов при дифракции на одномерных решетках.

Так, в работах [2,3] было показано, что при дифракции электромагнитных волн на двумерно-периодических решетках, образованных круговыми идеально проводящими и импедансными бесконечно длинными цилиндрами, при определенных соотношениях между периодом размещения элементов и длиной волны практически в любом месте структуры (за исключением областей, непосредственно примыкающих к рассеивающим элементам) имеет место усиление поля по сравнению с его уровнем в свободном пространстве. Наиболее интересным является то, что данный эффект проявляется при любом количестве элементов, образующих объемную двумерную решетку, что позволяет говорить о возможности его наблюдения в структурах любой протяженности, в том числе и в неограниченных дискретных средах. Второй важный момент, на который обращалось внимание в данных работах, заключается в том, что указанный эффект имеет место практически при любом удалении источника поля относительно границы структуры и в широких пределах изменения поперечных размеров элементов.

Цель настоящей работы заключается в анализе физических механизмов, лежащих в основе данного эффекта.

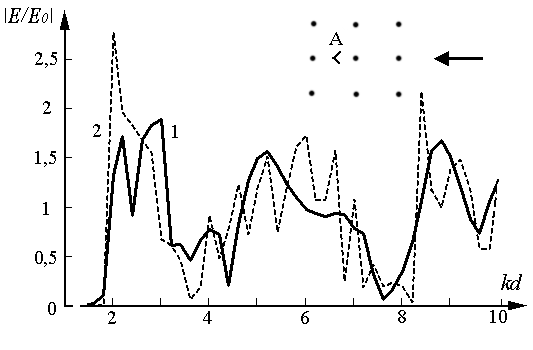
Обратимся к рис. 1, где представлены рассчитанные по методике, изложенной в [2], зависимости относительного уровня поля от безразмерного параметра kd.

Рис. 1

Здесь E – напряженность поля в структуре, Е₀ – в свободном пространстве, - длина волны, d – период решетки, одинаковый для двух ортогональных направлений. Радиус цилиндров а = 0,03λ. Структура возбуждается плоской волной, точка наблюдения расположена на расстоянии d/2 от центрального элемента решетки. Ряды идеально проводящих цилиндрических элементов расположены вдоль (или, что то же, поперек) направления прихода падающей волны (см. вставку в рисунок, где А - точка наблюдения, стрелкой показано направление прихода волны). Кривая 1 относится к решетке, образованной 25 (5 на 5) элементами, кривая 2 – 225 (15 на 15) элементами.

Характерные максимумы, наблюдаемые на графиках, наличие которых позволило говорить об эффекте «прозрачности» объемных решеток, чередуются с не менее ярко выраженными минимумами. Это чередование указывает на интерференционный механизм, лежащий в основе вариаций уровня поля при изменении периода структуры либо длины волны.

Существенным является то, что характеристики решетки, изображенные на рис. 1, остаются практически неизменными для любого (не примыкающего к цилиндрам) положения точки наблюдения в пределах структуры. Т.е. можно утверждать, например, что условия относительного увеличения уровня поля, имеющего место в 225-элементной решетке вблизи центрального ее элемента при kd = 2,2, будут выполняться на всей протяженности структуры.

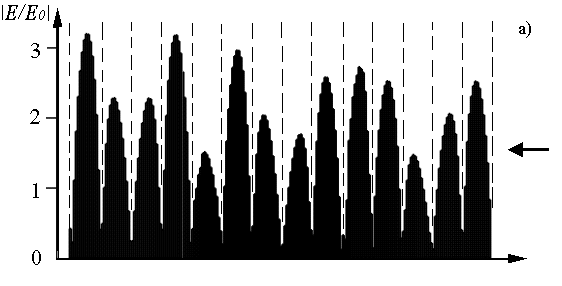
Подтверждением сказанного являются представленные на рис. 2 результаты расчета пространственного распределения поля в вышеуказанной решетке. Рис. 2а описывает распределение поля вдоль направления прихода падающей волны, рис. 2б – поперек. В обоих случаях точка наблюдения двигалась вдоль осей симметрии структуры, проходя при этом через ее центральный элемент. По оси ординат вновь отложена величина относительной напряженности поля в структуре, по оси абсцисс – расстояние. Стрелкой на рис. 2а показано направление прихода падающей волны, пунктирные линии на обоих рисунках описывают местоположение цилиндрических элементов. Расчет выполнялся таким образом, что в пределах одного периода уровень поля определялся в 15 равноудаленных друг от друга точках. Результаты расчета для удобства представлены в виде гистограммы, каждый элемент которой соответствует уровню поля в одной расчетной точке.

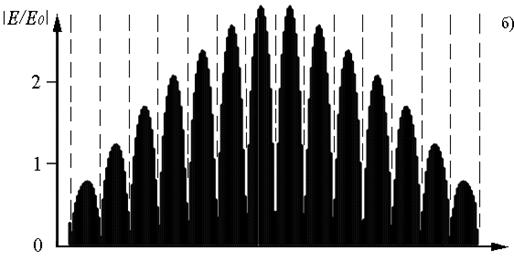
Рис. 2

Из рисунка следует, что превышение уровнем поля в решетке уровня поля в свободном пространстве действительно сохраняется в пределах всей структуры за исключением областей вблизи цилиндров.

Следует отметить, что наблюдающееся увеличение амплитуды поля внутри структуры не связано с притоком энергии извне решетки, поскольку имеет место и в неограниченной дискретной среде. Причина заключается в ее перераспределении в пределах структуры, а именно – при определенных периодах размещения элементов происходит отток энергии из областей, примыкающих к цилиндрам, в области, отдаленные от них (рис. 2).

Говоря о физике эффекта, можно предположить, что в формирование картины распределения поля основной вклад вносят элементы из ближнего окружения погруженной в структуру точки наблюдения, что подтверждается сходством характеристик простейших малоэлементных объемных решеток и весьма протяженных структур. Присутствие более удаленных элементов приводит лишь к увеличению изрезанности характеристик решеток, не меняя их принципиально (кривые 1 и 2 на рис. 1).

Если верно предположение о доминирующей роли ближайших к точке наблюдения элементов, следует допустить, что характеристика решетки формируется за счет эффектов однократного рассеяния волн на элементах структуры. Очевидно, что взаимным влиянием цилиндров, т.е. эффектами двух- и более кратного рассеяния, в случае малых поперечных размеров и небольшого количества элементов в структуре можно пренебречь даже при достаточно близком расположении рассеивателей.

В частности, известно [4], что применительно к дискретной среде приближение однократного рассеяния может быть использовано, если оптический путь волны в среде , где n – концентрация рассеивателей, L - геометрическое расстояние, пройденное волной в среде, - поперечник рассеяния частицы. В нашем случае поперечник рассеяния бесконечно протяженного цилиндра может быть определен по формуле [5]:

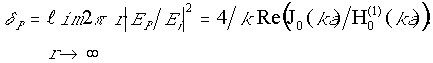
Здесь E_P и E_i – соответственно амплитуды рассеянной цилиндром и падающей на него волн.

Таким образом, для решетки, состоящей из цилиндров с вышеуказанными поперечными размерами, условие выполняется, если . Отсюда следует, что приближение однократного рассеяния может быть использовано для оценки характеристик, например, 25-элементной решетки, начиная со значений .

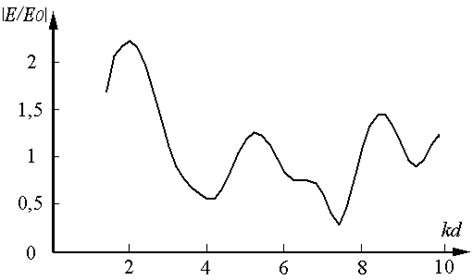
Доказательством этого могут служить изображенные на рис. 3 результаты расчета поля в структуре, аналогичной описанию рис. 1 (кривая 1), но выполненные в приближении однократного рассеяния (приближение Борна). Из сравнения рисунков видна полная аналогия характеристик структуры в обоих случаях, свидетельствующая о том, что распределение поля в рассматриваемой объемной решетке действительно определяется эффектами однократного рассеяния. В этом случае взаимодействие каждого элемента структуры с полем падающей волны можно рассматривать независимо от остальных рассеивателей в составе решетки.

Рис. 3

Проанализируем условия усиления полем, рассеянным на одиночном цилиндре, поля падающей волны. Для этого зафиксируем местоположение точки наблюдения и поместим около нее рассеиватель. Перемещая его относительно точки наблюдения, построим в плоскости, перпендикулярной оси цилиндра, области, располагаясь в которых, цилиндр будет усиливать поле падающей волны. Их конфигурация изображена на рис. 4 штриховкой. Указанные области чередуются с областями, при размещении в которых цилиндр будет ослаблять первичное поле. Положение точки наблюдения показано на рисунке точкой А.

Если около точки наблюдения разместить элементы двумерно-периодической структуры, то окажется, что при определенных параметрах решетки большая часть рассеивателей располагается либо в областях усиления, либо – ослабления, приводя тем самым соответственно к увеличению или уменьшению уровня поля в структуре относительно напряженности поля падающей волны. При изменении периода решетки эффекты усиления и ослабления чередуются между собой, что приводит к чередованию максимумов и минимумов на характеристике решетки (рис. 1). Необходимо отметить, что указанное чередование не периодично, поскольку геометрия изображенных на рис. 4 областей и рядов рассматриваемой структуры не совпадают.

Рис. 4

Если же при фиксированных параметрах решетки перемещать точку наблюдения, то наблюдаемое в пространстве чередование максимумов и минимумов поля станет строго периодическим, если речь идет о достаточно протяженной структуре, причем период повторения указанных экстремальных значений уровня поля будет совпадать с периодом решетки. При этом положение максимумов и минимумов поля в пределах элементарной ячейки структуры будет определяться, в основном, значениями этого периода. В частности, изображенная на рис. 2 картина описывает ситуацию, когда максимумы поля располагаются на равном удалении от соседних элементов решетки, а положение минимумов совпадает с положением элементов решетки, где поле минимально и в силу их идеальной проводимости. Такая ситуация и соответствует эффекту «прозрачности», т.е. превышению уровнем поля в решетке уровня поля в свободном пространстве на всем протяжении структуры за исключением областей, непосредственно примыкающих к цилиндрам.

При изменении периода структуры максимумы смещаются относительно цилиндров, «наплывают» на них, в результате чего распадаются на локальные максимумы меньшей амплитуды. При дальнейшем изменении периода возникает ситуация, обратная изображенной на рис. 2, когда максимумы поля совпадают с положением элементов решетки, а минимумы равноудалены от соседних цилиндров. В этом случае поле в пределах всей структуры оказывается значительно ослабленным.

Таким образом, доказано, что эффект «прозрачности» объемных двумерно-периодических решеток возникает вследствие интерференции падающей волны и волн, однократно рассеянных на элементах из ближайшей окрестности погруженной в структуру точки наблюдения. Определяющим возникновение эффекта параметром решетки является период расположения рассеивающих элементов. Отметим, что подобные эффекты, по-видимому, будут иметь место и в трехмерных регулярных структурах, состоящих, например, из сферических элементов.

СПИСОК ЛИТЕРАТУРЫ

1. Шестопалов В.П., Сиренко Ю.К. Динамическая теория решеток. Киев: Наукова думка, 1989.

2. Ветлужский А.Ю., Ломухин Ю.Л., Михайлова О.Г. Эффект прозрачности объемных решеток // РЭ. 1998. Т. 43. № 7. C. 797.

3. Ветлужский А.Ю., Ломухин Ю.Л Дифракция электромагнитных волн на двумерной системе периодически расположенных круговых цилиндров // РЭ. 2000. Т. 45. № 6. С.686.

4. Исимару А. Распространение и рассеяние волн в случайно-неоднородных средах. М.: Мир, 1981.

5. Иванов Е.И. Дифракция электромагнитных волн на двух телах. Минск: Наука и техника, 1968.

оглавление

дискуссия