|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6, 2002 |
|
Оптимизация стационарных ортогональных CDMA систем с прямым расширением спектра в условиях многолучевого распространения.
Архипкин В. Я. * ,
Иванов П. В. * ,
Смольянинов В. М. * ,
Сунь Лунцзе **.
* Kedah Electronics Engineering.
** Shaa’xi AETelecom Technology Co., LTD.
Получена 18 июня 2002 г.
Для стационарных ортогональных CDMA систем с прямым расширением спектра синтезированы оптимальные алгоритмы обработки в вариантах обобщенных эквалайзера и Rake-receiver, дано их сопоставление в алгоритмическом и реализационном планах. Получены простые соотношения для корреляционных связей помех в ветвях разнесения обобщенного Rake-receiver, на основе которых разработана процедура определения задержек в ветвях разнесения и контроля качества системы с использованием импульсного отклика, измеренного в канале пилот-сигнала. Приведены результаты моделирования прямой линии, подтвердившие работоспособность разработанных процедур и алгоритмов и продемонстрировавшие достижимое качество системы в двухлучевых и трехлучевых трассах.
I. Введение.
Применение
ортогональных расширяющих последовательностей в CDMA
системах с QPSK модуляцией в отдельных информационных
каналах в условиях однолучевого распространения и приемо-передающих трактов с
коэффициентом передачи типа поднятого косинуса позволяет практически идеально
разделить информационные каналы с пренебрежимо малым уровнем межканальных
помех. Требуемая для этого временная синхронность информационных каналов в
прямых радиолиниях выполняется автоматически, а в обратных – путем управления
задержкой излучаемых абонентскими станциями колебаний по командам, поступающим
с центральной станции. В отсутствие кодирования можно ожидать максимальный для
данной сигнально-кодовой конструкции скорости передачи информации, равной ![]() бит/с, где
бит/с, где ![]() – длительность
чипа расширяющей последовательности. При использовании кода со скоростью
– длительность
чипа расширяющей последовательности. При использовании кода со скоростью ![]() для коррекции
ошибок, возникающих за счет внешних помех, достижимая скорость будет равна
для коррекции
ошибок, возникающих за счет внешних помех, достижимая скорость будет равна ![]() бит/с.
бит/с.
При многолучевом распространении ортогональность сигналов, принадлежащих разным каналам, в прямых радиолиниях имеет место только в рамках отдельных лучей, а в обратных линиях – только в рамках главных лучей, по которым осуществляется сведение задержек. Наличие неортогональных компонент приводит к возникновению межканальных помех и снижению пропускной способности системы.
Известными
техническими средствами подавления межканальных помех является эквалайзер и Rake-receiver [1 ¸ 5]. Оптимизация эквалайзера
осуществляется либо по критерию минимального среднеквадратического искажения
чиповых отсчетов (почиповый эквалайзер [1]), либо по критерию минимального
среднеквадратического искажения битовых отсчетов (побитовый эквалайзер
[2]).
Оптимальный Rake-receiver
синтезируется по критерию минимума вероятности ошибочного приема [1, 3]. При
этом в случае CDMA системы межканальная помеха
аппроксимируется окрашенным гауссовским шумом [5]. Основными элементами как в
эквалайзере, так и в Rake-receiver
являются многоотводная линия задержки и устройство комбинирования с весовыми
коэффициентами, являющимися предметами поиска при оптимизации устройств. В
первоначальном варианте [1, 3] отводы в линиях задержки брались равноотстоящими
с интервалом, равным ![]() для CDMA систем.
При этом весовые коэффициенты в Rake-receiver
(называемым обычным) определяются только отсчетами импульсного отклика канала.
В [5] введен обобщенный Rake-receiver
с произвольным выбором задержек в ветвях разнесения с весовыми коэффициентами,
зависящими от корреляционных свойств помех. Показано, что обобщенный Rake-receiver по сравнению с обычным
может давать значительное преимущество при ограниченном числе ветвей
разнесения.
для CDMA систем.
При этом весовые коэффициенты в Rake-receiver
(называемым обычным) определяются только отсчетами импульсного отклика канала.
В [5] введен обобщенный Rake-receiver
с произвольным выбором задержек в ветвях разнесения с весовыми коэффициентами,
зависящими от корреляционных свойств помех. Показано, что обобщенный Rake-receiver по сравнению с обычным
может давать значительное преимущество при ограниченном числе ветвей
разнесения.
Представляется целесообразным сделать аналогичное обобщение и для эквалайзера, после чего осуществить сопоставление указанных средств борьбы с межканальной помехой. Полученные в [5] соотношения для обобщенного Rake-receiver из-за их сложности не могут быть использованы для этой цели.
Указанная в [5] возможность достижения большого положительного эффекта при ограниченном числе ветвей очень важна для практики, так как число ветвей определяет сложность устройства. Однако положительный эффект может быть получен лишь при правильном выборе задержек в ветвях разнесения. При этом ориентироваться можно только на измеренный с помощью пилот-сигнала импульсный отклик без решения задачи о числе лучей, которая в общем случае может не иметь однозначного решения. Для практики представляется чрезвычайно важной задача разработки процедуры выбора задержек в ветвях разнесения на основании измеренного импульсного отклика, а также оценка качества системы в зависимости от числа ветвей разнесения, позволяющая контролировать загрузку системы.
Таким образом, в настоящей работе ищется оптимальная процедура адаптации приемника к условиям распространения, описываемым импульсным откликом канала, который в общем случае не имеет ярко выраженной лучевой структуры. Адаптация осуществляется с учетом ограниченных технических возможностей, т.е. при фиксированном числе ветвей разнесения приемника не связанном с числом лучей, и состоит в оптимальном выборе задержек в ветвях разнесения и комплексных весовых коэффициентов в них. В статье разработаны алгоритмы, позволяющие на практике реализовать процедуру адаптации. Рассматриваются стационарные системы, для которых скорость изменения импульсного отклика мала и имеется возможность достаточно точно его измерить с использованием рандомизации расширяющих последовательностей. При сравнительном анализе качества функционирования алгоритмов обработки полагается импульсный отклик фиксированным, что представляется достаточным для выводов о их практической целесообразности. Реальный выигрыш разработанных алгоритмов на интервалах времени, превышающих постоянства отклика, может быть значительно выше оценок, полученных в статье.
II. Модель сигнала и помех в прямой линии.
Формируемые на
передающей стороне в n-ом информационном канале
дискретные отсчеты ![]() , следующие с чиповой частотой
, следующие с чиповой частотой ![]() с помощью
замены переменной
с помощью
замены переменной ![]() могут быть представлены в виде:
могут быть представлены в виде:
![]() , (1)
, (1)
где: ![]() – информационные
отсчеты в n-ом канале, следующие с частотой
– информационные
отсчеты в n-ом канале, следующие с частотой ![]() и принимающие
значения
и принимающие
значения ![]() :
:
![]() – расширяющая
последовательность в n-ом канале на i-ом
информационном периоде, принимающая также значения
– расширяющая
последовательность в n-ом канале на i-ом
информационном периоде, принимающая также значения ![]() . В совпадающем периоде
расширяющие последовательности для разных каналов ортогональны
. В совпадающем периоде
расширяющие последовательности для разных каналов ортогональны
На входе устройства цифровой обработки суммарный от всех информационных каналов сигнал может быть представлен в виде:
где: ![]() – сквозной отклик
тракта, включая передатчик, приемник и трассу;
– сквозной отклик
тракта, включая передатчик, приемник и трассу;
![]() – помеха, моделируемая
белым гауссовым шумом.
– помеха, моделируемая
белым гауссовым шумом.
После дискретизации имеем отсчеты
Рассмотрим обработку в одной ветви Rake-receiver в нулевом канале на нулевом периоде:
Уровень сигнальной
компоненты в рассматриваемой ветви равен ![]() . Остальные слагаемые в (5) представляют
собой помеховую компоненту
. Остальные слагаемые в (5) представляют
собой помеховую компоненту ![]() .
.
Она является
случайной в соответствии со случайностью информационных символов, помехи ![]() и используемой
рандомизацией.
и используемой
рандомизацией.
Для синтеза
алгоритма оптимального комбинирования выходов различных ветвей Rake-receiver необходимо знать
корреляционные связи помеховых компонент в ветвях с задержками ![]() и
и ![]() , т.е. функцию
, т.е. функцию
![]() .
.
С учетом рандомизации и независимости информационных отсчетов имеем
![]()
![]() .
.
Используя эти соотношения, не трудно получить
Важно отметить, что корреляционные связи не зависят ни от номера обрабатываемого канала, ни от номера периода, на котором осуществляется обработка, что является следствием использования рандомизации.
Формула (7)
отличается от полученных в работе [5] простотой и общностью с точки зрения
справедливости для любого импульсного отклика. Если импульсный отклик
суммарного тракта ![]() положить таким же, как в работе
[5], то
получим упрощенный вариант формул, имеющихся в работе [5]. Упростить формулы в
работе [5], имеющих вид трехмерных сумм, можно, объединив
положить таким же, как в работе
[5], то
получим упрощенный вариант формул, имеющихся в работе [5]. Упростить формулы в
работе [5], имеющих вид трехмерных сумм, можно, объединив ![]() и
и ![]() (формулы (25)
и (26) работы [5]) и осуществив суммирование по m при
фиксации суммарного сдвига
(формулы (25)
и (26) работы [5]) и осуществив суммирование по m при
фиксации суммарного сдвига ![]() .
.
Дальнейшее упрощение формулы (7) основано на использовании теоремы о выборках. Не трудно получить соотношение:
где:
Строгие
равенства в (8) и (8с) имеют место при строго полосовом колебании. Наличие
спектральных компонент за пределами полосы ![]() делает их приближенными.
делает их приближенными.
III. Модель сигнала и помех в обратной линии.
Полагается, что число абонентских станций (АС) в системе небольшое и обратные линии имеют достаточно большую информационную емкость так, что применение в них пилот-сигналов представляется вполне допустимым. С помощью пилот-сигналов можно оценить импульсные отклики в каждой обратной линии. Однако оценка осуществляется одновременно с функционированием цепей слежения, компенсирующих фазо-частотные и временные смещения, обусловленные расхождением опорных частот центральной и абонентской станций. При этом в межканальных помехах от других абонентских станций такой компенсации не происходит, что сказывается на свойствах суммарных помех.
Пусть имеется
Г обратных линий. Видеочастотный импульсный отклик в ![]() -ой линии
-ой линии ![]() с компенсируемым
цепью слежения фазочастотным набегом обозначим
с компенсируемым
цепью слежения фазочастотным набегом обозначим ![]() . Длительность откликов
. Длительность откликов ![]() полагается
меньшей половины длительности сигнала
полагается
меньшей половины длительности сигнала ![]() , что является необходимым условием
различимости сигналов, порождаемых соседними информационными символами.
Компенсация имеет место только в компонентах, относящихся к
, что является необходимым условием
различимости сигналов, порождаемых соседними информационными символами.
Компенсация имеет место только в компонентах, относящихся к ![]() -ой линии. В
компонентах, относящихся к другим линиям, полной компенсации не происходит
из-за расхождения опорных частот на АС. Расхождение частот будем полагать
небольшим так, что на интервале, равном одной длительности сигнала
-ой линии. В
компонентах, относящихся к другим линиям, полной компенсации не происходит
из-за расхождения опорных частот на АС. Расхождение частот будем полагать
небольшим так, что на интервале, равном одной длительности сигнала ![]() , относительный
набег фазы является незначительным, т.е.
, относительный
набег фазы является незначительным, т.е. ![]() , где
, где ![]() – разность частот АС на
центральной частоте
– разность частот АС на
центральной частоте ![]() . Соответствующее условие на относительную
неточность установки частот будет иметь вид
. Соответствующее условие на относительную
неточность установки частот будет иметь вид ![]() .
.
Рассмотрим
видеочастотный сигнал в канале приемника, выделяющего информацию, передаваемую
в r-ой обратной линии. Сигнальная компонента,
порождаемая r-ой линией, описывается откликом ![]() . Сигнальная
компонента, порождаемая g-ой
линией, описывается откликом
. Сигнальная
компонента, порождаемая g-ой
линией, описывается откликом ![]() , где
, где ![]() – фазовое смещение, обусловленное
расстройкой частот АС и постоянное на длительности сигнала при выполнении
указанных выше условий.
– фазовое смещение, обусловленное
расстройкой частот АС и постоянное на длительности сигнала при выполнении
указанных выше условий.
Расхождение опорных частот вызывает не только фазовые набеги, но и относительное временное расхождение импульсных откликов. За счет подстройки видеочастотных сеток частот эти расхождения будут медленными и можно полагать, что с помощью управления задержкой излучаемых колебаний достигается идеальное сведение задержек по главным лучам, обеспечивая ортогональность соответствующих этим лучам сигналов от разных станций.
После сделанных замечаний видеочастотное колебание в канале приемника, выделяющего информацию, передаваемую по r-ой обратной линии можно записать в виде:
где: ![]() –
множество номеров сигналов объемом
–
множество номеров сигналов объемом ![]() , используемых в g-ой обратной линии;
, используемых в g-ой обратной линии; ![]() – внешняя помеха типа белого гауссовского
шума. Выполняется условие
– внешняя помеха типа белого гауссовского
шума. Выполняется условие ![]() , где L –
общее число ортогональных сигналов (база).
, где L –
общее число ортогональных сигналов (база).
Дискретные отсчеты ![]() , следующие с
частотой
, следующие с
частотой ![]() ,
представляются в виде
,
представляются в виде
где: i
– номер информационного периода; ![]() – информационные отсчеты на i-ом периоде в n-ом информационном
канале g-ой линии;
– информационные отсчеты на i-ом периоде в n-ом информационном
канале g-ой линии; ![]() – расширяющие
последовательности ортогональные на i-ом периоде
для разных g и разных п в
пределах
– расширяющие
последовательности ортогональные на i-ом периоде
для разных g и разных п в
пределах ![]() .
.
Запись (9) верна для
интервала времени, соизмеримого с длительностью сигнала. Если ввести
зависимость от времени ![]() , то она действительна для интервалов, на
которых импульсные отклики
, то она действительна для интервалов, на
которых импульсные отклики ![]() не изменяются. Так как рассматриваются
стационарные системы, то эти интервалы являются достаточно большими, чтобы не
учитывать в (9) вариации
не изменяются. Так как рассматриваются
стационарные системы, то эти интервалы являются достаточно большими, чтобы не
учитывать в (9) вариации ![]() .
.
После дискретизации
на входе одной из ветвей Rake-receiver
будем иметь отсчеты ![]() , которые пропускаются через устройство
сжатия. На выходе устройства сжатия, соответствующего нулевому периоду (i = 0) и нулевому каналу (п = 0) r-ой обратной линии, будем иметь отсчеты:
, которые пропускаются через устройство
сжатия. На выходе устройства сжатия, соответствующего нулевому периоду (i = 0) и нулевому каналу (п = 0) r-ой обратной линии, будем иметь отсчеты:
где ![]() является сигнальной компонентой,
остальные – помеховой
является сигнальной компонентой,
остальные – помеховой ![]() , причем:
, причем:
составляющая, обусловленная белым гауссовским шумом;
составляющие межканальных помех, обусловленных g-ой обратной линией.
Корреляционные связи
помеховых компонент в ветвях с задержками ![]() и
и ![]() имеют вид:
имеют вид:
где для отдельных компонент выражения (13), используя результаты анализа прямой линии, можно получить:
где:
Следует отметить
важный факт, что неточность сведения опорных частот в указанных выше пределах,
не влияет на корреляционные связи межканальных помех и их оценка без учета
внешней помехи может быть осуществлена на основании измеряемых в цепях слежения
импульсных откликов ![]() . Более того, корреляционные связи помех не
зависят от номера r обратной линии, в которой
осуществляется извлечение информации, а также от номера п
обрабатываемого канала.
. Более того, корреляционные связи помех не
зависят от номера r обратной линии, в которой
осуществляется извлечение информации, а также от номера п
обрабатываемого канала.
IV. Алгоритмы оптимальной обработки в прямой радиолинии.
При синтезе
оптимального алгоритма функционирования Rake-receiver по критерию максимального правдоподобия исходным
является вектор-столбец ![]() отсчетов (5) на выходах устройств сжатия:
отсчетов (5) на выходах устройств сжатия:
где T – знак транспонирования.
В предположении гауссова закона распределения помеховых компонент решающая статистика имеет вид [6] скалярного произведения векторов
где ![]() – вектор-столбец весовых
коэффициентов, равный
– вектор-столбец весовых
коэффициентов, равный
где, в свою очередь: R-1 – матрица, обратная матрице R, состоящей из элементов ![]() (7); H – вектор-столбец, состоящий из элементов
(7); H – вектор-столбец, состоящий из элементов ![]() .
.
При синтезе оптимального обобщенного побитового эквалайзера, минимизирующего среднеквадратическое искажение канальных информационных отсчетов, исходными также являются отсчеты (15). Ищется весовой вектор Р, обеспечивающий
По структуре побитовый эквалайзер и Rake-receiver идентичны.
Поступая аналогично
[1], с учетом формул (5), (7) получаем для элементов ![]() вектора Р
систему линейных алгебраических уравнений:
вектора Р
систему линейных алгебраических уравнений:
или в матричном виде
Почиповый эквалайзер
рассмотрим в обобщенном виде. На его вход подаются вектор Х
отсчетов ![]() из
колебания (3), которое представим в виде:
из
колебания (3), которое представим в виде:
где дискретные отсчеты ![]() обладают
свойством:
обладают
свойством:
Почиповый эквалайзер
осуществляет весовую обработку ![]() , которая обеспечивает:
, которая обеспечивает:
Аналогично предыдущему можно
получить систему линейных алгебраических уравнений для элементов ![]() вектора V
вектора V
или в прежних обозначениях матриц и векторов имеем уравнение
Не трудно убедиться, что уравнения (20) и (25) имеют решения:
с коэффициентами ![]() и
и ![]() , которые можно
получить, подставив выражения (26а) и (26b) в
уравнения, соответственно, (20) и (25).
, которые можно
получить, подставив выражения (26а) и (26b) в
уравнения, соответственно, (20) и (25).
Таким образом, для всех критериев оптимальные алгоритмы совпадают с точностью до коэффициентов пропорциональности.
С точки зрения
технической реализации побитовый эквалайзер и Rake-receiver идентичны. В них весовое комбинирование
осуществляется с низкоскоростными отсчетами, следующим с частотой ![]() . В почиповом
эквалайзере комбинируются высокоскоростные отсчеты, следующие с частотой
. В почиповом
эквалайзере комбинируются высокоскоростные отсчеты, следующие с частотой ![]() . В Rake-receiver число устройств сжатия
на один информационный канал равно числу ветвей разнесения, в почиповом
эквалайзере требуется одно устройство сжатия на один информационный канал. При
числе ветвей разнесения М количество требуемых для комбинирования
операций (умножение – сложение) в почиповом эквалайзере на один сигнал
пропорционально ML, в Rake-receiver – пропорционально MN
на N информационных каналов. На устройство
сжатия в почиповом эквалайзере требуется LN
операций сложения (вычитания), а в Rake-receiver – MLN операций. Так
как операции комбинирования сложнее операций сложения – вычитания, то при N<L предпочтительнее
является структура Rake-receiver.
При
. В Rake-receiver число устройств сжатия
на один информационный канал равно числу ветвей разнесения, в почиповом
эквалайзере требуется одно устройство сжатия на один информационный канал. При
числе ветвей разнесения М количество требуемых для комбинирования
операций (умножение – сложение) в почиповом эквалайзере на один сигнал
пропорционально ML, в Rake-receiver – пропорционально MN
на N информационных каналов. На устройство
сжатия в почиповом эквалайзере требуется LN
операций сложения (вычитания), а в Rake-receiver – MLN операций. Так
как операции комбинирования сложнее операций сложения – вычитания, то при N<L предпочтительнее
является структура Rake-receiver.
При ![]() эквалайзер
может оказаться проще Rake-receiver.
Полная загрузка L=N
возникает лишь в редких случаях, поэтому среднее число вычислительных операций
в Rake-receiver будет меньше,
чем в почиповом эквалайзере.
эквалайзер
может оказаться проще Rake-receiver.
Полная загрузка L=N
возникает лишь в редких случаях, поэтому среднее число вычислительных операций
в Rake-receiver будет меньше,
чем в почиповом эквалайзере.
Для обратной линии можно получить аналогичные выражения для оптимальных алгоритмов с использованием соотношений (11) ¸ (14).
V. Процедура выбора задержек в ветвях разнесения Rake-receiver прямой радиолинии и контроля качества системы.
Сложность Rake-receiver определяется числом
ветвей разнесения. Естественным является стремление достичь при минимальной
сложности (числе ветвей) максимума положительного эффекта. Эта задача решается
путем выбора задержек в ветвях разнесения, максимизирующих отношение
сигнал/помеха на выходе Rake-receiver.
Ее строгое решение потребует исчерпывающих сведений об импульсном отклике
канала и корреляционных связей помех для всех возможных задержек. Получение
этих сведений потребует весьма сложной диагностической аппаратуры. Предлагаемые
здесь упрощенный алгоритм выбора задержек основан лишь на измерении импульсного
отклика канала ![]() с помощью пилот-сигнала.
с помощью пилот-сигнала.
Процедура использует выражение для отношения сигнал/помеха на выходе устройства оптимального комбинирования
в отсутствии внешней белой
гауссовой помехи, т.е. с использованием только измеренного импульсного отклика ![]() . В принципе,
задаваясь числом ветвей
. В принципе,
задаваясь числом ветвей ![]() и варьируя в них задержками, можно
попытаться найти максимум этого отношения. Однако практически эта процедура
вряд ли реализуема, так как функция (27) зависит от
и варьируя в них задержками, можно
попытаться найти максимум этого отношения. Однако практически эта процедура
вряд ли реализуема, так как функция (27) зависит от ![]() параметров. Поэтому
предлагается пошаговая процедура определения задержек, когда для нахождения
задержки в
параметров. Поэтому
предлагается пошаговая процедура определения задержек, когда для нахождения
задержки в ![]() -ой
ветви используются найденные на предыдущих этапах задержки в
-ой
ветви используются найденные на предыдущих этапах задержки в ![]() ветвях. При
этом будет оптимизироваться одномерная функция (27), что в реализационном плане
не представляет особых сложностей. Более того, процедура построена так, что на
каждом шаге в выражении (27) фигурируют двумерные матрицы
ветвях. При
этом будет оптимизироваться одномерная функция (27), что в реализационном плане
не представляет особых сложностей. Более того, процедура построена так, что на
каждом шаге в выражении (27) фигурируют двумерные матрицы ![]() и
и ![]() , что также упрощает
вычислительную процедуру.
, что также упрощает
вычислительную процедуру.
На начальном этапе
задержки первых ветвей находятся с помощью поиска максимумов ![]() . Если имеется
несколько максимумов одинакового уровня, разнесенных по задержке более чем на
. Если имеется
несколько максимумов одинакового уровня, разнесенных по задержке более чем на ![]() , то
представляется целесообразным использовать в качестве исходных все найденные
эквивалентные задержки. Объединим все эти ветви в одну, используя оптимальные
веса. Для эквивалентных задержек веса по модулю будут одинаковыми.
, то
представляется целесообразным использовать в качестве исходных все найденные
эквивалентные задержки. Объединим все эти ветви в одну, используя оптимальные
веса. Для эквивалентных задержек веса по модулю будут одинаковыми.
Пусть найдены
задержки ![]() для
для
![]() ветвей
и найдены в соответствии с (17) оптимальные коэффициенты
ветвей
и найдены в соответствии с (17) оптимальные коэффициенты ![]() их комбинирования.
Объединим эти ветви в одну, рассматривая на ее выходе величину
их комбинирования.
Объединим эти ветви в одну, рассматривая на ее выходе величину
Сигнальная компонента на выходе комбинированной ветви без учета информационного символа
помеховая компонента
Ее дисперсия
где (см. 8):
Ищем задержку для ![]() -ой ветви.
Сигнальная компонента в ней
-ой ветви.
Сигнальная компонента в ней
![]() ,
,
а дисперсия помеховой
Взаимная корреляция помех в
комбинированной и в ![]() -ой ветви
-ой ветви
Рассматриваем оптимальное комбинирование этих двух ветвей в соответствии с (16) и (17). При этом для отношения сигнал/помеха в соответствии с (27) получаем
Эта величина является функцией
одного переменного ![]() . Определив расчетным путем максимум этой
функции с использованием соотношений (29) – (33), находим задержку для
. Определив расчетным путем максимум этой
функции с использованием соотношений (29) – (33), находим задержку для ![]() -ой ветви.
-ой ветви.
Замечаем, что
двумерный вектор весовых коэффициентов, обеспечивающий максимум (34), в
сочетании с весовыми коэффициентами ![]() в общем случае не обеспечивает оптимальных
весовых коэффициентов в задаче комбинирования
в общем случае не обеспечивает оптимальных
весовых коэффициентов в задаче комбинирования ![]() ветвей с заданными задержками.
Поэтому после определения задержки
ветвей с заданными задержками.
Поэтому после определения задержки ![]()
![]() -ой ветви необходимо вычислить оптимальные
весовые коэффициенты для комбинирования
-ой ветви необходимо вычислить оптимальные
весовые коэффициенты для комбинирования ![]() ветвей, используя выражения (17) и (8).
При этом, естественно, итоговая величина
ветвей, используя выражения (17) и (8).
При этом, естественно, итоговая величина ![]() будет не меньше, чем найденный максимум
отношения (34).
будет не меньше, чем найденный максимум
отношения (34).
Описанная процедура продолжается до тех пор, пока либо не будут найдены задержки для всех имеющихся в резерве ветвей разнесения, либо при меньшем числе ветвей разнесения вычисляемое на каждом шаге отношение сигнал/помеха не достигнет некоторого порогового значения, зависящего от уровня внешней помехи и определяемого в процессе моделирования устройства обработки. Достигаемое отношение сигнал/помеха зависит от загрузки системы и ее сравнение с порогом позволяет контролировать загрузку и управлять ею с изменением условий распространения.
Аналогично строится процедура выбора задержек в обобщенном Rake-receiver обратных линий.
VI. Результаты моделирования Rake-receiver в прямой линии.
Блок-схема модели изображена на рис.1. Модель реализована в математической среде MATLAB.
На вход подаются
чиповые отсчеты ![]() , равные сумме чиповых отсчетов отдельных
информационных каналов, формируемых в I и Q квадратуре, и пилот-сигнала в I
квадратуре. ПСП различных каналов в отдельной квадратуре – ортогональны с базой
, равные сумме чиповых отсчетов отдельных
информационных каналов, формируемых в I и Q квадратуре, и пилот-сигнала в I
квадратуре. ПСП различных каналов в отдельной квадратуре – ортогональны с базой
![]() . В
каждой квадратуре передавалось по 64 канала со случайными независимыми
информационными отсчетами, т.е. информационная загрузка составляла половину
максимально возможной. С целью выравнивания вероятностных характеристик каналов
использовался способ рандомизации, описанный в [7] и основанный на перестановке
номеров ПСП с периодом в 128 сигналов.
. В
каждой квадратуре передавалось по 64 канала со случайными независимыми
информационными отсчетами, т.е. информационная загрузка составляла половину
максимально возможной. С целью выравнивания вероятностных характеристик каналов
использовался способ рандомизации, описанный в [7] и основанный на перестановке
номеров ПСП с периодом в 128 сигналов.
Отсчеты ![]() пропускались
через фильтр с амплитудно-частотной характеристикой, равной корню квадратному
из поднятого косинуса. Коэффициент прямоугольности равен 0,22. Отсчеты на
выходе фильтра формировались с частотой
пропускались
через фильтр с амплитудно-частотной характеристикой, равной корню квадратному
из поднятого косинуса. Коэффициент прямоугольности равен 0,22. Отсчеты на
выходе фильтра формировались с частотой ![]() и далее подавались на модель многолучевой
трассы.
и далее подавались на модель многолучевой
трассы.
Многолучевая трасса
имитировалась многоотводной линией задержки с возможной вариацией задержек с
дискретом ![]() .
Амплитуды и фазы лучей определяются множителями
.
Амплитуды и фазы лучей определяются множителями ![]() на отводах линии задержки.
на отводах линии задержки.
К сформированным отсчетам сигналов добавлялись независимые отсчеты белого гауссовского шума, имитирующие внешнюю помеху.
Смесь сигнала и помехи подавалась на фильтр с амплитудно-частотной характеристикой, равной корню квадратному из поднятого косинуса, имитирующего входной фильтр приемника.
В блоке оценок обрабатывается пилот-сигнал с целью получения следующих оценок:
1.
Оценивается импульсный отклик ![]() канала с временем усреднения 1280 периодов
сигналов.
канала с временем усреднения 1280 периодов
сигналов.
2. По описанному пошаговому алгоритму оцениваются задержки в ветвях разнесения Rake-receiver.
3. Для определенных задержек оценивается корреляционная матрица помеховых компонент в ветвях разнесения Rake-receiver. Время усреднения составляет 1280 периодов сигналов.
4. Оцениваются весовые коэффициенты для комбинирования выходов ветвей Rake-receiver при различном числе ветвей разнесения.
Rake-receiver функционирован в двух
режимах. В обычном с числом ветвей разнесения от одного до числа лучей в канале
с весовыми коэффициентами, комплексно-сопряженными отсчетам импульсного
отклика. Задержки считались известными и равными задержкам в модели канала. При
разностях задержек в лучах более ![]() такой подход близок к реальному
функционированию, заключающемся в поиске
такой подход близок к реальному
функционированию, заключающемся в поиске ![]() . При сближении по задержке лучей этот
подход не отражает реального поведения. В обобщенном режиме задержки в ветвях и
коэффициенты комбинирования брались из блока оценок. Результатом моделирования
явились зависимости отношения сигнал / помеха от числа ветвей
разнесения. При оценке отношения сигнал / помеха усреднение
производилось по всем информационным в I и Q квадратуре каналам. Время усреднения – 128 периодов
сигнала, соответственно общее число независимых отсчетов
. При сближении по задержке лучей этот
подход не отражает реального поведения. В обобщенном режиме задержки в ветвях и
коэффициенты комбинирования брались из блока оценок. Результатом моделирования
явились зависимости отношения сигнал / помеха от числа ветвей
разнесения. При оценке отношения сигнал / помеха усреднение
производилось по всем информационным в I и Q квадратуре каналам. Время усреднения – 128 периодов
сигнала, соответственно общее число независимых отсчетов ![]() .
.
Одним из параметров,
влияющим на указанные выше зависимости, является уровень внешних помех, который
определялся через заданное отношение энергии канального сигнала ![]() к спектральной
плотности помех
к спектральной
плотности помех ![]() . При этом энергия сигнала вычислялась как
сумма энергий отдельных лучей. Отношение
. При этом энергия сигнала вычислялась как
сумма энергий отдельных лучей. Отношение ![]() принималось равным 10 и 15 дБ, а также в
качестве предельного, характеризующего качество функционирования в отсутствии
внешних помех, полагалось
принималось равным 10 и 15 дБ, а также в
качестве предельного, характеризующего качество функционирования в отсутствии
внешних помех, полагалось ![]() дБ.
дБ.
Моделирование осуществлялось для двухлучевых и трехлучевых трасс со случайными задержками и фазами сигналов в лучах. Амплитуды сигналов в лучах полагались одинаковыми, что является наихудшим случаем по уровню межканальных помех.
Легко осуществить
теоретический анализ отношения сигнал/помеха в обычном Rake-receiver, когда задержки сигналов в лучах отличаются более
чем на ![]() и
коррелированностью помех можно пренебречь. При этом выигрыш обычного Rake-receiver при равных амплитудах
по сравнению с приемом по одной ветви составляет
и
коррелированностью помех можно пренебречь. При этом выигрыш обычного Rake-receiver при равных амплитудах
по сравнению с приемом по одной ветви составляет ![]() дБ, где М – число лучей. В
процессе моделирования были обнаружены случаи, когда этот выигрыш не
достигался. К ним относятся ситуации, когда задержки отличаются менее, чем на
дБ, где М – число лучей. В
процессе моделирования были обнаружены случаи, когда этот выигрыш не
достигался. К ним относятся ситуации, когда задержки отличаются менее, чем на ![]() , а также в
трехлучевой трассе при равноотстоящих по задержке лучах. Эти ситуации
моделировались отдельно. При этом случайными были начальные фазы сигналов в
лучах. Объем статистики составлял до 60-ти сеансов со случайным выбором
параметров, входящих в каждую ситуацию.
, а также в
трехлучевой трассе при равноотстоящих по задержке лучах. Эти ситуации
моделировались отдельно. При этом случайными были начальные фазы сигналов в
лучах. Объем статистики составлял до 60-ти сеансов со случайным выбором
параметров, входящих в каждую ситуацию.
По результатам моделирования сделаны следующие основные выводы:
1.
Обычный Rake-receiver с
числом ветвей разнесения, равным числу лучей М, выигрывает по сравнению
с приемом по одной ветви до ![]() дБ. Однако в особых ситуациях, отмеченных
выше, этот выигрыш снижается до 1 дБ в трехлучевой трассе.
дБ. Однако в особых ситуациях, отмеченных
выше, этот выигрыш снижается до 1 дБ в трехлучевой трассе.
2.
Обобщенный Rake-receiver
с числом ветвей разнесения, равным числу лучей М, выигрывает по
сравнению с обычным Rake-receiver
от 0 до 4,6 дБ. При числе ветвей разнесения до 6-ти выигрыш обобщенного Rake-receiver по сравнению с обычным
составляет от 2,5 дБ и выше. При этом обобщенный Rake-receiver эффективно функционирует даже при
близкорасположенных по задержке лучах. Так при двух лучах с противофазными
сигналами и взаимной задержкой 0,6 ![]() и 4-х ветвях разнесения выигрыш по
сравнению с приемом по одной ветви составляет 2,3 дБ при
и 4-х ветвях разнесения выигрыш по
сравнению с приемом по одной ветви составляет 2,3 дБ при ![]() дБ и 3,5 дБ при
дБ и 3,5 дБ при ![]() дБ. Т.е.
применение обобщенного Rake-receiver
эквивалентно некоторому увеличению разрешающей способности сигналов,
определяемой длительностью чипа
дБ. Т.е.
применение обобщенного Rake-receiver
эквивалентно некоторому увеличению разрешающей способности сигналов,
определяемой длительностью чипа ![]() .
.
3.
Обобщенный Rake-receiver
при числе ветвей разнесения до 6-ти во всех моделируемых ситуациях обеспечивает
заданное качество передачи информации (вероятность ошибочного приема на бит ![]() ) при пороговом
отношении кодека
) при пороговом
отношении кодека ![]() дБ, имеющего скорость
дБ, имеющего скорость ![]() , и половинной загрузке
системы. Обычный Rake-receiver
обеспечивает заданное качество при числе загрузочных каналов в 2 ¸ 3 раза меньше.
, и половинной загрузке
системы. Обычный Rake-receiver
обеспечивает заданное качество при числе загрузочных каналов в 2 ¸ 3 раза меньше.
4.
Для ![]() дБ
найдено пороговое значение 9 дБ, с которым необходимо сравнивать вычисляемое
отношение
дБ
найдено пороговое значение 9 дБ, с которым необходимо сравнивать вычисляемое
отношение ![]() в
пошаговой процедуре определения задержек в ветвях разнесения. Этот порог
гарантирует выходное значение отношения энергии
в
пошаговой процедуре определения задержек в ветвях разнесения. Этот порог
гарантирует выходное значение отношения энергии ![]() , приходящейся на один бит
передаваемой информации, к эквивалентной спектральной плотности
, приходящейся на один бит
передаваемой информации, к эквивалентной спектральной плотности ![]() не менее 5 дБ.
Для
не менее 5 дБ.
Для ![]() дБ
гарантированное значение
дБ
гарантированное значение ![]() составляет 7 дБ. Более чем в 50% случаев
при числе ветвей разнесения до 6-ти указанные пороговые значения были
превышены, что свидетельствует о возможности повышения загрузки системы по
сравнению с заложенной при моделировании.
составляет 7 дБ. Более чем в 50% случаев
при числе ветвей разнесения до 6-ти указанные пороговые значения были
превышены, что свидетельствует о возможности повышения загрузки системы по
сравнению с заложенной при моделировании.
VII. Заключение.
Таким образом, в настоящей работе показана алгоритмическая эквивалентность оптимальных обобщенных эквалайзера и Rake-receiver. По среднему числу вычислительных операций реализация в варианте Rake-receiver, как правило, экономичнее эквалайзера.
Получены достаточно простые соотношения, описывающие корреляционные связи помех в ветвях разнесения Rake-receiver при произвольном выборе задержек в них. С использованием этих соотношений разработана процедура выбора близких к оптимальным задержек в ветвях на основе измеренного в канале пилот-сигнала импульсного отклика трассы. Процедура не предполагает анализа импульсного отклика на предмет определения характера многолучевости.
Установлено
пороговое значение для вычисляемого в разработанной процедуре отношения ![]() , позволяющего
контролировать и управлять загрузкой системы. Пороговое значение не зависит от
характеристик многолучевых трасс.
, позволяющего
контролировать и управлять загрузкой системы. Пороговое значение не зависит от
характеристик многолучевых трасс.
Моделирование
процедуры и алгоритмов обработки показало высокую эффективность обобщенного Rake-receiver по сравнению с обычным
и со случаем приема по одной ветви. В двух- и трехлучевых трассах при числе
ветвей разнесения до 6-ти может быть достигнута половинная загрузка системы при
кодеке со скоростью ![]() и пороговом значении
и пороговом значении ![]() дБ. С помощью указанного
выше контроля во многих случаях загрузка может быть увеличена. С обычным Rake-receiver пропускная способность
в 2 ¸ 3 раза ниже указанной.
дБ. С помощью указанного
выше контроля во многих случаях загрузка может быть увеличена. С обычным Rake-receiver пропускная способность
в 2 ¸ 3 раза ниже указанной.
Несмотря на то, что работа сориентирована на стационарные системы, ее результаты могут быть применены и для прямых линий мобильных CDMA систем связи.
VIII. Литература.
1. Proakis J.G. Digital communication. - McGraw-Hill, New York, 1995.ns, 1995.
2. Mirbagheri A., Yoon Y.C. Performance comparision of linear MMSE and coherent Rake receivers in multipath asynchronous random – CDMA // Spread Spectrum Techniques and Applications, 2000 IEEE Sixth International Symposium, Vol.2, 2000, Page(s): 520-524.
3. Price R. and Green P.E. A Communication Technique for Multipath Channels // Proc.IRE, Vol.46, pp. 555-570, March.
4. D.L.Noneaker, Optimal combining for Rake reception in mobile cellular CDMA forward links // Proc. IEEE Military Commun. Conf., Bedford, MA, 1998.
5. Bottomley G.E., Ottosson T., Wang Y.-P.E. A Generalized Rake receiver for Interference Suppression // Selected Areas in Communications, IEEE J., Vol.18, Issue: 8, August.
6. Ширман Я.Д. Радиоэлектронные системы. Основы построения и теория. Справочник. Москва ЗАО “МАКВИС”, 1998.
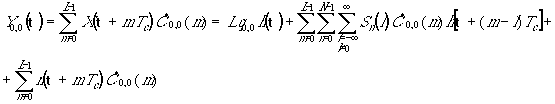 (5)
(5)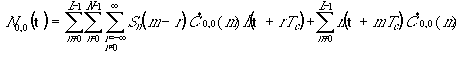 (6)
(6) (7)
(7)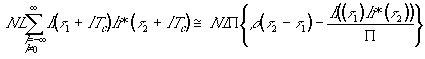 (8)
(8) (12
(12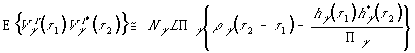 (14а)
(14а)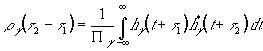
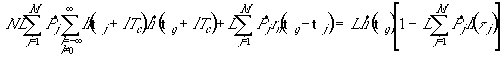 , (
, (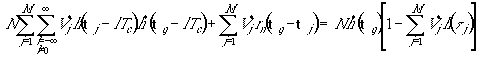 , (
, (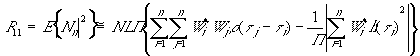 , (31)
, (31)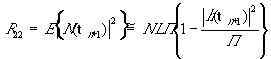 . (32)
. (32) . (34)
. (34)